俯仰角速度对弹丸侵彻多层靶弹道影响

程 伟，熊国松，李伟兵，张振雷，张学伦

（1. 重庆红宇精密工业集团有限公司，重庆 402760；2. 南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094）

1 引言

弹丸作用于指挥所、通信大楼等楼房类目标时具有行程长、弹道不稳定等特点，俯仰角速度在导弹飞行、弹靶交会等状态下广泛存在，是影响侵彻多层靶的弹道稳定性重要因素之一。为确保弹丸能够准确命中典型建筑物并在其内部爆轰，有必要对其弹道稳定性进行研究。

国内外关于弹道稳定性的研究大多针对钢筋混凝土强度靶开展，对于侵彻多层靶的弹道稳定性研究较少。1978 年AVSD 等［1］采用流体动力学程序对弹丸攻角和倾角引起的弹道偏转效应进行计算分析。1996 年M.J. Forrestal 等［2］在经典空腔膨胀理论的基础上进行修正，对弹丸侵彻过程进行研究。2010 年P.K. Jena 等［3］通过试验方法研究了攻角效应对侵彻过程的影响。2013 年李金柱等［4］开展了弹丸斜侵彻有限厚混凝土靶板试验，研究了弹丸的剩余速度、贯穿靶板后的姿态角与初始倾角的关系。2016 年马兆芳等［5］开展了弹丸侵彻多层间隔混凝土靶的试验和数值模拟，研究了攻角和尾裙角度对弹道稳定性的影响。2018 年J. Feng 等［6］研究了撞击速度对弹坑的影响。由于弹丸侵彻多层靶试验时的初始条件不是完全可控，导致研究费用高、周期长、随机性大，因此，开展弹丸侵彻多层靶弹道的数值模拟研究，确定部分影响因素对弹丸侵彻多层钢筋混凝土靶弹道的影响规律，指导弹丸方案设计和导弹总体设计非常有意义。

为此，本研究开展了弹丸侵彻多层钢筋混凝土靶试验和数值模拟，通过对比分析考虑与不考虑俯仰角速度影响下弹丸侵彻弹道，得到了俯仰角速度对弹丸侵彻多层钢筋混凝土靶弹道的影响规律，获取了弹丸不偏离典型目标建筑物的临界俯仰角速度范围。

2 弹丸侵彻多层钢筋混凝土靶试验

研究开展了弹丸侵彻八层钢筋混凝土薄靶试验，预置初始条件为着速750 m·s-1、着角15°、攻角3°，试验初始条件根据高速摄像机判读为着速735 m·s-1、着角15°、攻角-1.7°。试验后回收弹丸如图1 所示，其下部漆面未直接接触靶标保存较为完整。钢筋混凝土薄靶发生了基于微裂纹的混凝土拉伸加载响应，即拉伸波作用下的脆性断裂和压缩加载下的挤压破碎［5］，典型靶标破坏结果如图2 所示。

图1 弹丸侵彻钢筋混凝土薄靶试验中弹丸漆面破坏效果Fig.1 Damage of the paint surface of projectile penetrating into multi⁃layered targe

图2 典型靶标破坏结果Fig.2 Results of the destruction of a typical target

本试验的试验弹道如图3 所示，研究中设置弹道向下偏移为负，向上偏移为正，设置左面第一块靶板为第1 层，右面第一块靶板为第8 层。由图3 可以看出，试验弹道曲线向下偏移，前四层偏移较小，弹丸姿态变化也较小，后四层偏移逐渐增大，且弹丸姿态变化也增大。

图3 弹丸侵彻8 层钢筋混凝土薄靶试验的试验弹道图Fig.3 Experimental results of ballistic trajectory of projectile in the experiment of projectile penetrating 8⁃layer reinforced concrete target

弹丸攻角从3°变为-1.7°的飞行过程中，形成了初始俯仰角速度，其主要由着靶前的姿态变化引发，如图4 所示，其计算公式如式（1）：

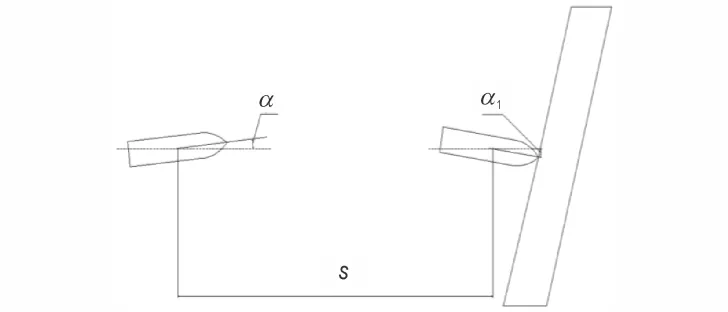
图4 俯仰角速度形成示意图Fig.4 Schematic diagram of the pitch angular velocity

式中，ω为俯仰角速度，顺时针为正，逆时针为负［7］，（°·s-1）；α为弹丸预置攻角，（°）；α1为各种因素综合作用下的着靶攻角，（°）；s为着靶阶段的飞行距离，m；v为着靶阶段的平均飞行速度，m·s-1。本试验中α=3°，α1=-1.7°，s=8.09 m，v=735 m·s-1，带入式（1）可得ω=427°·s-1。

弹丸侵彻过程受力示意如图5 所示。初始正俯仰角速度和负攻角同时作用会增大弹丸的俯仰角速度，从而增大攻角。增大的攻角使得弹丸横向受力面积大幅增加，使得弹丸的俯仰角速度和攻角越来越大，受力状况也越来越恶劣，进一步导致侵彻弹道发生变化。

图5 弹丸侵彻过程受力示意图Fig.5 Schematic diagram of the force analysis during the projectile penetration

3 弹丸侵彻多层钢筋混凝土靶弹道数值模拟

在分析大量文献基础上，采用LS⁃DYNA 有限元软件，开展弹丸侵彻多层钢筋混凝土靶弹道数值模拟研究，对比分析考虑与不考虑俯仰角速度对着靶时间、着靶速度、着靶点偏移、攻角、着角、引信过载等参数的影响，为俯仰角速度对弹丸侵彻弹道的影响规律研究奠定基础。

3.1 弹丸侵彻多层钢筋混凝土靶数值模拟方法

研究开展了弹丸侵彻多层钢筋混凝土靶数值模拟，采用Lagrange 算法［8-9］，单位制为cm、g、μs。建立二分之一数值模拟模型，其中弹丸头部为尖卵形，头部CRH 曲线为3，长径比为5，外形、质心、转动惯量等弹体参数与试验相同，靶标厚度、靶间距、靶板倾角等靶板参数与试验一致，具体如图6a 所示。靶标网格在对称面附近有5 倍弹径的加密区，如图6b 所示。弹靶作用区域弹丸和多层钢筋混凝土靶的网格比例约为3∶2，如图6c 所示，划分原则参照文献［10］。混凝土靶板网格尺寸由弹丸半径和网格边长的比值λ来确定，为得到规则的过载曲线、符合实际的损伤区形等理想计算结果，λ取6.0。

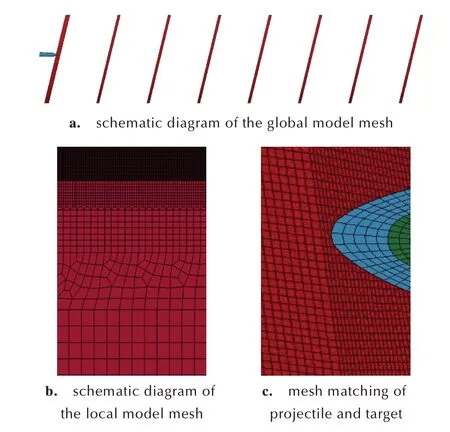
图6 整体和局部网格图Fig.6 Schematic diagram of the global and local model mesh

钢筋混凝土靶标采取分离方法建模，钢筋采用BEAM 单元描述，混凝土采用SOLID 164 单元描述。在钢筋混凝土穿甲的数值模拟［11］的基础上，改进了钢筋和混凝土采用耦合算法，采用CONSTRAID_BEAM_IN_SOLID_PENALTY 关键字进行耦合控制，其优点在于考虑了动能守恒，能较好地模拟钢筋在混凝土中的拖拽现象。由于弹丸材料为高强度合金钢，在侵彻过程中几乎不存在质量侵蚀和变形，采用线弹性塑性硬化模型。对钢筋，采用理想弹塑性模型。材料参数如表1 所示。

表1 弹丸、钢筋材料模型参数Table 1 Parameters of the projectile and the reinforcement

混凝土连续损伤Taylor⁃Chen⁃Kuszmaul［12-13］模型是将混凝土的破坏响应模型通过微裂纹连续损伤原理来建立，可较好地描述混凝土动态断裂过程包括微裂纹的成核、扩展、聚合和碎片形成，材料参数如表2所示。

表2 混凝土材料模型参数Table 2 Parameters of the concrete

3.2 不考虑俯仰角速度影响的数值模拟结果分析

采用上述弹丸侵彻多层钢筋混凝土靶数值模拟方法，开展不考虑俯仰角速度影响下的试验与数值模拟结果对比分析。数值模拟获取的弹丸速度曲线如图7所示，与试验对比如表3 所示。由于试验靶后存在弹长范围内弹丸被混凝土块覆盖不利于判读速度的问题，对比以靶前速度进行，速度误差计算公式为：

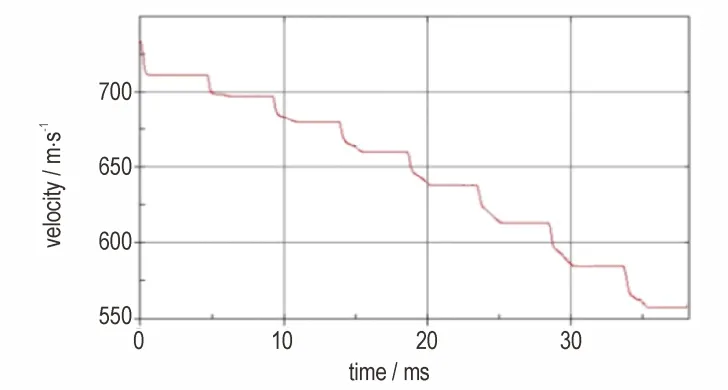
图7 弹丸速度时间曲线Fig.7 Velocity⁃time curve of the projectile

式中，δ为误差；vexp为试验靶前速度，m·s-1；vsimulated为数值模拟靶前速度，m·s-1。

由表3 可知，第2～8 层靶前速度试验与数值模拟结果对比误差小于2.5%，最大误差不超过15 m·s-1。因此可认为就侵彻能力而言，上述数值模拟方法是可行的。

表3 靶前速度的模拟与实验对比Table 3 Comparison of landing velocity between the experi⁃mental and the simulation

图8 为不考虑俯仰角速度影响的数值模拟弹道示意图。根据图3 和图8 可知，试验和数值模拟弹道偏转趋势、弹道曲线基本一致，均向下偏移，具体偏移量为表4。由表4 可以看出，前5 层靶的着靶点偏移量试验与数值模拟对比误差较小，6～8 层逐渐增大，第8 层误差达54 cm，导致了弹丸侵彻姿态与试验有较大差别，不能较好的为弹丸结构强度分析提供支撑。

图8 不考虑俯仰角速度影响下弹丸弹道数值模拟结果Fig.8 Simulation of the penetration trajectory without con⁃sidering the effect of pitch angular velocity

表4 弹道偏移量对比表Table 4 Offset comparison between the experimental and the simulation

3.3 考虑俯仰角速度影响的数值模拟结果分析

在不考虑俯仰角速度影响的数值模拟方法基础上，引入试验中实际存在的俯仰角速度开展考虑俯仰角速度影响的数值模拟结果分析。LS⁃DYNA 程序中使用关键字*INITIAL_VELOCITY_GENERATION加载俯仰角速度，由角速度大小、基准点坐标、方向共同实现，俯仰角速度作用在质心上。考虑俯仰角速度影响的数值模拟侵彻弹道如图9 所示。根据图3、图9 和表4 形成考虑俯仰角速度影响的着靶时间t、着靶速度v1、着靶点偏移d、攻角β、着角α等定量数据试验与数值模拟对比表，具体如表5 所示。显然，根据图10 和表5 可知，考虑俯仰角速度条件下数值模拟弹道与试验现象更符合，第8 层最大偏差为14 cm，较不考虑俯仰角速度条件下第8 层弹道偏差54 cm 缩小40 cm。

图9 考虑俯仰角速度影响的弹丸弹道数值模拟结果Fig.9 Simulation of penetration trajectory with considering the effect of pitch angular velocity

通过表5 分析可得：1）每层着靶时间误差不大于1000 μs，误差最大为3.5%；2）每层着靶速度最大差值为15 m·s-1，误差最大为2.5%；3）每层弹孔偏移量最大差值约为14 cm，呈逐渐增大的趋势；4）着角逐渐逼近0°，弹道逐渐偏转，试验与数值模拟最大误差与1.4°；5）攻角逐渐变大，给弹丸结构强度带来负面影响。误差存在的主要原因是数值模拟环境较试验更为理想、试验数据测量误差、钢筋混凝土靶标的离散性等。

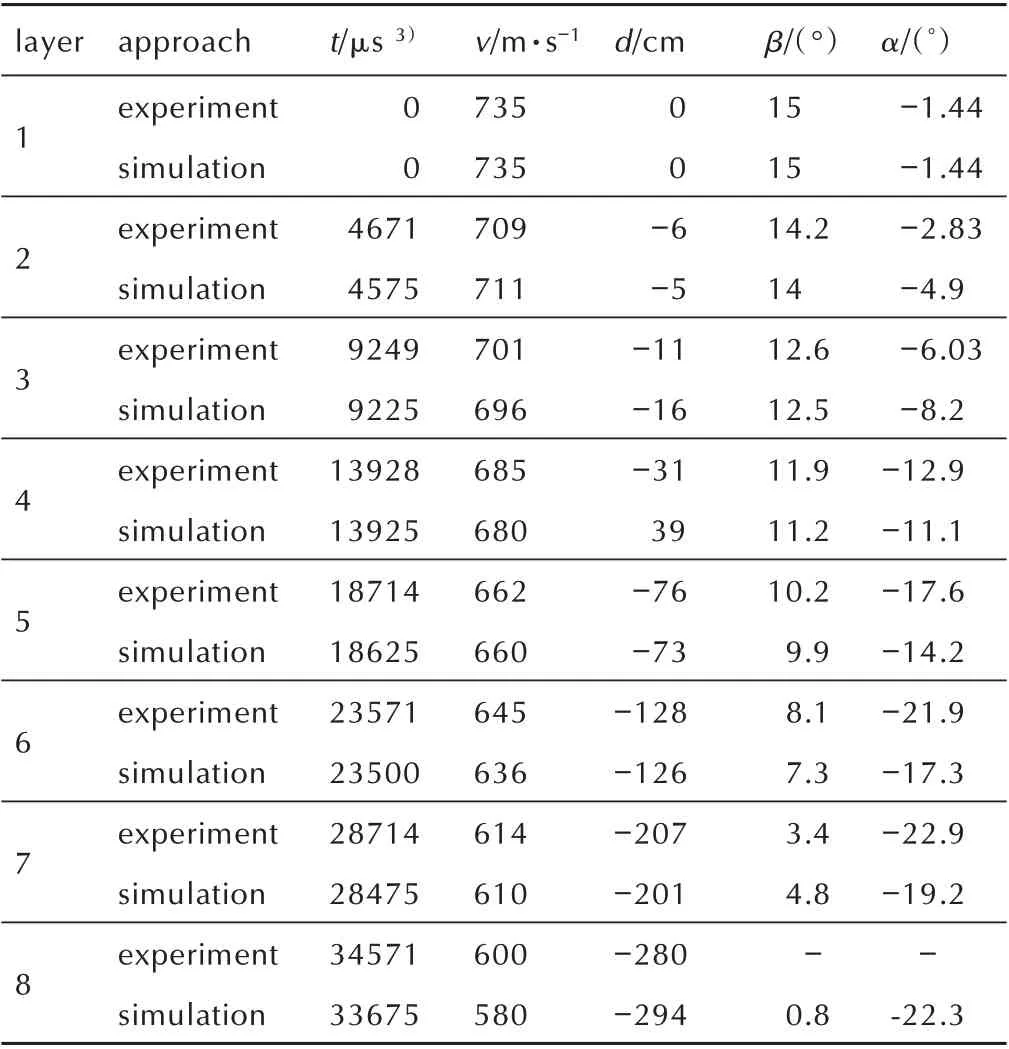
表5 考虑俯仰角速度影响的数值模拟与试验数据对比表Table 5 Comparison of theresults of the experimental and the simulation with considering the pitch angular velocity

通过本研究中试验时搭载引信测得的弹丸侵彻钢筋混凝土靶过载时间曲线如图10 所示，弹丸侵层钢筋混凝土靶过载时间计算曲线以D3plot 文件输出时间与引信频率对应以及同平面多点平均的方法提取，所得结果如图11 所示。通过分析试验与数值模拟数据可得：1）引信横向加速度最高峰值约为50000 g，均在第一层出现；2）负向过载越来越大，第6 层达到峰值约42000 g；3）过载峰值间隔时间约4900 ms，试验与数值模拟基本一致。

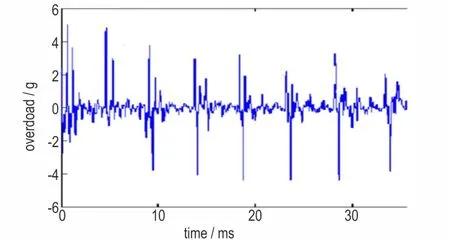
图10 引信过载时间实测曲线Fig.10 Overloading⁃time curve of fuse in experiment

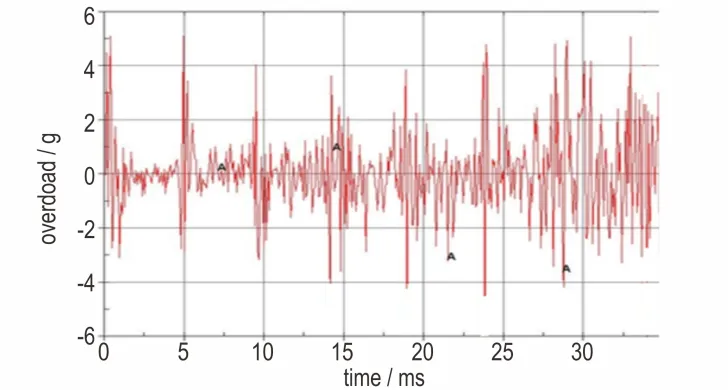
图11 引信过载时间计算曲线Fig.11 Overloading⁃time curve of the fuse in simulation

在考虑着靶速度、攻角、着角等常规初始条件之外引入俯仰角速度后，第8 层偏差为由54 cm 降低为14 cm，试验与数值模拟的弹道更吻合，且过载时间曲线一致性也较好，可以满足侵彻多层钢筋混凝土靶弹丸方案能力预测与优选。

4 俯仰角速度对弹丸侵彻多层钢筋混凝土靶弹道的影响规律

4.1 不同俯仰角速度对弹丸弹道的影响

为进行俯仰角速度对弹丸侵彻多层钢筋混凝土靶弹道的影响规律研究，采用考虑俯仰角速度的数值模拟方法开展了本研究中试验相同大小但反方向俯仰角速度-427°·s-1为初始条件的弹丸侵彻多层靶分析，并与俯仰角速度为0、427°·s-1时的数值模拟弹道进行对比。图12 为-427°·s-1时弹丸轨迹数值模拟示意图。

图12 -427°·s-1俯仰角速度影响下弹丸弹道数值模拟结果Fig.12 Simulation results of projectile trajectory at the pitch angular velocity of -472°·s-1

由图5、图6、图13 对比分析可以看出，俯仰角速度的改变可明显改变弹丸的侵彻弹道。当俯仰角速度由427°·s-1逐步变为-427°·s-1时，弹丸的弹道由向下偏转逐步改变为向上偏转，弹道趋势完全相反。俯仰角分别为-427°·s-1、0°·s-1、427°·s-1条件下的弹道对比如图13 所示。

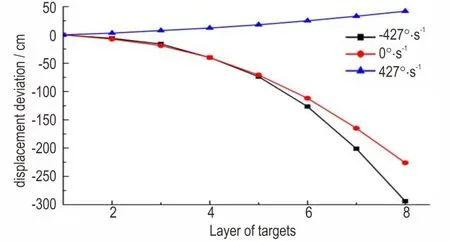
图13 不同俯仰角速度下弹丸的弹道偏移量对比图Fig.13 Comparison of the trajectory offset of projectile with three different pitch angular velocities

由图13 可以看出，俯仰角速度为0°·s-1和427°·s-1时，前5 层弹道区别不大，后3 层偏移量偏差迅速增大，且总体偏移量在第八层都在220 cm 以上。俯仰角速度为-427°·s-1时，总体偏移量仅为42 cm，远小于俯仰角速度为0°·s-1和427°·s-1时的偏移量。

4.2 临界俯仰角速度数值模拟研究

由于上述典型目标幅面为600 cm*600 cm，一般认为偏移量超过300 cm 弹丸就不能完全发挥其毁伤效能。因此，为了保证此类弹丸能在目标内部作用，完全发挥其毁伤效能，需考虑控制弹丸俯仰角速度以降低俯仰角速度对弹丸侵彻多层混凝土靶弹道的影响。

由图13 和表6 可知当俯仰角速度为427°·s-1时，弹丸侵彻第8 层靶时已经撞击在靶标下边缘，偏移量达到294 cm。根据图13 所示数值模拟结果，每次减少100°·s-1进行数值模拟分析，当俯仰角速度为-627°·s-1时，弹丸侵彻第8 层靶时已经撞击在靶标上边缘，如图14 和图15 所示。因此，为确保本研究弹丸其侵彻弹道的纵向偏移量在300 cm 以内，可认为俯仰角速度为427°·s-1和-627°·s-1是此弹丸能在目标内部作用的极限值。

图14 -627°·s-1俯仰角速度影响下弹丸轨迹数值模拟结果Fig.14 Simulation results of projectile trajectory at the pitch angular velocity of -627°·s-1

图15 确保弹丸能在目标内部作用的负俯仰角速度影响图Fig.15 Diagram of the influence of negative pith angular ve⁃locity to ensure the projectile acting inside the target

5 结论

开展了考虑/不考虑俯仰角速度条件下弹丸侵彻多层靶数值模拟，研究了弹丸侵彻多层靶的过程，基于试验验证结果，分析了俯仰角速度对弹丸侵彻多层钢筋混凝土靶弹道的影响，所得结论如下：

1）在考虑着靶速度、攻角、着角等常规初始条件之外引入俯仰角速度，开展弹丸侵彻多层钢筋混凝土靶数值模拟，获取弹丸侵彻多层靶的着靶时间、着靶速度、着靶点偏移、攻角、着角、引信过载等定量数据并与试验对比，考虑俯仰角速度与试验更吻合。

2）俯仰角速度方向对弹丸侵彻多层钢筋混凝土弹道影响明显，俯仰角速度由427°·s-1逐渐变化为负427°·s-1时，弹丸的弹道从向下偏转转变为向上偏转，由于着靶时有15°着角的原因导致了同等大小情况负向俯仰角速度比正向俯仰角速度对弹道影响更大。

3）开展俯仰角速度对侵彻弹道的影响规律研究，为确保本文弹丸能在目标内部作用，其侵彻弹道的纵向偏移量在300 cm 以内，弹丸着靶时的临界俯仰角速度为-627°·s-1～427°·s-1之间。