炸药装药爆炸反应演化过程和约束影响的数值模拟
楼建锋,张树道
(北京应用物理与计算数学研究所,北京 100094)
1 引言
炸药装药在遭遇高速破片、射流打击或雷管引爆等情况,较强冲击波进入炸药后,因材料超快速压缩而激活基体中大量微介观热点产生反应放能,使加载冲击波不断增强,在亚微秒或数微秒时间、毫米特征尺度上快速转化为稳定传播的爆轰波。
相比较而言,炸药在遭遇意外事故而引发局部点火燃烧问题,由于冲击强度相对较低,一般情况都无法形成冲击波、不会直接激活炸药基体内部热点而导致冲击起爆,通常是绝热剪切、界面摩擦等非冲击点火机制引起局部能量沉积导致炸药表面升温点火、燃烧[1⁃2]。燃烧反应初期压力增长比较缓慢,在百微秒或毫秒时间达到百兆帕,如果装药壳体约束较强,密闭空间中压力不断增强,反应会向高烈度方向发展,引发不同程度的爆炸响应,装药内不同部位的压力可以达到数百兆帕、甚至千兆帕量级。而如果壳体约束较弱,压力达到一定程度会导致壳体破裂解体、压力骤降,反应可能会因泄压而熄灭,或在约束解除后转为常压下持续燃烧。
近年来,国内外学者针对非冲击条件下炸药燃烧反应开展了很多研究工作[3-10],认识了裂纹传播、燃烧模式转换对于反应演化的重要性。例如,Jack⁃son 等[6]采用质子辐射照相直接观测烤燃实验,尚海林等[9]使用高速摄影观测压装炸药间隙中燃烧产物对流传播和烈度演化的物理行为特征,李涛等[10]通过约束球形装药中心点火实验观测高烈度反应条件下燃烧裂纹传播过程。然而大部分工作仅依赖于实验表象观测或于典型位置超压测量,难以精密诊断炸药内部网状裂纹分形/分叉动态扩展过程,还不能清楚认识炸药反应机制转变过程。理论和数值模拟研究方面,由于炸药裂纹动态扩展与燃烧反应耦合过程很难表征,反应烈度转变与装药结构、约束强度等因素非线性耦合,缺乏用于描述炸药反应增长过程的模型和参数,目前能对炸药内部动态裂纹扩展和燃烧反应进行耦合计算的算法程序并不多见。
因此,本研究围绕弱刺激条件下装药局部点火后,缓慢燃烧反应向剧烈爆炸演化的复杂过程,开展了炸药爆炸反应过程的力学建模和数值模拟方法研究。基于多介质任意拉式欧拉方法和流固耦合技术,实现了局部点火后反应增长及其与壳体相互作用的数值模拟。构建了炸药爆炸反应速率增长的唯像模型,通过对不同约束结构内炸药反应压力增长过程的数值模拟,分析了装药约束对爆炸反应演化的影响。
2 研究方法
2.1 流固耦合数值模拟方法
研究弱刺激条件下装药局部点火、反应增长及其爆炸效应问题,由于炸药反应气态产物的流动性很大,用Lagrangian 算法计算爆炸反应过程会遇到大变形的困难,一般使用Euler 算法计算,但是Euler方法在计算过程中网格固定不动,网格之间物理量的输运存在数值耗散,不能清晰描述物质界面。为了能够处理流体大变形以及精确跟踪物质界面,通常采用任意拉式欧拉耦合算法(Arbitrary Lagrangian⁃Eulerian,简称ALE),并采用重分重映技术来处理大变形和物质界面问题。然而对于炸药爆炸反应问题,还会出现混合网格,即一个网格内同时包含未反应炸药和反应产物等物质,因此,本研究选用了多介质任意拉式欧拉算法(Multi⁃material Arbi⁃trary Lagrangian⁃Eulerian,简称MMALE)[11]。该方法允许存在混合网格,利用物质界面重构方式来替代网格重分,允许物质界面跨过网格,是模拟多介质大变形流动的有效手段。
为了较好地描述爆炸驱动壳体结构的膨胀破坏过程,壳体结构采用Lagrangian 算法。气态产物与壳体结构之间的相互作用,采用流固耦合(Fluid⁃Structure Interaction)算法处理[12-13],气态产物给壳体结构施加载荷,而壳体结构相当于边界条件约束气态产物的运动。本研究通过LS⁃DYNA 软件中流固耦合技术的应用开发,实现装药炸药爆炸反应及其与壳体结构相互作用问题的数值模拟。
2.2 爆炸反应演化增长唯像模型
为了描述装药局部点火后缓慢燃烧反应到剧烈爆炸反应的演化过程,构建了炸药爆炸反应速率增长的唯像模型。基于缝隙燃烧实验[8-9]、强约束球形装药中心点火实验[10]结果分析,认识了炸药反应演化的主导机制和压力增长特征。假定反应速率与燃烧面面积和压力相关,并且将点火后炸药反应演化分为缓慢反应和剧烈反应两个过程,由此构建了两项式反应速率增长唯像模型如式(1)所示。
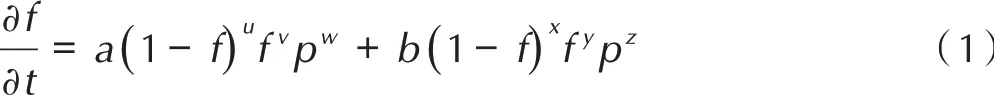
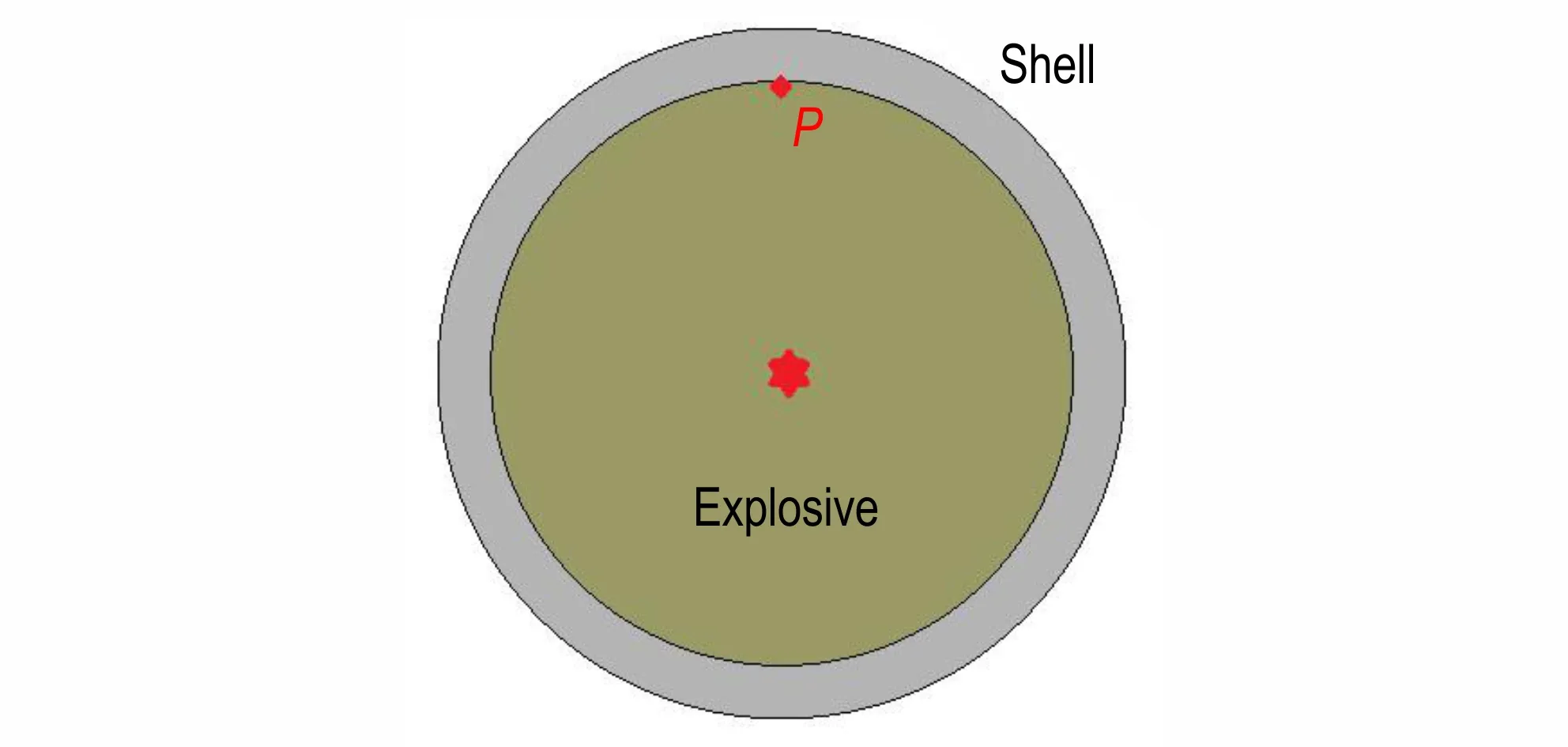
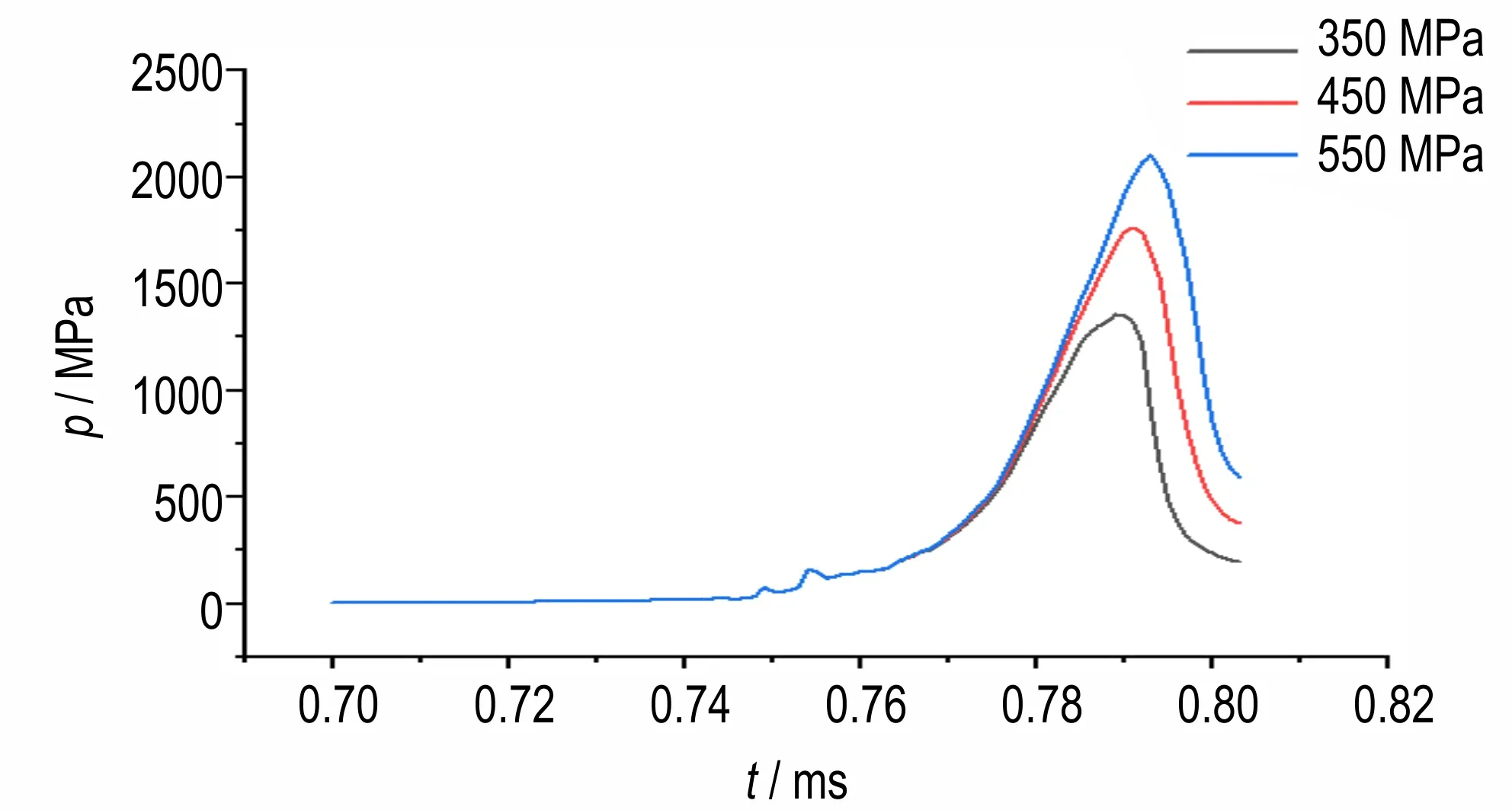
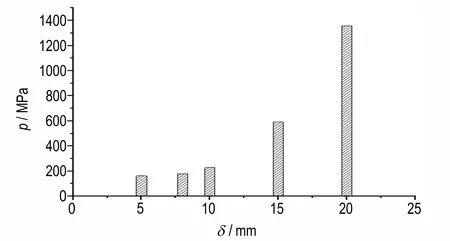
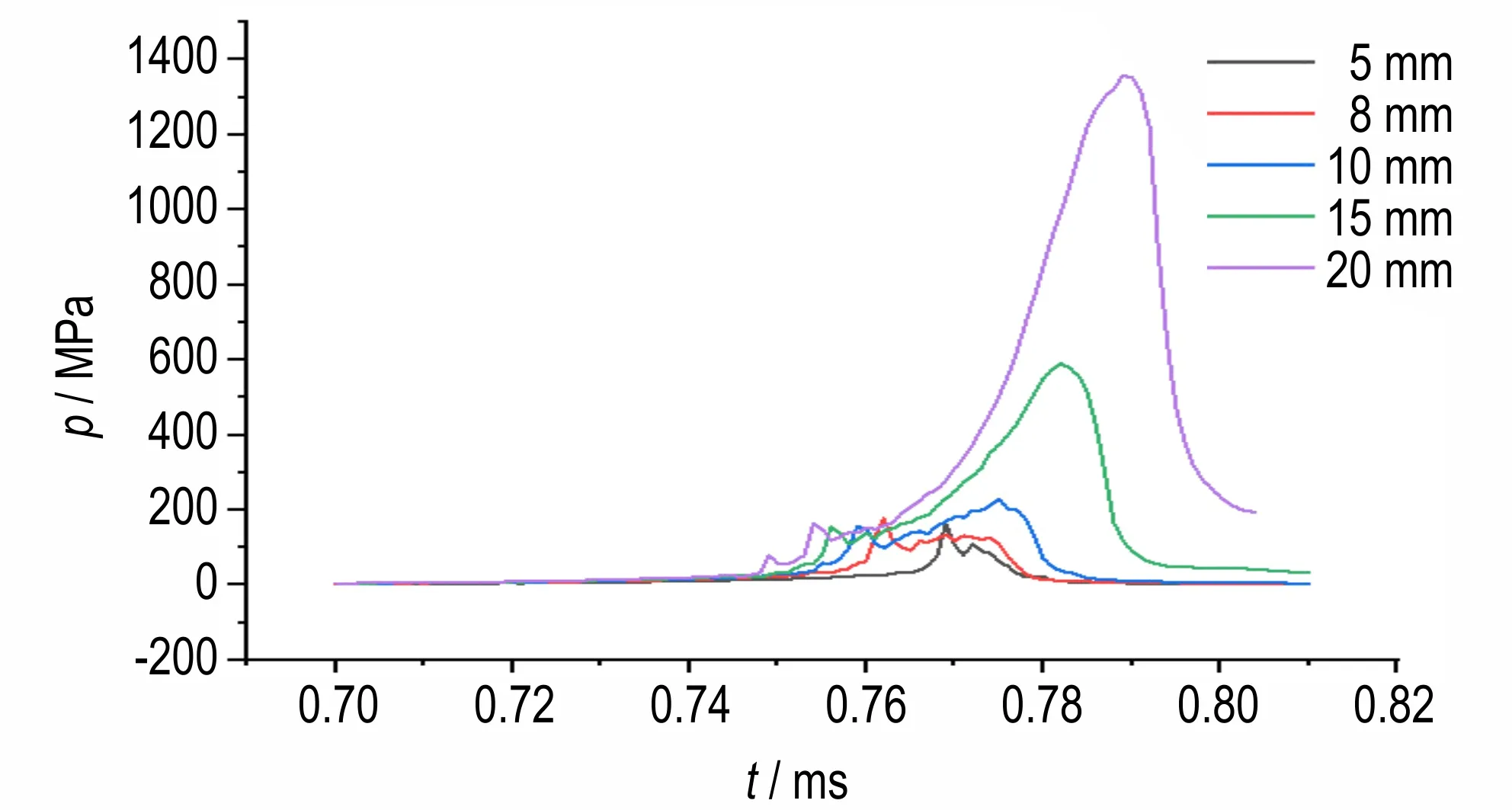
式中,f是化学反应进程(f= 0 表示没有反应,f= 1 表示完全反应);t是时间,μs;p是压力,GPa;a、b、u、v、w、x、y和z是待定系数。a(1-f)ufvpw和b(1-f)xfypz分别表示缓慢反应和剧烈反应,其中(1-f)ufv和(1-f)xfy用于近似描述反应速率和燃烧面面积的相关性。反应初期,即0 图1 爆炸与爆轰反应增压过程对比示意图Fig.1 Comparison of pressure⁃increasing between explosion and detonation 未反应炸药及气态产物的压力都采用JWL 形式的状态方程进行描述, 式中,A、B、R1、R2、ω为实验拟合参数;CV为比热,GPa·K-1;T是温度,K;V=ρ0/ρ,ρ为密度,g·cm-3,ρ0为初始密度,g·cm-3。 为了分析装药局部点火后炸药反应演化增长及其与壳体相互作用问题,基于强约束球形装药中心点火实验[10]开展了计算建模和数值模拟。 本研究对文献[10]中全钢结构约束实验进行了简化建模,约束结构简化成20 mm 厚的钢壳,炸药球直径为110 mm,材料是压装PBX⁃2 炸药(HMX 含量为95%),密度是1.86 g·cm-3,用1 g 黑火药在炸药中心进行点火(见图2)。钢壳本构模型采用理想弹塑性模型,钢壳密度是7.85 g·cm-3,屈服强度是350 MPa,钢壳失效断裂判据采用最大主应力和等效塑性应变的组合形式。计算模型中,网格单元的尺寸是0.5 mm。 通过药球中心点火后爆炸反应演化过程的数值模拟,获得了典型位置的压力变化历史曲线,以及反应压力波在药球中传播和驱动外壳膨胀破坏过程的数值模拟图像。基于炸药与壳体交界面的P点(见图2)压力变化曲线的实验结果[10],进行了爆炸反应速率模型关键参数的选取和优化。根据压力变化曲线从缓慢增加转变到迅速增大阶段的拐点,确定了临界反应进程(取值为0.012),主要参数如表1 所示,其中未反应炸药及气态产物状态方程的参数参考文献[15-16],如表2所示。 图2 强约束球形装药中心点火实验示意图Fig.2 Configuration of spherical charge under strong con⁃finement 表1 PBX⁃2 炸药爆炸反应增长唯像模型的主要参数Table 1 Parameters of the Reaction Growth Model for PBX⁃2 表2 PBX⁃2 炸药的状态方程参数Table 2 Equation of state parameters for PBX⁃2 图3 显示了典型位置P点压力增长历史曲线的数值模拟结果与实验结果的对比情况。可以看到,炸药反应压力增加过程大致可以分为三个阶段,早期阶段Ⅰ压力增加非常缓慢,经过数百微秒,压力才达到200 MPa,随后出现迅速增长,在阶段Ⅱ中,经过20~40 μs,压力超过1 GPa,但是随着外壳膨胀破裂产生泄压作用,压力并没有继续增加,反而迅速降低(阶段Ш)。据此验证了流固耦合数值模拟方法在计算炸药爆炸反应及后效问题的适用性和有效性。 图3 P 点处压力随时间变化曲线与实验结果对比Fig.3 Comparison of pressure versus time curve at point P with experimental result 图4 是反应压力波在药球中演化传播及其驱动外壳膨胀和破坏过程的数值模拟图像,各图中显示典型时刻的压力。图4a 和图4b 表示炸药中心点火后早期缓慢反应阶段,大约经过500 μs 炸药压力超过200 MPa;图4c 和图4d 是压力波在药球中演化传播的过程,压力波到达外壳后发生反射,压力增大并加剧炸药反应,同时驱动外壳膨胀;图4e 是发生剧烈反应迅速增压后,约束壳体被爆炸波破坏的图像;图4f 是外壳破裂泄压阶段的图像。 图4 反应压力波在药球中传播及驱动外壳膨胀破坏过程的数值模拟图像Fig.4 Images of pressure wave propagating in explosive ball and driving shell expansion 为了分析装药约束对反应压力增长过程的影响,在上述计算模型的基础上,设计了两类计算模型:一类是改变外壳约束的强度,另一类是改变外壳约束的厚度。分别开展了中心点火后爆炸反应压力增长过程的一系列数值模拟。 为了考察外壳约束强度对反应压力增长的影响,针对钢壳厚度是20 mm 的情况,设计计算模型钢壳材料的屈服强度分别是350,450 MPa 和550 MPa,开展了数值模拟。图5 显示了装药典型位置P点处炸药压力变化过程的对比情况,相对应的压力峰值分别是1357,1763 MPa 和2104 MPa。可以看到,对于20 mm 厚度三种不同钢壳强度的模型,压力变化曲线都是包含缓慢增加、迅速增长和降低等过程,即炸药经历了缓慢反应到剧烈爆炸的过程,而随着壳体强度的增加,典型位置炸药压力峰值也增大,表明了约束强度对炸药反应向高烈度演化的促进作用。 图5 不同约束强度,P 点处压力随时间变化曲线Fig.5 Comparison of pressure versus time curves at point P for different shell strength 考虑武器弹药装药壳体的厚度范围,设计了五个计算模型,将钢壳厚度分别设置为5,8,10,15 mm 和20 mm,通过数值模拟得到装药典型位置P点的炸药反应压力增长曲线。图6 显示了五个模型装药典型位置压力峰值的对比情况,横坐标δ是壳体厚度,可以看到,随着钢壳厚度从5 mm 增加到20 mm,压力峰值逐渐增大,从163 MPa 增大到1357 MPa,即钢壳厚度对压力增长过程存在较大的影响。图7 显示了典型位置炸药压力增长曲线的对比情况,在外壳厚度较薄(5,8 mm 和10 mm)时,炸药压力增长比较缓慢,没有出现迅速增长过程(即阶段Ⅱ)外壳就发生膨胀和破裂,产生泄压;而外壳厚度为15 mm 和20 mm 的情况,都进入了压力迅速增长阶段,而且压力峰值也骤然增加,引发炸药剧烈爆炸反应,但是随着壳体膨胀和破坏解体,抑制了剧烈爆炸向爆轰反应的转变,并没有达到爆轰的状态[8]。 图6 不同约束厚度下,P 点处压力峰值的对比图Fig.6 Comparison of maximum pressure at point P for differ⁃ent shell thickness 图7 不同约束厚度下,P 点处压力随时间变化曲线Fig.7 Comparison of pressure versus time curves at point P for different shell thickness (1)基于多介质任意拉式欧拉方法(MMALE)和流固耦合技术,实现了弱刺激条件下装药局部点火、反应增长及其爆炸效应的数值模拟。 (2)针对炸药装药从缓慢燃烧反应到剧烈爆炸的演化过程,构建了炸药爆炸反应演化增长的唯像模型,数值模拟了强约束球形装药中心点火实验,标定了主要的模型参数。 (3)约束条件对炸药爆炸反应压力增长过程的影响研究结果表明,壳体强度或厚度增加,装药内反应压力的峰值也增大;随着钢壳厚度从5 mm 增加到20 mm,压力峰值从163 MPa 增大到1357 MPa,但是压力增长过程的差异很大。薄壳装药内压力增长缓慢,可能没有出现剧烈反应,就发生壳体破裂泄压;而对于厚壳约束,可能发生剧烈爆炸,但随着壳体的破裂解体,抑制了剧烈爆炸向爆轰反应的转变。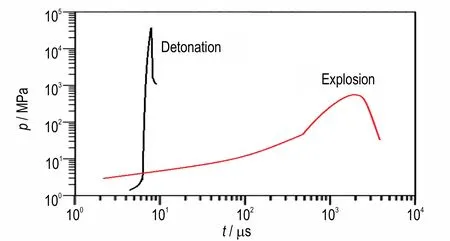
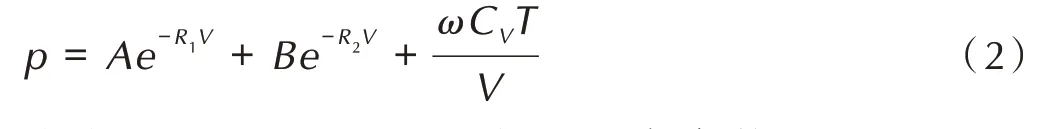
3 炸药爆炸反应演化过程的数值模拟

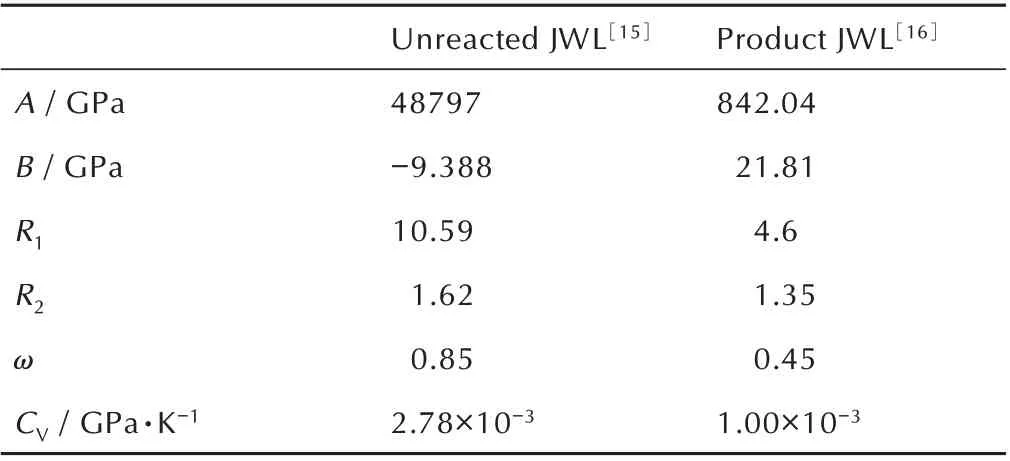
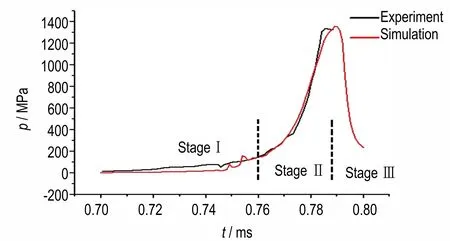
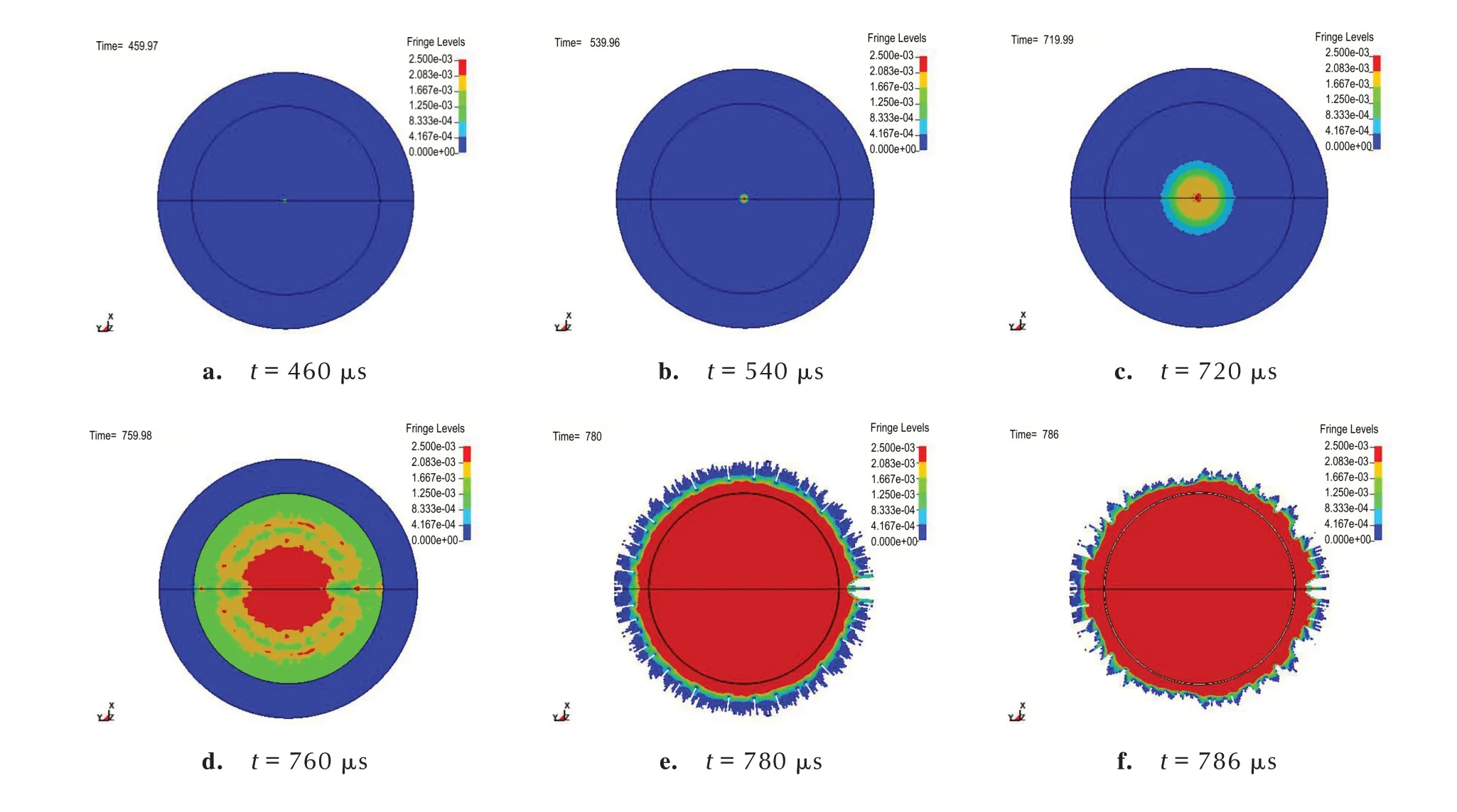
4 装药约束对反应压力增长过程的影响
4.1 不同约束强度对反应压力增长的影响
4.2 不同约束厚度对反应压力增长的影响
5 结论

