分层PageRank算法和逆序系数在铁路网络中的应用
刘芝秀,熊 可,黄小杰*
(1.南昌工程学院理学院,江西 南昌 330099;2.江西财经大学统计学院,江西 南昌 330077)
铁路交通是最为重要的公共基础设施之一,是社会经济发展的重要支撑。随着我国铁路和高铁建设的不断推进,其建设规模与技术都取得了巨大的成就,国内各个城市和区域之间的交通往来更为便利。通常经济发达的地方其城际铁路交通也较发达,显然各城市列车站点的重要性是一个值得探讨的问题,至少有助于分析铁路网络的安全性与效能。关于城市网络结点重要性的计算,文献[1]提出了一种适应PageRank算法,此算法考虑了来源数据本身的重要程度,使城市网络中来自相邻结点的数据比来自较远结点的数据更有可能被考虑,并据此计算每个城市结点的重要性。
其中PageRank方法最初是用于评价互联网上网站的知名度和重要性,它是由Page及其同事于1998年提出的[2]。经过不断的发展和改进,PageRank方法已被广泛的应用于社会生活的各个方面,例如近期的文献[3]将其应用于挖掘各学科的优秀和潜在人才,文献[4]将其用于对负责生物状态动态变化的转录因子进行排序,文献[5]采用PageRank方法识别了光伏并网系统中的关键线路,文献[6]将PageRank方法应用于分析陕西省COVID-19患者动态接触网络,文献[7]也基于PageRank算法对号称全球贸易先行“晴雨表”的中间品贸易的关键节点进行了识别和分析。一般的,如果所研究的事物能够用网络连接图模型来描述,PageRank方法就有其潜在的应用价值,而城市间的铁路交通网络正是一个典型的网络连接图,本文基于这一事实,并考虑到我国直辖和省会城市在城市群中的特殊地位,而提出了便于并行计算的分层PageRank算法,结合各城市铁路站点间往返列车班次数据,将其用于计算各城市铁路站点的重要性及排名;为说明所计算的PageRank值能够体现城市列车站点的重要性,本文还将城市列车站点的PageRank排名与2020年城市GDP排名进行了比较,比较过程中引入了逆序系数的概念,逆序系数越大,两种排序差异越大,而逆序系数越小,两种排序越相近。数据实验的结果显示城市列车站点的PageRank排名与城市GDP排名的逆序系数较小,两者排名较近似,从而佐证了采用分层PageRank算法计算城市列车站点的重要性是有效的。
1 数据来源
本文所使用的铁路列车班次数据来自12306网站。收集数据时,在12306允许查询的时间范围内,随机选择了对2021年4月13日的列车班次进行了查询,收集了当日国内31个直辖和省会城市之间往返列车班次数据和江西、江苏两省省内地级市之间往返列车班次数据。同时,通过百度查询采集了2020年相应各城市的GDP数据。
2 主要算法和概念
下面介绍本文的主要算法和概念,它包括用于计算城市列车站点重要性的分层PageRank算法和用于度量城市列车站点PageRank排名与城市GDP排名差异的逆序系数的概念,其基本步骤和原理分别如下:
2.1 分层PageRank算法
可以认为对于一个城市,如果开往其站点的列车越多、开往的列车班次越多,则该城市的列车站点就越重要,这一点与互联网网页排名的基本假设完全类似,所以可以采用网页的PageRank算法对各城市列车站点的重要性进行计算,它仍然是分层PageRank算法的主体思想。不过在运用PageRank算法对城市列车站点的重要性进行计算时,可以充分利用已有信息,考虑城市行政级别的层次性和特殊地位,通常直辖和省会城市能在很大程度上反映本省级行政区域与区域外的铁路连通情况。利用这一点可将我国城市铁路网络进行分层,将整个城市铁路网络划分为一些子网络(以省级行政区为子网络进行划分),再在每个子网络中选择一个重要结点(以直辖和省会城市为该结点),这些重要结点构成第1层次的铁路站点网络,而这些重要结点所在的子网络均为第2层次的铁路站点网络(有多个第2层次子网络),即把直辖和省会城市放在第一个网络层次,把各省省会和省内地级市放在第二个网络层次。直观表述如下图1所示,细线圆圈结点构成第1层次的网络,细线圆圈表示的结点就是细线圆圈所围的粗线圆圈所表示的结点中的某个重要的结点,而细线圆圈所围绕的所有粗线圆圈所表示的结点则构成了第2层次的网络。
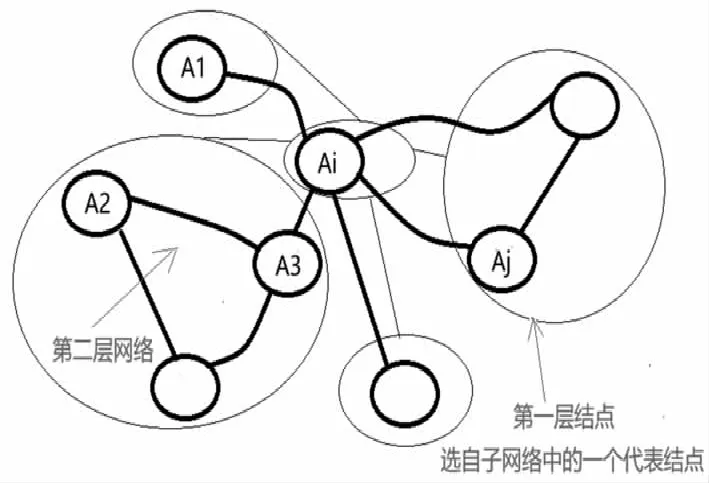
图1 分层网络示意图
分层将一个大的网络分成了若干小网络,其优点是可以并行计算第1层网络和第2层各个子网络结点的PageRank值,再综合计算出整个综合网络的PageRank值,即未分层网络的PageRank值。
分层PageRank算法步骤:
(a) 输入第1层次n个列车站点间的往返列车班次数据矩阵P={pij}n×n,其中pij是从站点j到开往站点i的班车次数。
(b) 计算第1层次n个站点间的转移概率矩阵M={mij}n×n,其中mij表示旅客从站点j到站点i的概率。根据往返列车班次数据矩阵P={pij}n×n计算转移概率的公式如下:
这里假设了旅客以等可能性乘坐从站点j开往站点i的任意一趟班次的列车。

图2 站点连接与往返列车班次示意图
为直观表述,见上图2,设有A,B,C三地站点,它们间往返列车班次数据矩阵P={pij}为

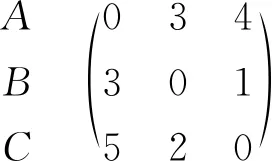
则转移概率矩阵M={mij}为
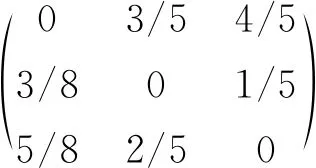
(c) 输入阻尼因子d和初始向量R0,其中d∈(0,1),此处取d=0.85,而初始向量R0=(R0(1),R0(2),…,R0(n))T设定了各个站点的初始重要性,满足

(d) 对初始向量关于转移概率矩阵做带平滑项的迭代,即
其中I表示所有分量均为1的n维向量,t=0,1,2,…。
(e) 如果Rt+1与Rt充分接近,令R=Rt+1,停止迭代。
(f) 否则,令t=t+1,继续执行(d)步。
最后得到的R=(R(1),R(2),…,R(n))T即是第1层次各个站点的PageRank值,它表示第1层次各个列车站点的重要性。
(g) 输入第1层次站点所对应的第2层次子网络中各列车站点间的往返列车班次数据矩阵,类似步骤(b)~(f),计算第2层次子网络各列车站点的PageRank值,设第2层次的第k个子网络中含有的结点数为mk,k=1,2,…,n,记它们的PageRank值为
rk=(rk(1),rk(2),…,rk(mk))Tk=1,2,…,n
注意:此步骤可以与(a)~(f)同步进行。
R(k)rk(mk))T
(1)
k=1,2,…,n。综合PageRank值的计算亦可如下表1所示。

表1 综合PageRank值的计算
2.2 逆序系数—两种排序差异的度量指标
利用上述分层PageRank算法计算各城市列车站点的PageRank值并排序,通过对比以GDP为标准而进行的城市排名,可以佐证PageRank值是否较好的反映了城市站点的重要性,这是因为城市GDP反映了城市的经济发展情况,从某种角度可以认为经济越发达的城市越重要,该城市列车站点自然也越重要,那么用城市GDP排序佐证城市列车站点的PageRank排序的关键的问题就是如何度量两种排序的差异。下面采用逆序系数来进行衡量,其思想来自定义方阵行列式时所采用的序列逆序数的概念[8],它的具体概念如下:
设有n个城市,根据其GDP排序依次为A1,A2,…,An,而根据其列车站点的PageRank值排序为Ak1,Ak2,…,Akn,其中Aki∈{A1,A2,…,An}。
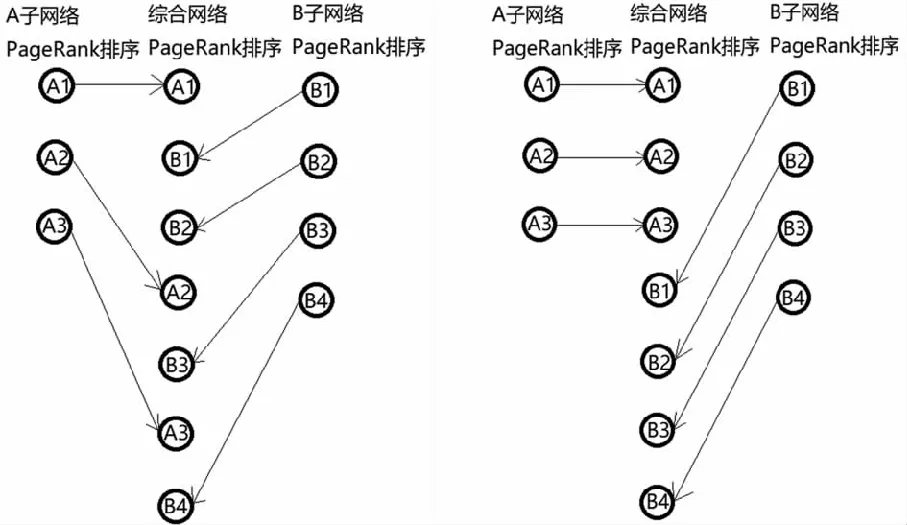
考虑自然数序列k1,k2,…,kn,如果kp>kq(p 可以看出逆序系数取值在[0,1]之内,逆序系数越小,两种排序越接近,逆序系数越大,两种排序差异越大。设有A、B两组城市,按城市的GDP排名分别为A1,A2,A3,A4和B1,B2,B3,B4,B5,如果它们列车站点的PageRank排名分别为A3,A2,A1,A4和B4,B1,B2,B3,B5,则A组城市有(3,2)、(3,1)、(2,1)这3个逆序,逆序系数为τA=3/[4(4-1)/2]=1/2;而B组城市有(4,1)、(4,2)、(4,3)这3个逆序,逆序系数为τB=3/[5(5-1)/2]=3/10,因而认为B组城市列车站点的PageRank排名比A组更接近其城市GDP排名。 根据所采集的列车班次数据,并将直辖和省会城市作为第1层网络结点,各省会城市和本省内地级市作为第2层子网络结点。由2.1节分层PageRank算法的(a)~(f)步,计算各直辖和省会城市的列车站点的第1层PageRank值如下表2的第2列,按PageRank值从大到小向下排列;表2的第3列城市名前面的序号是根据第4列GDP(单位为:亿元)从大到小排序的序号。 以城市GDP的排序序号为准,表2的城市根据列车站点的第1层PageRank值调整后,城市对应的序号列表如下,如北京对应2,郑州对应11,上海对应1等等: [2,11,1,8,7,10,19,6,9,14,12,3,18,13,23,5,20,4,26,17,21,16,24,15,22,30,28,27,25,31,29] 表2 直辖和省会城市的第1层PageRank值 由2.1节分层PageRank算法的(g)步,计算江西和江苏两省省内地级市列车站点的第2层PageRank值,如下表3和表4的第2列。 表3 江西城市第2层PageRank值 表4 江苏城市第2层PageRank值 同上,由表3与表4可知,江西和江苏两省城市站点的第2层PageRank值排序和城市GDP排序的逆序系数分别为: 由2.1节分层PageRank算法的(h)步,计算江西和江苏两省省内地级市列车站点的综合PageRank值如下表5的第2列 表5 江西、江苏两省城市综合PageRank值 由表5可知,江西江苏两省城市站点的综合PageRank值排序和城市GDP排序的逆序系数为: 对于通常PageRank的计算有许多不同的数值计算方法,例如文献[9]和[10]分别提出了一种基于子空间的启发式搜索算法和采用多幂次、多分裂的内外迭代算法。而采用2.1节分层PageRank算法对上述表2至表5中的PageRank值进行计算时,可以合并步骤(c)(d)(e)(f)。因为通过下述公式 迭代时,如果Rt+1与Rt能充分接近,说明极限存在,将上述迭代格式两边取极限(Rt→R),那么迭代计算R则变为求解线性方程组 (2) 对于线性方程组的求解,文献[11-12]归纳了多种求解算法,可以使用已有且成熟的数学工具包进行实验,其中R为PageRank值,d取0.85,n表示列车站点的个数,M表示列车站点间的转移概率矩阵,I是所有分量均为1的n维向量。 表2至表5中PageRank值计算流程图如下 图3 表2至表5中的PageRank值的计算流程图 在表2中可以看到,首都北京的第1层PageRank值排名第一,而表3和表4又可以看到江西和江苏两省的省会城市南昌和南京的第2层PageRank值都排第一,而综合PageRank值排序仍然保持子网络的原顺序,见第5节补充说明部分的图4解释.直辖和省会城市的PageRank值排名第一与铁路布局政策的倾向是吻合的。此外,在表2中还可以看到郑州铁路站点的PageRank值很大,这与郑州站是国内铁路网络的一个枢纽事实相吻合,同样的,由表3和表4可以发现上饶和苏州是江西和江苏两省省内的重要铁路交汇点,这些PageRank数据与事实的相符性在一定程度上说明了分层PageRank算法用于计算我国城市铁路站点的重要性是合理的。 更进一步的对比城市GDP排序,可以看出国内31个直辖和省会城市构成的第1层城市网络的PageRank排序和GDP排序是比较接近的,逆序系数仅为0.2,与0更接近而与1相距更远,小于0.5;第2层PageRank值(0.4、0.205128)和综合PageRank值(0.205128)也均小于0.5。这说明如果城市GDP可以反映城市的重要性(至少在经济发展角度上可以承认),那么用分层PageRank算法计算的城市站点的重要性可以从城市GDP方面得到佐证。继而可看到,江西城市站点的第2层网络逆序系数0.4比江苏城市站点的第2层网络逆序系数0.205128要大;另外,江西和江苏两省城市网络的综合PageRank排序与GDP排序的逆序系数为0.286232,恰好在江西第2层城市网络逆序系数0.4与江苏第2层城市网络逆序系数0.205128之间,说明如果把江西和江苏作为一个综合城市网络来看,两省城市站点综合网络比江苏城市站点网络变的偏离了GDP排序,但比江西城市站点网络变得贴近了GDP排序,这反映了江西铁路交通相比江苏而言有进一步提升加强的空间。这些计算结果更进一步的说明了由分层PageRank算法计算的铁路站点的PageRank值有效的刻画了列车站点的重要性。 最后需要补充说明的是,由两个第2层子网络构成的综合网络的逆序系数不一定总在第2层子网络的两个逆序系数之间,但是已知第2层子网络的逆序系数,是可以给出综合网络逆序系数的上下界估计的。推而广之,由d个第2层子网络构成的综合网络,其逆序系数的估计也可以给出,其下界估计是 (3) 而上界估计是 (4) 其中τi,ni分别表示第2层网络中第i个子网络的逆序系数和第i个子网络的结点个数,i=1,2,…,d。 为便于说明,下面以第2层三个结点的A网络和四个结点的B网络构成的综合网络逆序系数估计为例进行分析,根据2.1节分层PageRank算法(h)步的(1)式可知,子网络结点在第2层网络的PageRank排序与在综合网络中的综合PageRank排序是保持一致的,综合后可能发生两类种情况,一类是两组结点按原顺序交叉排序,一类是两组结点按原顺序分离排序,如下图4所示。 无论哪种情况,逆序个数都不会减少,而新增逆序个数要么为0,要么最多为3×4,原有的逆序数为 图4 子网络结点的综合排序示意图 τA3(3-1)/2和τB4(4-1)/2,所以综合网络的逆序个数在 之间,而综合网络的总结点数变为了3+4,所以逆序系数在 之间,其中τA,τB分别是第2层子网络A,B的逆序系数。用完全类似的推理可得,一般综合网络的逆序系数上下界估计式(3)和(4),用(3)式和(4)式计算江西和江苏两省城市综合网络的逆序系数在 之间,这与江西江苏两省综合逆序系数为0.286 232吻合。3 数据实验



4 分析与结果
5 补充说明