基于多种方法的“以电折水”系数研究

樊红梅，刘晓民，王文娟，陈琼

基于多种方法的“以电折水”系数研究

樊红梅1, 2，刘晓民1*，王文娟2，陈琼1

（1.内蒙古农业大学 水利与土木建筑工程学院，呼和浩特 010018；2.内蒙古金华源环境资源工程咨询有限责任公司，呼和浩特 010020）

【】针对目前我国农业用水占比高、计量监测难度大等问题，引入“以电折水”方法计量农业用水，推进解决农业用水的计量和核算问题。以内蒙古通辽市科尔沁区为例，采用平均值预测、多元线性回归模型、BP神经网络模型3种方法对“以电折水”系数进行预测分析，并选用平均相对误差（）、均方根误差（）、决定性系数（2）对上述3种模型比较优选。“以电折水”系数平均值预测误差平均为7.40%，预测值与实测值拟合效果较差；多元线性回归模型预测误差平均为2.40%，预测值与实测值拟合效果较好；BP神经网络模型预测误差平均值为1.65%，预测值与实测值拟合效果最好。多元线性回归模型和BP神经网络模型的、、2分别为0.024、0.175、0.923和0.018、0.131、0.957。多元线性回归模型预测精度较好，BP神经网络模型预测精度最好，平均值预测模型预测精度最差。

“以电折水”系数；平均值预测；多元线性回归；BP神经网络

0 引 言

【研究意义】农业是我国最大的经济社会用水部门，农业用水量长期占全国经济社会用水量的70%左右[1]。由于水资源禀赋条件影响，北方地区的农业用水主要依靠地下水作为供水水源。因此，农业用水管理的主要问题和首要难点是解决农业用水—特别是农业地下水取水的计量和核算问题[2]。由于农业灌溉井数量庞大且分布广泛，其用水监测难度较大，全部采用水表方式进行计量存在一次性投入工作量大、成本高和后期长效管理难等客观问题[3]。所以解决农业用水计量问题，对我国水资源开发利用具有重要意义。【研究进展】近年来，根据农业用水的特点及用水过程中存在的问题，河北省、北京市、天津市等多地提出“以电折水”的方法计量农业用水量。王向飞等[4]、王西琴等[5]通过选取典型井测试其出水量与耗电量确定“以电折水”系数，并以此推算了农业灌溉地下水开采量。陈彩明等[6]通过选取9台典型泵站率定了浙江省嘉兴市南湖灌区的“以电折水”系数。陈卫国[7]对天津市248眼典型井现场测试计算了“以电折水”系数，并对比分析与额定“以电折水”系数的关系。王剑永[8]、梁雪丽等[9]指出水泵自身特性、地下水埋深变化、农村电网变化、不同灌溉方式等都会对“以电折水”系数产生一定程度的影响。岳士茹等[10]针对“以电折水”系数计算的复杂性，提出了一种基于支持向量机的“以电折水”系数计算方法。

【切入点】已有研究多是通过布设典型灌溉井，实测用水量与用电量直接推算了“以电折水”系数的大小，采用数学模型并综合考虑其影响因素对“以电折水”系数进行预测模拟的相关研究较少。【拟解决的关键问题】鉴于此，以内蒙古通辽市科尔沁区为研究区，采用平均值预测、多元线性回归模型、BP神经网络模型3种方法对“以电折水”系数进行预测模拟，通过多种方法对“以电折水”系数进行计算，期望为“以电折水”的应用提供技术支撑及参考方法。

1 材料与方法

1.1 研究区概况

科尔沁区位于西辽河流域中下游（图1），水资源自然禀赋不足且时空分布不均，近年来随着经济社会的快速发展和灌溉面积的无序扩张，大量开采利用地下水，造成地下水位持续下降，河道断流等一系列生态问题。据统计，1990年科尔沁区有1.32万眼农业灌溉井，2019年增加为2.28万眼，而安装计量设施的5 300眼左右，仅占农业灌溉井的23.3%。主要种植作物为玉米，灌溉方式有大水漫灌、管灌、喷灌，滴灌等，灌溉面积由1990年9.9万hm2增加到2019年16.129万hm2。科尔沁区近些年来农业用水常用的统计方法是“定额法”和“以点带面法”，这2种方法主要是通过典型调查、样点灌区试验获取用水指标及灌溉水利用系数，进而推算用水总量，由于典型调查及样点灌区数量较少，统计精度难以保证。

1.2 试验方案

1.2.1 测试分区划定

研究区处于同一水文地质单元，且采用“以电折水”系数结合灌溉用电量来估算区域农业用水量，所以经综合考虑，以乡镇为基本单元，划定12个测试分区。调研摸清各测试分区的基本情况，包括农业灌溉井数量、抽水水泵型号、计量设施、灌溉方式、灌溉面积、水文地质条件、地下水埋深等。

1.2.2 典型井选取

综合考虑各测试分区内不同地下水埋深、取水条件、水泵型号、种植结构、灌溉方式等因素，按照均匀分布的原则，选取544眼典型灌溉井进行“以电折水”系数实地测试。各测试分区内每5眼典型灌溉井选择1眼作为验证样本井，其余作为训练样本井。典型灌溉井分布见图1、表1。

图1 研究区地理位置及典型灌溉井分布

表1 研究区典型灌溉井分布

1.2.3 观测指标与方法

1）基本信息调查

对所选的典型农业灌溉井进行信息采集，采集内容主要包括：灌溉井地理位置、井深、开采层位、井径、井龄等机井信息；水泵型号（功率、扬程、流量）、泵龄、下泵深度等水泵信息；灌溉方式、控制面积、主要作物等灌溉信息。

2）埋深、井深测量

采用测绳对典型灌溉井的地下水埋深、井深进行测量。

3）出水量测量

采用手持式超声波流量计并结合已安装计量设施对典型灌溉井出水量进行测量，开泵30 min待出水量稳定后开始测定出水量，每隔10 min读取1个出水量数值，连续测定24 h。

4）用电量测量

采用典型灌溉井安装的电表直接读取用电量，与出水量同步读取用电量数值，连续测定24 h。

1.3 研究方法

根据各测试分区典型灌溉井的实测数据，以训练样本井数据建立数学模型对“以电折水”系数进行预测，分析与实测值对比的误差情况，选用、、2优选模型，并以验证样本井数据对最优模型进行预测精度验证。本文主要采用3种数学模型：平均值预测、多元回归模型以及BP神经网络模型。

1.3.1 平均值预测

平均值预测是指利用过去实际发生的变动资料求得平均值，作为下期的预测值。

1.3.2 多元线性回归模型

多元线性回归模型是分析多个变量之间的线性或非线性的一种数学模型，是选取多个变量作为自变量，一个变量作为因变量，并模拟分析他们之间的相关关系的一种统计分析方法，其表达式为：

01122……+βx+ε， （1）

采用最小二乘法对上式中的待估回归系数1，2，……，β进行估计，求得值，并对模型进行拟合，若模型拟合越好，则预测的变量越接近实际值。

图2 BP神经网络的拓扑结构图

1.3.3 BP神经网络模型

BP神经网络是一种按照误差逆向传播算法训练的多层前馈网络，采用最速下降法，通过反向传播算法不断调整网格权值和阈值，使网络的误差平方和最小，使输出值尽可能与期望值接近[11]。BP神经网络模型拓扑结构包括输入层、隐层、输出层（图2）。

1.3.4 模型评价指标

本文选用2作为模型的评价标准[12～13]，均反映实测值与模型预测值之间差异程度，越接近0，说明模型预测的效果越好；2反映实测值与预测值之间的相关程度，2越接近1，说明预测值对实测值的解释程度越高。计算式为：

2 结果与分析

2.1 相关性分析

根据各测试分区典型灌溉井的实测数据，选取地下水埋深、井龄、泵龄、井深、灌溉方式（滴灌取为1，喷灌取为2，管灌取为3，大水漫灌取为4）、水泵额定功率、扬程、流量与“以电折水”系数做相关性分析（表2、图3）。可以看出，地下水埋深、井龄、泵龄、井深、额定扬程与“以电折水”系数呈负相关；灌溉方式、额定功率、额定流量呈正相关。地下水埋深、泵龄、灌溉方式与“以电折水”系数相关性较好；井龄、井深相关性一般；水泵额定功率、扬程、流量相关性较差。

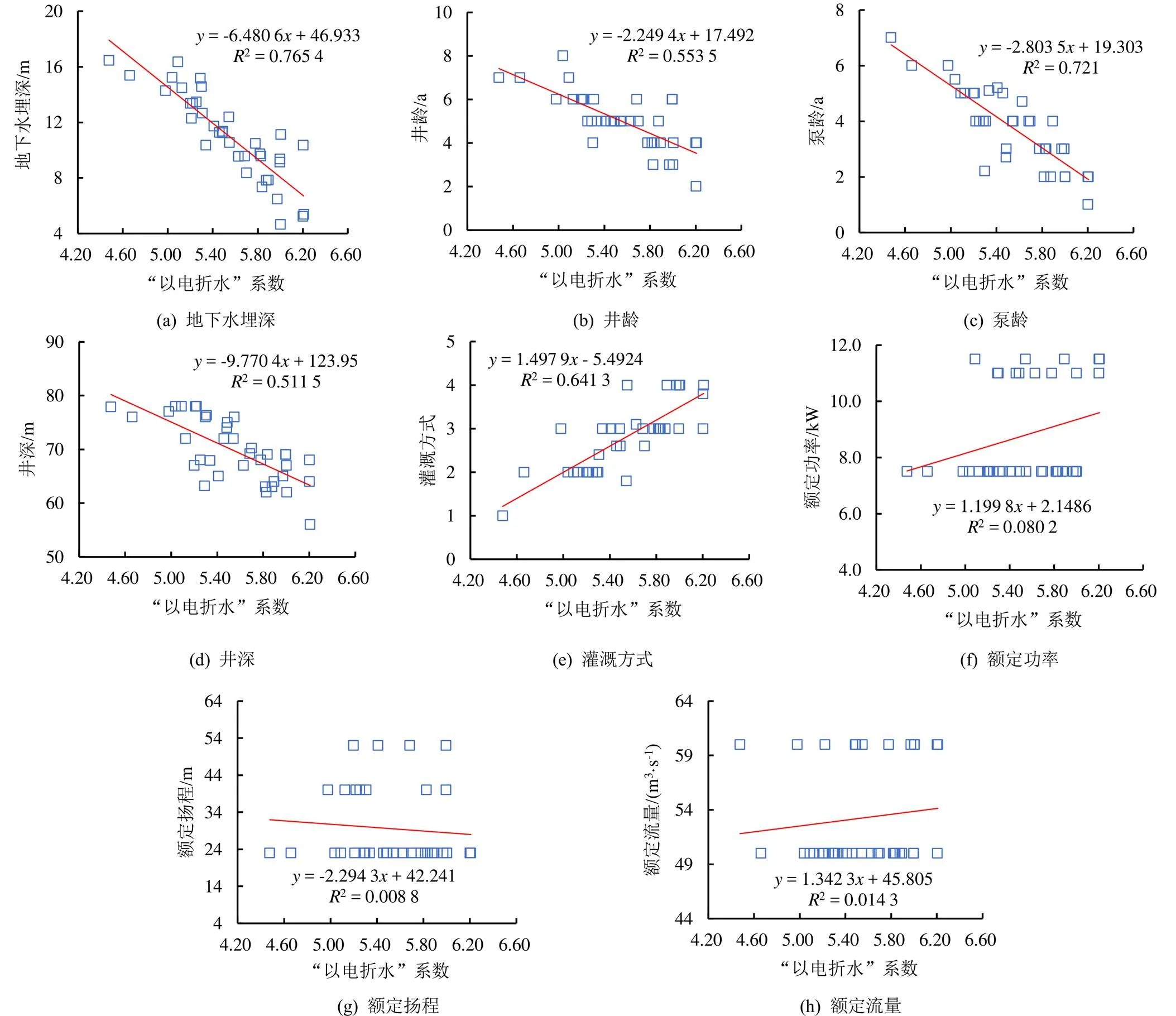
图3 测试分区Ⅰ“以电折水”系数与影响因素相关性分析

2.2 平均值预测

以各测试分区训练样本井“以电折水”系数的平均值作为预测值，与实测值对比的误差情况见表3。

表3 平均值预测误差表

由表3可知，研究区预测误差最大值为35.33%，最小值为0.04%，平均值为7.40%，平均值预测误差较大，拟合效果较差。

2.3 多元线性回归模型

根据上述“以电折水”系数的与影响因素的相关性分析，地下水埋深、泵龄、灌溉方式与“以电折水”系数相关性较好，并且地下水埋深越大，水泵使用的时间越长，“以电折水”系数越小，不同灌溉方式对“以电折水”系数影响也较大，所以以各测试分区训练样本井的地下水埋深（1）、泵龄（2）、灌溉方式（3）为自变量，“以电折水”系数为因变量（），建立多元线性回归模型：

123。 （5）

多元回归模型回归公式、决定参数及显著性检验见表4，多元归回预测值与实测值对比的误差情况见表5，预测效果见图4。

由表5可知，研究区预测误差最大值为13.41%，最小值为0.01%，平均值为2.40%，多元线性回归预测误差较小。由图4可知，预测值与实测值拟合效果较好，少数典型井预测值与实际值误差较显著。

表4 多元回归模型结果

表5 多元回归模型预测误差表

图4 多元回归模型预测效果图

2.4 BP神经网络模型

以各测试分区训练样本井的地下水埋深、井龄、泵龄、井深、灌溉方式为输入项，以“以电折水”系数为输出项，建立BP神经网络模型对“以电折水”系数进行预测。模型最小训练速率为0.1，动态参数为0.6，参数sigmoid为0.9，允许误差为0.000 1，最大迭代次数为1 000，采用3层网络结构，输入单元数为5，输出单元数为1，隐含层单元数根据“试错法”确定，经试算，隐含层单元数6时训练效果较好。预测值与实测值对比的误差情况见表6，BP神经网络模型预测效果见图5。

由表6可知，研究区预测误差最大值为11.28%，最小值为0.01%，平均值为1.65%，BP神经网络模型预测误差较小；由图5可知，预测值与实测值拟合效果较好。

图5 BP神经网络模型预测效果图

表6 BP神经网络模型预测误差表

2.5 模型比较与验证

对上述3种模型计算平均相对误差（）、均方根误差（）、决定性系数（2）进行预测精度对比分析（表7）。

表7 多种方法预测精度对比

由表7可知，平均值预测精度最差，最大，说明实测值与预测值之间误差最大，不具有可靠性；2最小，说明实测值与预测值的相关程度最差。平均值预测计算简单，但容易受极大、极小值的影响，预测精度较低。当区域内“以电折水”系数波动较小且无法获得其影响因素时可采用该方法进行预测。

多元线性回归模型预测精度较好，较小，说明实测值与模型预测值之间误差较小；2较大，说明实测值与预测值的相关程度较好。多元线性回归模型可以建立多组变量间的线性因果关系，便于分析，但忽略了交互效应和非线性的因果关系。当已知地下水埋深、泵龄、灌溉方式等影响“以电折水”系数的因素且实测样本较多时可采用多元线性回归模型进行预测。

BP神经网络模型预测精度最好，最小，说明实测值与模型预测值之间误差最小；2最大，说明实测值与预测值的相关程度最好。BP神经网络模型具有较强的非线性映射能力，能够逼近任何非线性连续函数，所以实测样本较多且获得“以电折水”系数影响因素时采用BP神经网络模型预测效果最好。

以各测试分区验证样本井数据对BP神经网络模型进行预测精度验证，结果见表8。

表8 BP神经网络模型预测精度验证

由表8可知，BP神经网络模型验证效果较好，各测试分区相对误差均小于5%，说明拟合效果较好；均较小，说明实测值与预测值之间差异程度较小；2均较大，说明预测值对实测值的解释程度较高。在实际应用中，“以电折水”系数影响因素较多，虽然BP神经网络模型预测精度最好，但其缺乏物理机制，可能导致预测结果不稳定，所以也可以通过变换不同的自变量采用多元回归模型进行预测模拟。

3 讨 论

“以电折水”系数受多种因素影响，根据能量守恒定律，在耗能一定的情况下，水泵扬程与流量呈反比关系；农业灌溉井的深度一般与地下水埋深有一定的联系，地下水埋深比较大的区域机井一般较深，其对应的“以电折水”系数相对较小。尹世洋等[14]在北京市平原区进行“以电折水”系数影响因素分析，得出地下水埋深越小、含水层富水性越好的区域“以电折水”系数越大，本文与其研究结果一致。农业灌溉井、水泵年龄越大，说明使用的时间越长，且设施老化越严重，则机井出水量就会减少，其相应的“以电折水”系数也会减小，所以井龄、泵龄与“以电折水”系数呈负相关，岳士茹等[10]在河北省平原区进行“以电折水”研究也得到相同的结果。不同灌溉方式下灌溉系统压力不同，水泵工作环境也不同，对应的“以电折水”系数的大小也不同，梁雪丽等[9]也证明了“以电折水”系数大小与灌溉系统压力呈负相关。

本文采用平均值预测、多元线性回归模型、BP神经网络模型3种方法对“以电折水”系数进行预测模拟，由于“以电折水”系数受多种因素影响，所以每一眼农业灌溉井的“以电折水”系数大小不一，故采用各测试分区平均值代替每眼井的“以电折水”系数会有较大误差[8]。多元线性回归模型与BP神经网络模型考虑了“以电折水”系数影响因素对其进行预测，故误差较小，拟合效果较好。

多元线性回归模型利用线性来拟合多个自变量和因变量的关系，确定多元线性回归模型的参数，从而回归至原假设方程中，通过回归方程来预测因变量的趋势。BP神经网络模型具有良好的非线性映射逼近性能，用于构建变量间的非线性模型，可以处理复杂空间的非线性系统，受样本空间分布影响较小，它通过调整内部的权重来提高网络优化的效果，所以BP神经网络模型的非线性映射关系对变量的处理效果优于多元线性回归模型的线性关系，使得其预测结果具有更高的精度和应用范围，这也与许多学者的研究成果[15-16]相符。

4 结 论

1）选取典型灌溉井的地下水埋深、井龄、泵龄、井深、灌溉方式、水泵额定功率、扬程、流量与“以电折水”系数做相关性分析，地下水埋深、泵龄、灌溉方式与“以电折水”系数相关性较好；井龄、井深相关性一般；水泵额定功率、扬程、流量相关性较差。

2）通过采用平均值预测、多元线性回归模型、BP神经网络模型3种方法对“以电折水”系数进行预测模拟，平均值预测精度最差；多元线性回归模型预测精度较好；BP神经网络模型预测精度最好。

3）研究区域内“以电折水”系数波动较小且无法获得影响因素时可采用平均值进行预测；已知地下水埋深、泵龄、灌溉方式等影响“以电折水”系数的因素且实测样本较多时可采用多元线性回归模型、BP神经网络模型进行预测。

[1] 沈莹莹, 张绍强, 吉晔. 我国农业灌溉用水量统计方法的确定及工作开展情况[J]. 中国农村水利水电, 2016 (11): 133-134, 138.

SHEN Yingying, ZHENG Shaogang, JI Ye. Determination of statistical method of agricultural irrigation water consumption and its development in China[J]. China Rural Water and Hydropower, 2016 (11): 133-134, 138.

[2] 沈波, 吉庆丰, 张玉建, 等. 农业灌溉用水计量方法研究[J]. 江苏水利, 2017(4):13-17.

SHEN Bo, JI Qingfeng, ZHNG Yujian, et al. Study on measurement method of agricultural irrigation water[J]. Jiangsu Water Resources, 2017(4): 13-17.

[3] 李娜. 关于农业灌溉用水计量方法的探讨[J]. 水科学与工程技术, 2014(6): 69-71.

LI Na. Research on Water Measurement in Agricultural Irrigation[J]. Water Sciences and Engineering Technology, 2014(6): 69-71.

[4] 王向飞. 电水转换在地下水开采量计量中的应用-以河北省沧县为例[J]. 地下水, 2014, 36(6): 76-77.

WANG Xiangfei. The application of electricity water conversion in the measurement of groundwater exploitation: a case study of Cangxian County, Hebei Province[J]. Ground water, 2014, 36(6): 76-77.

[5] 王西琴, 张馨月, 陈浩. 华北地下水超采区粮食作物灌溉用水量及其节水潜力：基于河北省620户问卷调研数据[J]. 西北大学学报(自然科学版), 2020, 50 (2): 227-233.

WANG Xiqin, ZHANG Xinyue, CHEN Hao. Irrigation water consumption and water-saving potential of food crops in groundwater over-exploitation areas in North China: Based on survey data of 620 households in Hebei Province[J]. Journal of Northwest University (Natural Science Edition), 2020, 50(2): 227-233.

[6] 陈彩明, 李其峰, 陈欣, 等. 基于“以电折水”及灌溉回归水重复利用的农田灌溉用水量统计方法研究[J]. 中国农村水利水电, 2019(9): 68-71.

CHEN Caiming, LI Qifeng, CHEN Xin, et al. Research on the statistical method of irrigation water consumption for farmland based on “Conversion of Electricity to Water” and irrigation return water[J]. China Rural Water and Hydropower, 2019(9): 68-71.

[7] 陈卫国. 天津市地下水机井泵以电折水系数测算分析研究[J]. 海河水利, 2019(5): 42-47.

CHEN Weiguo. Calculation and analysis of electric water conversion coefficient of underground water pump in Tianjin[J]. Haihe Water Resources, 2019(5): 42-47.

[8] 王剑永. “以电折水”方法研究与应用[J]. 中国水利, 2017(11): 34-35.

WANG Jinayong. Research and application of “electricity water reduction”[J]. China Water Resources, 2017 (11): 34-35.

[9] 梁雪丽, 吕旺, 兰凤. 以电折水系数影响因素探析-以不同灌溉方式为例[J]. 海河水利, 2019(1): 68-70.

LIANG Xueli, LYU Wang, LAN Feng. Analysis of influencing factors of electric water conversion coefficient-taking different irrigation methods as an example[J]. Haihe Water Resources, 2019(1): 68-70.

[10] 岳士茹, 郄志红, 刘印良, 等. 基于SVM的河北省平原区水电转换系数内插预测研究[J]. 河北农业大学学报, 2020, 43(1): 133-147.

YUE Shiru, QIE Zhihong, LIU Yinliang, et al. Interpolation prediction of conversion coefficient between the consumed electricity and pumped water in Hebei plain based on SVM[J]. Journal of Hebei Agricultural University, 2020, 43(1): 133-147.

[11] 赵文刚, 马孝义, 刘晓群, 等. 基于神经网络算法的广东省典型代表站点0简化计算模型研究[J]. 灌溉排水学报, 2019, 38(5): 91-99.

ZHAO Wengang, MA Xiaoyi, LIU Xiaoqun. et al. Using Neural Network Model to Simplify0Calculation for Representative Stations in Guangdong Province[J]. Journal of Irrigation and Drainage, 2019, 38(5): 91-99.

[12] 张晓斌, 李抗彬, 郝改瑞, 等. 基于BP神经网络的新安江模型初始土壤蓄水量计算研究[J]. 灌溉排水学报, 2021, 40(3): 15-22.

ZHANG Xiaobin, LI Kangbin, HAO Gairui, et al. Using BP Network to Estimate Initial Soil Water Storage in Xin’anjiang Model[J]. Journal of Irrigation and Drainage, 2021, 40(3): 15-22.

[13] 曹秀佳, 谷健, 马宁宁, 等. 基于粒子群优化小波神经网络模型的春玉米生育阶段干旱预测[J]. 灌溉排水学报, 2021, 40(3): 125-133.

CAO Xiujia, GU Jian, MA Ningning, et al. Predicting Droughts in Growth Season of Spring Maize with the Wavelet Neural Networks using Particle Swarm Optimization Training[J]. Journal of Irrigation and Drainage, 2021, 40(3): 125-133.

[14] 尹世洋, 吴文勇, 刘洪禄, 等. 北京市平原区农用机井水电折算系数试验研究[J]. 排灌机械工程学报, 2014 (11): 998-1 004.

YIN Shiyang, WU Wenyong, LIU Honglu, et al. Experiments on conversion coefficient between electricity consumed and water pumped for agricultural wells in Beijing plain[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014 (11): 998-1 004.

[15] 赵金元, 马振, 唐海亮, 等. BP神经网络和多元线性回归模型对碳排放预测的比较[J]. 科技和产业, 2020, 20(11): 172-176.

ZHAO Jinyuan, MA Zhen, TANG Hailiang, et al. Comparison of BP Neural Network and Multiple Linear Regression Models for Carbon Emissions Prediction[J]. Science Technology and Industry, 2020, 20(11): 172-176.

[16] 佟秀秀, 康志宏. 基于多元线性回归和BP神经网络的单井能力预测[J]. 科学技术与工程, 2019, 19(29): 96-102.

TONG Xiuxiu, KANG Zhihong. Single Well Capacity Prediction Based on Multiple Linear Regression and Back Propagation Neural Network[J]. Science Technology and Engineering, 2019, 19(29): 96-102.

Estimating Water Consumption from Electricity Consumption:How to Calculate the Conversion Coefficient

FAN Hongmei1,2, LIU Xiaomin1*, WANG Wenjuan2, CHEN Qiong1

(1.School of Water Conservancy and Civil Engineering, Inner Mongolia Agricultural University, Hohhot 010018, China;2.Inner Mongolia Jinhuayuan Environmental Resources Engineering Consulting Co., Ltd, Hohhot 010020, China)

【】Agriculture is the largest water-consuming sector in China, but how to estimate agricultural water use is an issue that remains extremely difficult despite its importance in improving water measurement. Considering that moving water for irrigation needs power, an alternative method emerging over the past decades is to estimate it based on the electricity reading on the national grid. The purpose of this paper is to investigate how to estimate the conversion coefficient of this method.【】We took Horqin District at Tongliao City in Inner Mongolia as an example. We calculated the conversion coefficient using the multiple linear regression model and the BP neural network model respectively, with the standard average method taken as the control (CK). For each method, the average relative error (), root mean square error () and decisive coefficient (2) were selected as indicators to compare the above models.【】The error of the standard average method was 7.40%. In contrast, the relative error of the multiple linear regression model and the BP neural network models was 2.40% and 1.65%, respectively. These results indicated that it is feasible to estimate agricultural water consumption using the electricity consumption read from the national grid. Among the three methods we compared, the BP neutral network was most accurate for estimating the conversion coefficient.【】The MRE, RMSE and R2of the multiple linear regression model were 0.024, 0.175 and 0.923 respectively, compared with their associated values in the BP neural network model, which were 0.018, 0.131 and 0.957. The BP neural network can thus be used as a robust method to estimate the conversion coefficient in converting electricity consumption to agricultural water consumption.

converting electricity to water; conversion coefficient; multiple linear regression; BP neural network

S275

A

10.13522/j.cnki.ggps.2021202

樊红梅, 刘晓民, 王文娟, 等. 基于多种方法的“以电折水”系数研究[J]. 灌溉排水学报, 2021, 40(11): 98-105.

FAN Hongmei, LIU Xiaomin, WANG Wenjuan, et al. Estimating Water Consumption from Electricity Consumption: How to Calculate the Conversion Coefficient[J]. Journal of Irrigation and Drainage, 2021, 40(11): 98-105.

1672 - 3317（2021）11 - 0098 - 08

2021-05-13

国家重点研发计划子课题（2018YFC0406404-3）；国家自然科学基金项目（51969021）；内蒙古自治区科技重大专项（2020ZD0009-4）

樊红梅（1993-），女。硕士研究生，主要从事水资源合理配置研究。E-mail: 1258484546@qq.com

刘晓民（1981-），男。副教授，硕士生导师，主要从事水资源合理配置与水库优化调度研究。E-mail: 13204717007@163.com

责任编辑：白芳芳