基于DWT-WFGM(1,1)-ARMA组合模型的农业用水量预测

王冠智，粟晓玲*，张特，姜田亮，褚江东

基于DWT-WFGM(1,1)-ARMA组合模型的农业用水量预测

王冠智1,2，粟晓玲1,2*，张特1,2，姜田亮1,2，褚江东1,2

（1. 西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2. 西北农林科技大学 旱区农业水土工程教育部重点实验室，陕西 杨凌 712100）

农业用水量预测对于区域水资源规划与管理具有重要意义。【】针对农业用水量序列的振荡性以及传统模型预测结果输出单一的问题，提出一种新的组合预测模型DWT-WFGM(1,1)-ARMA对区域农业用水量进行预测。通过离散小波变换将原始用水量序列分解为近似序列和细节序列，并分别采用自回归滑动平均模型和分数阶灰色模型预测细节序列和近似序列，并结合加权马尔可夫链对近似序列进行误差修正，将不同成分序列的预测结果进行线性叠加得到农业用水量的预测值和预测区间。利用该模型分别对陕西省和内蒙古自治区的农业用水量进行预测，并与灰色模型GM(1,1)、DWT-GM(1,1)-ARMA模型和DWT-FGM(1,1)-ARMA模型对比分析。DWT-WFGM(1,1)-ARMA模型在陕西省和内蒙古自治区的评价指标平均绝对百分比误差分别为1.25%和1.01%，预测精度高于其他模型，且预测区间为研究区未来时期的农业用水量提供了合理的波动范围，具有一定的实际参考价值。本文构建的组合模型能够有效提高农业用水量预测的精度，同时预测区间的提出可以为区域农业用水量预测提供更加可靠的依据。

农业用水；分数阶灰色模型；加权马尔可夫链；离散小波变换；预测区间

0 引 言

【研究意义】农业用水是国家粮食安全的重要保障[1]。近年来，随着社会经济发展和城市化进程的加快，工业和生活用水量逐年增加，农业用水的供需压力不断增大。同时，由于人们对水资源规划的重视程度不足，导致灌溉用水效率低下与农业用水短缺等问题并存[2]。农业用水预测是进行水资源规划、配置和管理的工作基础，准确预测农业用水量可以为区域水资源的高效管理与合理配置提供有力的支撑。

【研究进展】农业用水量预测方法众多，其中定额法、时间序列法、神经网络法以及灰色模型等方法已得到广泛的应用[3-5]。农业用水量受气候变化、经济发展、科技进步等多方面因素的影响，序列通常呈现振荡趋势，单一模型难以体现其非线性特征，影响预测精度[6-8]。组合模型结合多种模型的优势，可有效提高预测结果的准确性[9]。在用水预测组合模型中，小波变换与其他方法的耦合模型取得了较好的预测效果[10-12]。其中，最常见的小波组合模型DWT-GM(1,1)-ARMA通过小波分解将振荡序列的预测转化为灰色模型（Grey Model，GM(1,1)）与自回归滑动平均（Autoregressive Moving Average Model，ARMA）模型的分量预测。如佟长福等[10]构建DWT-GM(1,1)-ARMA模型对中国农业需水量进行预测，取得了较好的精度；邓权龙等[11]对矿区用水量预测的研究结果也表明该模型具有良好的预测性能。【切入点】然而，农业用水量的影响因素具有阶段性，使得用水序列在不同时段呈现出不同的变化趋势，而灰色模型GM(1,1)在分量预测过程中对各时段的用水序列信息赋予相同权重，无法准确反映用水变化的内部规律，样本中的数据信息未得到充分挖掘[13-14]。分数阶灰色模型（Fractional Order Grey Model，FGM(1,1)）是在GM(1,1)模型基础上提出的新型灰色预测模型，具有新信息优先、预测扰动小等特点，广泛应用于众多领域的预测工作中[15-17]，而目前尚未引入用水量的预测研究。此外，DWT-GM(1,1)-ARMA模型仅以预测值作为模型的输出结果，而单一的预测值无法提供更多的信息，模型有待进一步改进。

【拟解决的关键问题】针对农业用水量序列的振荡性以及传统模型预测结果输出单一的问题，本文在DWT-GM(1,1)-ARMA小波组合模型的基础上，将离散小波变换（Discrete Wavelet Transform，DWT）、加权马尔可夫链（Weighted Markov Chain，WMC）、改进的分数阶灰色模型（WFGM(1,1)）和自回归滑动平均模型相结合，提出DWT-WFGM(1,1)-ARMA组合模型，并应用于陕西省和内蒙古自治区农业用水量预测中，以期为农业用水规划提供技术支撑。

1 研究区域和数据来源

农业用水（包括农田灌溉及林牧渔畜用水）为陕西省（31°42′—39°35′N，105°29′—111°15′E）和内蒙古自治区（37°24′—53°23′N，97°12′—126°04′E）的主要用水户，分别占两省总用水量的60%和70%以上。本文以这两省区的农业用水为研究对象，对农业用水量进行预测。历史用水数据分别来源于两省区2002—2019年的水资源公报。

2 研究方法

2.1 离散小波变换

小波变换是一种时频信号局部化分析的方法，通常分为连续小波变换（CWT）和离散小波变换（DWT）2类[18]。由于时间序列一般是离散的，实际应用中经常采用离散小波变换：

式中：()为时间序列；为序列长度；*()为小波函数()的共轭复数；(,)为离散小波系数，为确定小波伸缩与平移幅度的整数。

通过离散小波变换对原始序列进行分解得到反映序列趋势性的近似序列A和由随机成分构成的细节序列（1、2,…,D）二部分，如图1所示。

图1 三层离散小波变换

在小波函数选择上，Daubechies（dbN）小波具有正交性、高正则性等特点，在非平稳序列的分解上具有较好的效果；在分解层数选择上，小波分解层数越多，序列的平稳性越好，但由于分解过程存在误差，层数越多，误差越大，因此分解层数一般采用2～4层[19]，本文选取为3层。

2.2 分数阶灰色预测模型FGM(1,1)

模型时间响应式为：

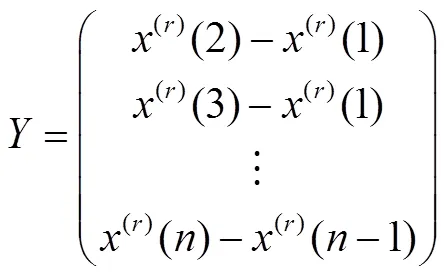
分数阶灰色模型FGM(1,1)的阶数对模型的预测性能有较大的影响，为了获得最优阶参数，通常以“最优拟合”为优化目标函数：

式中：()表示模型对历史序列的拟合程度。

2.3 基于加权马尔可夫链修正的分数阶灰色模型WFGM(1,1)

为了最大程度挖掘近似序列中的有效信息，本文将加权马尔可夫链理论应用到分数阶灰色模型预测中，修正分数阶灰色模型预测的结果，达到改善模型预测精度的目的。

2.3.1 FGM(1,1)模型误差状态区间的划分

FGM(1,1)模型预测值与序列实际值的相对误差（=12,…,）呈非规律性变化，将划分为个状态区间，任意误差状态区间可以表示为：

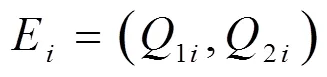
式中：E为第种状态，2i和1i分别为E状态的上、下界。

采用最优分割法对误差状态区间进行划分，以“组内差异最小、组间差异最大”为划分依据，通常定义分类误差函数为：

式中：为样本数目，为状态区间的分类数目，(d,d+1-1)为样本的离差平方和，具体计算可参考文献[21]。其中，通常通过[(,)]曲线图确定，曲线拐点处的即为状态区间的最优分类数目。

2.3.2 自相关系数和权重的计算

设状态E出现的次数为S，由状态E经过步到状态E的次数为S，则由状态E到E的转移概率为：

得到×阶的状态转移概率矩阵()，记作：

为反映各阶步长对马尔可夫链修正值的影响权重，采用的各阶自相关系数反映权重的大小：

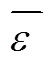
2.3.3 WFGM(1,1)模型预测

式中：,,∈,,,≤。

将同一状态下的各转移概率加权和作为预测相对误差d的转移概率：

取P最大值所处的状态即为下一阶段预测相对误差d的加权马尔可夫状态。以此类推，可得到未来多年的预测误差区间，根据误差区间的中值和边界值可得到近似序列的预测值()和预测区间()：

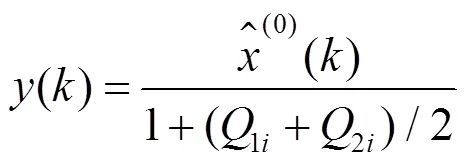
2.4 自回归滑动平均模型（ARMA）

ARMA模型广泛应用于时间序列的预测分析，模型不仅能够有效地捕捉离散小波分解后时间序列的随机成分，同时具有结构简单、高效等优点，对细节序列预测具有良好的适用性，ARMA(,)模型计算式为：

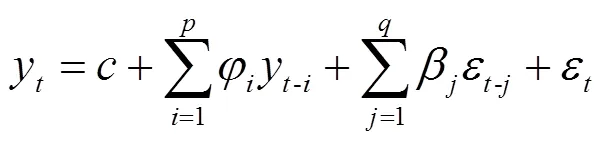
2.5 DWT-WFGM(1,1)-ARMA模型

农业用水组合预测模型由离散小波变换、加权马尔可夫链修正的分数阶灰色模型和自回归滑动平均模型组成。通过离散小波变换对原始序列进行分解，并对分解后的2种成分序列分别采用不同的方法进行预测。具体步骤如下：

步骤1：采用离散小波变换对原始用水序列进行处理，得到一个近似序列A和若干个细节序列（1,2…,D）。

步骤2：对近似序列A采用基于加权马尔可夫链修正的分数阶灰色模型WFGM(1,1)进行预测。首先，以“最优拟合”为准则计算得到模型最优阶数（当=1时，FGM(1,1)模型转化为GM(1,1)模型），在最优FGM(1,1)模型预测得到初步预测值后结合加权马尔可夫链划分序列的误差区间，推求未来用水序列所处的误差状态区间，并根据预测误差状态区间的中值和边界值求得近似序列A的预测值及预测区间，预测值和预测区间的计算式见式（16）和式（17）。

步骤3：对于细节序列1、2,…,D，根据赤池信息准则（Akaike information criterion，AIC）建立ARMA模型进行预测，具体见式（18）。

步骤4：将细节序列和近似序列的预测结果线性叠加，得到最终的预测值和预测区间。

模型详细操作流程如图2所示。

图2 基于DWT-WFGM(1,1)-ARMA的农业用水预测模型流程

图3 农业用水序列成分分解结果

图4 近似序列A3拟合结果

3 模型应用和结果分析

以2002—2015年为模型训练期，2016—2019年为模型验证期，并选择均方根误差（）、平均绝对误差（）和平均绝对百分比误差（）作为模型精度的评价标准。

3.1 离散小波分解

根据农业用水的序列特征，采用db4小波对原始序列进行3层分解，分别得到陕西和内蒙古二省区原始序列时间尺度为3的近似序列3和细节序列1、2和3，见图3。

3.2 近似序列预测

3.2.1 最优阶数的确定

确定FGM(1,1)的最优阶数需要进行大量计算，本文采用粒子群优化（PSO，Particle Swarm Optimization）算法对模型阶数进行计算。结果表明，当陕西省和内蒙古自治区的模型阶数分别为0.893 3和1.0时，模型在训练期的模拟效果最好，如图4所示。

3.2.2 加权马尔可夫链修正分析

图5 分类误差曲线

根据2012－2015年的概率转移矩阵和误差状态对2016年所属状态进行预测。由表1可知，2016年的相对误差属于2状态，根据式（16）和式（17）计算得到修正值为57.70亿m3，近似预测区间为(57.18, 58.24)。同理对其他年份进行预测，以此类推得到对应年份近似序列的修正值和预测区间，见表2。

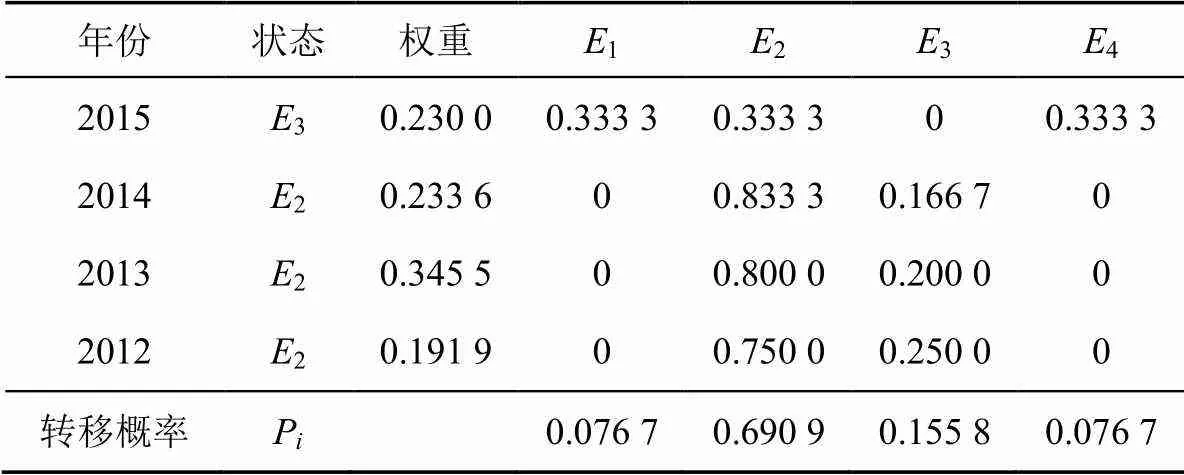
表1 2016年相对误差状态预测

表2 加权马尔可夫链修正结果

3.3 细节序列预测

利用SPSS软件构建ARMA(,)模型对细节序列进行预测，依据AIC准则确定模型阶数和，最终确定陕西省农业用水预测模型为ARMA(2,1)、ARMA(1,2)以及ARMA(2,2)，内蒙古农业用水预测模型为ARMA(2,1)、ARMA(2,1)以及ARMA(1,2)，拟合结果如图6所示。

图6 细节序列拟合结果

3.4 结果与分析

将近似序列和细节序列的预测结果叠加后得到农业用水量预测的最终结果，包括预测值和预测区间，如表3所示。从表3可以看出，2016—2018年陕西省农业用水量、2016—2017年内蒙古自治区农业用水量均在相应预测区间内，而2019年陕西省农业用水量和2018—2019年内蒙古自治区农业用水量未在预测区间内。这是由于加权马尔可夫链在对未来误差状态区间进行预测时，会以验证期中预测所得的非确定状态为基础状态对未来状态区间进行判断，预测年限越长，基础状态中的不确定状态越多，使得区间预测的不确定性随着预测年限的增长而不断增大，进而导致验证期后期的区间预测失准。总的来说，加权马尔可夫链能够在短期（3 a）内对未来误差状态做出较为准确的判断，并在修正农业用水量预测值的同时提供合理的预测区间。

为了进一步检验本文提出的DWT-WFGM(1,1)-ARMA模型的预测性能，以相同的原始数据为基础，选择GM(1,1)模型、DWT-GM(1,1)-ARMA模型、DWT-FGM(1,1)-ARMA模型以及DWT-WFGM(1,1)-ARMA模型进行对比分析。模型预测结果对比如图7所示，预测性能对比结果如表4所示。

由图7可知，相比其他模型，本文提出的DWT-WFGM(1,1)-ARMA模型能够更好地拟合农业用水量的变化趋势，具有更好的预测效果。

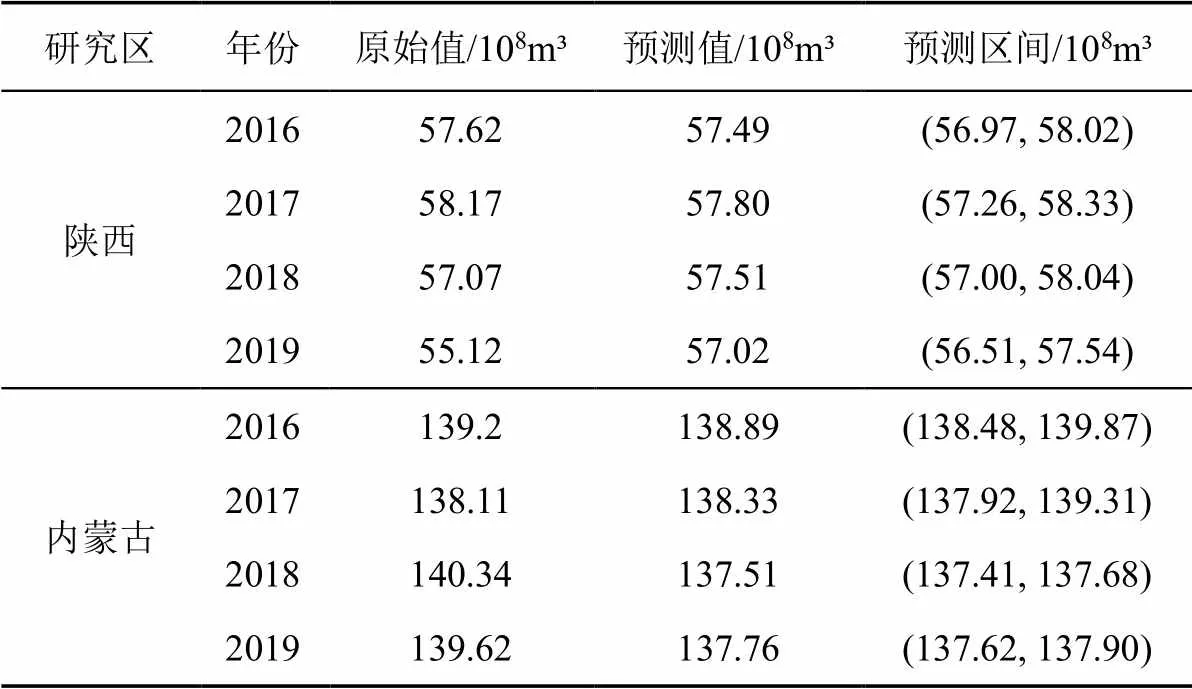
表3 农业用水预测区间

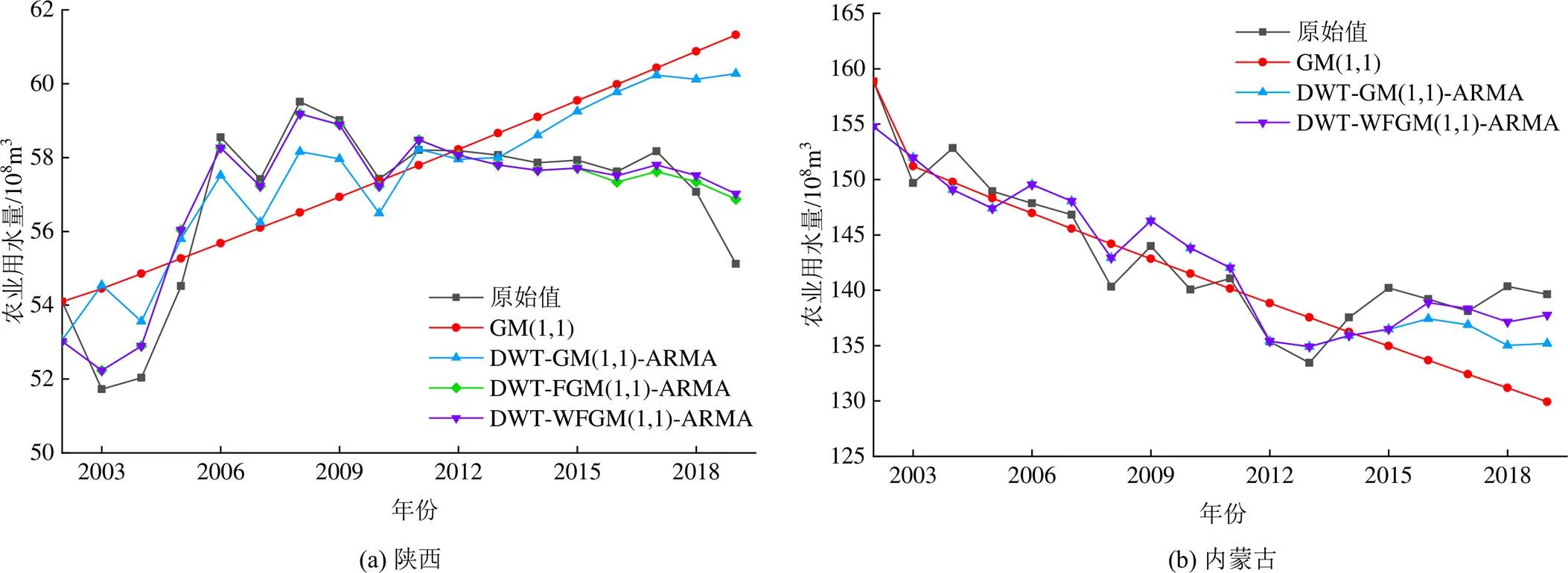
图7 不同模型预测效果对比

表4 预测结果精度评价

由表4可知，本文提出的DWT-WFGM(1,1)-ARMA模型的评价指标整体优于其他模型。相同条件下DWT-GM(1,1)-ARMA模型与GM(1,1)模型相比，评价指标、和在陕西省分别降低了14.9%、13.5%和13.7%，在内蒙古自治区分别降低了51.7%、58.8%和57.5%，这是由于离散小波变换处理可以降低原始序列的波动性，同时ARMA模型能够对序列中的随机成分进行有效的捕捉，在一定程度上提高了模型的预测精度。相同条件下DWT-FGM(1,1)-ARMA模型与DWT-GM(1,1)-ARMA模型相比，评价指标、和在陕西省分别降低了84.2%、84.8%和84.9%，在内蒙古自治区未发生变化（当=1时，FGM(1,1)模型转化为GM(1,1)模型），说明FGM(1,1)模型能够有效利用数据中的新信息，进一步优化模型的预测性能。相同条件下DWT-WFGM(1,1)-ARMA模型与DWT-FGM(1,1)-ARMA模型相比，评价指标在陕西省提高了9.5%，和分别降低了6.3%、3.9%，评价指标、和在内蒙古自治区分别降低了48.9%、60.3%和55.9%，说明加权马尔可夫链能够挖掘残差序列中有价值的信息，并在短期内对序列误差状态区间做出较为准确的判断。综上所述，DWT-WFGM(1,1)-ARMA模型能够解决传统模型预测精度低、输出结果单一的问题，对农业用水量预测具有良好的适用性。

4 讨 论

本研究在DWT-GM(1,1)-ARMA模型的基础上提出了新的农业用水量预测模型DWT-WFGM(1,1)-ARMA模型。经检验，新模型能够在提高预测精度的同时为区域农业用水量提供合理的波动区间，主要原因是分数阶灰色模型新信息利用的功能以及加权马尔可夫链的修正作用。一方面，分数阶灰色模型相较传统灰色模型具有新信息优先、预测扰动小的优势，在模拟预测中具有更高的精度，这与魏明奎等[22]的研究结果一致；另一方面，加权马尔可夫链能够对未来误差状态进行合理的预测，并在修正预测值的同时提供预测区间，蒋峰等[23]也证明了这一结论。

虽然新模型预测精度得到了较大改善，但本研究仍存在一些不足之处。首先，本研究选取的研究区数量较少，还需要在我国其他地区进行进一步的适用性研究。此外，除了本研究提出的区间预测方法外，以核密度估计法、分位数回归法等为基础的区间预测方法被广泛应用于风电功率、光伏出力预测等领域[24-25]，而较少应用于农业用水预测领域，农业用水的区间预测有待进一步深入研究。

5 结 论

1）DWT-FGM(1,1)-ARMA组合模型能够有效消除原始用水序列的波动性，且分数阶灰色模型FGM(1,1)和ARMA模型相结合，在充分利用序列的新信息同时提高了模型对于序列随机成分的捕捉能力，能够有效提高模型的预测效果。

2）DWT-WFGM(1,1)-ARMA组合模型采用加权马尔可夫链对DWT-FGM(1,1)-ARMA模型预测结果进行修正，能够进一步利用残差数据中的有效信息，提高模型的预测性能。且相较传统预测模型可以在短期内同时对未来农业用水量和用水区间进行有效预测，为区域农业用水预测工作提供新的思路。

3）在采用加权马尔可夫链对误差状态区间进行预测的过程中，误差状态预测的不确定性随着预测年限的增长不断增大，进而导致长期预测的结果失准。经检验，加权马尔可夫链在短期（3 a）内修正预测的准确率较高，可以为短期农业用水量预测提供更加可靠的依据。

4）在历史样本较小的条件下，应用DWT-WFGM(1,1)-ARMA组合模型对陕西省和内蒙古自治区农业用水量预测的平均绝对百分比误差分别为1.25%和1.01%，相比其他模型预测精度最高，是一种有效的农业用水预测方法。

[1] 李保国, 黄峰. 1998—2007年中国农业用水分析[J]. 水科学进展, 2010, 21(4): 575-583.

LI Baoguo, HUANG Feng. Trends in China’s agricultural water use during recent decade using the green and blue water approach[J]. Advances in Water Science, 2010, 21(4): 575-583.

[2] 崔丙健, 高峰, 胡超, 等. 非常规水资源农业利用现状及研究进展[J]. 灌溉排水学报, 2019, 38(7): 60-68.

CUI Bingjian, GAO Feng, HU Chao, et al. The use of brackish and reclaimed waste water in agriculture: a review[J]. Journal of Irrigation and Drainage, 2019, 38(7): 60-68.

[3] 赵桂生, 张海文, 刘爱军, 等.基于等维递补灰色GM(1,1)模型的我国农业灌溉用水预测分析[J]. 数学的实践与认识, 2018, 48(4): 299-304.

ZHAO Guisheng, ZHANG Haiwen, LIU Aijun, et al. Prediction and analysis of agricultural irrigation water in China based on grey GM (1, 1) model with equal dimension[J]. Mathematics in Practice and Theory, 2018, 48(4): 299-304.

[4] 黄修桥, 康绍忠, 王景雷. 灌溉用水需求预测方法初步研究[J]. 灌溉排水学报, 2004, 23(4): 11-15.

HUANG Xiuqiao, KANG Shaozhong, WANG Jinglei. A preliminary study on predicting method for the demand of irrigation water resource [J]. Journal of Irrigation and Drainage, 2004, 23(4): 11-15.

[5] 刘迪, 胡彩虹, 吴泽宁. 基于定额定量分析的农业用水需求预测研究[J]. 灌溉排水学报, 2008, 27(6): 88-91.

LIU Di, HU Caihong, WU Zening. Predicting method for demand of agriculture water based on quantitative analysis[J]. Journal of Irrigation and Drainage, 2008, 27(6): 88-91.

[6] 白鹏, 龙秋波. 3种用水量预测方法在京津冀地区的适用性比较[J]. 水资源保护, 2021, 37(2): 102-107.

BAI Peng, LONG Qiubo. Applicability comparison of three water consumption prediction methods in Beijing-Tianjin-Hebei region[J]. Water Resources Protection, 2021, 37(2): 102-107.

[7] ZHANG X Q, YUE M L, YAO Y, et al. Regional annual water consumption forecast model[J]. Desalination and Water Treatment, 2018, 114: 51-60.

[8] LIU S F, TAO L Y, XIE N M, et al. On the new model system and framework of grey system theory[J]. Journal of Grey System, 2016, 28(1): 1-15.

[9] 崔东文, 包艳飞. 基于人工生态系统优化算法的组合生长需水预测模型[J]. 水资源保护, 2020, 36(6): 122-130.

CUI Dongwen, BAO Yanfei. Combined growth water demand forecasting model based on artificial ecosystem optimization algorithm[J]. Water Resources Protection, 2020, 36(6): 122-130.

[10] 佟长福, 史海滨, 包小庆, 等. 基于小波分析理论组合模型的农业需水量预测[J]. 农业工程学报, 2011, 27(5): 93-98.

TONG Changfu, SHI Haibin, BAO Xiaoqing, et al. Application of a combined model based on wavelet analysis for predicting crop water requirement[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(5): 93-98.

[11] 邓权龙, 蒋仲安, 韩硕. 基于小波分析与GM(1,1)-ARMA(p,q)组合的矿井防尘用水量预测[J]. 矿业安全与环保, 2018, 45(4): 75-79.

DENG Quanlong, JIANG Zhongan, HAN Shuo. Prediction of coal mine dustproof water consumption based on the combination of wavelet analysis and GM (1, 1)-ARMA (p, q)[J]. Mining Safety & Environmental Protection, 2018, 45(4): 75-79.

[12] TIWARI M K, ADAMOWSKI J F. Medium-term urban water demand forecasting with limited data using an ensemble wavelet–bootstrap machine-learning approach[J]. Journal of Water Resources Planning and Management, 2015, 141(2): 04 014 053.

[13] 吴利丰, 刘思峰, 刘健. 灰色GM(1,1)分数阶累积模型及其稳定性[J]. 控制与决策, 2014, 29(5): 919-924.

WU Lifeng, LIU Sifeng, LIU Jian. GM(1,1) model based on fractional order accumulating method and its Stability[J]. Control and Decision, 2014, 29(5): 919-924.

[14] 王俊芳, 罗党. 振荡序列的分数阶离散GM(1,1)幂模型及其应用[J]. 控制与决策, 2017, 32(1): 176-180.

WANG Junfang, LUO Dang. Fractional order discrete grey GM(1,1) power model based on oscillation sequences and its application[J]. Control and Decision, 2017, 32(1): 176-180.

[15] 潘显俊, 张炜, 赵田, 等. 分数阶离散灰色模型及其在备件需求预测中的应用[J]. 兵工学报, 2017, 38(4): 785-792.

PAN Xianjun, ZHANG Wei, ZHAO Tian, et al. Fractional order discrete grey model and its application in spare parts demand forecasting[J]. Acta Armamentarii, 2017, 38(4): 785-792.

[16] MA X, MEI X, WU W Q, et al. A novel fractional time delayed grey model with Grey Wolf Optimizer and its applications in forecasting the natural gas and coal consumption in Chongqing China[J]. Energy, 2019, 178: 487-507.

[17] WU L, LI N, ZHAO T. Using the seasonal FGM(1, 1) model to predict the air quality indicators in Xingtai and Handan[J]. Environmental Science and Pollution Research, 2019, 26(14): 14 683-14 688.

[18] 郝丽娜, 粟晓玲, 黄巧玲. 基于小波广义回归神经网络耦合模型的月径流预测[J]. 水力发电学报, 2016, 35(5): 47-54.

HAO Lina, SU Xiaoling, HUANG Qiaoling. Monthly runoff prediction using wavelet transform and generalized regression neural network model[J]. Journal of Hydroelectric Engineering, 2016, 35(5): 47-54.

[19] 赵建忠, 徐廷学, 葛先军, 等. 基于小波变换和GM-ARMA的导弹备件消耗预测[J]. 北京航空航天大学学报, 2013, 39(4): 553-558.

ZHAO Jianzhong, XU Tingxue, GE Xianjun, et al. Consumption forecasting of missile spare parts based on wavelet transform and revised GM-ARMA model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 553-558.

[20] LI F, LIU S F, YAO L G, et al. Grey system model with the fractional order accumulation [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7): 1 775-1 785.

[21] 季玉琦, 耿光飞, 温渤婴, 等. 基于最优分割法的含DG配电网动态无功优化[J]. 电网技术, 2017, 41(8): 2 585-2 592.

JI Yuqi, GENG Guangfei, WEN Boying, et al. Dynamic reactive power optimization in distribution network with DG based on optimal partition[J]. Power System Technology, 2017, 41(8): 2 585-2 592.

[22] 魏明奎, 周全, 蔡绍荣, 等. 基于BFGS-FA优化的分数阶灰色模型的中长期负荷预测[J]. 广西大学学报(自然科学版), 2020, 45(2): 270-276．

WEI Mingkui, ZHOU Quan, CAI Shaorong, et al. Mid-Long term Load forecasting based on fractional gray model optimized by BFGS-FA[J]. Journal of Guangxi University (Natural Science Edition), 2020, 45(2): 270-276.

[23] 蒋峰, 王宗耀, 张鹏. 基于灰色-加权马尔可夫链的光伏发电量预测[J]. 电力系统保护与控制, 2019, 47(15): 55-60.

JIANG Feng, WANG Zongyao, ZHANG Peng. Forecasting power generation of solar photovoltaic system based on the combination of grey model and weighted Markov chain[J]. Power System Protection and Control, 2019, 47(15): 55-60.

[24] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1 201-1 217.

LAI Changwei, LI Jinghua, CHEN Bo, et al. Review of photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1 201-1 217.

[25] 杨茂, 董昊. 基于数值天气预报风速和蒙特卡洛法的短期风电功率区间预测[J]. 电力系统自动化, 2021, 45(5): 79-85.

YANG Mao, DONG Hao. Short-term wind power interval prediction based on wind speed of numerical weather prediction and Monte Carlo method[J]. Automation of Electric Power Systems, 2021, 45(5): 79-85.

Predicting Agricultural Water Demand Using the DWT-WFGM (1,1)-ARMA Model

WANG Guanzhi1,2, SU Xiaoling1,2*, ZHANG Te1,2, JIANG Tianliang1,2, CHU Jiangdong1,2

(1.College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China; 2. Key Laboratory of Agricultural Soil and Water Engineering in Arid Area of Ministry of Education, Northwest A&F University, Yangling 712100, China)

【】The increased demand for water due to economic development coupled with dwindling water supply is the double whammy facing most provinces in north China. Given agriculture is the biggest water use sector, understanding the change in agricultural water demand is critical to improving water resources management. The purpose of this paper is to present a new method to estimate agricultural water use changes at provincial scale in the north of China.【】The proposed method was based on discrete wavelet transform (DWT), fractional-order grey model (FGM(1,1)), weighted Markov Chain (WMC), and autoregressive moving average (ARMA) model. The time series of agricultural water demand was firstly decomposed into approximate series and detailed series, respectively, using DWT. FGM(1,1) was then used to describe the approximate series, with the errors corrected by WMC. The Fisher optimal segmentation method was used to divide the state intervals of the predicted errors, and the state intervals were predicted using a probability transfer matrix. The predicted intervals and values of the approximate series were obtained from the boundary values and median of the predicted error state intervals. In comparison, the detailed series were predicted using the ARMA model based on the Akaike Information Criteria. These were used to predict the agricultural water demand and its intervals. We applied the models to agricultural water demand in Shaanxi and Inner Mongolia provinces, with data measured from 2002 to 2015 used to train the model and those measured from 2016 to 2019 to validate the model. We compared the results calculated from the proposed model with those estimated from the traditional GM (1,1), DWT- GM(1,1)-ARMA, and DWT-FGM(1,1)-ARMA models.【】The average absolute error of the proposed model for the two provinces was 1.25% and 1.01%, respectively, much less than those given rise to by other models. The predicted agricultural water demand intervals showed that after correction by WMC, the model provided reliable short-term fluctuation intervals in agricultural water demand in both provinces.【】The proposed model for predicting agricultural water demand at provincial scale was accurate and robust. It can also predict the intervals which describe the short-term fluctuation in agricultural water demand. The model has an implication in helping improve water management and developing sustainable agriculture.

agricultural water consumption; fractional-order grey model; weighted Markov chains; discrete wavelet transform; predicted intervals

TV213.4

A

10.13522/j.cnki.ggps.2021177

王冠智, 粟晓玲, 张特, 等. 基于DWT-WFGM(1,1)-ARMA组合模型的农业用水量预测[J]. 灌溉排水学报, 2021, 40(11): 106-114.

WANG Guanzhi, SU Xiaoling, ZHANG Te, et al. Predicting Agricultural Water Demand Using the DWT-WFGM (1,1)-ARMA Model[J]. Journal of Irrigation and Drainage, 2021, 40(11): 106-114.

1672 - 3317（2021）11 - 0106 - 09

2021-04-28

国家自然科学基金项目（52079111）；“十三五”国家重点研发计划项目（2016YFC0401306）

王冠智（1997-），男，山东日照人。硕士研究生，主要从事用水预测研究。E-mail: guanzhiwang@163.com

粟晓玲（1968-），女，四川开江人。教授，博士生导师，主要从事水文模拟及水资源优化研究。E-mail: xiaolingsu@nwafu.edu.cn

责任编辑：陆红飞