发动机冷却风扇气动噪声数值仿真预测与分析

黄 毅，龙书成，李 智，常文瑞，王伟江

（广州汽车集团股份有限公司 汽车工程研究院，广州 511434）

在汽车发动机热负荷和电器设备功率需求日益增大的趋势下，对发动机冷却风扇转速要求不断提高，另一方面，用户对车内舒适性的要求也在提高，有关法规对NVH的要求也越来越苛刻，冷却风扇是整车怠速工况下贡献较大的噪声源部件之一[1－2]，对其噪声的准确预测和控制至关重要。冷却风扇工作时，产生的噪声类型主要包括叶片气动噪声、电机电磁噪声和电刷及轴承等旋转摩擦产生的机械噪声[3－4]，其中风扇叶片产生的气动噪声在车内最容易被用户感知，是影响用户对怠速车内声学环境舒适性评价的重要指标[5]。因此，找到准确高效的冷却风扇气动噪声仿真预测方法十分重要，也是进一步实现冷却风扇气动噪声仿真优化控制的必要前提。

国内外学者对风扇气动噪声的研究主要在气动噪声的形成机理、试验分析和数值预测仿真方法三方面展开。气动噪声的研究始于Lighthill的喷气四极 子 噪 声，又 经 过Curle、Ffowcs - Williams 和Hawkings发展建立了基于声类比FW-H方程的气动声学理论体系[6-7]。张亚东等和万剑锋等通过试验研究旋转风扇气动噪声，分析了风扇阶次噪声特性，揭示了风扇气动噪声的指向性规律[8-9]。蒋炎坤等、韩宝坤等和王嘉冰等采用LES大涡模拟和FW-H声学模型对风扇气动噪声特性进行仿真预测，预测结果表明风扇气动噪声主要集中在中低频，气动噪声大小与涡流强度有直接关系[10-11,14]。

本文在采用Star CCM+软件进行包含消声室的冷却风扇CFD建模基础上，结合FW-H声学方程，分别采用DES分离涡和LES大涡模拟预测气动噪声，通过风扇噪声测试对比分析了两种预测方法对于离散阶次噪声、宽频涡流噪声和总声压级的仿真预测误差，同时分析了两种方法对不同噪声源预测精度具有差异的原因。文中采用的冷却风扇气动噪声数值预测流程方法可为冷却风扇的NVH 开发和优化控制提供有效指导，也可为后续整车状态下风扇气动噪声的CFD 建模及气动噪声仿真预测提供有效参考。

1 噪声数值预测方法及CFD 模型建立

1.1 数值预测流程方法

冷却风扇的气动噪声主要由叶片的离散阶次噪声和宽频涡流噪声构成[10]，根据声类比理论，可由FW-H方程[12-13]表示为：

式中：p′为压力脉动，p′=p-p0；c0为声速；ui为速度分量；Tij为Lighthill 张量分量；pij为应力张量分量；δ(f)为Diracdelta 函数；ρ0为未受扰动时流体密度。式中右侧3 项分别为四极子、偶极子、单极子噪声源。

由于风扇气动噪声分析中假设风扇总成表面为刚性，单极子噪声源近似为零。文中风扇叶片直径为400 mm，高低档转速分别为1 800 r/min 和2 500 r/min，马赫数Ma最大为0.16，雷诺数高达104级，流体表现为不可压缩湍流状态。根据文献[14]的结论，偶极子和四极子噪声强度大小与马赫数Ma的关系为：

式中：ID为偶极子噪声源强度；IQ为四极子噪声强度；u为流体速度。计算可知，四极子噪声强度仅为偶极子的2.5%，因此四极子噪声可以忽略不计[15]。

在STAR CCM+中先采用RANS SST K-Omega湍流方程模型求解风扇CFD流场定常解，然后分别采用LES大涡和DES分离涡模拟求非定常解，其中LES 模拟直接求解大尺度涡，对小尺度涡采用亚格子模拟求解，采用DES 分离涡模拟时在壁面区采用RANS 方程，而在核心区采用LES 大涡模拟[16]，最后采用FW-H 声类比方程模拟求解远场噪声，整个风扇气动噪声数值预测方法流程如图1所示。

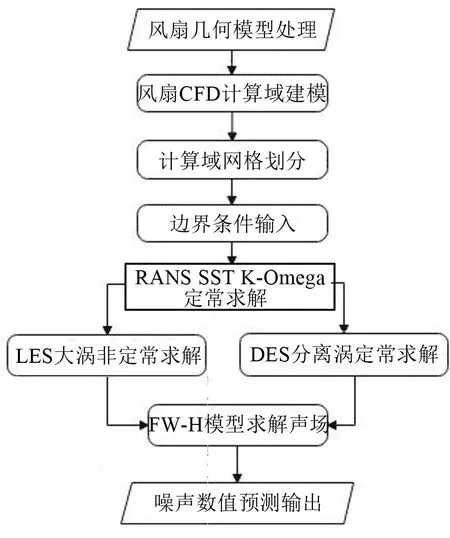
图1 风扇气动噪声预测方法流程图

1.2 风扇气动噪声CFD模型建立

（1）风扇气动噪声计算域模型建立

冷却风扇总成主要性能及尺寸参数如表1 所示。将对CFD 计算影响较小的几何特征简化处理后的风扇模型导入STAR CCM+中，同时为模拟风扇在消声室的工作环境，在风扇外围建立4 m×3 m×2 m的立方体计算域。

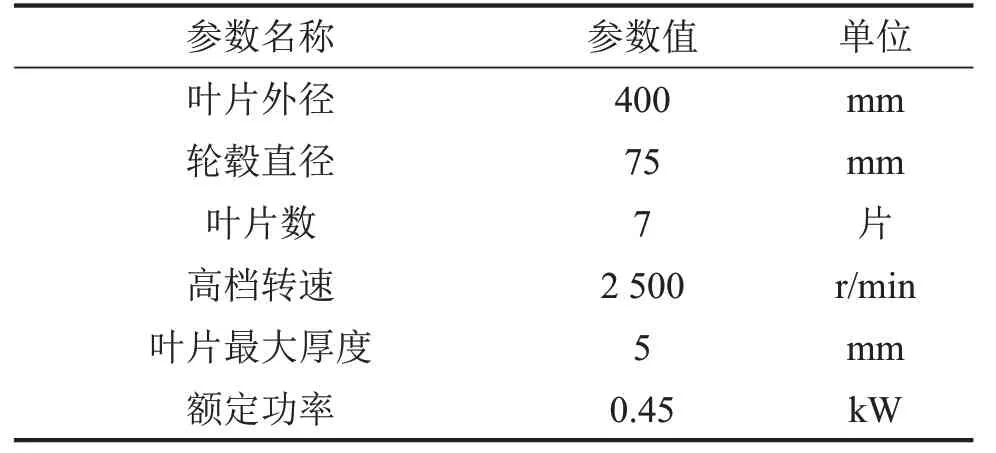
表1 风扇主要参数

（2）计算域网格划分

整个计算域划分为风扇旋转区、风扇罩壳外加密区和消声室区，划分结果如表2所示。

表2 计算域各块网格基本尺寸及数量分布

其中壁面区采用3 层棱柱层网格，棱柱层增长率为1.1，整个CFD计算域采用Trimmer Mesher类型网格，划分好网格后的计算域剖面如图2所示。

图2 计算域网格剖面图

（3）边界条件处理

分别进行风扇低档（1 800 r/min）和高档（2 500 r/min）运行工况的CFD 计算，其中边界条件设置如表3所示。

表3 计算域边界条件设置

2 定常数值计算及结果分析

2.1 定常计算物理模型

在Star CCM+中定常求解的物理模型设置如表4所示。文中同时对风扇高档(2 500 r/min)工况和低档(1 800 r/min)工况分别进行CFD 流场和噪声仿真计算，但由于篇幅限制，定常计算仅以风扇高档2 500 r/min 工况为例分析，风扇高低档噪声相关仿真计算和测试结果都会在非定常分析中呈现。

表4 定常计算物理模型设置

进行定常计算时在风扇中心前后端水平距离1 m 处分别设置压力监测点，其中风扇2 500 r/min 运行工况的压力监测随迭代变化情况如图3所示。可知定常压力计算结果在920 步时已达到充分稳定收敛。

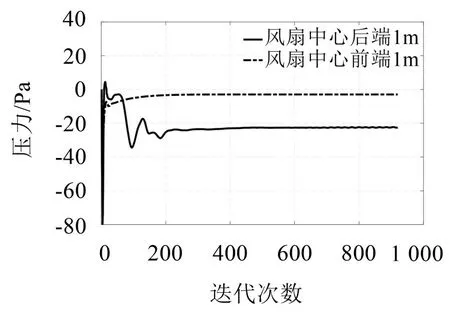
图3 定常计算中监测点压力迭代变化情况

2.2 定常计算结果分析

图4为风扇2 500 r/min运行工况的定常计算所得速度场，由图可知，整个计算域内最大速度达到55.0 m/s，最大风速主要分布在风扇叶尖边缘，与理论推算结果一致，可作为后续非定常计算的初始解。

图4 定常计算所得速度场

风扇叶片表面的涡流压力脉动是形成偶极子噪声源的主要原因，而这种压力脉动的强烈程度可以用涡流湍动能衡量[17-18]，2 500 r/min运行工况下的涡流强度、湍动能仿真分布和噪声源测试结果如图5所示。

图5(a)所示的涡流强度分布仿真结果表明在叶片下游中部附近涡流强度最大，这种涡流会加剧叶片中部区域的压力脉动，形成较大的湍动能，从而产生较大的偶极子噪声源；图5(b)所示的湍动能仿真分布结果表明湍动能最大区域也集中在风扇叶片前缘中部至叶尖位置，这与图5(c)所示的噪声源试验识别结果一致，表明该定常数值预测模型能够比较准确地识别噪声源分布位置。

图5 基于数值仿真与试验噪声源识别对比

3 非定常数值计算及结果分析

3.1 非定常计算物理模型

以定常计算结果作为初始解进行非定常计算，非定常求解时物理模型设置如表5 所示，其中湍流模型分别采用LES大涡和DES分离涡模拟。

表5 非定常计算物理模型设置

进行非定常计算时设置采样时间步长time step=10-4s，内部迭代次数为20 次，根据Nyquist 采样定理，采样频率为fs=10 kHz，可以分析5 kHz内的声压级信息。采样时间t要大于流动变化特征的5 倍以上，非定常的流场特征才能充分发展，采样时间根据斯特劳哈尔数St（Strouhal Number）确定,其定义为[12]：

式中：f为特征频率；d为特征长度，为结构特征在流体流动方向上的投影宽度；v为流体速度。高雷诺数下St取值范围[10]为0.14～0.2，一般取为0.18，根据定常计算结果，流体最大速度为55.0 m/s，特征长度主要考虑叶片厚度、叶片宽度、风扇罩壳支撑筋的宽度和风扇罩壳宽度，其中罩壳宽度最大为680 mm，代入定义式可知流场主要的最小特征频率约为16 Hz，特征周期为0.05 s，采样时间t设置为0.35 s，是整个流场特征周期的7倍，流动特征足以充分发展。

3.2 非定常计算结果分析

在距风扇中心前端面1 m处设立压力脉动监测点，分别输出高低档工况非定常计算完成后FW-H声学模型监测点时域压力脉动如图6所示。由图可知，采用LES和DES模拟求解的监测点处压力脉动都呈现出一定的周期特征，但基于LES 求解的压力波动幅值普遍更大，并且含有更多的尖峰细节成分特征。

图6 风扇中心前端1 m处时域压力脉动仿真对比

在半消声室内采用LMS 数采分别进行风扇高档（2 500 r/min）和低档（1 800 r/min）运行工况下的噪声测试，测试环境如图7所示，消声室空间大小与仿真计算域相当，消声室背景噪声为20.3 dB(A)，风扇用橡胶绳悬挂在位于消声室中间的支架上，麦克风置于风扇中心前端1 m 处，采样频率设置为10 kHz。

图7 半消声室冷却风扇噪声测试环境

对测试和仿真所得的噪声时域数据进行A计权FFT 分析，频率分辨率为3.3 Hz，仿真与测试频谱对比如图8所示，由图可知，高低档两种工况下的基于DES和LES仿真模拟都能够捕捉到叶片前3阶离散阶次噪声峰值特征，而LES 模拟对宽频涡流噪声的预测结果明显大于DES模拟，更逼近测试值。

图8 风扇前端1 m处声压级频谱测试与仿真对比

叶片阶次噪声和总声压级仿真测试误差统计如表6所示。可知两种工况下基于LES仿真的总声压级相对误差都控制在为5%以下，而基于DES 仿真值误差都在8%以上，基于LES 仿真的总声压级值精度更高。而对于叶片前3 阶离散阶次噪声而言，两种工况下DES 仿真值相对误差都控制在6 %以下，而LES仿真值误差都在6%以上，尤其在风扇低档工况下最大误差达到18.9%，仿真误差较DES 模拟更大。

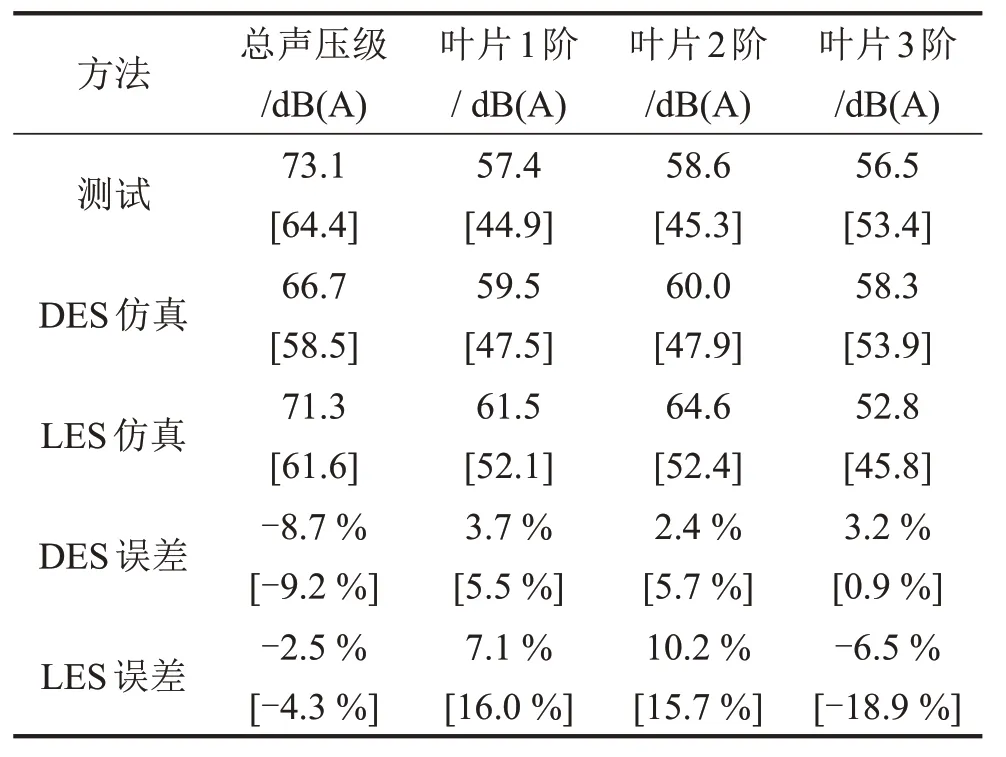
表6 总声压级与叶片阶次噪声仿真测试误差

以风扇高档（2 500 r/min）仿真工况为例，分别采用LES 和DES 模拟对在0.2 s 时风扇叶片X 截面附近的涡流强度进行非定常计算，结果如图9所示。对比分析可知，由于对整个计算域采用大涡模型，LES模拟对于风扇叶片附近涡流强度的梯度计算更精细，更能准确地捕捉到叶片附近的不同强度的无序涡流如图9(a)所示，从而使得LES 大涡模拟更能够准确预测因无序涡流压力脉动产生的宽频噪声源，而由于在壁面区附近采用RANS雷诺平均方程，在壁面区从时间和空间上进行平均化处理，将小尺度的涡平均化，减弱了无序涡流对叶片周期性切割空气所产生的压力脉动所形成的离散叶片阶次噪声影响，使得叶片附近基于DES 分离涡模拟计算所得的涡流强度分布梯度更小，分布更均匀，如图9(b)所示，因此DES 模拟更能准确地预测出叶片周期性离散阶次噪声，这与仿真测试结果一致。

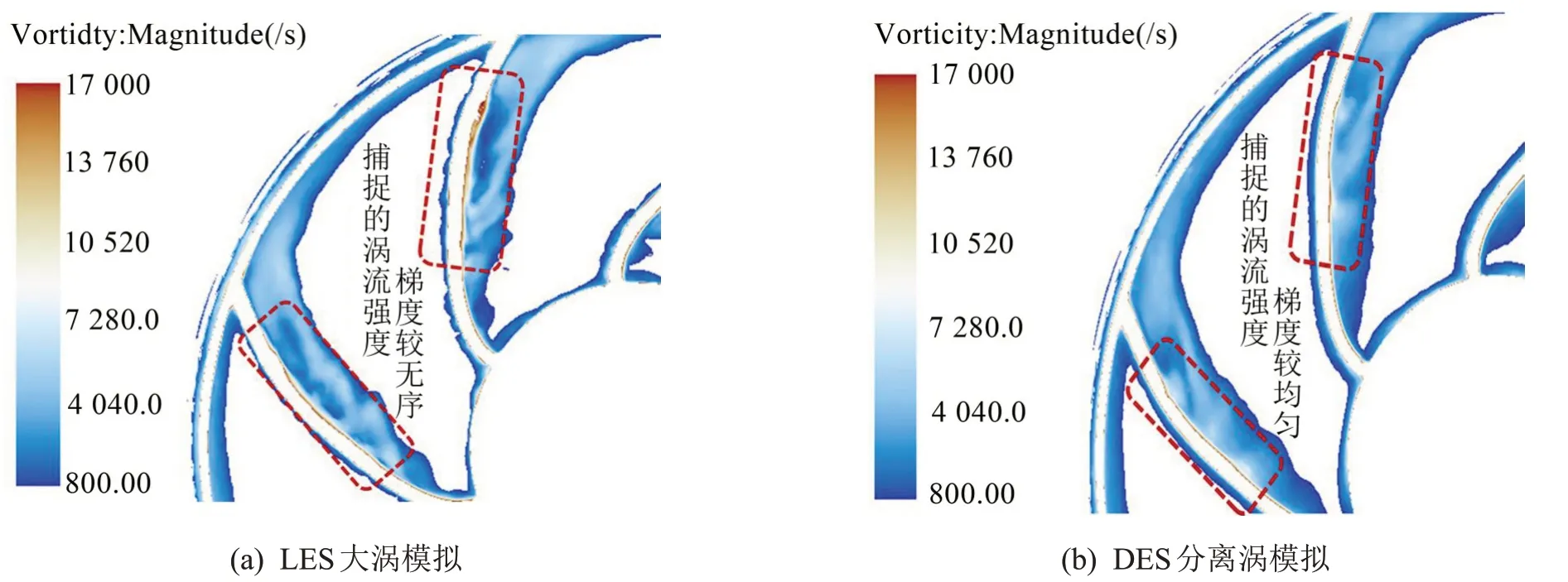
图9 高档（2 500 r/min）工况0.2 s时叶片X截面涡流强度

4 结语

针对发动机冷却风扇气动噪声问题，在建立包含消声室的风扇CFD 模型的基础上，结合FW-H 声类比方程，分别采用DES分离涡和LES大涡模拟仿真预测气动噪声，并将仿真预测值与噪声试验结果对比分析，得到以下结论：

（1）DES分离涡模型中在叶片壁面附近的平均化处理能够有效降低无序涡流对叶片周期性切割空气所产生的压力脉动影响，较LES 大涡模拟更能准确地预测叶片周期性离散阶次噪声。

（2）LES 大涡模拟更能够准确捕捉叶片附近不断形成及消散涡流所产生的无序宽频脉动压力，对宽频涡流噪声的仿真预测大涡模拟误差更小。

（3）由于风扇高速运转时叶片附近的涡流强度大，而且尺度分布广，使得宽频涡流噪声具有很大的噪声源贡献量占比，虽然DES 对离散阶次噪声预测更准，但对宽频噪声源仿真误差较大，因此基于LES大涡模拟预测的总声压级误差更小。