基于展向波纹结构受电弓杆件减阻降噪研究

张长亮，刘海涛，周 新，杨春辉，肖 乾

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

随着我国高速列车的不断提速，由列车产生的气动噪声将逐渐超越轮轨噪声成为主导。在未来，更高速等级的高速列车在噪声方面的主要问题将会是气动噪声问题。

受电弓位于列车顶部，由多个杆件组成，在高速气流中会产生显著的气动噪声。由于列车顶部的防护隔离手段有限，受电弓气动噪声对周围环境的噪声污染更为显著。国外学者较早就开展了受电弓降噪研究，并提出了众多的改进方案。受益于国家高铁发展战略的影响，近年来我国针对高速列车受电弓气动特性、气动噪声领域的研究也得到了快速发展。张亚东等[1]在风洞实验中模拟分析了高速列车以250 km/h 运行时受电弓气动噪声特性，得出受电弓产生的气动噪声集中在迎风侧区域的弓头、底架、绝缘子等部件中的结论。刘海涛等[2]基于仿生学设计了6 种杆件结构，发现锯齿结构的椭圆外形结构杆件对于降低受电弓的气动噪声有显著效果。侍荣春等[3]对受电弓杆件建立类高尔夫圆柱杆件的气动噪声模型，研究结果表明圆柱表面球缺型凹坑设计使得圆柱杆件升力、阻力系数出现较高频率的波动，远场气动噪声高频部分的声压级变大。Cao 等[4]探讨了鸽子羽毛的降噪性能，并在受电弓杆件表面进行了非对称截面杆件的仿生设计，优化后的非对称截面杆件尾部涡流的脱落得到有效控制，优化后的模型在高频区域受电弓气动噪声值明显降低。IKEDA 等[5－6]沿杆件轴向方向将受电弓弓角进行了打孔优化处理，在具有连续通孔受电弓弓角的结构中，连续射流与剪切层之间的相互作用会引起明显的窄带噪声。Bearman和Owen[7]在受电弓杆件迎风面和背风面上引入了展向波纹，发现在迎风面上展向波纹的波长和振幅对减阻和抑制旋涡脱落有重要作用，但在背风面上减阻效果影响不大。Darekar和Sherwin[8]通过对前后表面均具有展向波纹的直方杆进行数值模拟，证实了展向波纹对减阻的影响。Lam 和Lin[9]在沿翼展方向引入正弦变化的横截面，将波纹度的概念扩展到圆柱体，发现圆柱体模型的平均力系数和波动力系数显著降低。展向波纹结构对于降低气动噪声具有一定效果，但受电弓弓头的展向波纹结构参数与降噪性能的关系还缺乏深入研究。

在本研究中，将展向波纹结构引入到弓头杆件的迎风面和背风面，基于波长和波纹幅度两个参数建立8组受电弓弓头展向波纹结构模型。弓头展向波纹结构参数优化设计重点在研究波长和波纹幅度对模型气动特性的影响，通过流体计算软件FLUENT进行稳态和瞬态计算求解，采用标准k-ε模型来计算稳态流场，在此基础上通过大涡模拟计算瞬态流场，基于气动噪声混合计算方法，将瞬态流场计算结果通过积分插值映射到声学网格上，并通过计算获取气动噪声声源及传播过程。通过对考察范围内的弓头展向波纹结构参数进行优化分析，获得较优性能的展向波纹结构参数模型。

1 计算理论及方法

1.1 流体流动的控制方程

对受电弓弓头展向波纹结构模型的周围流场进行数值仿真，模拟高速列车60 m/s的运行速度，由于气流流速小于0.3 倍马赫数，可认定空气不可压缩。完整的三维N-S方程守恒形式如式（1）所示。

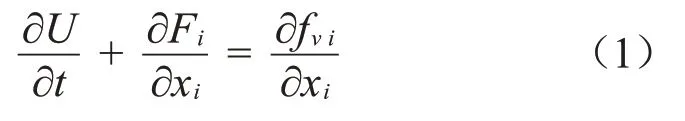
式中：U、F的表达式如式（2）所示。

式中：ρ、E、H、p、T分别为密度、总能、总焓、压强和温度；δij为克罗尼柯尔符号；μ,λ,κ分别为第一、第二黏性系数和热传导系数；τij=为黏性应力张量。

1.2 宽频噪声模型

本研究中采用宽频噪声模型对展向波纹结构杆件进行稳态计算求解。宽频带噪声模型声功率计算公式如式（3）所示。其中：u是湍流速度，l是湍流特征尺度，c0是声速，α为模型常数。

对于湍动能k和湍动能耗散率ε，式（3）可以改写成式（4）形式。

其中：Mt=模型中设置αε=0.1。

气动噪声声功率级如式（5）所示。

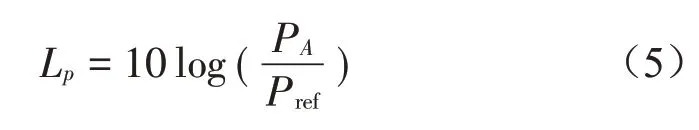
式中：Pref是参考声压，取10-12W/m3。

2 弓头展向波纹结构研究方法

2.1 弓头展向波纹结构模型参数化建模

建立弓头展向波纹结构波纹杆件模型，典型的高速列车受电弓上的接触条横截面宽度和高度几乎相同，因此杆件的横截面实际上被近似为正方形，如图1所示，其中D=0.04 m为固定值，ω是波峰到波谷的振幅，λ为波长，上游最远的横截面称为“峰”，下游最远的横截面称为“谷”。选择无量纲波长λ/D为2 和4，无量纲波纹度ω/D为0.12、0.24、0.36 和0.48。两个参数交叉组合，建立8 组参数化模型，如表1 所示。高速列车在行驶过程中受电弓弓头结构处于无限大且无边界的气流当中，在流场仿真计算中，仅考虑受电弓附近的流场受到扰动，因此对展向波纹结构模型进行局部流场空气域的设计。如图2、表1所示，在（x，y，z）方向上的域大小（Lx，Ly，Lz）分别为20D、75D、40D，将模型紧贴壁面，以防止侧边气流的涡旋造成干扰。

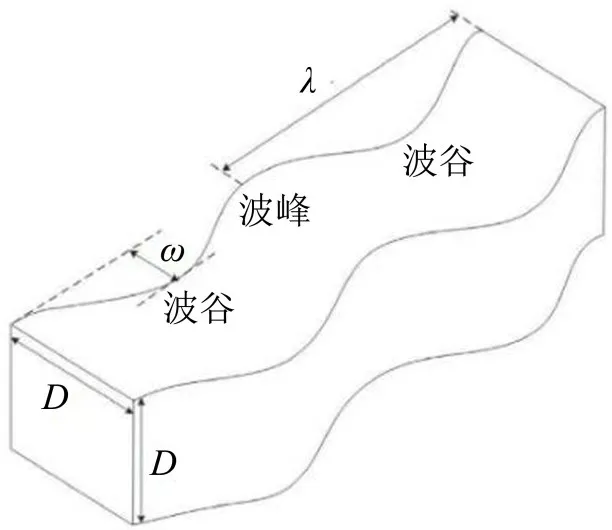
图1 展向波纹模型结构图

图2 展向波纹模型空气域图

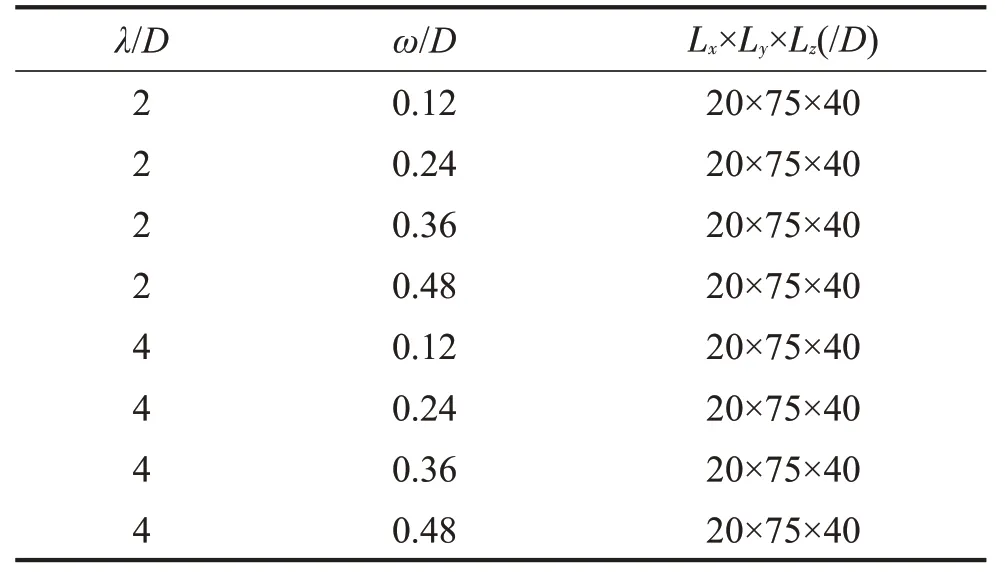
表1 展向波纹结构参数和空气域范围

2.2 弓头展向波纹结构网格划分方法

对展向波纹结构模型进行网格划分，建立有限元模型。为了更好地模拟高速列车运行环境，需要给计算域一个入流速度，以计算域左侧ABCD 面为速度入口，右侧EFGH 面为气流压力出口，ACEG面、BDFH面、ABEF面以及BDFH面为对称边界，弓头展向波纹结构设置为具有固定壁面，如表2所示。为了更好地分析展向波纹结构附近以及尾流区流场变化，分别在模型周围和尾流区域建立两重密度盒子来更好地捕捉流场的变化。进行了网格无关性验证，当网格数从860 万增加至900 万时，数值模拟的结果误差在5%以内，本文计算模型的有限元网格总数量为900万左右，如图3所示。

表2 边界条件

图3 三维有限元网格模型

2.3 弓头展向波纹结构流场后处理方法

弓头展向波纹结构流场计算分为稳态计算和瞬态计算。稳态计算模型的入口边界定义为速度入口，本文以入流速度60 m/s 来模拟仿真列车的运行时速；出口边界定义为压力出口，其中表压为0，速度垂直于入口进入，回流湍流强度和回流湍流黏度比均为1%；噪声模型采用宽频带噪声模型、标准k-ε模型，基于最小二乘单元进行梯度离散，选用2阶迎风的压力离散格式，并选用SIMPLEC 算法进行迭代计算。

采用大涡模拟进行瞬态计算求解，亚格子模型为Wale，压力速度耦合算法采用Couple算法。本文计算分析的时间步长为10-4s，计算500 个时间步长数，每20 个迭代步数输出一个EnSight Case Gold 文件，为提高计算精度采样频率设置为10 000 Hz，本文中分析的最高频率为2 000 Hz。

2.4 弓头展向波纹结构声场后处理方法

ACTRAN 中通过离散傅里叶变换将稳态求解的时域信号转换为频域信号；采用无线元和有限元相结合的方法对模型进行直接频域相应计算；以展向波纹结构模型为中心，以半径R=1.18 m建立180°的极坐标半圆，以1°为间隔建立180个监测点，如图4所示，通过噪声监测点来分析展向波纹结构模型的远场噪声频谱和指向性。

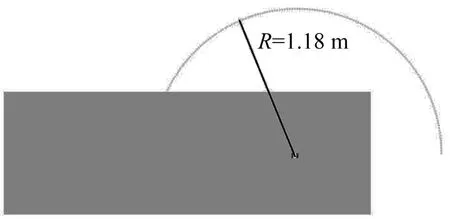
图4 展向波纹结构模型远场噪声监测点

3 弓头展向波纹结构降噪分析

在60 m/s 的来流速度工况下，对不同波纹度ω和波长λ组合的8 组弓头展向波纹结构模型以及直方杆模型的流场、声场模拟计算结果进行分析。图5至图13给出了200 Hz处的噪声云图。

图5 λ/D=2、ω/D=0.12时的展向波纹结构模型噪声云图

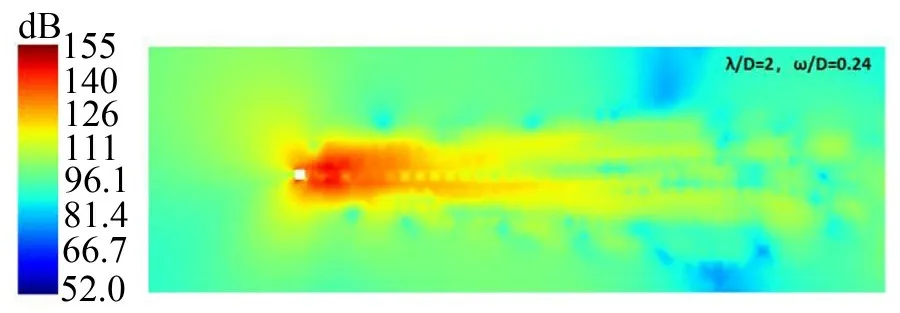
图6 λ/D=2、ω/D=0.24时的展向波纹结构模型噪声云图

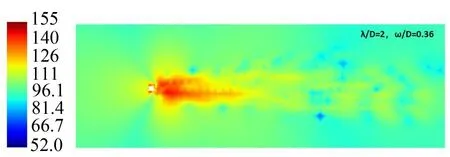
图7 λ/D=2、ω/D=0.36时的展向波纹结构模型噪声云图

图8 λ/D=2、ω/D=0.48时的展向波纹结构模型噪声云图

图9 λ/D=4、ω/D=0.12时的展向波纹结构模型噪声云图

图10 λ/D=4、ω/D=0.24时的展向波纹结构模型噪声云图

图11 λ/D=4、ω/D=0.36时的展向波纹结构模型噪声云图

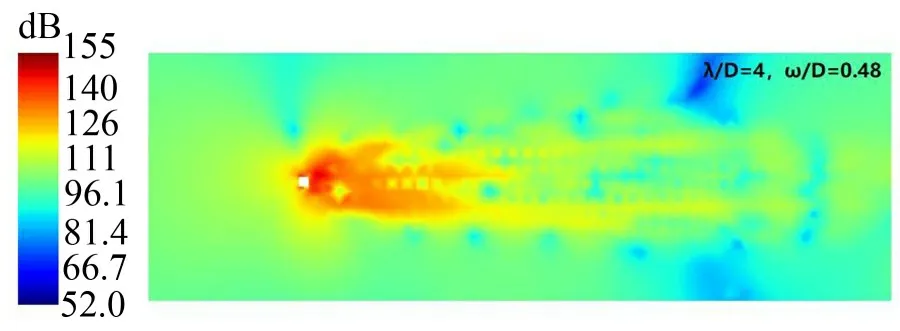
图12 λ/D=4、ω/D=0.48时的展向波纹结构模型噪声云图

图13 直方杆模型噪声云图

由图可以看出，当来流定常以定常速度绕过模型杆件时，弓头展向波纹结构模型杆件和直方杆模型两侧均周期性地脱落出旋转方向相反、排列规则的双列线涡，该现象为典型的卡门涡街现象。直方杆模型在均匀来流速度60 m/s工况下的辐射声压级明显高于展向波纹结构模型；对于λ/D=2、λ/D=4 的展向波纹结构模型，随着波纹幅度ω的增加，辐射的声压级逐级降低，其中λ/D=2、ω/D=0.48 和λ/D=4、ω/D=0.48时的展向波纹结构模型的辐射声压级小于其他参数模型，降噪性能较好；对于ω/D=0.12 时的展向波纹结构模型，随着波长λ的增加，λ/D=2 时的模型杆件辐射声压级小于λ/D=4 时的辐射声压级，降噪性能也更优；对于ω/D=0.24 时的展向波纹结构模型，随着波长的增加，λ/D=2 和λ/D=4 时的模型杆件辐射噪声区别不大；但当ω/D=0.36、ω/D=0.48时，随着波长的增加，λ/D=2 时的模型杆件辐射声压级较λ/D=4时有明显减小趋势。

3.1 弓头展向波纹结构波长的影响

研究弓头展向波纹结构波长λ对气动噪声的影响，对波纹幅度ω为定值的展向波纹结构模型和直方杆模型在R=1.18 m 测点91 处的远场噪声频谱进行分析。由图14 可知，在40 Hz～200 Hz 频率范围内，λ/D=2、ω/D=0.12时展向波纹结构模型较λ/D=4、ω/D=0.12时的展向波纹结构模型和直方杆模型声压级明显降低，在280 Hz～1 400 Hz频率范围内，λ/D=2、ω/D=0.12 和λ/D=4、ω/D=0.12 时的展向波纹结构模型声压级低于直方杆模型；λ/D=2、ω/D=0.12 和λ/D=4、ω/D=0.12时展向波纹结构模型与直方杆模型在200 Hz处均存在峰值声压级，峰值声压级分别为107.24 dB、111.04 dB、109.32 dB；λ/D=2、ω/D=0.12和λ/D=4、ω/D=0.12 时展向波纹结构模型的总声压级为137.75 dB 和137.82 dB，直方杆模型的总声压级为137.32 dB，λ/D=2、ω/D=0.12和λ/D=4、ω/D=0.12时展向波纹结构模型无明显降低气动噪声作用。

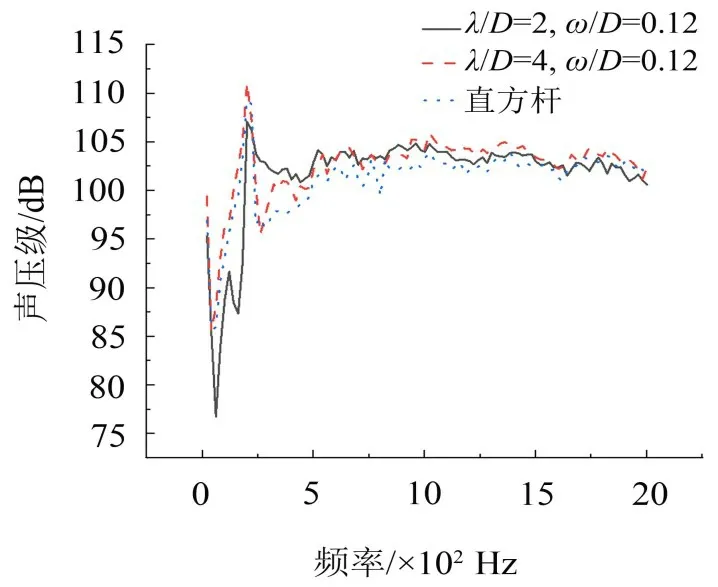
图14 λ/D=2、ω/D=0.12和λ/D=4、ω/D=0.12时展向波纹结构模型和直方杆模型的远场噪声频谱

图15 所示为λ/D=2、ω/D=0.12 和λ/D=4、ω/D=0.12时的展向波纹结构模型和直方杆的远场噪声指向性，直方杆模型的声压级在0°～15°、90°～170°的辐射角范围内均大于λ/D=2、ω/D=0.12和λ/D=4、ω/D=0.12 时的展向波纹结构模型。在15°～75°的辐射角范围内，λ/D=2、ω/D=0.12 时的展向波纹结构模型的声压级小于λ/D=4、ω/D=0.12 时的展向波纹结构模型和直方杆模型。在辐射角165°附近，λ/D=2、ω/D=0.12时的展向波纹结构模型声压级最小。

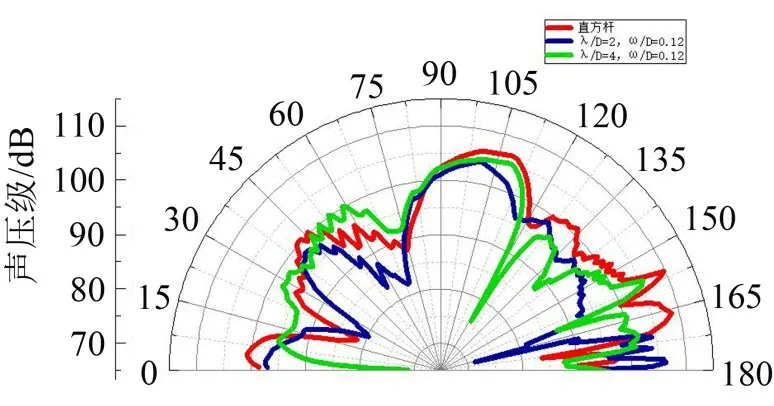
图15 λ/D=2、ω/D=0.12和λ/D=4、ω/D=0.12时展向波纹结构模型和直方杆模型的远场噪声指向性

由图16 可知在160 Hz～2 000 Hz 频率范围内，λ/D=2、ω/D=0.24 时的展向波纹结构模型较λ/D=4、ω/D=0.24时的展向波纹结构模型和直方杆模型声压级明显降低；λ/D=2、ω/D=0.24和λ/D=4、ω/D=0.24时展向波纹结构模型在200 Hz处存在峰值声压级，峰值声压级大小为99.40 dB、103.75 dB；λ/D=2、ω/D=0.24和λ/D=4、ω/D=0.24时的展向波纹结构模型的总声压级为132.54 dB、135.66 dB，λ/D=2、ω/D=0.24 和λ/D=4、ω/D=0.24时的展向波纹结构模型总声压级较直方杆模型降低了4.78 dB、1.66 dB。

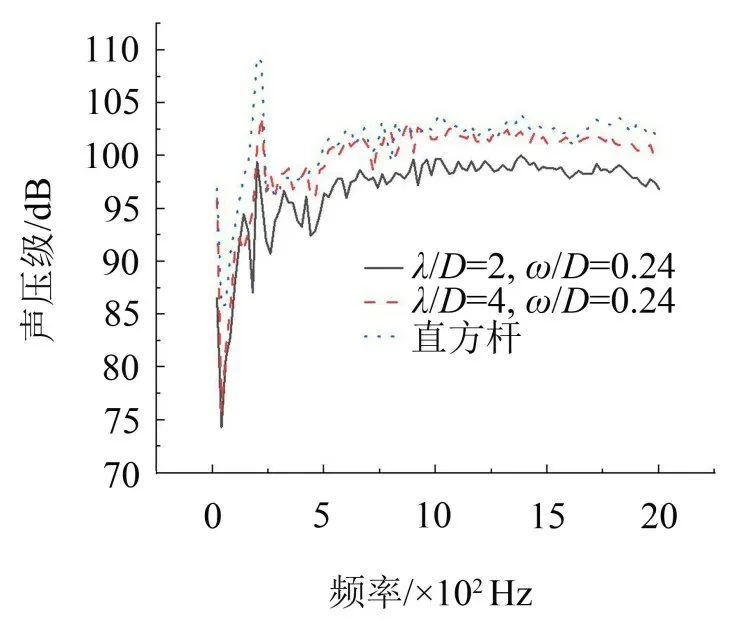
图16 λ/D=2，ω/D=0.24和λ/D=4，ω/D=0.24时展向波纹结构模型和直方杆模型的远场噪声频谱

由图17 可知直方杆模型的声压级在38°～45°、80°～165°的辐射角范围内均大于λ/D=2、ω/D=0.24和λ/D=4、ω/D=0.24时的展向波纹结构模型。在45°～60°的辐射角范围内，λ/D=2、ω/D=0.24时的展向波纹结构模型的声压级小于λ/D=2、ω/D=0.24 时的展向波纹结构模型和直方杆模型。在辐射角55°附近，λ/D=2、ω/D=0.24 时的展向波纹结构模型声压级最小。

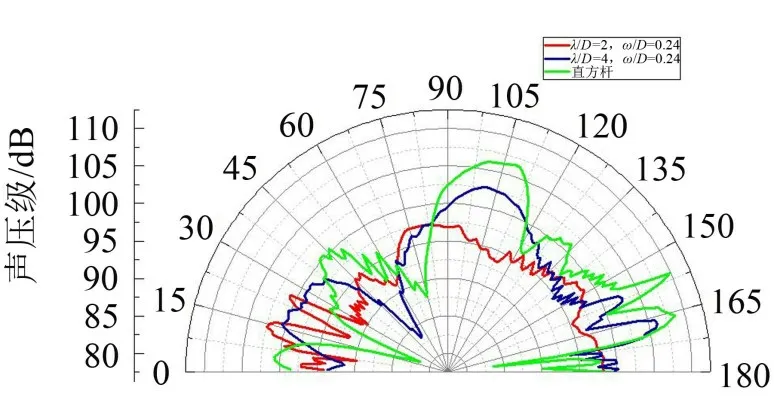
图17 λ/D=2、ω/D=0.24和λ/D=4、ω/D=0.24时展向波纹结构模型和直方杆模型的远场噪声指向性

从图18可以看出在260 Hz～2 000 Hz频率范围内，λ/D=2、ω/D=0.36时的展向波纹结构模型较λ/D=4、ω/D=0.36时的展向波纹结构模型和直方杆模型声压级明显降低；在40 Hz～120 Hz频率范围内，λ/D=4、ω/D=0.36 时的展向波纹结构模型较λ/D=2、ω/D=0.36时的展向波纹结构模型和直方杆模型声压级有所降低；λ/D=4、ω/D=0.36 时的展向波纹结构模型在200 Hz 处仍存在峰值声压级，峰值声压级为102.90 dB，λ/D=2、ω/D=0.36时的展向波纹结构模型已无峰值；λ/D=2、ω/D=0.36 和λ/D=4、ω/D=0.36 时的展向波纹结构模型的总声压级为129.26 dB、134.27 dB，较直方杆模型降低了8.06 dB、3.05 dB。

图18 λ/D=2、ω/D=0.36和λ/D=4、ω/D=0.36时展向波纹结构模型和直方杆模型的远场噪声频谱

图19 中直方杆模型的声压级在80°～165°的辐射角范围内均大于λ/D=2、ω/D=0.36 和λ/D=4、ω/D=0.36时的展向波纹结构模型。在75°～135°的辐射角范围内，λ/D=2、ω/D=0.36 时的展向波纹结构模型的声压级小于λ/D=4、ω/D=0.36 时的展向波纹结构模型和直方杆模型。在辐射角120°附近，λ/D=2、ω/D=0.36时的展向波纹结构模型声压级最小。

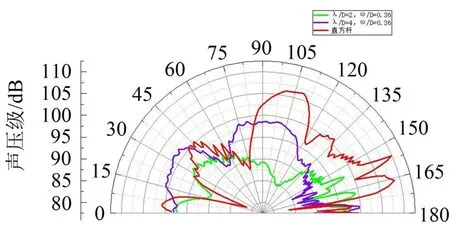
图19 λ/D=2、ω/D=0.36和λ/D=4、ω/D=0.36时展向波纹结构模型和直方杆模型的远场噪声指向性

由图20 可以看出在200 Hz～300 Hz、580 Hz～2 000 Hz 频率范围内，λ/D=2、ω/D=0.48 时的展向波纹结构模型较λ/D=4、ω/D=0.48 时的展向波纹结构模型和直方杆模型的声压级明显降低；而在0～80 Hz、420 Hz～480 Hz 频率范围内，λ/D=4、ω/D=0.48时的展向波纹结构模型的声压级较λ/D=2、ω/D=0.48时的展向波纹结构模型和直方杆模型有所降低；λ/D=2、ω/D=0.48和λ/D=4、ω/D=0.48时的展向波纹结构模型已无峰值出现；λ/D=2、ω/D=0.48和λ/D=4、ω/D=0.48 时的展向波纹结构模型总声压级为128.17 dB、130.7 dB，较直方杆模型降低了9.15 dB、6.65 dB。

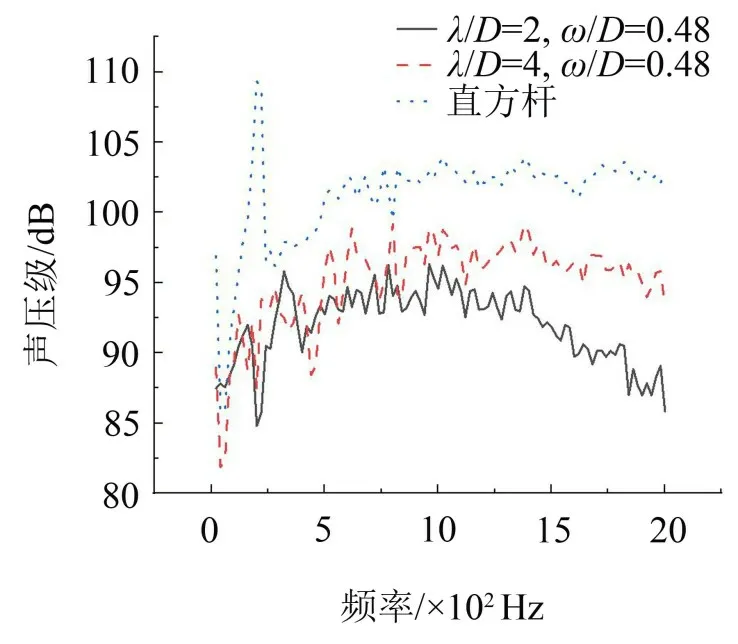
图20 λ/D=2、ω/D=0.48和λ/D=4、ω/D=0.48时展向波纹结构模型和直方杆模型的远场噪声频谱

图21 中直方杆模型的声压级在82°～170°的辐射角范围内均大于λ/D=2、ω/D=0.48和λ/D=4、ω/D=0.48 时的展向波纹结构模型。在30°～60°、70°～120°的辐射角范围内，λ/D=2、ω/D=0.48时的展向波纹结构模型的声压级小于λ/D=4、ω/D=0.48 的展向波纹结构模型和直方杆模型。在辐射角15°附近，λ/D=2、ω/D=0.48 时的展向波纹结构模型声压级最小。

图21 λ/D=2、ω/D=0.48和λ/D=4、ω/D=0.48时展向波纹结构模型和直方杆模型的远场噪声指向性

当波纹幅度ω一定时，随着波长λ的增加，展向波纹结构模型的总声压级有所增大；小波纹幅度的λ/D=2、ω/D=0.12 和λ/D=4、ω/D=0.12 时的展向波纹结构模型没有明显降低气动噪声作用，而其他参数的展向波纹结构均有明显降噪效果；当波纹幅度ω/D=0.36、ω/D=0.48时，展向波纹结构在低频段已无峰值声压级。

3.2 弓头展向波纹结构波纹幅度的影响

为进一步分析弓头展向波纹结构波纹幅度ω对气动噪声的影响，对波长λ/D=2 为定值的展向波纹结构模型和直方杆模型在R=1.18 m 测点91 处的远场噪声频谱进行分析。由图22可知在240 Hz～380 Hz频率范围内，λ/D=2、ω/D=0.36时展向波纹结构模型较其他参数的展向波纹结构模型和直方杆模型声压级有所降低；在1 081 Hz～2 000 Hz 频率范围内，λ/D=2、ω/D=0.48 时的展向波纹结构模型较其他参数的展向波纹结构模型和直方杆模型声压级显著降低。

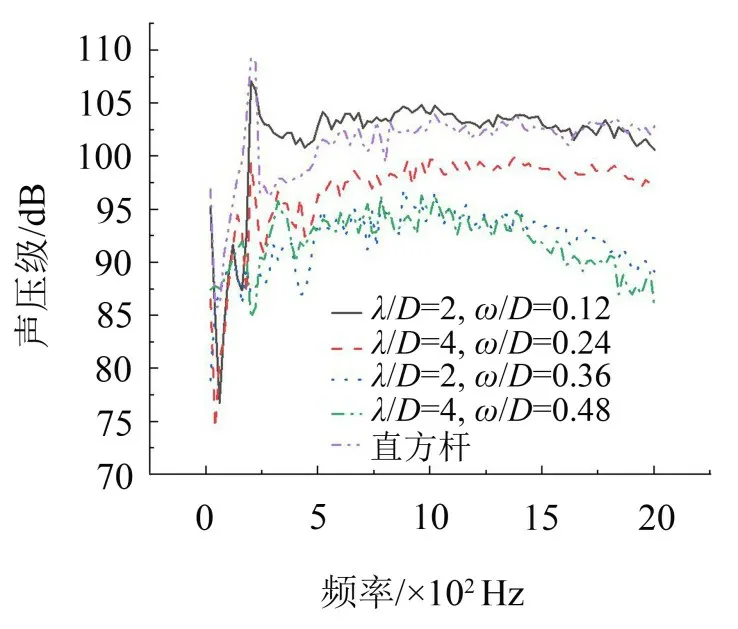
图22 λ/D=2且ω/D=0.12、λ/D=2且ω/D=0.24、λ/D=2且ω/D=0.36和λ/D=2且ω/D=0.48时展向波纹结构模型和直方杆模型的远场噪声频谱

图23为λ/D=2且ω/D=0.12、λ/D=2且ω/D=0.24、λ/D=2 且ω/D=0.36 和λ/D=2 且ω/D=0.48 时的展向波纹结构模型和直方杆模型的远场噪声指向性，直方杆模型的声压级在88°～120°的辐射角范围内均大于展向波纹结构模型。在28°～60°、75°～100°的辐射角范围内，λ/D=2、ω/D=0.48 时的展向波纹结构模型的声压级小于λ/D=2、ω/D=0.12 和λ/D=2、ω/D=0.24以及λ/D=2、ω/D=0.36 时的展向波纹结构模型和直方杆模型。在辐射角8°附近，λ/D=2、ω/D=0.48 时的展向波纹结构模型声压级最小。

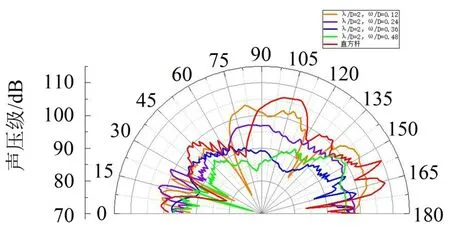
图23 λ/D=2且ω/D=0.12、λ/D=2且ω/D=0.24、λ/D=2且ω/D=0.36和λ/D=2且ω/D=0.48时展向波纹结构模型和直方杆模型的远场噪声指向性

图24为波长λ/D=4为定值的展向波纹结构模型和直方杆模型在R=1.18 m 测点91 处的远场噪声频谱。在40 Hz～1 000 Hz 频率范围内，λ/D=4、ω/D=0.36时展向波纹结构模型较其他参数的展向波纹结构模型和直方杆模型声压级有所降低；在260 Hz～2 000 Hz 频率范围内，λ/D=4、ω/D=0.48 时的展向波纹结构模型较其他参数的展向波纹结构模型和直方杆模型声压级显著降低。

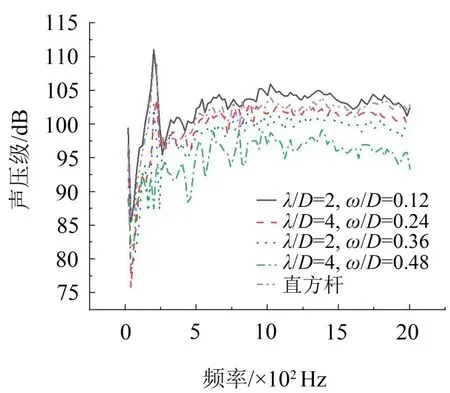
图24 λ/D=4且ω/D=0.12、λ/D=4、且ω/D=0.24、λ/D=4且ω/D=0.36和λ/D=4且ω/D=0.48时展向波纹结构模型和直方杆模型的远场噪声频谱

图25 中直方杆模型的声压级在90°～170°的辐射角范围内均大于λ/D=4且ω/D=0.12、λ/D=4且ω/D=0.24、λ/D=4 且ω/D=0.36 和λ/D=4 且ω/D=0.48 时的展向波纹结构模型。在22°～40°、80°～120°的辐射角范围内，λ/D=4、ω/D=0.48 时的展向波纹结构模型的声压级小于λ/D=2 且ω/D=0.12、λ/D=2 且ω/D=0.24、λ/D=2 且ω/D=0.36 时的展向波纹结构模型和直方杆模型。在辐射角20°附近，λ/D=4、ω/D=0.48时的展向波纹结构模型声压级最小。当波长λ一定时，随着波纹幅度ω的增加，展向波纹结构模型的总声压级逐渐降低；小波长λ/D=2 的展向波纹结构模型的降噪性能要优于λ/D=4的展向波纹结构模型；且λ/D=2、ω/D=0.48 时的降噪性能最优，其总声压级较直方杆模型降低了9.15 dB。

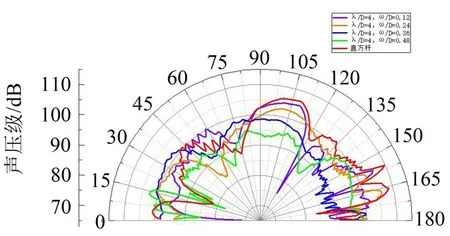
图25 λ/D=4且ω/D=0.12、λ/D=4且ω/D=0.24、λ/D=4且ω/D=0.36和λ/D=4且ω/D=0.48时展向波纹结构模型和直方杆模型的远场噪声指向性

4 仿真结果分析

表3 为8 组展向波纹结构模型和直方杆模型的气动阻力值和远场R=1.18 m处的总声压级。

从表3 中可以看出，λ/D=2、ω/D=0.36 时的展向波纹结构模型的减阻性能最优，较直方杆模型的气动阻力值降低了2.29 N；λ/D=2、ω/D=0.48时的展向波纹结构模型的降噪性能最优，较直方杆模型的总声压级在远场R=1.18 m 处降低了9.15 dB；λ/D=2 且ω/D=0.12、λ/D=4 且ω/D=0.12 时展向波纹结构模型无明显降低气动噪声作用；λ/D=2、ω/D=0.24和λ/D=4、ω/D=0.24时的展向波纹结构模型总声压级较直方杆模型降低了4.78 dB、1.66 dB；λ/D=2、ω/D=0.36 和λ/D=4、ω/D=0.36时的展向波纹结构模型总声压级较直方杆模型降低了8.06 dB、3.05 dB；λ/D=2、ω/D=0.48和λ/D=4、ω/D=0.48时的展向波纹结构模型总声压级较直方杆模型降低了9.15 dB、6.65 dB。Liu 等[10]对受电弓展向波纹结构进行了消声室内噪声风洞试验，实验结果表明展向波纹结构的峰值频率为195 Hz，高波纹幅度降噪效果明显，波长对声压级的影响较小。本文通过数值模拟得到的峰值频率为200 Hz，对于不同的波长λ/D=2、λ/D=4，展向波纹结构降噪效果不明显，而随着波纹幅度ω的增加，展向波纹结构的总声压有明显降低，这与风洞实验的结果有着良好的一致性。

表3 展向波纹结构模型的阻力值及监测点噪声值

5 结语

本研究从噪声云图、远场噪声频谱曲线、远场噪声指向性3 个方面对8 组展向波纹结构模型和直方杆模型进行优化分析，得出了以下结论：

（1）λ/D=2、ω/D=0.48时的展向波纹结构模型在远场R=1.18m处的声压级最小，降噪性能最优，较直方杆模型的总声压级降低了9.15 dB；

（2）λ/D=2、ω/D=0.36时的展向波纹结构模型的减阻性能最优，较直方杆模型的气动阻力值降低了2.29 N；

（3）当波长λ/D=2、λ/D=4 时，随着波纹度ω的增加，展向波纹结构模型的总声压级逐渐降低；

（4）当波纹度ω/D=0.12、ω/D=0.24、ω/D=0.36、ω/D=0.48时，随着波长λ的增加，展向波纹结构模型的总声压级逐渐增大；

（5）在辐射角8°附近，λ/D=2、ω/D=0.48 时的展向波纹结构模型声压级最小。

本文的研究中只选取了8组展向波纹结构模型进行仿真分析，要获得气动性能更优的结构，还需要进行多组结构参数优化以及开展多元耦合的展向波纹结构研究。