罕遇地震矮塔斜拉桥双曲面球形减震支座与液体黏滞阻尼器联合应用研究

全 伟，于鸿铭，刘旭政，王东升

(1.黄山学院建筑工程学院，安徽黄山 245041； 2.沈阳建筑大学交通工程学院，沈阳 110168； 3.华东交通大学土木建筑学院，南昌 330013；4.河北工业大学土木与交通学院，天津 300401)

近年来，随着高速铁路的不断发展，铁路桥梁跨径不断增长，矮塔斜拉桥凭借其跨径长，刚度大，成桥变形小，施工便捷和造型美观等优点，在铁路领域得到广泛应用[1-3]，成为21世纪桥梁建设中的主流桥型之一。与传统斜拉桥及连续刚构(梁)桥相比较，矮塔斜拉桥在抗震性能方面具有一定的优势[4]。由于矮塔斜拉桥的结构特性近似于多点弹性支撑的连续梁桥，使得它的适用跨径宜在100～300 m之间，若主梁采用钢与混凝土混合结构跨径有望突破400 m[5]。因此，矮塔斜拉桥成为目前大跨度铁路桥梁常用桥型之一。然而此类桥梁在地震动作用下，主要凭借主梁和主塔或桥墩间的固定支座传递水平地震力，造成固定支座吨位较大且难以满足抗震需求，特别是修建在高烈度场地上的大跨度矮塔斜拉桥，如何改善其受力状态及分布是此类桥梁抗震设计的关键问题。

桥梁抗震设计通常利用减隔震装置使桥梁结构的周期增长和增加支座处的阻尼来耗散能量，使在地震区上的桥梁结构与地震能量集中的频段隔离，从而降低结构的动力响应。李晓莉等[6]研究了高烈度震区近断层下桥梁的隔震设计，并提出采用铅芯橡胶支座和拉索限位装置的组合控制系统；陈兴冲等[7]对某矮塔斜拉桥使用黏滞阻尼器、lock-up装置及摩擦型滑动支座进行分析，得到黏滞阻尼器及lock-up装置减震效果较好；任万敏等[8]以成昆铁路攀枝花金沙江大桥(120+208+120) m预应力混凝土矮塔斜拉桥为例，使用三摩擦副双曲面摩擦摆减隔震支座+剪力榫组合支承体系，可有效减小支座顺桥向位移；游嘉玮等[9]以珠海市鸡啼门特大桥为例，得到在主墩处、交界墩处以及主梁连接处添加阻尼器可减小控制截面弯矩并限制结构位移；刘双等[10]以黑龙江大桥六塔叠合梁矮塔斜拉桥为例，对比不同消能装置联合应用的减震效果；何沁洲[11]以(89+245+185) m的独塔斜拉桥新津河大桥为研究对象，比较了固结、飘浮、弹性索体系的结构地震内力与位移响应，提出了弹性索与拉索减震支座组合设计方案；刘洋等[12]采用有限元分析软件开展液体黏滞阻尼器减震、双曲面球形隔震支座隔震研究，最终采用双曲面球形隔震支座方案；李一鸣[13]以黏滞阻尼器配合双曲面球形隔震支座进行减震设计的大跨度连续梁桥为例，通过研究竖向地震动作用下的减震效果，得到其对墩梁相对位移控制明显；贾毅[14]等以一座(67+110+360+110+67) m 大跨斜拉桥为研究对象，建立全桥动力分析模型，得到减隔震混合装置中摩擦摆支座和液体黏滞阻尼器可以协同作用，减震耗能效果明显。

在前人的研究基础上，通过联合应用双曲面球形减隔震支座和液体黏滞阻尼器，优化参数研究其对高铁矮塔斜拉桥的受力和变形结果的影响，与使用双曲面支座相比，联合应用双曲面支座和液体黏滞阻尼器能够有效控制地震作用下的墩梁相对位移，发挥二者的优势，为此类桥梁的设计提供参考。

1 工程概况(图1)

注：φ为桥桩直径。

以某高铁矮塔斜拉桥(65+85+178+93) m为例，主桥结构采用双塔双索面预应力混凝土矮塔斜拉桥，采用塔-梁固结、墩-梁分离的结构形式，梁-墩间设支座，顺桥向固定墩设在小里程侧主墩处。主梁为三向预应力结构，桥墩和桥塔采用钢筋混凝土结构，斜拉索采用扇形布置，梁上索距8 m。主塔采用双柱形桥塔，桥面以上塔高均为26 m。主塔均采用实心矩形截面，桥面以上主塔的双柱横桥向宽度均为2.0 m，顺桥向宽度为3.5 m。桥墩采用顺桥向宽5 m，横桥向宽17.3 m的圆端实体板式桥墩。

2 地震激励选取

根据地震安评报告：桥址设计基本水平地震加速度0.2g，抗震设防烈度8度，桥址场地类别Ⅱ类，设计地震分组2区，设计特征周期0.4 s。根据桥址场地条件，考虑相位随机性的影响生成3条具有随机相位的人工地震波，3条人工地震波的加速度时程曲线见图2。参考铁路工程抗震设计规范，模型中应该使用3组地震动进行时程分析，介于篇幅限制，结果取3组中的最大值。

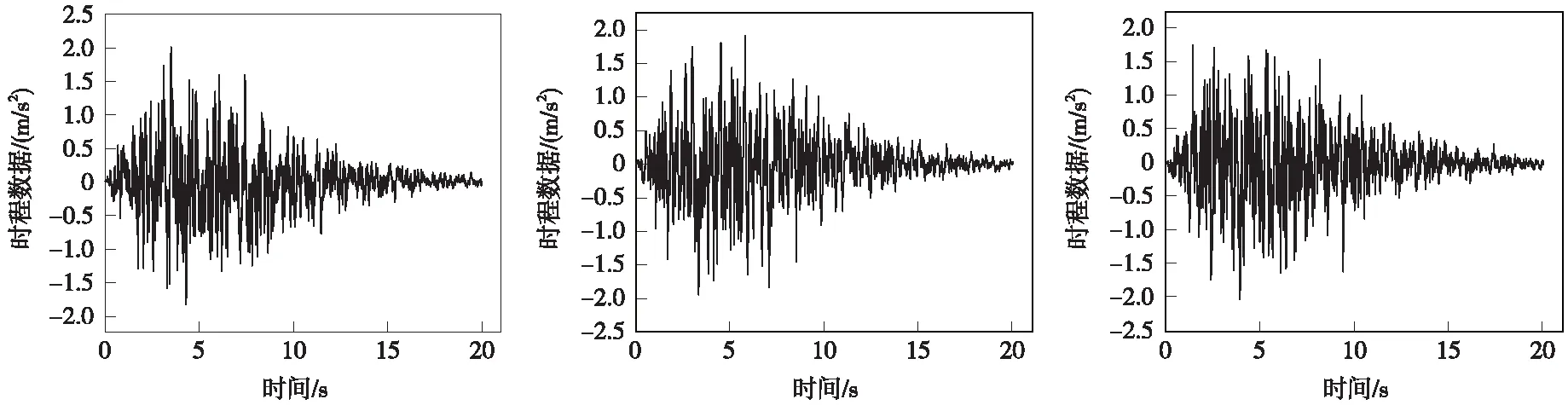
图2 3条人工地震波的加速度时程曲线

3 有限元模型

本桥采用通用有限元软件Midas Civil建模，主梁、主塔及桥墩使用梁单元进行模拟，拉索使用桁架单元进行模拟，共计385个节点，355个单元。其中，梁单元共291个、桁架单元共64个，x、y、z方向分别代表顺桥向、横桥向和竖向，全桥模型如图3所示。普通支座使用弹性连接、减震支座及阻尼器采用一般连接模拟，地基采用m法计算其等效刚度，将地基及基础对桥墩及桥塔的作用简化为弹簧施加在承台底部。地震动输入选用图2中3条人工地震动加速度时程曲线进行分析。

图3 全桥有限元模型

4 减隔震方案对比分析

本桥处于高震区，主塔固定支座处的剪力和弯矩相比其他部位要大很多，此时采用固定支座及基础满足抗震要求是不经济的，延性抗震体系震后损伤修复相对困难，因此，采用减隔震支座进行设计。减震技术一方面可提高结构的抗震性能，另一方面也可降低造价，甚至在有些情况下采用这些技术是解决实际抗震问题的唯一有效途径[15-17]。具体支座模拟情况如图4所示，图4中支座型号表示支座吨位，单位为kN；SX表示双向活动支座；ZX表示纵向活动支座；GD表示固定支座。为选取合适的减隔震支座设计参数，需对全桥进行抗震计算分析，普通支座计算结果如表1所示。

图4 普通支座布置

表1 普通支座在地震动作用下的内力位移结果

4.1 单独使用双曲面球形减隔震支座

双曲面球形减隔震支座在国内许多重大铁路工程中已有应用，如宝兰高铁、京沈高铁等[18]。双曲面球形减隔震支座是将摩擦摆支座的工作原理成功运用到常用的球型支座上的一种减隔震支座[19]，在地震不发生的情况下，其功能与普通球型支座一致，可满足桥梁的正常运行。当地震发生后，支座限位装置被剪断，限位方向约束解除发生滑动，起到减隔震作用，地震结束后，支座通过自身重力恢复原位。双曲面球形减隔震支座具有完备的减隔震功能、优异的抗震性能、良好的耐久性能，支座构造如图5所示。

图5 铁路桥梁双曲面球形减隔震支座结构(纵向活动)

双曲面支座模拟采用一般连接单元中具有二轴塑性的摩擦摆隔震装置模拟。本桥139号、140号、143号桥墩吨位较小，采用摩擦系数0.03，曲率半径为5 m的双曲面支座，在优化过程中保持支座参数不变；对141号、142号桥墩双曲面球形支座的等效曲率半径的取值为2.5～9.5 m，摩擦系数取值为0.02～0.09的支座减震效果进行了对比。建立双曲面球形减震支座模型时，使用双曲面支座代替普通支座，支座布置如图6所示。安装固定支座的主塔在添加减震装置后内力减小幅度最大，分析主塔的弯矩和墩梁相对位移计算结果如图7、图8所示。

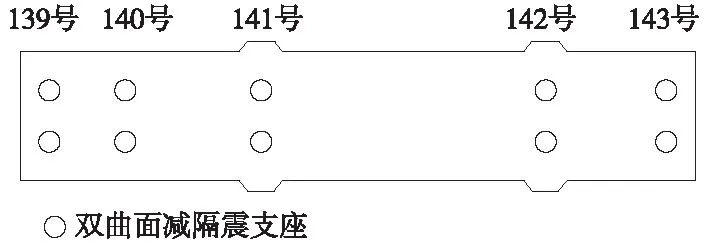
图6 双曲面支座布置示意

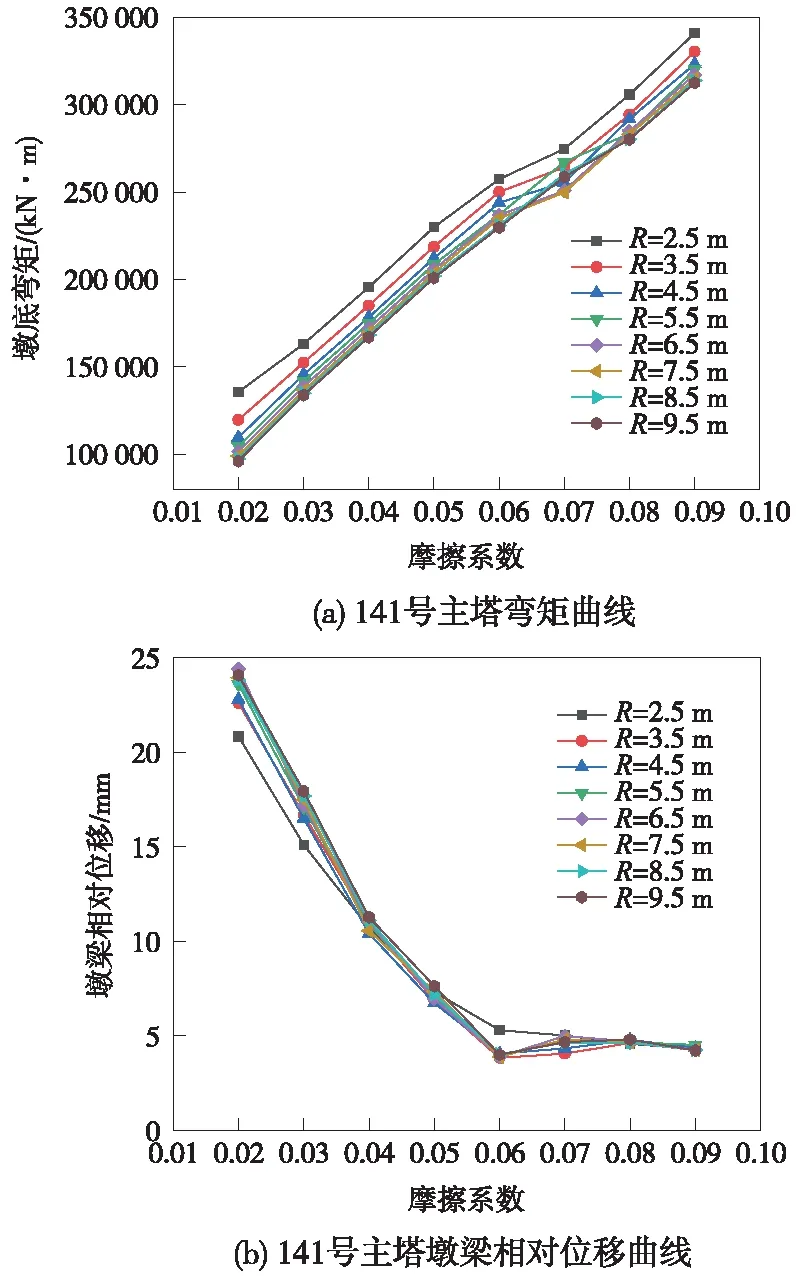
图7 141号主塔在地震动作用下内力位移结果

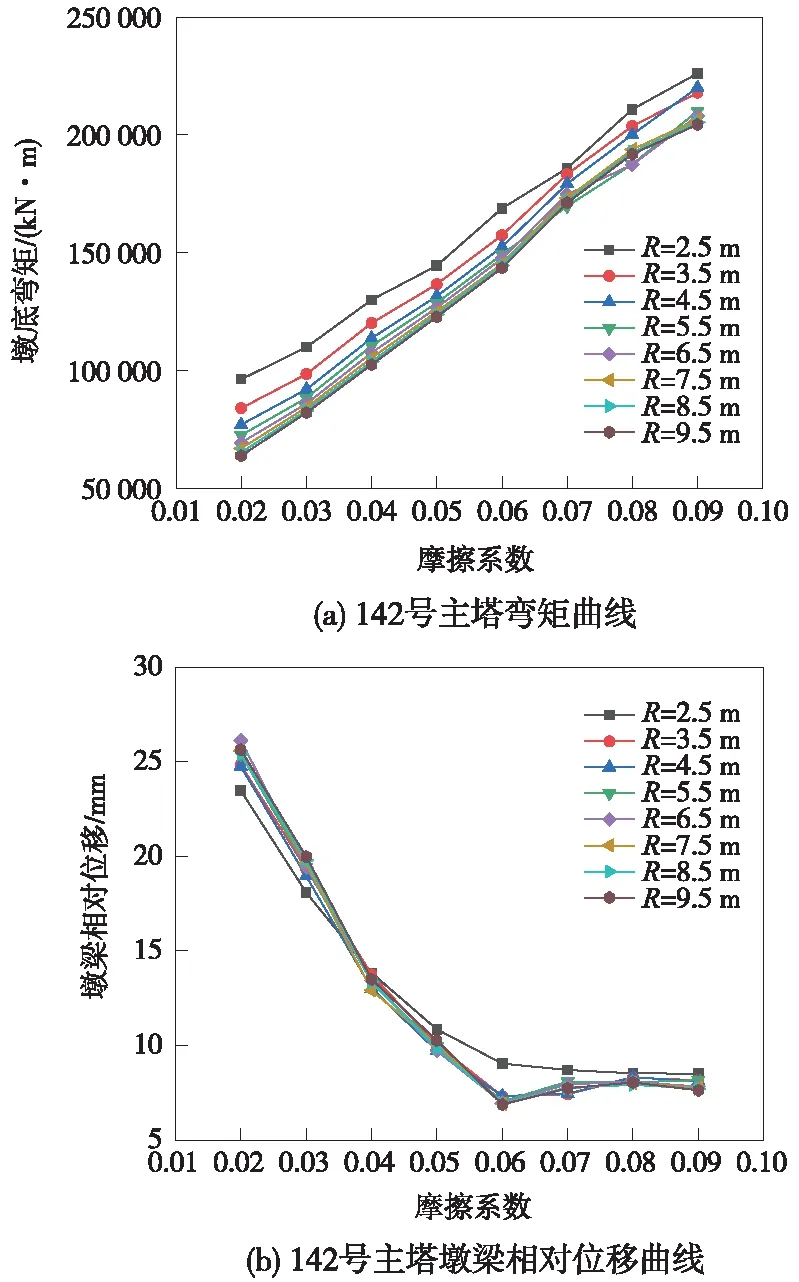
图8 142号主塔在地震动作用下内力位移计算结果

由图7、图8可知，在双曲面支座曲率半径一定的情况下，随着支座摩擦系数的增加，塔底弯矩增大，墩梁相对位移减小并在摩擦系数大于0.06时重新上升，但上升情况缓慢；在摩擦系数一定的情况下，随着曲率半径的增加，塔底弯矩减小，墩梁相对位移增大，在曲率半径大于3.5 m后受曲率半径的影响较小。综合考虑工程实际情况和材料加工等因素，结合墩底内力和位移计算结果，双曲面减震支座最优值选定摩擦系数为0.03，曲率半径为8.5 m进行后续墩梁相对位移优化，表2为模型的内力和位移计算结果。

表2 最优参数双曲面减隔震支座模型计算结果

由表2可知，未安装双曲面支座之前，141号主塔处使用固定支座，刚度较大，在罕遇地震作用下，墩底弯矩较大，由于固定支座约束，墩梁相对位移较小。安装双曲面支座后，由于双曲面支座发生滑动延长结构周期，使141号主塔支座处刚度减小，弯矩得到大幅度减小，但由于支座运动，相比固定支座，墩梁相对位移有一定程度的增加，产生位移增大现象，安装双曲面支座对141号主塔的内力有改善作用；142号桥墩处使用多向滑动支座，刚度较小，安装双曲面支座后，刚度有一定增加，因此在罕遇地震作用下墩底弯矩增加，但相比普通支座，双曲面支座使桥墩间的内力相近，有利于全桥的内力分布。

4.2 单独使用液体黏滞阻尼器

液体黏滞阻尼器采用一般连接单元中的黏弹性消能器模拟，阻尼类型选用Maxwell模型。优化模型中对黏滞系数C的取值为6 000～20 000 kN/(m/s)α，速度指数α的取值为0.3～1.0。为对比阻尼器减震效果，建立模型，通过全桥支座处安装黏滞阻尼器和仅在主塔处安装进行对比。发现全桥安装阻尼器时，在纵向罕遇地震作用下，桥塔固定支座处的剪力和弯矩相比其他部位要大很多，这是由于此时主塔处刚度较大，内力相应集中到此处造成数值较大。而仅在主塔处安装阻尼器时并没有出现此现象，因此，本桥仅在主塔桥墩处安装阻尼器，即局部减震方案[20]，并释放主塔桥墩固定支座顺桥向约束。由于142号主塔结果与141号类似，因此，仅提取141号主塔结果，支座布置及计算结果如图9、图10所示。阻尼力与速度的关系可表达为

图9 黏滞阻尼器布置

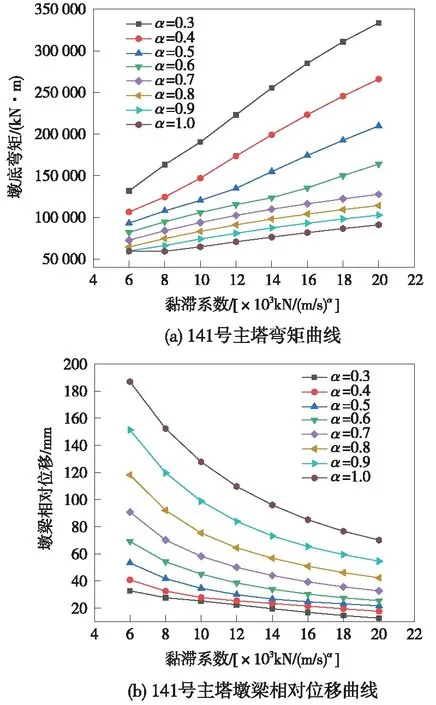
图10 141号主塔在地震动作用下的内力位移结果

F=Cvα

(1)

式中，F为阻尼力；C为黏滞系数；v为速度；α为速度指数。对阻尼器而言，速度指数越大，速度很小时就可以输出较大的阻尼力，即速度指数取值越大，阻尼器对速度的响应越敏感，但速度指数越大对制作工艺要求越高。

由图10可知，在速度指数一定的情况下，随着黏滞系数的增加，墩底弯矩增加，而墩梁相对位移减小，相比普通支座，墩梁相对位移较大；在黏滞系数一定的情况下，随着速度指数的增加，墩底弯矩减小，墩梁相对位移增大，在速度指数大于0.7后变化趋势不明显。最终选用黏滞系数为18 000 kN/(m/s)0.7，速度指数为0.7进行对比分析，表3为此模型的内力和位移计算结果。

表3 最优参数粘滞阻尼器计算结果

表3中141号主塔位移增大的原因与双曲面类似；142号主塔内力和位移增加的原因为，安装黏滞阻尼器相比固定支座释放顺桥向约束，造成刚度下降，位移增大。安装阻尼器耗能有利于全桥桥墩的内力分布，使主塔处两个桥墩的内力和位移大致相等。墩梁相对位移全桥保持在37 mm左右，相比单独使用双曲面支座时位移值27 mm有一定程度增加。

4.3 双曲面支座和黏滞阻尼器联合使用

目前，工程上常用的减隔震支座中种类较多，大多数工程中仅使用一种减隔震装置进行抗震计算分析，存在不能完全发挥减震支座结构优势的问题。通过采用双曲面球形支座和液体黏滞阻尼器联合应用的减震体系，一方面克服了主塔固定支座处弯矩和剪力响应较大的问题，另一方面解决了双曲面球支座利用支座变形来克服地震作用产生的较大变形，单独使用双曲面减隔震支座和黏滞阻尼器而造成墩梁相对位移较大的问题。模型中139号、140号、143号桥墩使用摩擦系数为0.03，曲率半径为5 m的双曲面支座，不安装黏滞阻尼器；141号、142号主塔使用摩擦系数为0.03，曲率半径为8.5 m的双曲面支座，安装黏滞阻尼器。黏滞阻尼器C黏滞系数的取值为6 000～20 000 kN/(m/s)a，a速度指数的取值为0.3～1.0进行优化，联合使用双曲面支座和黏滞阻尼器布置如图11所示，计算结果如图12所示。

图11 双曲面球形支座和黏滞阻尼器布置

由图12可知，在速度指数一定的情况下，随着黏滞系数的增加，墩梁相对位移减小；在黏滞系数一定的情况下，随着速度滞速的增加，墩梁相对位移增大，但在黏滞系数大于18 000 kN/(m/s)0.4时，速度指数为0.3和0.4的墩梁相对位移结果最小且相近。因此最终选用黏滞系数为18 000 kN/(m/s)0.4，速度指数为0.4，与双曲面支座联合应用。相比使用最优黏滞阻尼器情况下，联合使用双曲面支座和黏滞阻尼器对墩梁相对位移有很大程度的减小，墩底的内力也有一定程度减小，一方面可以进一步优化主塔的受力状况，并减小两个边墩的墩底弯矩，使内力在全桥下部结构中分配均匀；另一方面可以解决由于单独使用双曲面支座和黏滞阻尼器受到罕遇地震作用下发生滑动造成墩梁相对位移增加的情况。提取摩擦系数为0.03，曲率半径为8.5的双曲面模型、黏滞系数为18 000 kN/(m/s)0.7，速度指数为0.7的黏滞阻尼器模型和上述最优联合应用模型的墩梁相对位移结果，如表4所示。

图12 141号、142号主塔墩梁相对位移

由表4可知，在单独使用黏滞阻尼器或双曲面支座时，墩梁之间的相对位移有一定程度增加，最大增加约为99%，而联合使用上述装置对墩梁之间的相对位移有很大程度减小，最大减小幅度为69%，极大程度降低了桥梁因地震作用导致的碰撞与落梁风险。

5 结论

以某高铁矮塔斜拉桥(65+85+178+93) m为研究对象，单独使用双曲面球形减隔震支座和液体黏滞阻尼器，并将二者联合应用进行参数优化，分析桥梁的减震效果，得到以下结论。

(1)本桥使用普通支座，由于141号主塔处使用固定支座刚度较大，其余桥墩使用活动支座刚度较小，罕遇地震作用下固定支座处桥墩内力和位移相比其余桥墩要大很多，此时全桥内力和位移分布差异性较大，对抗震设计不利。

(2)采用双曲面减隔震支座后结构的整体刚度降低，纵向基本周期延长，结构的阻尼增加，固定墩内力状况得到显著改善；随着支座的曲率半径增大，墩梁相对位移增大，墩底内力减小；随着摩擦系数增加，墩梁相对位移减小，墩底内力增大。

(3)液体黏滞阻尼器不改变结构的周期、振型等动力特性。单独使用液体黏滞阻尼器，随着黏滞系数增加，阻尼器增加，墩底弯矩变大，墩梁相对位移减小；随着速度指数增加，墩底弯矩减小，墩梁相对位移增大。

(4)双曲面球形减隔震支座和液体黏滞阻尼器联合使用，相比单独应用会增加一定程度的主塔桥墩的墩底内力，相比普通支座而言全桥的内力分布状况更优，但会大大减小墩梁之间的相对位移，使双曲面球形支座和液体黏滞阻尼器充分发挥其优势，因此本桥联合使用两种减隔震装置是最合理的。

综上所述，双曲面球形减隔震支座与液体黏滞阻尼器联合应用于本桥结构的减隔震设计时，应结合矮塔斜拉桥的结构特点与减隔震设计目标，选取合适的设计参数，充分发挥二者的优势。