快速路出入口影响下的交叉口通行能力计算方法研究

齐立群

摘 要：城市道路中存在一类特殊的灯控路口，其上游或下游为快速路匝道出口或入口，该类路口受匝道附近车流交织的影响导致其通行能力不能按照常规灯控路口的通行能力进行计算。文章针对该类型灯控路口的不同分类，建立了路口通行能力的计算模型，并通过仿真的手段验证了模型具有较好的适用性。

关键词：快速路出入口;交叉口;通行能力

中图分类号：U491.23 文献标识码：A

0 引言

城市快速路是连续流交通系统，主干道是间断流交通系统。快速路出入口及其上下游的灯控路口因连接连续流与间断流交通系统，成为交通瓶颈。其原因一方面是由于快速路连续车流在遇到红绿灯后转变为间断流，导致车辆集聚引发拥堵;另一方面在快速路出入口上游或下游，常常会形成主路车流与辅路车流的交织行为，进一步降低通行能力。两方面因素的叠加导致快速路与城市干道系统衔接成为工程设计和交通组织上的难题。

1 综述

以往对于快速路出入口上下游交叉口的通行能力研究主要集中在快速路出入口的设置形式以及匝道出入口前后的交织行为的研究。

针对交织区通行能力的研究具有代表性的主要有HCM1985，HCM2000等。HCM2000通过实测的方式，给出了不同类型下交织区的取值表。后续有学者为拓展HCM中对交织区通行能力的应用范围，通过数据回归的方式，建立了交织区通行能力的理论计算模型。

90年代后，部分学者开始利用仿真的方法进行交织区通行能力的研究。但由于计算机仿真是在一定的模型基础上运行，一般可用来进行模型的检验，但对于直接得出交织区通行能力的结论尚未得到普遍的认可。

2 快速路出入口影响下的交叉口类型

根据快速路出入口的交织段与交叉口的关系，可将研究对象分为三个类型，即交织段在交叉口上游、交织段在交叉口下游和交叉口上下游具有交织段。现实条件下，第一和第二类情况较为常见，第三类情况较少见，因此文章将着重对第一和第二类情况进行研究，并建立相应的理论计算模型。

3 理论模型构建

3.1 快速路出口在交叉口上游的通行能力计算方法

3.2 快速路入口在交叉口下游的通行能力计算方法

4 模型验证

4.1 理论通行能力的计算

章节3中提出的理论通行能力计算模型涉及到交织区通行能力（CAP）和阻塞波波速的测算v，其中，交织区的通行能力参考HCM2000进行取值（为便于计算和取值，本次在仿真模型中将交织段的长度都设定为150 m）;阻塞波的波速通过仿真模型输出头部车辆通过路口的平均速度来替代。

4.2 仿真分析过程及结论

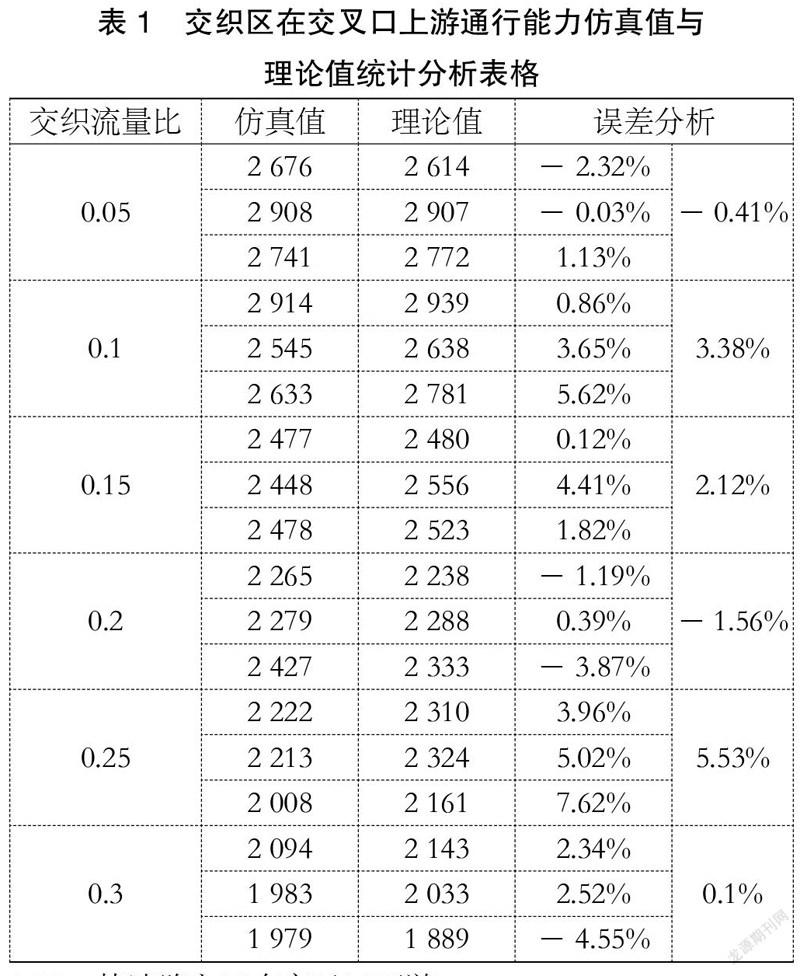
4.2.1 快速路出口在交叉口上游

为尽可能降低其他因素对模型结果的影响，在仿真系统仅建立一条长约250 m的单向道路，其中交叉口进口车道数6条，左转1条，直行4条，右转1条，匝道接地点距离路口渠化车道终点间距为150 m（即交织长度为150）。交叉口信号周期为200秒，其中绿灯时间为100秒。

仿真共进行18组，各组理论计算通行能力与仿真通行能力的差值幅度如表1所示。从表中数据可以看出仿真数据与理论数据具有较好的契合度，误差均值可控制在约5%。

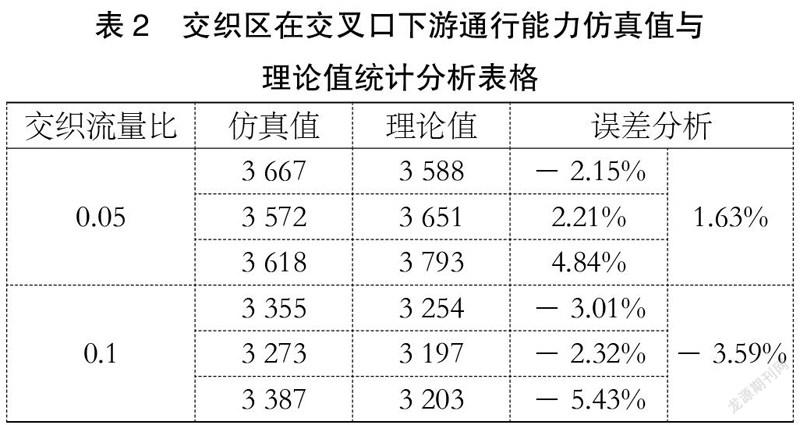
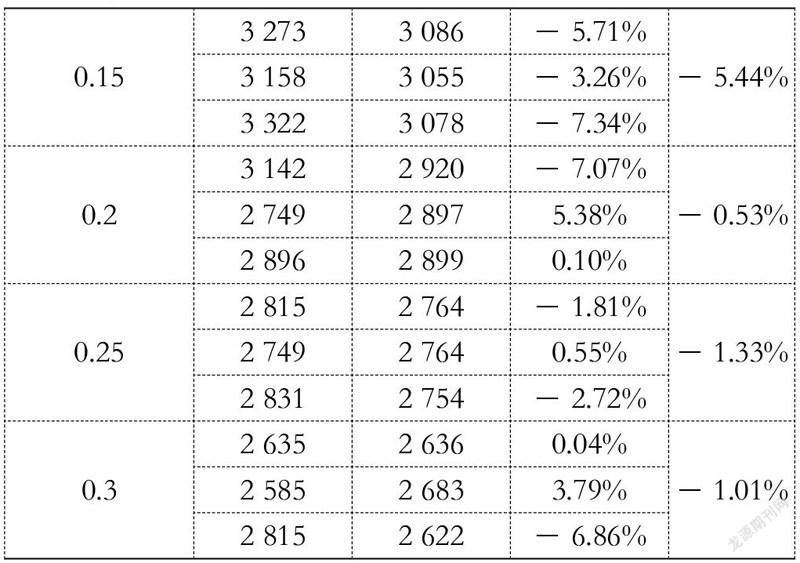
4.2.2 快速路入口在交叉口下游

類似4.2.1的方式，对交织段在交叉口下游的情况进行仿真分析。交叉口进口直行道车道数为4条，匝道接地点距离路口停止线间距为150 m（即交织长度为150）。交叉口信号周期为200秒，其中绿灯时间为100秒。

仿真进行18组，各组理论计算通行能力与仿真通行能力的差值幅度如表2所示。从表中数据可以看出仿真数据与理论数据具有较好的契合度，误差均值可控制在约5%。

5 研究结论

文章通过将快速路出入口与其上下游交叉口看作一个整体，分析快速路出入口到交叉口这一距离内车辆的运行行为，构建了快速路出入口影响下的交叉口通行能力计算模型，并通过交通仿真分析发现，模型较好的描述了快速路出入口与其附近交叉口组成的交通系统的通行能力。

参考文献：

[1]National Research Council.Highway Capacity Manual 2000[M].Washington D.C.Transportation Research Board 2000.

[2]赵靖.考虑上下游影响的信号控制交叉口通行能力研究[D].同济大学，2009.

[3]陈宽民，严宝杰.道路通行能力分析[M].人民交通出版社，2003.10.

[4]孟祥燕.高等级道路交织区通行能力研究[D].南京：东南大学交通学院，2006.

[5]罗强.上海市快速路交织区通行能力研究[D].同济大学，2007.

[6]龙科军.城市立体交叉交通规划与设计基础问题研究[D].同济大学，2005.