高中数学立体几何初步教材内容理解与教学实施

任希畅

摘  要 “立体几何初步”一直以来都是高中数学教材中的重要内容。以人教版2019年高中数学A版教材为例，分析教材的内容框架、知识编排、呈现方式等，详述如何灵活、巧妙地运用教学装备，对如何尽可能地实施直观教学提出个人见解。

关键词 高中数学;立体几何;教材;教学装备;立体几何模型

中图分类号：G633.63    文献标识码：B

文章编号：1671-489X（2021）18-0055-03

Understanding and Teaching Implementation of Textbook Pre-liminary Solid Geometry in High School Mathematics//Ren Xi-chang

Abstract “Introduction to Preliminary Solid Geometry” has always been an important teaching content in high school mathematics. This

paper takes the PEP textbook of high school mathematics in 2019 （Version A） as an example. Based on the relevant analyses of its con-

tent framework， knowledge layout， and modes of presentation， this paper elaborates on how to make good use of teaching equipment flexibly and skillfully， which provides students with intuitional instruction and puts forward references for other teachers.

Key words high school mathematics; solid geometry; textbook; tea-ching equipment; solid geometric model

0  引言

广袤宇宙和大千世界是一个实实在在的无限空间，在这个空间中存在无数大大小小、形状各不相同的物体，这些物体与人们的日常生活密切相关。自明代开始，我国先民就开始从长、宽、高三个维度，通过直观感知和度量计算等方法，认识和探索这些物体的基本属性。

据《新世纪·百科字词通典》诠释，几何学是“数学中研究点、线、面、体及其相互关系的学科”，立体几何是“研究立体图形的性质、形状、大小、位置等的学科”。现行的高中数学“立体几何初步”，就是从点、线、面、体等基础认知开始，引导学生认识空间图形的性质、形状、大小、位置等关系，从而培养发展学生的空间想象能力、推理论证能力、运用图形语言进行交流的能力、几何直观能力等，是高中阶段数学学科教学内容的重要组成部分。要使学生对教材所表达的内容和知识目标能够深刻理解、全面掌握、灵活运用，就必须从宏观和微观两个方面对教材进行详尽分析。

1  教材的编排和呈现形式

本单元教材是以长方体为载体，帮助学生认识和理解空间点、直线、平面的位置关系;用数学语言表述有关平行、垂直的性质与判定，并对某些结论进行论证;了解一些简单几何体的表面积与体积的计算方法;运用直观感知、操作确认、推理论证、度量计算等方法與过程，认识和探索空间图形的性质，建立空间观念。因此，教材的版式编排和内容呈现是非常关键的。

1.1  教材的版式呈现

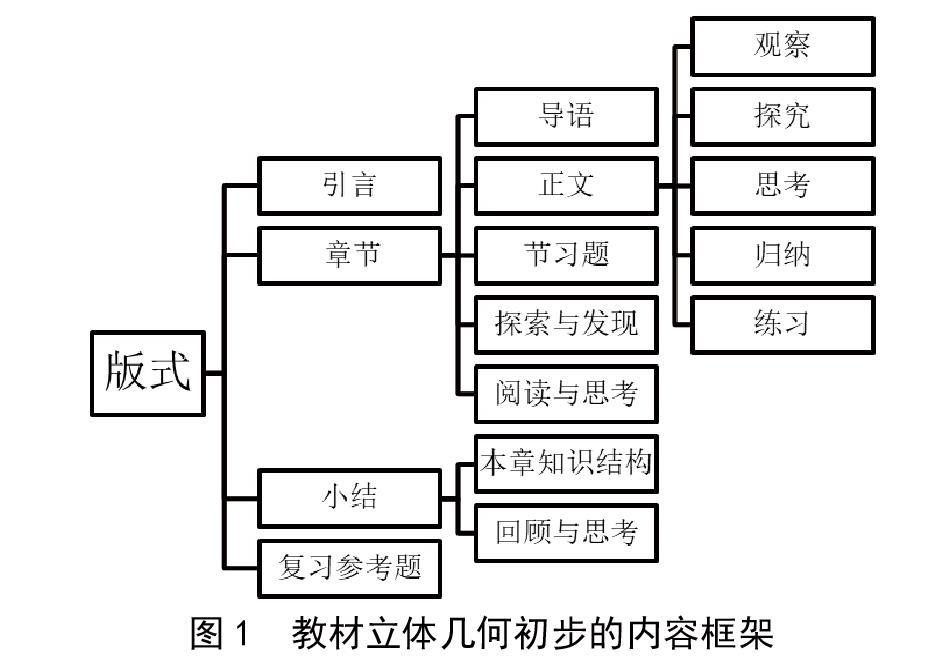
如图1所示，教材的版式依照“引言—章节—小结—复习参考题”的结构顺序展开。“章节”为正文，先讲述几何原理，接着设置相关的练习题，通过阅读思考和探索发现，帮助学生了解几何原理，然后进行“归纳”活动，统筹理解本章立体几何的基本知识。其中的“归纳”活动不但增加了学生观察和练习的形式，而且能够让学生更多地观察数学逻辑之间的联系，从而自己提出问题进行探究，逐渐形成问题式学习模式。

1.2  教材内容的编排

内容编排是教学和学习顺序的指导。教材的内容编排采用如下顺序[1]：

8.1 基本立体图形

8.2 立体图形的直观图

8.3 简单几何体的表面积与体积

8.3.1 棱柱、棱锥、棱台的表面积和体积

8.3.2 圆柱、圆锥、圆台、球的表面积和体积

8.4 空间点、直线、平面之间的位置关系

8.4.1 平面

8.4.2 空间点、直线、平面之间的位置关系

8.5 空间直线、平面的平行

8.5.1 直线与直线平行

8.5.2 直线与平面平行

8.5.3 平面与平面平行

8.6 空间直线、平面的垂直

8.6.1 直线与直线垂直

8.6.2 直线与平面垂直

8.6.3 平面与平面垂直

上述系人教版2019年高中数学A版教材的目录，从编排的顺序来看，是先整体后局部、先具体后抽象的教学与学习顺序，也即按照“立体图形—直观图—表面积与体积—点、直线、平面之间的位置关系”的编排顺序层层递进，进行学习。

从内容上看，将柱体、锥体、台体具体分为棱柱、棱锥、棱台以及圆柱、圆锥、圆台、球，这样既加强了对学生学习表面积和体积计算公式的要求，又将直线与直线、直线与平面、平面与平面三者进行组合，强调了三者之间的平行关系和垂直关系。

1.3  知识呈现方式分析

从直线与平面平行的性质定理、平面与平面垂直的判定定理这两个教学重点，来看知识呈现方式。

1.3.1  在知识导入方面  教材采用具有逻辑感的充分条件和必要条件的相互转化来导入，将判定定理和性质定理联系起来，发展学生逆向思维意识，引导学生找寻这两者之间的逻辑关系。

1.3.2  在知识体验与表征方面  教材采用给出模型并进行分析证明结论，最后得出性质定理的方式，遵循从整体到局部、从具体到抽象的原则，提供丰富的实物模型帮助学生认识空间几何体的结构特征。在表述上，教材更具有专业性和严谨性，体现数学语言的简洁精炼，引导学生逐步学会用准确的数学语言表达这些命题，直观解释命题的含义和表述证明的思路，做到直观感知、操作确认。在知识的表征上，通过语言描述的形式阐述性质定理。

1.3.3  在知识应用和知识拓展方面  以例题3为例，题中给出一种作平行线的方法，揭示了直线与平面平行中蕴藏着直线与直线平行;同时，在例题之后设置了包括填空、证明、判断三种题型的练习题进行巩固[4]。

2  教材内容的理解与学习

学习是一个系统的过程。由于高中“立体几何初步”这一章节的内容比较丰富、覆盖面比较广阔，而且知识也比较抽象，学习的难度比较大，因此必须要求师生使用归纳总结的方法，先把分散的知识进行归纳整理，使教师的教学步骤和学生的学习过程得到系统化、规律化的梳理。

2.1  从教材编排布局的情况来看

教材编排布局先呈现基本立体图形，接着呈现立体图形的直观图;然后从简单几何体包括棱柱、棱锥、棱台的表面积和体积计算逐步深入，直至圆柱、圆锥、圆台、球等的表面积和体积计算;进而引导学生认识空间点、直线、平面之间的位置关系，包括空间直线、平面的平行，空间直线、平面的垂直等。教材以螺旋上升、分层递进、逐步到位的形式，把立体几何的初步知识进行陈列。

2.2  从教材呈现的教学过程引导来看

教材先让学生通过直观观察，感知自然空间几何体的存在，然后通过计算操作来确认自然空间几何体的具体属性，最后归纳出自然空间几何体的相关空间位置关系。用这样的过程实施引导，让学生的空间思维按照教材的内容步步深入、循序渐进，直至他们完全掌握教材所表达的全部内容要求。

2.3  教材呈现的学生学习活动也是循序渐进、步步深入

教材先是对空间几何体进行反复“观察”，然后在“观察”的基础上对空间几何体的相互关系进行深入“思考”，通过“思考”对其中相关的问题进行深入“探究”，接着通过不同类型的“练习”进行训练。在“观察”“思考”“探究”“练习”等一系列活动的基础上，最后对所学的知识进行“归纳”与“总结”，同时对所用的公式进行梳理整合，从而加深对知识的理解运用。

3  立体几何模型在教学中的合理运用

充分理解教材内容是实施教学的基础，在教学实施过程中通过使用教学装备来提高教学质量是根本。普通高中学校普遍地装备了多媒体设备，同时配备了套装的立体几何模型。就装备的特点而言，多媒体器材的优势在于能够展现丰富多彩的图形，虽然这些多彩丰富的图形非常容易激发学生学习的兴趣，但是难以引导学生从平面到空间立体的思维转化。而立体几何模型虽然没有丰富多彩的图片，但是能够直接给学生一个直观立体体验，使学生的空间思维转化得到很好的锻炼。因此，笔者就立体几何模型在教学中的运用进行简单探讨。

3.1  立体几何模型实例与生活相关联

在教学本章第一节“空间几何体的结构”时，教师可以在课前布置预习作业，让学生寻找生活中空间几何体的实例，如魔方、足球等，加深现阶段学生思维中的空间几何观念，并且将数学与日常生活相联系，将数学融入生活。同时，教师可以在课堂中展示带来的一些实例模型，让学生通过观察来认识空间几何体并发现空间几何体的特点。

再者，可以通过展示名胜古迹中的立体模型来拉近空间观念与生活的距离，也可以培养学生用心观察，分析周围的数学之美。如举行一个课堂展示，请学生分享自己在假期中观察、记录下来的立体几何模型。此举意在向学生灌输学习不只是在课堂中的学习，更是平时生活中的点滴积累的理念。从实体建筑物到立体几何模型，需要经过表象到实质、整体到局部，认真比对、反复研究，按照比例尺缩小尺寸，将偌大復杂的建筑物分解成若干个小的简单几何体，培养学生数学抽象的能力。

如果有条件提供多媒体教室的教学环境，教师可以组织学生小组合作，探索通过“画图”软件进行立体几何模型的绘制与设计，并在画图的过程中体会模型的建立过程，培养学生的数学模型核心素养，为之后“立体几何初步”的学习奠定基础。另外，初次利用软件必然会遇到挑战，因此有必要开展小组合作，通过一起出谋划策与合作协商，最后由小组成员一起对所设计的作品进行展示和解说，提高学生的数学表达能力，创造一堂精彩的拓展课程。

3.2  利用立体几何教具模型深化空间观念

在本章教学中，教师可以通过展示立体几何教具模型来为学生讲授空间几何体的三视图和直观图，培养学生的直观想象能力，并且教具可以更加清楚明白地展示各个面的特点，实现几何研究从“点—线—面—体”的研究思路，有利于构建学生思维中的空间几何体的模型架构，便于在做题或者之后立体几何计算的学习中理解图形，有效地画出图形并得出结论。

另外，为了培养学生的实践动手能力，在教学过程中创设以小组为单位制作立体几何模型的活动也不失为一种新课改背景下的教学创新。此活动不仅可以提升学生合作活动时的配合默契度，更能让学生在制作过程中发现立体几何图形的特点，并更好地掌握空间几何体的结构、空间几何体的三视图和直观图以及观察发现点、直线、平面之间的位置关系，同时在平时练习时可以加深记忆[5]。

4  结束语

立体几何的学习看似平常，但要能够全面掌握其中的原理，熟练运用相关的方法与技术，对自然空间几何体的性质进行准确判定，一般地说，教师就必须引导学生按照教材编定的程序，先从对空间几何体的整体观察入手，再直观认识和理解空间点、线、面的位置关系，最后对相关几何体进行性质判定。■

参考文献

[1]中学数学课程教材研究开发中心.普通高中教科书数学必修：第二册（A版）[M].北京：人民教育出版社，2019：

96-171.

[2]中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2020.

[3]叶立军，王思凯.两版高中数学教材“三角函数”内容比较研究：以人教2019年A版和2004年A版教材为例[J].中学数学杂志，2020（7）：1-6.

[4]叶立军，戚方柔.中美初中“圆”内容比较研究：以浙教版、人教版、美国GMH教材为例[J].中学数学月刊，

2020（4）：44-48.

[5]林妙勇.引入立体模型提升立体几何教学效果[J].广西教育，2019（6）：108-109.