精密减速器检测仪测角误差补偿
裘祖荣,周 磊,薛 洁,于 振
(天津大学精密测试技术及仪器国家重点实验室,天津300072)
1 引 言
精密减速器具有传动精度高、结构紧凑、可靠性高等优点,已成为工业机器人的核心部件,并广泛应用于先进制造、航空航天等领域。为了提高减速器的质量水平,必须对精密减速器的传动效率、传动误差、扭转刚度和空程等参数进行检测。减速器各项性能指标参数显示,角位移是减速器性能测试中不可或缺的基本量之一。当前,国内减速器检测仪大多选择高精度、高分辨力、高响应速度的圆光栅来测量角度。但是,由于安装偏心、光栅变形以及环境干扰等因素对圆光栅角度测量的影响,其测角精度往往不能达到其标称数值,严重地影响了高精度减速器检测仪的测角精度[1-2]。因此,需要研究实际工况下圆光栅的测角误差及其补偿方法,进而实现圆光栅的测角精度,保障检测仪的高精度要求。
目前,国内外减速器检测仪测角精度提高的措施主要分两种:(1)采用多读数头自校准的方法抑制对应阶次的测角误差,该方法可以从原理上抑制测角误差,但需要布置多个读数头,硬件成本较高[3-4];(2)采用多项式法、三次样条插值法、误差谐波法等数值补偿算法对圆光栅测角误差进行拟合。其中,误差谐波法应用最为广泛,其拟合的测角误差具有周期性,遵循圆周误差封闭原则,尤其适合圆光栅测角误差的补偿[5-8]。但上述算法的采样点个数被多面棱体工作面的个数限制,需要利用圆光栅N个角位置处的测角误差数据拟合出整周期测角误差模型,参与拟合的样本点过少,拟合出的测角误差模型不能充分反映圆光栅整周期测角误差,补偿效果有限。
本文利用光电自准直仪结合正24 面棱体,对精密减速器检测仪圆光栅测角系统的测角误差进行了标定和补偿。在标定过程中,将多面棱体与测量轴系固接,实现多面棱体与圆光栅同步转动。通过控制系统驱动电机旋转固定角度(15°),使得多面棱体与圆光栅稳定在指定位置,此时数据采集系统同步采集两者的角度信号。在标定实验结束后,自动生成报表并将其带入测角误差拟合程序中。利用误差谐波法对多组测量数据进行预处理,将多组测量数据相关联,再利用神经网络无需计算出具体补偿式的特点,将预处理后的测量数据作为训练点,拟合出圆光栅测角误差模型。该方法将多个圆光栅角位置处的测角误差结合起来,增加了采样点数,实现了多面棱体工作面的拓展,在误差谐波法的基础上进一步提高了圆光栅测角系统的精度,从而使减速器检测仪的测角精度达到亚角秒级。
2 圆光栅测角误差模型
2.1 精密减速器检测仪测角系统
如图1 所示,精密减速器检测仪测角系统的核心组件包括圆光栅和两个对径安装的读数头,在高速端和低速端处各有一套角度测量系统,串联在整个测量轴系中。减速器检测仪测角精度主要受到圆光栅测角精度的限制,若想提高检测仪的测角精度,需要建立圆光栅的测角误差模型并对其进行补偿。其中,影响圆光栅测角精度的主要误差源包括:圆光栅自身刻线误差、读数头电子细分误差、安装误差、轴系晃动误差以及光栅变形引入的误差[9-10]。
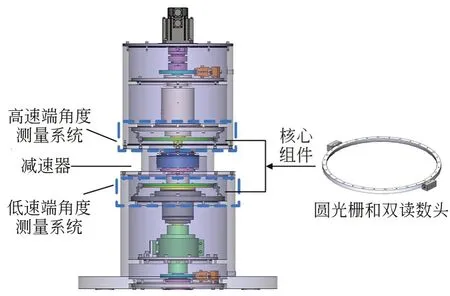
图1 精密减速器检测仪测角系统Fig.1 Angle measuring system of precision reducer tester
2.2 误差谐波算法
误差谐波算法来源于函数的傅里叶级数展开,其拟合的误差具有周期性,尤其适用于对具有圆封闭特性的圆光栅测角信号进行补偿。若想进一步提高补偿精度,需要增加采样点个数。但采样点过多时,误差谐波法所得模型复杂,容易出现拟合震荡的情况。其原理是利用圆光栅角度误差信号的周期性,将不同时间段内测得的角度信号进行三角形式的傅里叶级数分解,选取其中幅值、相位基本不变的阶次拟合出测角误差模型,建立谐波测角误差模型[11]。
2.3 BP 神经网络算法
BP 神经网络算法具有很强的非线性映射能力和泛化能力,其模型包含一个输入层、至少一个隐含层以及一个输出层。该算法无需考虑补偿对象的线性或非线性,只关注输入和输出情况。在系统稳定、环境因素影响较小的情况下效果更好,尤其适用于样本点较多的情况,补偿精度高[12]。
在圆光栅测角误差补偿系统中,输入为圆光栅角位置,输出为对应的测角误差,因此选用单输入-单输出的BP 神经网络模型。其三层结构为1×N×1,输入层和输出层的神经元个数均取1,隐含层神经元个数N通过经验公式和训练点数试算后确定,即:
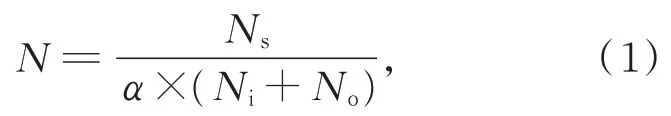
其中:Ni是输入神经元个数,No是输出神经元个数,Ns是训练点个数,α为自取的任意值变量,通常范围可取1~10。
2.4 谐波-神经网络组合补偿算法
通常情况下,采用多项式补偿法、误差谐波法等传统数值补偿法对圆光栅测角误差进行拟合时,采样点个数被多面棱体工作面个数N限制,拟合出的圆光栅测角误差模型不能充分反映圆光栅测角误差特征,补偿效果有限。鉴于此,本文将误差谐波法和BP 神经网络法相结合,通过多次标定过程增加了采样点数,在误差谐波法的基础上进一步提高了圆光栅的测角精度,满足了减速器检测仪测角系统的高精度要求。谐波-神经网络组合补偿法的具体实施步骤如下:
步骤1:测量多组不同起始角的位置误差数据。将24 面棱体安装在装有待测光栅的轴系上,多面棱体第 1 个工作面对准圆光栅 0°(±1°),进行单次测角误差标定实验,重复测量5 次,得到第1 组测角误差数据。随后小角度旋转多面棱体,将第一个工作面分别对准圆光栅 5°,10°(±1°),再次进行测角误差标定实验,得到第2 组和第3组测角误差数据k=1,2,…,24。
步骤2:拟合误差曲线。采用误差谐波法,使用第1 组测角误差标定实验所得的24 个圆光栅角位置的相对误差数据,拟合出圆光栅测角误差模型f(θ)。
步骤3:多组误差数据预处理。选取测角误差模型f(θ)上一段升降趋势稳定或者误差波动较小的角位置区间以该区间的角位置及其对应测角误差为绝对误差基准。选取其他两组数据中落在该区间的角位置用该角位置所对应的测角误差拟合值减去实际相对误差分别得到第 2 组和第 3 组的调节系数即有:
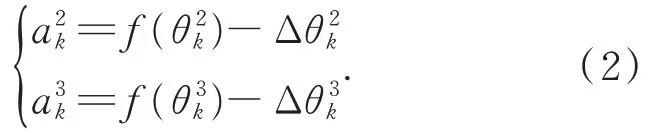
随后将第2 组和第3 组数据中所有角位置对应的相对测角误差 Δθ分别加上得到预处理后测角误差Δθ′,将各组测量数据关联。
其中:
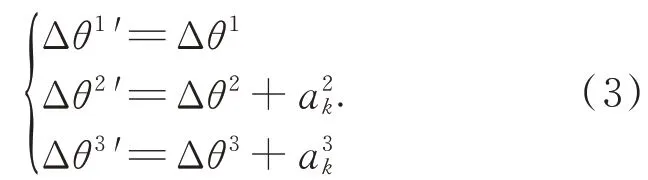
步骤4:将预处理后的角位置-误差数据(θ,Δθ′)代入神经网络中,依据式(3)得到隐含层神经元个数的取值范围,并根据拟合所得的补偿模型补偿效果和拟合用时,选取BP 神经网络的隐含层神经元个数、学习率和训练方法等参数,并得到最终的圆光栅测角误差模型。
3 自动标定系统设计
3.1 多面棱体结合自准直仪测试方法
以自准直仪对准多面棱体1 号工作面为起始点,同步采集自准直仪和圆光栅读数头的数据,随后以24 面棱体标准角度15°旋转测量轴系并记录数据,重复旋转轴系并记录数据,直至完成棱体所有工作面的数据采集。
记多面棱体第i个工作面的角位置值为αi,对应圆光栅的角位置值为βi。得到多面棱体各工作面角位置后,以多面棱体转过的角位移(αi-α1)为参考值,圆光栅转过的角位移(βi-β1)为测量值,得到对应圆光栅角位置的误差:
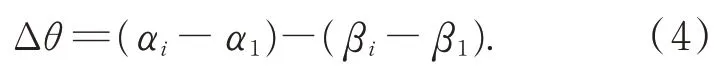
其中,多面棱体的角位置αi由三个部分组成,分别是多面棱体第i个工作面角度、光电自准直仪测量值ε及多面棱体经计量院检定后的工作面偏差λ,即:
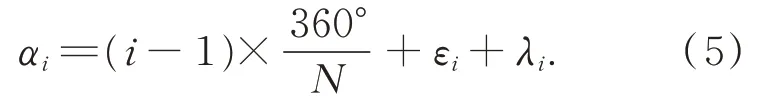
3.2 圆光栅测角误差自动标定系统组成
自动标定系统的硬件系统架构如图2 所示,包含上位机模块、下位机模块、驱动模块、圆光栅模块和自准直仪模块。此架构功能强大,开发周期短,易于维护升级。
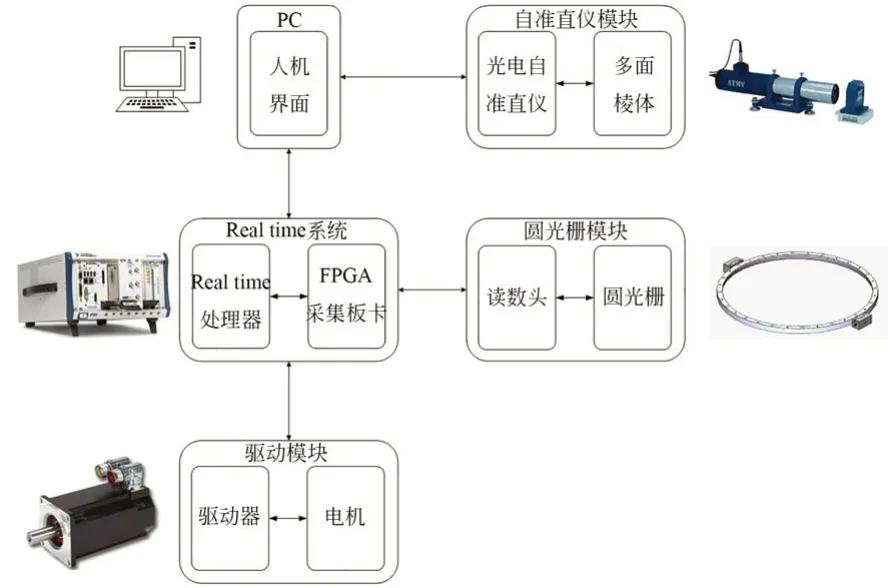
图2 嵌入式控制与信号采集系统架构示意图Fig.2 Schematic diagram of embedded control and signal acquisition system
上位机模块负责人机交互,并对自准直仪读数进行采集;下位机模块由RT 处理器和FPGA 采集板卡共同构成,将上位机命令传递至电机驱动器从而控制电机旋转,采集存储圆光栅读数头的测角信号;自准直仪模块包括24面棱体和双轴光电自准直仪,其中24 面棱体精度等级为0 级,检定精度为0.1″,光电自准直仪的测量值在±100″范围内的精度为±0.5″,重复性为0.3″,分辨力为0.1″;圆光栅模块包括圆光栅和两个对径安装的读数头,待补偿的圆光栅为雷尼绍绝对式圆光栅RESA-30U-SA3000,其标称测角精度为±0.95″,对径安装的读数头可减小光栅安装偏心所引入的测角误差。
最终搭建的实验装置实物如图3 所示,其中TESA 测头用于辅助调节多面棱体的端面跳动,转接件将多面棱体与测量轴系固接。

图3 测角误差标定实验装置Fig.3 Experimental setup for calibration of angle mea⁃surement error
3.3 圆光栅测角误差自动标定系统控制软件
为提高实验效率,编写了自动标定采集软件,实现“一键式”自动标定,流程如图4 所示。其中,自准直仪X轴方向与多面棱体旋转方向重合,其读数的变化值代表多面棱体旋转角度。
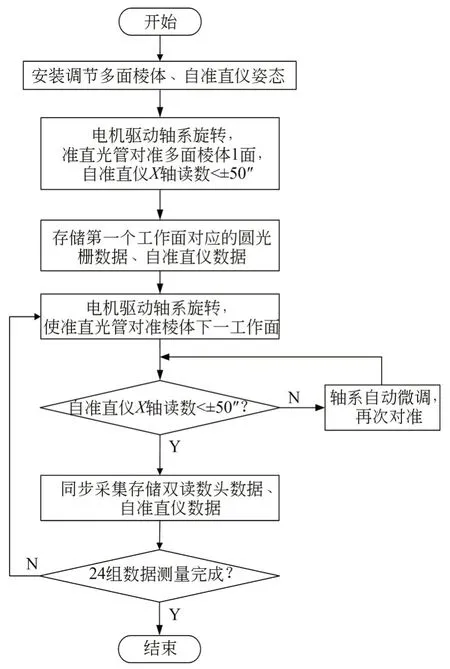
图4 自动标定流程Fig.4 Flow chart of automatic calibration
上位机程序前面板如图5 所示,包含命令模块、自准直仪模块和RT 控制模块,命令模块有开始、停止和选择高速端/低速端的功能;自准直仪模块可以对自准直仪参数进行设置,显示自准直仪的工作状态和计数次数,采集存储自准直仪读数;RT 控制模块可以驱动电机旋转固定角度并稳定在指定位置,显示圆光栅读数头计数次数,采集存储圆光栅读数头信号。
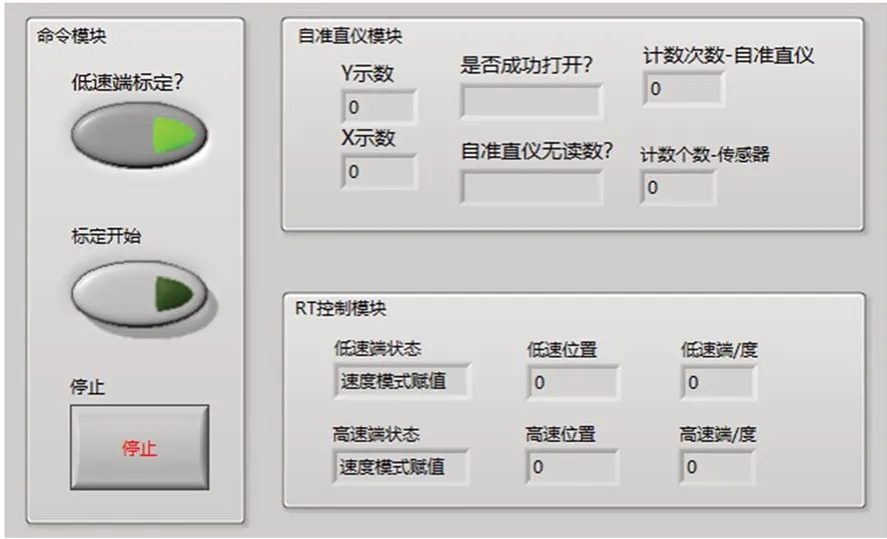
图5 自动标定系统操作界面Fig.5 Operation interface of automatic calibration system
4 实 验
4.1 圆光栅测角误差补偿实验结果
将多面棱体第一个工作面与圆光栅零点对齐,在不同时间段内重复进行5 次测角误差标定实验,所得离散角度误差数据如图6 所示,未补偿时角度误差数据集中在(-4.02″,2.12″)之间。
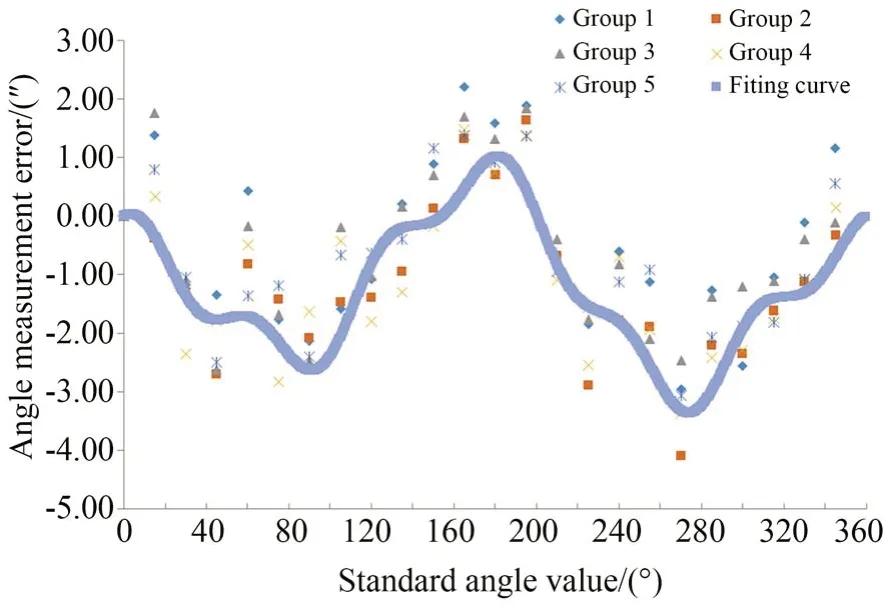
图6 测角误差数据及误差谐波法拟合曲线Fig.6 Angle measurement error data and harmonic com⁃pensation curve
采用误差谐波法分别求解出单次实验误差谐波的各阶次幅值相位,如表1 所示。可以发现,1,2,6 阶谐波幅值相位变化较小,为系统误差的主要阶次,因此测角误差模型的表达式为:
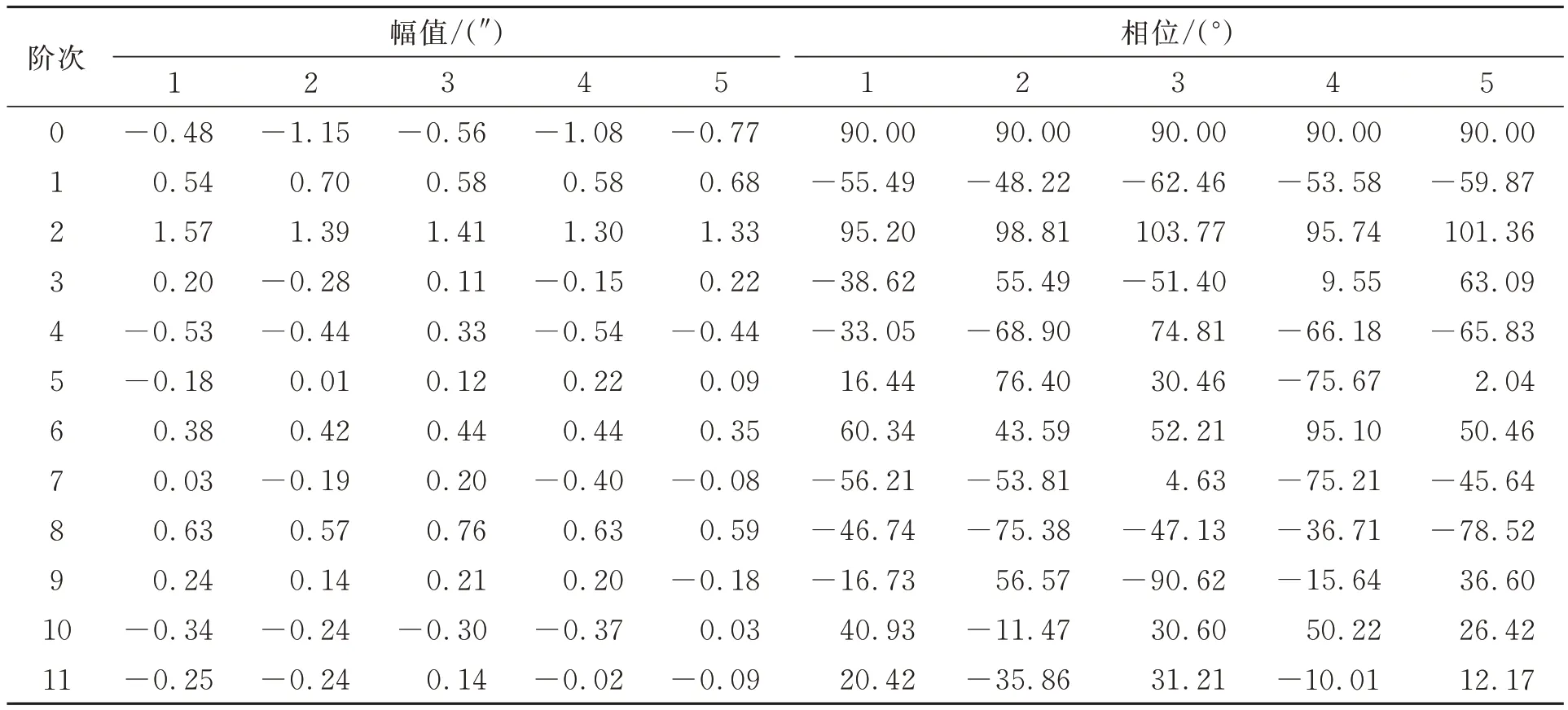
表1 误差谐波法所得的幅值相位Tab.1 Amplitude and phase obtained by error harmonic method
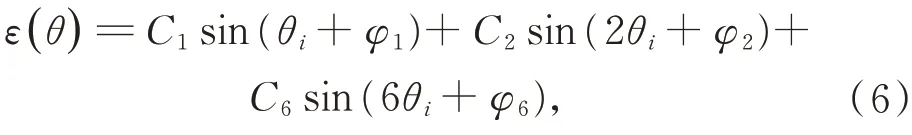
其中:θ为圆光栅角位置;φ为测角误差值。
将选取的各阶次相位幅值取5 次实验平均值,得到:
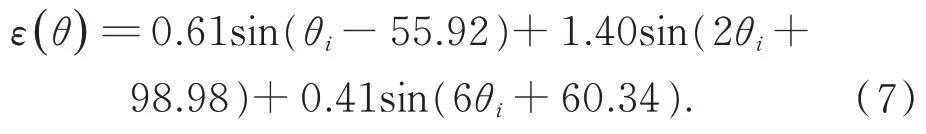
选取(0°,15°)为基准区间,对其他两组数据进行预处理,将所得角位置点θ和对应测角误差Δθ′作为训练点代入BP 神经网络中,得到圆光栅全周期测角误差模型。经反复实验后,选取神经网络模型参数如下:隐含层神经节点个数设置为36,训练目标设置为0.01,学习率设置为0.05。在该参数下系统稳定收敛,且收敛速度较快。训练点与谐波-神经网络组合补偿法所得的测角误差模型如图7 所示。
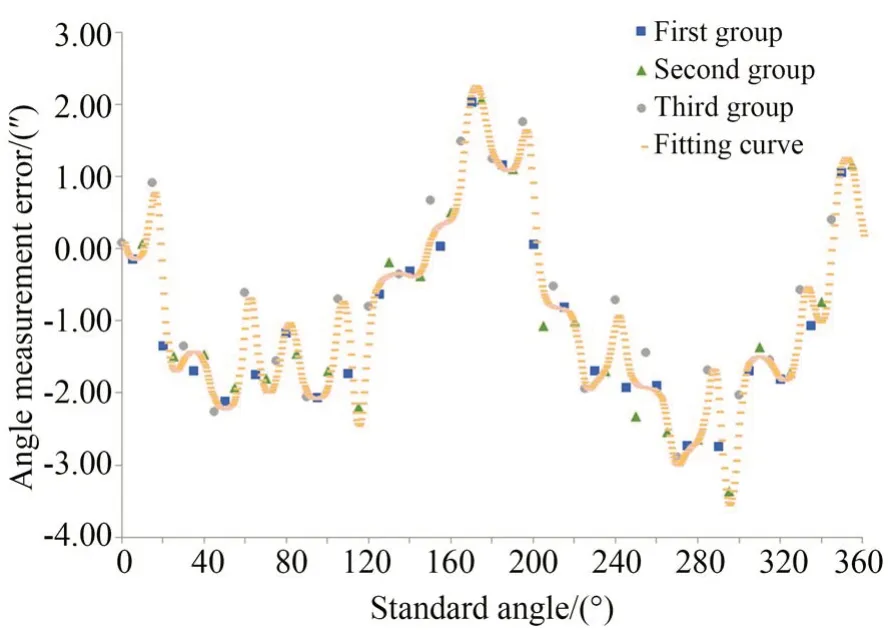
图7 训练点与谐波-神经网络组合补偿法所得的测角误差模型Fig.7 Angle measurement error model obtained by train⁃ing point and harmonic neural network combined compensation method
4.2 误差模型有效性实验验证
为了验证谐波-神经网络组合补偿法的补偿效果,随机改变多面棱体和圆光栅在周向方向的相对位置进行拓展实验,本文随机选取了多面棱体第1 个工作面与圆光栅8.17°对齐的位置。再次进行测角误差标定实验,得到24 个圆光栅角位置处的相对测角误差,分别使用误差谐波法和谐波-神经网络组合补偿法拟合出的测角误差模型对所得数据进行补偿。
补偿前后的验证数据如表2 所示,可以看出,补偿前测角误差集中在(-3.47″,1.89″),误差谐波法补偿后测角误差集中在(-1.29″,1.52″),谐波-神经网络组合补偿法补偿后的测角误差集中在(-0.84″,0.10″)。
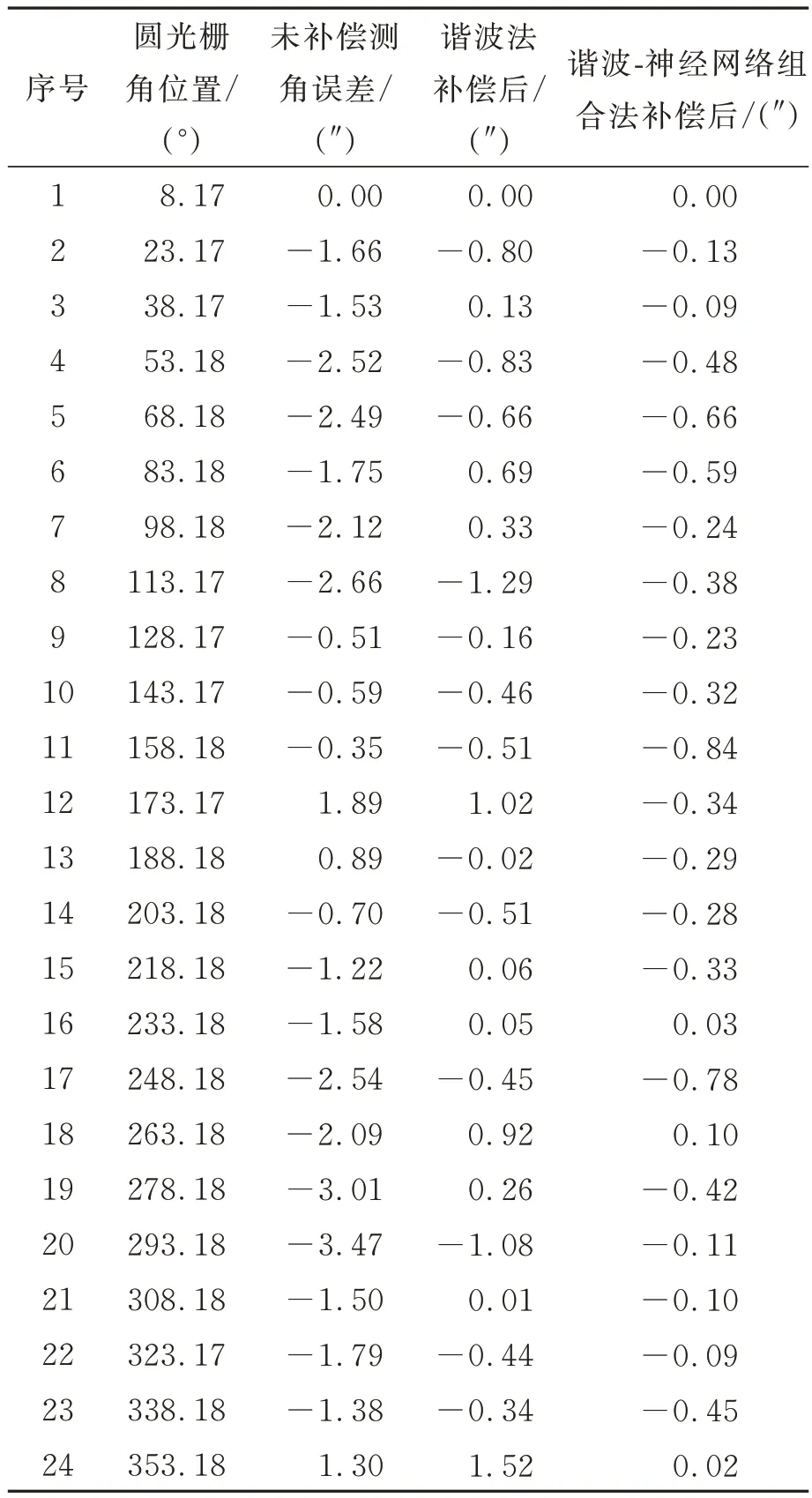
表2 验证点补偿前后的测角误差Tab.2 Angle measurement error before and after com⁃pensation of verification points
对比曲线如图8 所示,补偿前测角误差峰峰值为5.36″,标准差为1.32″;采用误差谐波法修正后测角误差峰峰值为2.82″,标准差为0.66″;谐波-神经网络组合补偿法修正后测角误差峰峰值为0.94″,标准差为0.25″,分别减小至误差谐波法补偿后的33.3%和37.9%。由此可见,采用谐波-神经网络组合补偿法拟合的测角误差补偿模型,可以进一步提高减速器检测仪的测角精度。
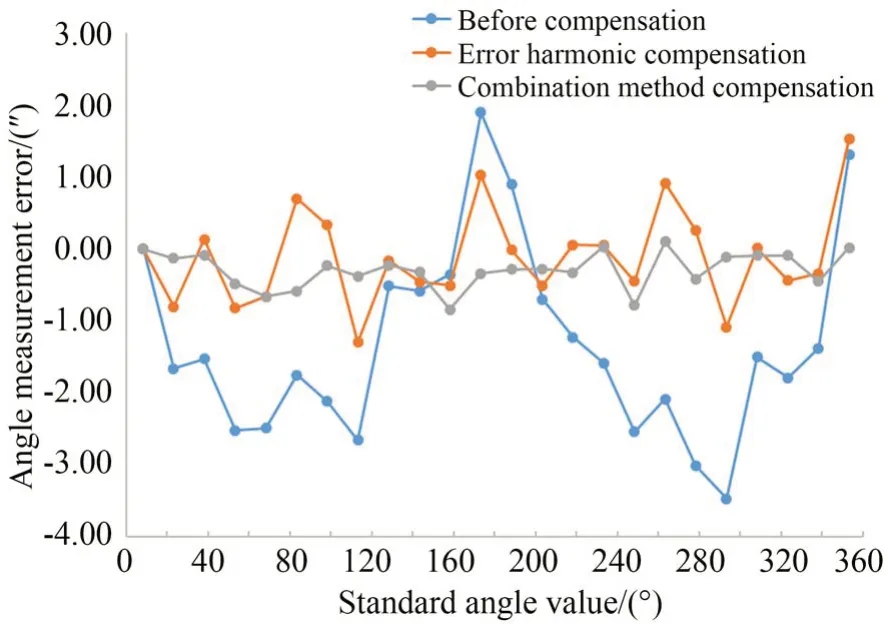
图8 误差谐波法与谐波-神经网络组合补偿法的残差对比Fig.8 Comparison of residuals between error harmonic method and harmonic neural network combined compensation method
5 不确定度分析
经补偿后的角度测量系统误差须达到亚角秒级别,此外,谐波-神经网络组合补偿法需要结合多个角位置的误差数据,在测试过程中需要小范围调节多面棱体和圆光栅周向方向上的相对位置,也会引入不确定度,因此需要对自动标定系统进行不确定度分析。标准不确定度u是各标准不确定度分量ui的合成。ui可由被测量可能值区间的半宽度U除以包含因子k表示[13]。
5.1 光电自准直仪引入的不确定度
5.1.1 示值误差
由检定证书可得,自准直仪在±100″内读数精度为 0.5″,当U=0.5″,k=2,则0.25″。
5.1.2 自准直仪的十字线倾斜引起的读数误差
理想情况如图9(a)所示,自准直仪竖直方向十字线与旋转轴线重合,多面棱体绕旋转轴OY旋转的真实角度即为自准直仪X轴的示数变化值x,Y轴的示数保持不变。实际工况如图9(b)所示,多面棱体绕OY轴旋转时,自准直仪X轴的示数变化与实际偏转角度不等,测量误差为:
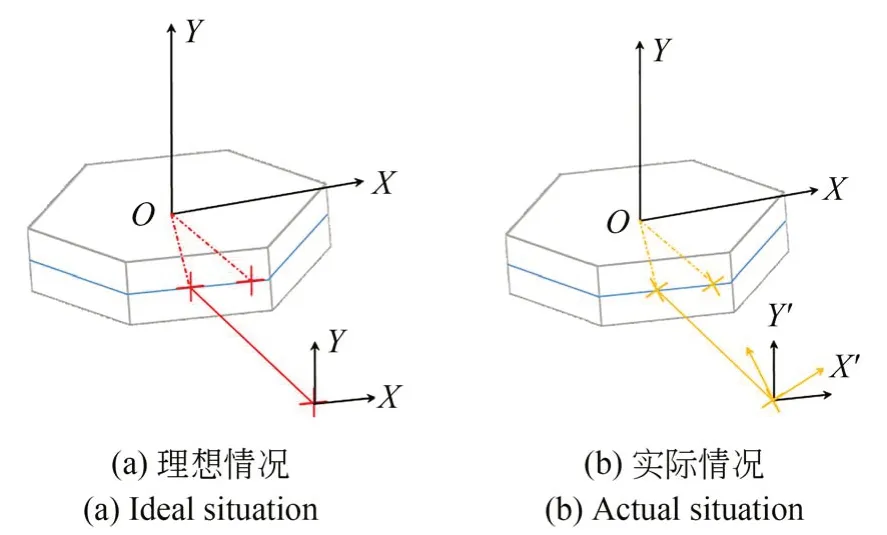
图9 自准直仪十字线倾斜示意图Fig.9 Schematic diagram of autocollimator cross line tilt
其中:x′为X轴读数,y′为Y轴读数,θ为十字线倾斜角度[14]。
本实验中,调节自准直仪姿态,直至满足多面棱体绕OY轴转动±1 500″时,Y轴的示数变化在3″内,即倾斜角度θ≤0.055°。在此条件下,若自准直仪的X,Y轴读数在±50″内时,测量误差最大值ξ1max=0.097″,误差规律近似矩形分布,
5.1.3 数显漂移引起的读数误差
单组标定实验测试用时约为15 min,将自准直仪对准多面棱体工作面,测试其30 min 内的漂移情况,采样频率为0.5 Hz。实验结果如图11所示。读数算数平均值为9.23″,峰峰值为0.23″,实验标准偏差为u3=0.03″。
5.2 多面棱体引入的不确定度
5.2.1 检定误差
本实验所用多面棱体精度等级为0 级,由检定证书得,U=0.1″,k=2,则
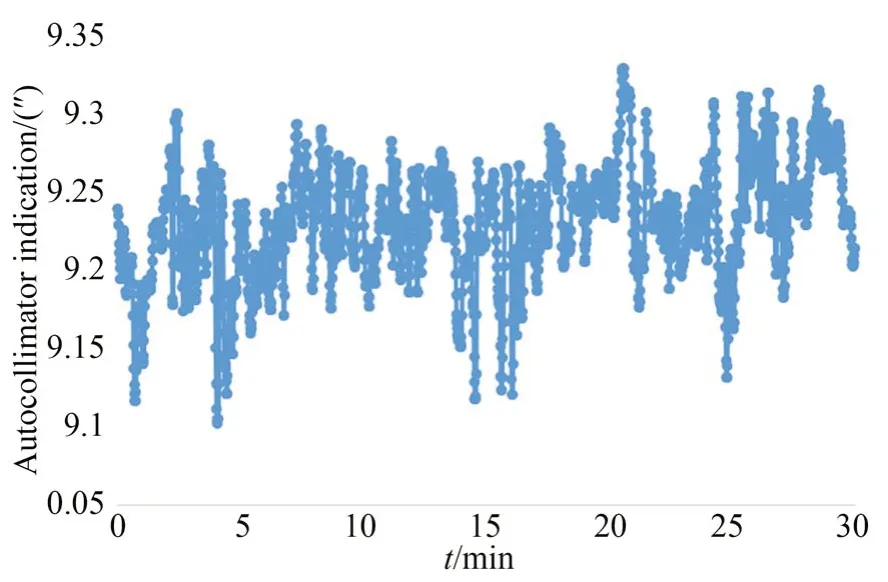
图10 自准直仪X 轴示数漂移Fig.10 Data drift of autocollimator in X-axis
5.2.2 多面棱体安装偏心引入的不确定度
多面棱体的安装偏心影响自准直仪十字光线在多面棱体工作面上的位置,进而引入多面棱体工作面的平面度误差,由此引入的测角误差为:
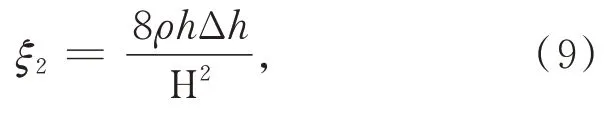
其中:ρ为弧度与角秒间的转换常数,ρ=206 265;h为棱体工作面的平面度误差;Δh为自准直仪光线改变位置的距离;H为棱体工作面的宽度[15]。
本实验所使用的多面棱体单个工作面宽度H=30 mm,平面度误差h小于 50 nm,当 Δh=0.5 mm 时,引入的测角误差最大值ξ2max=0.046″。
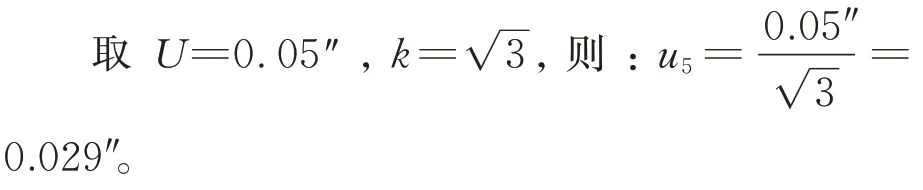
5.2.3 多面棱体安装倾斜引入的不确定度
由多面棱体安装倾斜所造成的测角误差可近似为:

其中:α为多面棱体轴线倾斜角,γi为多面棱体的旋转角度。
实验中调节多面棱体姿态,使得α<100″,0°<γi<360°,则由多面棱体安装倾斜引入的误差最大值为ξ3max=0.098″。
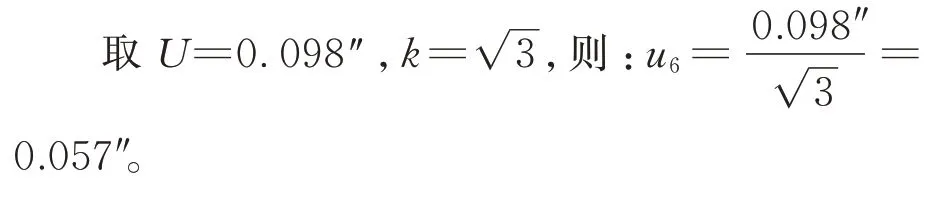
5.3 多面棱体安装调试过程引入的不确定度
使用谐波-神经网络组合补偿法时,要结合多组测量数据,需要在15°内转动多面棱体,该过程不改变自准直仪十字线的倾斜角度和多面棱体的平面度,但会改变多面棱体的倾斜状态。由5.2.3 可知,转动多面棱体引入的测角误差最大值为:
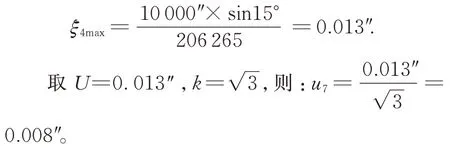
根据以上分析,使用传统方法补偿最终合成的不确定度为:
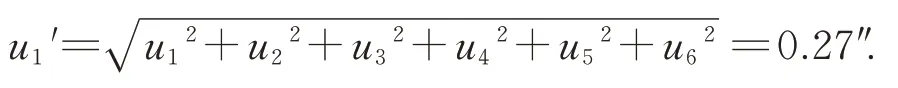
使用谐波-神经网络组合补偿法补偿合成的不确定度为:
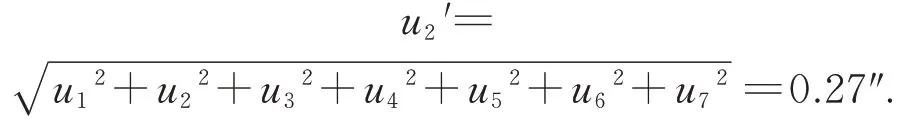
由结果可知,使用谐波-神经网络补偿法和传统方法补偿的合成不确定度均为0.27″,即在15°内改变多面棱体与圆光栅的周向相对位置不改变合成不确定度的大小。而且,改变多面棱体与圆光栅周向方向的相对位置所引入的测角误差最大值仅为0.013″,比标定系统总体测角误差小一个数量级,它对标定系统的影响可忽略不计,可视为等精度测量。
6 结 论
本文基于精密减速器检测仪的实际需求,提出了一种多数据关联的减速器检测仪测角误差拟合方法,将误差谐波法与BP 神经网络法结合起来,利用误差谐波法将多组角位置误差数据相关联,再带入BP 神经网络中训练拟合出圆光栅整周期测角误差。在误差谐波法的基础上再次对圆光栅测角误差进行补偿,编写了自动补偿程序,在分析现有圆光栅测角误差拟合方法的基础上,提高了减速器检测仪的测角精度。实验结果表明:谐波-神经网络组合补偿法修正后测角误差峰峰值为0.94″,标准差为0.25″,分别减小至误差谐波法修正后的33.3%和37.9%。该方法进一步提高了圆光栅的测角精度,使减速器检测仪的测角精度达到了亚角秒级别。

