侧向耦合分布反馈半导体激光器光栅结构及耦合特性
李瑞冬,邹永刚,田 锟,王 睿,范 杰,兰云萍
(长春理工大学 高功率半导体激光国家重点实验室,吉林 长春 130022)
1 引 言
分布反馈(DFB)半导体激光器因具有结构简单、良好的模式特性及稳定性等优势已经被广泛应用于激光通信、激光雷达以及泵浦光源等领域[1-4]。传统的DFB半导体激光器是基于掩埋式光栅制作而成[5],其器件制作过程中所必须的二次外延生长容易在波导材料中引入杂质,导致非辐射复合增强、散射损耗增加,造成半导体激光器温度升高、电阻增大等缺点[6-8]。为了降低器件的工艺难度,研究人员近年来逐渐对稳定性较好的折射率耦合型表面光栅DFB半导体激光器展开研究[9-11]。相对于脊波导表面光栅,将光栅刻蚀在脊两侧的侧向耦合脊波导(Laterally-coupled ridge-waveguide,LC-RWG)分布反馈半导体激光器可以实现电流的均匀稳定注入。2012年,英国格拉斯哥大学报道了一种具有弯曲锥形LC-RWG分布反馈半导体激光器,其中,光栅刻蚀深度与脊型高度相等,并在光栅中间部分引入四分之一相移,在实验中测得了耦合系数为24 cm-1,激光输出功率210 mW时线宽64 kHz,边模抑制比可达45 dB[12]。2017年,纽约州立大学石溪分校研制出耦合系数为1 cm-1、波长为3.22 μm的稳定单模LC-RWG分布反馈半导体激光器,并实现了15 mW的输出功率[13]。2018年,清华大学报道了一种1.3 μm光栅周期的LC-RWG分布反馈半导体激光器,其功率可达14 mW,边模抑制比能够达到40.8 dB[14]。
通常情况下,侧向耦合光栅比脊表面光栅耦合系数更小,其主要是由于侧向耦合光栅与光场分布之间的重叠(即光栅的光学限制因子)更小,所以需要增加刻蚀深度来补偿光栅的耦合系数。然而,高深宽比光栅不易制备且深刻蚀到有源区会导致损耗增加,容易对器件性能造成严重的影响[15]。同时,侧向耦合光栅的耦合系数对占空比等结构参数也较为敏感,光栅制作工艺的精度将显著影响半导体激光器的线宽、工作稳定性等特性。因此,设计并优化器件结构,实现对LC-RWG光栅耦合系数的合理调整具有重要意义。
通过设计侧向耦合光栅结构,可以在一定程度上减少工艺精度对光栅耦合系数的影响。本文基于耦合波理论和有限时域差分法研究了6种特殊侧向微结构光栅的耦合特性,分别是对称梯形、错位梯形、对称结形、错位结形、双对称梯形和双对称结形,模拟分析了特殊结构参数对光栅耦合系数的影响。
2 原理分析
耦合系数κ是LC-RWG分布反馈激光器设计与分析的一个重要参数。耦合系数描述了光栅对光波的反馈耦合程度,激光器谐振腔中的前向波和后向波的相互耦合越强,其耦合输出损耗越小,阈值增益越小[16]。根据耦合波理论,κ的一般表达式为[17]:
(1)
其中,k0是真空波矢量值,β是电磁波传播系数,E0是电场,Δε(x,y)是光栅引起的介电微扰。
对于掩埋异质结构光栅,普遍使用的标准公式为[18]:
(2)
其中,Гg是光栅区域中的光学限制因子,m是光栅的阶数,γ是光栅的占空比。公式(2)中用到了n1+n2≈2neff的近似值。但对于LC-RWG分布反馈激光器,公式(2)高估了耦合系数。另外,在使用公式(2)分析掩埋式光栅耦合系数时,忽略了光栅限制因子Гg随占空比γ的变化[18]。因为对于传统的掩埋式光栅,光栅限制因子Гg相对较小,横向光场分布不会随着占空比γ的变化而实质性改变。但对于LC-RWG分布反馈激光器,随着光栅结构参数的改变(包括占空比γ),横向光场分布会发生显著的变化,从而影响光栅限制因子Гg。因此,在分析和计算LC-RWG分布反馈激光器时,可将公式进一步优化如下[19]:
(3)
通过以上理论分析可知,光栅占空比γ对LC-RWG分布反馈激光器的耦合系数有着显著影响。光栅耦合系数与反射率具有如下关系[20]:
R=tanh2(κL),
(4)
其中,L为腔长。因此,本文基于以上理论分析特殊侧向微结构光栅结构参数对其反射率的影响,进而探究光栅结构参数与耦合系数的关系。
3 结果与讨论
本文基于有限时域差分法,针对GaAs基材料体系LC-RWG分布反馈激光器,模拟分析光栅结构参数与反射率的关系。首先建立矩形光栅结构模型,如图1所示。n型波导厚度1.5 μm,折射率3.32;有源层厚度0.4 μm,折射率3.35;p型波导厚度0.8 μm,折射率3.32。设定工作波长λ=980 nm,光栅周期1.475 μm,占空比γ=l/Λ=0.8,光栅与脊型区高度h=0.7 μm,脊宽w=1 μm,光栅侧向宽度s=2.5 μm。其耦合系数与反射率谱如图2所示。
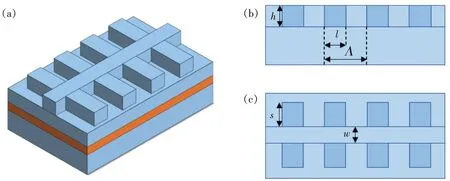
图1 矩形光栅结构示意图。(a)三维图;(b)侧视图;(c)俯视图。Fig.1 Schematic diagram of the rectangular grating structure.(a)Three-dimensional drawing.(b)Side view.(c)Top view.
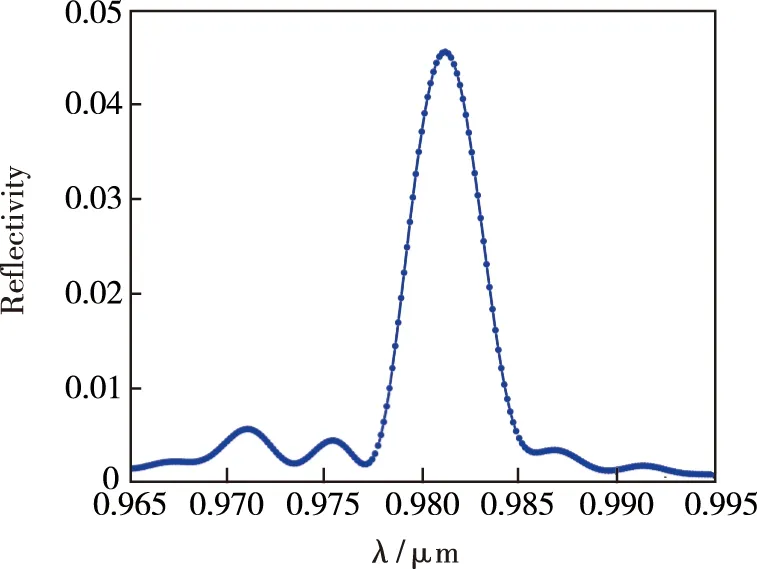
图2 矩形光栅反射率谱Fig.2 Rectangular grating reflectance spectrum
从图2可以看出,模型长度40 μm时矩形光栅结构的反射率约为0.046,耦合系数约为54.2 cm-1。为了适当地提高光栅的耦合系数,可以选择增大光栅占空比和刻蚀深度来实现。然而,局限于工艺上的微负载效应[21],高深宽比光栅不易制备。因此,我们设计了6种特殊侧向微结构光栅对上述结构模型的耦合系数进行调节,分别为一侧梯形对称的结构a、一侧梯形错位的结构b、一侧结形对称的结构c、一侧结形错位的结构d、两侧梯形对称的结构e和两侧结形对称的结构f,6种光栅结构的制备可通过ICP干法刻蚀实现。如图3所示,当6种光栅结构的侧壁纵向倾角θ同步发生变化时,相当于光栅沟槽宽度改变,等效占空比也随之改变。
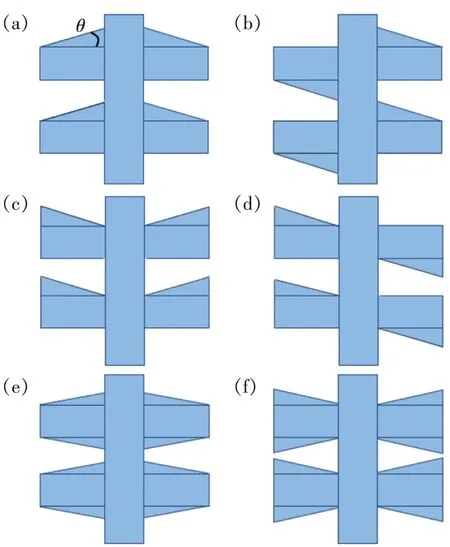
图3 6种不同结构的光栅俯视图。(a)对称梯形;(b)错位梯形;(c)对称结形;(d)错位结形;(e)双对称梯形;(f)双对称结形。Fig.3 Top view of gratings with six different structures.(a)Symmetric trapezoid.(b)Misaligned trapezoid.(c)Symmetric junction.(d)Misaligned junction.(e)Bisymmetric trapezoid.(f)Bisymmetric junction.
图4给出了6种结构的侧壁纵向倾角θ与耦合系数κ之间的关系。从图中可以看出,随着侧壁纵向倾角的增大,6种结构的耦合系数呈现出先升高后降低的趋势。侧壁纵向倾角增大,等效占空比随之增大,对于LC-RWG分布反馈激光器,其光栅区域的有效折射率也随之增大;同时,等效占空比增大,降低了光栅区域的光学对比度,进而使得更多的光能量进入光栅区域,从而提高了光栅区域中的光学限制因子及耦合系数。根据公式(3),耦合系数后续降低是因为等效占空比γ进一步增大,sin(πmγ)函数会呈现出先升高后降低的趋势。6种结构当中,结构b、d的耦合系数分别比结构a、c的耦合系数略高,是因为b、d两种结构可以类比于错位光栅,相同光栅间距下,错位光栅的占空比和光栅限制因子相对更高。结构c、d的耦合系数均比结构a、b的耦合系数更高,是因为c、d两种结构对等效占空比和光场分布的影响更大。较其余4种结构,结构e、f的耦合系数在更小的侧壁纵向倾角1°时达到最大值且数值更大,是因为e、f两种结构随着侧壁纵向倾角增大时,等效占空比增大的速率更快。a、b、c、d 4种结构和e、f两种结构侧壁纵向倾角分别在1.4°~2°和0.8°~1.2°之间耦合系数变化平缓,因此可以将结构设计在该侧壁纵向倾角之间,有助于减少工艺误差对耦合系数的影响。
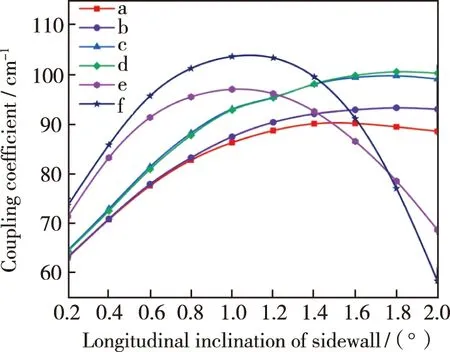
图4 6种结构的侧壁纵向倾角与耦合系数的关系Fig.4 Relationship between the longitudinal inclination of the sidewall of the six structures and the coupling coefficient
为了更好地分析这6种特殊微结构光栅的耦合特性,图5进一步研究了6种结构的侧壁纵向倾角θ与输出损耗之间的关系(损耗=1-反射率-透射率)。从图中可以看出,随着侧壁纵向倾角的增大,6种结构的输出损耗呈现出先降低后升高的趋势。值得注意的是,6种结构当中,e、f两种结构的损耗较其余4种结构波动较大,但最低损耗较其余4种结构更低且结构f在侧壁纵向倾角为0.8°时损耗仅为0.004 1。适当增大耦合系数,减小输出损耗,更有利于激光器获得更高的输出斜率效率。因此,在设计和制备激光器时,可以根据工艺参数和容差,选择适当的侧壁纵向倾角来避免耦合系数的波动、减小输出损耗、并保证耦合强度κL在一个合理的设计范围内,达到激光器性能稳定的需求。
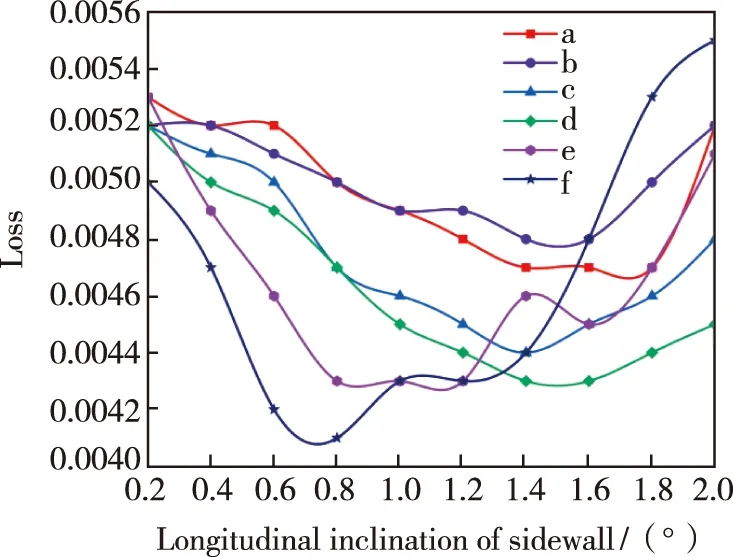
图5 6种结构的侧壁纵向倾角与输出损耗的关系Fig.5 Relationship between the longitudinal inclination of the sidewall of the six structures and the output loss
除光栅侧壁纵向倾角之外,脊波导光栅的其他结构参数(如脊宽、光栅侧向宽度以及占空比)的变动也会对其耦合性能产生影响。因此,选用输出损耗相对较低的结构f作进一步的模拟分析。
基于前文仿真获得的侧向光栅耦合调整方法和规律,我们针对器件(腔长为1 mm)的光栅进行了优化。将模型长度增大至100 μm,设置目标光栅耦合系数在10 cm-1左右。
图6给出了结构f的侧壁纵向倾角θ与光栅限制因子Гg之间的关系。从图中可以看出,当侧壁纵向倾角从0.2°增大到2°时,光栅限制因子也随之增大,证明了侧壁纵向倾角的变化是通过改变光栅限制因子来进一步影响耦合系数。
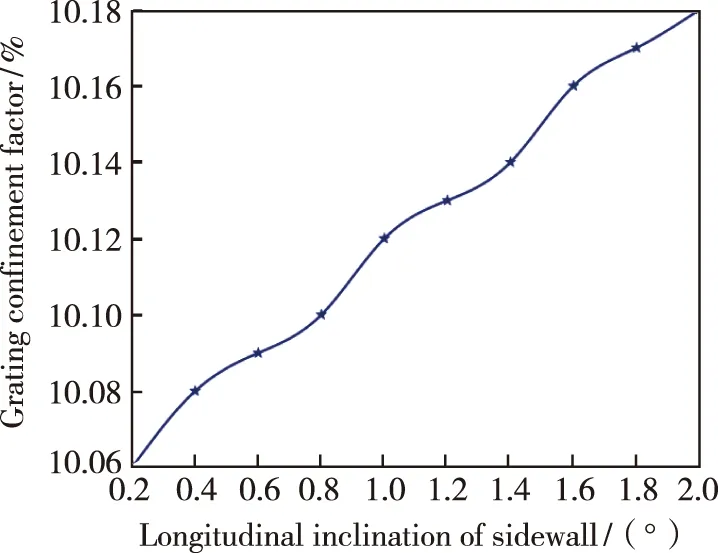
图6 结构f的侧壁纵向倾角与光栅限制因子的关系Fig.6 Relationship between the longitudinal inclination of the sidewall of the structure f and the optical confinement factor of the grating
图7给出了结构f的侧壁纵向倾角θ、脊宽w与耦合系数κ之间的关系。不同脊宽时,耦合系数与侧壁纵向倾角仍然满足图4中的关系。对于不同侧壁纵向倾角的特殊微结构光栅,当脊宽在1~3 μm增大时,耦合系数整体呈现出一个降低的趋势。脊形区宽度增大,光栅限制因子会不断减小,导致耦合系数降低。此外,当侧壁纵向倾角在0.2°~0.6°之间时,随着脊宽增大,耦合系数很快减小到饱和,这是因为光场被更多地限制在脊波导中,导致光栅限制因子不会进一步明显减小。当侧壁纵向倾角在1.6°~2°之间时,脊宽的变化对耦合系数的影响很小;同时,当脊宽在1.2~1.6 μm之间时,耦合系数会出现略微的波动。因此,在实际器件制备时,我们可以根据工艺条件来制备侧壁纵向倾角相对较大、脊宽在1.6 μm以上的特殊微结构光栅,不仅可以避免脊形区的刻蚀误差对耦合系数的影响,还可以避免脊宽太小导致的高电阻、输出功率低、腔内损耗增加等不利因素。另外,其余5种结构仿真结果与结构f有着相似的规律。
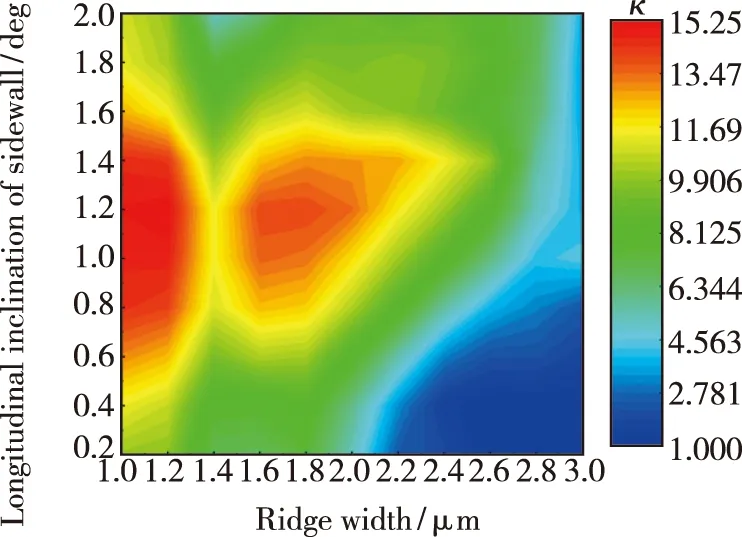
图7 结构f的侧壁纵向倾角、脊宽与耦合系数的关系(s=2.5 μm,γ=0.77)。Fig.7 Relationship between the longitudinal inclination of the sidewall of the structure f,the ridge width and the coupling coefficient(s=2.5 μm,γ=0.77).
图8给出了结构f的侧壁纵向倾角θ、光栅侧向宽度s与耦合系数κ之间的关系。当侧向宽度从2.5~3.5 μm增大时,耦合系数整体呈现出一个上升的趋势。侧壁纵向倾角越大,耦合系数随侧向宽度提高得越明显。侧向宽度的增大,使得光栅与光场的交叠区域增多,光栅限制因子与耦合系数升高。当侧壁纵向倾角低于1°时,侧向宽度对耦合系数的影响较小;而当侧壁纵向倾角高于1°时,光栅宽度对耦合系数的影响变大,尤其在1.4°~2°之间时,不同侧向宽度的耦合系数会出现明显的变化,高低耦合系数差值达到18 cm-1。因此,设计侧壁纵向倾角较低的特殊微结构光栅更有利于减小光栅侧向宽度刻蚀误差对耦合系数的影响。
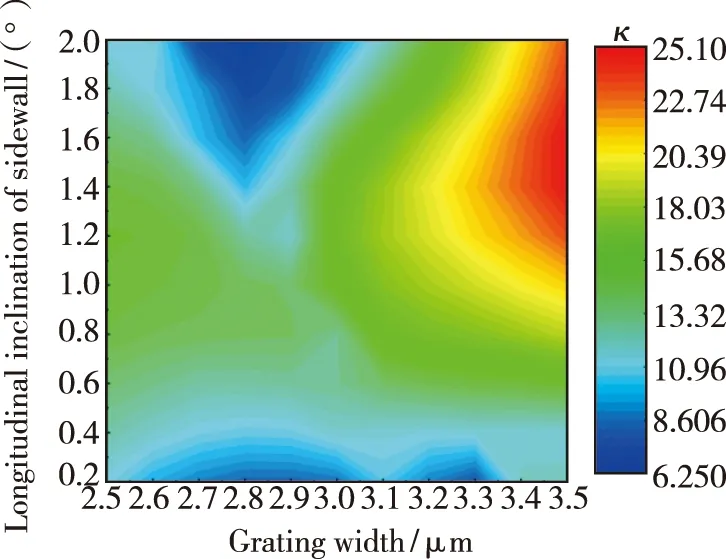
图8 结构f的侧壁纵向倾角、光栅侧向宽度与耦合系数的关系(w=1 μm,γ=0.77)。Fig.8 Relationship between the longitudinal inclination of the sidewall of the structure f,the lateral width of the grating and the coupling coefficient(w=1 μm,γ=0.77).
图9给出了结构f的侧壁纵向倾角θ、占空比γ与耦合系数κ之间的关系。不同侧壁纵向倾角下,随着占空比增大,耦合系数整体呈现出一个上升的趋势。侧壁纵向倾角越大,耦合系数随占空比提高得越明显。当占空比小于0.5时,侧壁纵向倾角对耦合系数的影响很小,高低耦合系数差值小于3 cm-1;而当占空比大于0.5时,不同侧壁纵向倾角的耦合系数会出现明显的变化,高低耦合系数差值达到11 cm-1。这表明,设计低占空比的特殊微结构光栅可以有效地降低耦合系数对侧壁纵向倾角的敏感度,有利于增加侧壁纵向倾角的工艺容差,降低工艺精度对特殊微结构光栅耦合系数的影响。
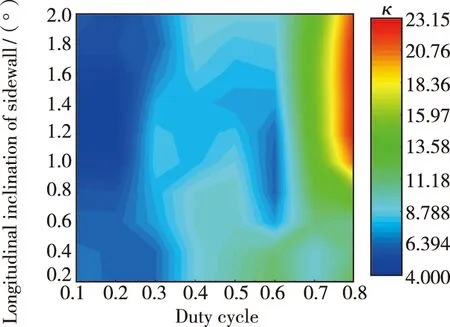
图9 结构f的侧壁纵向倾角、占空比与耦合系数的关系(w=1 μm,s=2.5 μm)。Fig.9 Relationship between the longitudinal inclination of the sidewall of the structure f,the duty cycle and the coupling coefficient(w=1 μm,s=2.5 μm).
4 结 论
本文在侧向耦合脊波导分布反馈半导体激光器的基础上,基于有限时域差分法对6种特殊侧向微结构光栅进行了模拟分析。研究结果表明,改变6种特殊侧向微结构光栅的侧壁纵向倾角能够有效地调节耦合系数以及输出损耗。当对称梯形、错位梯形、对称结形、错位结形4种结构和双对称梯形、双对称结形两种结构的侧壁纵向倾角分别在1.4°~2°和0.8°~1.2°之间时,6种结构的耦合系数变化平缓且输出损耗较低;根据仿真结果,双对称结形的侧壁纵向倾角分别在1.6°~2°和0.2°~1°之间时,能够有效地缓解脊型区高度和光栅侧向宽度的刻蚀误差对耦合系数的影响;同时,当光栅占空比低于0.5时,耦合系数对侧壁纵向倾角的敏感度很低,高低耦合系数差小于3 cm-1,这增加了光栅制作工艺的容差及侧壁纵向倾角设计的灵活性,并降低了制作工艺缺陷对光栅性能的影响。通过设计特殊侧向微结构光栅来调节耦合系数可以避免深刻蚀、高深宽比等复杂工艺,更易于器件的制作。

