EPS颗粒含量对混合土渗透性的影响*

叶文，黄林冲

1. 中山大学智能工程学院，广东广州 510006

2. 中山大学航空航天学院，广东深圳 518107

轻量土具有材料环保、质量轻和可调节土体密度等优点，因此被广泛应用于路基工程、桥梁工程和海堤工程等领域［1-4］。根据填充材料的不同，有发泡聚苯乙烯EPS（expanded polystyrene）混合轻量土、发泡颗粒混合轻量土、气泡混合轻量土、次生材料混合轻量土四类［5］，其中EPS混合轻量土的应用最为广泛。

众多学者针对轻量土的物理及力学性能展开了一系列的研究。在土体材料方面，研究表明：EPS颗粒与砂土、黄土、淤泥和棉秆纤维等材料混合后的轻量土具有良好的强度和稳定性［3，6-8］；在物理力学特性方面，主要是通过试验研究轻量土的性质，如：通过击实试验确定轻量土最优含水率和最大干密度［9］；通过室内动三轴试验研究轻量土的动强度参数［10］；通过无侧限抗压强度试验研究轻量土的密度、强度和变形特性［11］；在EPS颗粒掺量方面，研究表明：轻量土的动强度、抗压强度、弹性模量、抗剪强度、黏聚力、内摩擦角、最大循环应力比、初始压缩模量等随EPS颗粒掺入比的增大而减小［12-18］。以上研究表明，轻量土的力学性质与砂土类型及EPS 颗粒含量密切相关。

在某些工程中，如海绵城市建设，不仅仅要考虑轻量土的力学性质，还应考虑轻量土的渗透性。在一般情况下，轻量土的强度和渗透性两者关系相互矛盾，当土体孔隙率越大，对应的渗透性也越大，但是强度也变得更低。轻量土渗透性的主要影响因素有土体密实度、土颗粒的自身性质等。由于EPS颗粒的质量相对较轻，且具有较强的伸缩性，因此可通过控制EPS颗粒含量来改变土体密实度。目前，研究EPS颗粒含量对轻量土渗透性的影响主要是将EPS 颗粒、土颗粒和水泥混合、固结后研究其相关性质［19-20］。研究表明，对渗透性影响最大的是EPS 颗粒含量，其次是水泥的掺量。但是，EPS颗粒含量对混合土渗透性影响规律的研究尚显不足。本文通过河源石英砂、福建标准砂与EPS颗粒进行混合组成混合土，进行河源石英砂和标准砂在不同EPS颗粒含量情况下的渗透性试验，研究EPS颗粒对于混合土的物理性质及渗透性的影响。

1 试验材料及步骤

1.1 试验材料

本次试验选择的福建标准砂（以下简称标准砂）来自厦门艾思欧标准砂有限公司生产的中国ISO 标准砂，多为黄褐色，二氧化硅质量分数为96%以上。河源石英砂（以下简称石英砂）来自广东省河源市（以下简称石英砂），为天然石英砂，主要呈乳白色或无色半透明状，二氧化硅质量分数在99%以上，EPS颗粒的主要成分是聚苯乙烯树脂，多为圆球形，质量较轻。砂土颗粒及EPS颗粒如图1所示。

图1 砂土及EPS颗粒Fig.1 Sand and EPS particles

试验前，采用筛径为0.25 mm 和1.0 mm 的标准筛对石英砂和标准砂进行初步筛分，筛分后采用图像法测量石英砂、标准砂及EPS颗粒粒径，用排水法测量颗粒的密度。砂土和EPS颗粒的基本物理参数见表1所示。

表1 砂土和EPS颗粒的基本物理性质Table 1 Basic physical properties of sand and EPS particles

1.2 级配曲线及物理参数

颗粒形状是砂土的重要性质之一，不同的颗粒形态影响颗粒间的排列方式，而颗粒的排列方式是影响砂土密度的主要原因之一。本次试验随机选择少量石英砂、标准砂和EPS颗粒进行电镜扫描，观察砂土的颗粒形态。试验选用台式JSM-6010LA 型电镜，分辨率5.0 μm。砂土颗粒电镜图如图2所示，由图可以看出，虽然石英砂和标准砂的主要成分都是二氧化硅，但是颗粒形态存在较大的区别。石英砂颗粒形状较不规则，颗粒为长条形和薄片状，表面凹凸不平，存在明显的棱角，且颗粒大小差距明显。而标准砂颗粒形状较为圆润，颗粒大小均匀，颗粒表面棱角较少。EPS颗粒近似为圆球形，表面不存在棱角却存在微小的孔隙，因此受压的时候存在变形现象。

图2 砂土颗粒电镜图Fig.2 Electron micrograph of sand particles

对于室内试验，最常用的粒径统计方法是筛分法，其主要原理是用筛孔尺寸不同的筛对砂进行筛选，通过控制筛孔尺寸得到某一粒径等级的砂土，然后进行计算。筛分法具有设备及操作简单、试验材料较易获得等优点。但对于石英砂这种具有长条形颗粒，使用筛分法得到的级配曲线会存在较大的误差，且筛分法对不规则颗粒的筛分具有随机性，对颗粒的不同方向进行筛分，得出的结果也不同。对于渗透试验，粒径的分布情况将影响混合土的孔隙比，对试验结果产生较大的影响。对于颗粒材料，由于颗粒的几何形状不规则，因此不能单一用直径这一概念描述颗粒的尺寸，需将颗粒等效为与颗粒同体积的球形颗粒进行描述，这个球形的直径即为等效直径。为了能得到较为准确的颗粒粒径分布情况，本次试验采用图像处理方法对粒径进行统计，从而得到粒度分布情况。图像法的具体步骤如下：

（1） 随机选择5 组标准砂、石英砂和EPS 颗粒，将砂土颗粒平铺在纸上，为增加颗粒的对比度，本次试验选择砂纸作为背景。并将直尺放在砂纸的两个边缘，用于图像矫正和测量尺寸，并用相机拍摄图片，如图3（a）所示。

（2） 使用Fiji软件的测量功能，测量图片长和宽，得到图片的计算尺寸，并换算成以mm 为单位，如图3（b）所示。根据计算尺寸和实际尺寸的关系，确定图像的放大倍数，根据放大倍数进行图像矫正。

（3） 使用Fiji软件中的二值化功能，将目标图形二值化，然后选择计算区域，根据计算区域并选择软件中提取面积的功能选项，根据等效投影面积原理得到目标区域各个颗粒的面积并导出，如图3（c）所示。

图3 等效粒径计算Fig.3 Calculation of equivalent particle size

（4） 将导出的颗粒面积除以放大倍数，得到颗粒的实际面积，根据实际面积，换算成等面积的圆，这个圆的直径就是颗粒的等效粒径。

（5） 重新选取试样，重复步骤（1）～（4）。

试验总共选取标准砂颗粒样本1 334 个、石英砂颗粒样本1 156个、EPS颗粒样本409个。

根据图像法得到的粒径统计信息，绘制颗粒级配曲线，如图4所示。

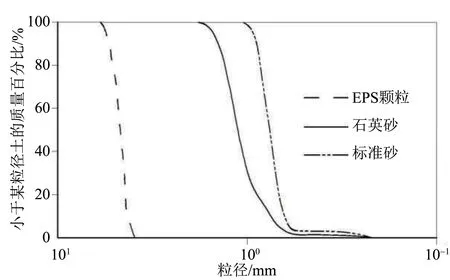
图4 颗粒级配曲线Fig.4 Particle gradation curve

1.3 试验步骤

渗透试验按照《土工试验规程》［21］设计。实验采用南京土壤仪器厂有限公司生产的TST-70 型常水头渗透仪。

因渗透仪所能容纳的试样质量并不确定，因此每次试验都制备总质量为3 000 g 的EPS 颗粒混合土。试验时，先按设计的配比分别计算好所需砂土和EPS 颗粒质量，并用电子称称取相应的质量，精确至0.01 g。由于EPS 颗粒质量很轻，很难充分搅拌均匀，且装样时颗粒易集中于试样上方，因此在试样中加入500 mL 水，并充分搅拌均匀，制成混合土，如图5所示。试样采用分层制样法制得，每次称取400 g 混合颗粒倒入圆筒内，为防止击实时受力不均匀，在混合土上部覆盖上薄铁片，并用击实器（内径φ61.8 mm）击实5 次，击实完成后取下铁片和击实器。最后一层装样后用刮刀刮去多余部分，使混合土保存在测压管上方4 cm处。为防止混合土被冲刷导致颗粒流失，在混合土上方铺上2 cm 厚的粒径为3 ～ 4 mm 的石英砂颗粒作为缓冲层。调节测压管水位高度，进行渗透试验并测量渗透系数。

图5 砂土-EPS混合颗粒Fig.5 Sand-EPS mixed particles

为消除温度影响，每次试验时分别测量进水口和出水口处的水温，取平均值作为试验温度，试验后计算试验温度下的渗透系数，按照换算关系统一修正为20℃水温时的渗透系数。试验结束后将剩余部分晾干，称量剩余EPS颗粒和砂土颗粒余量。每次试验重复3次，并求平均值。

根据剩余的EPS 颗粒、石英砂、标准砂的质量，计算实际用于试验的颗粒质量。并由颗粒密度，计算标准砂混合土、石英砂混合土的EPS颗粒体积百分比、相对密度、孔隙比，如表2所示。

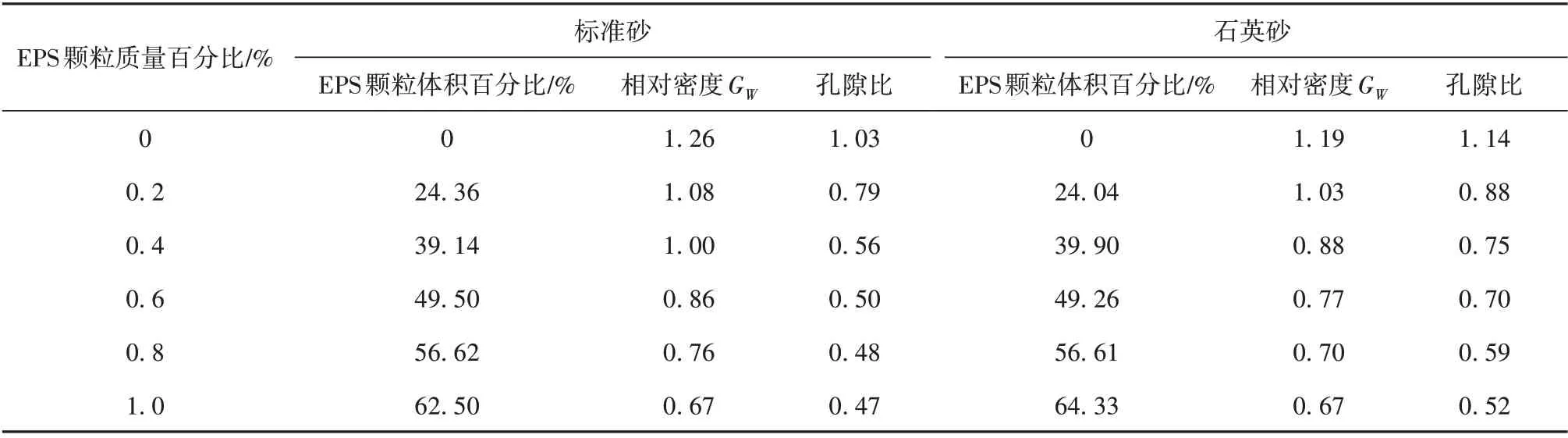
表2 混合土EPS颗粒体积百分比、相对密度和孔隙比Table 2 EPS particle volume ratio，relative density and porosity ratio of mixed soil

1.4 混合土物理参数

在对砂土的粒度分析中，不均匀系数反映颗粒粒度的范围，曲率系数反映了土的粒径级配累计曲线的斜率是否连续，平均粒径反映了混合土几何尺寸的尺度。不均匀系数和曲率系数的计算方法为：用孔径为0.25、0.3、0.5、0.6 和1.0 mm 的标准筛对石英砂和标准砂混合土进行筛分，并计算出过筛累积质量，然后算出质量比在10%、30%和60%时土的质量，根据筛分数据找出对应的质量在哪两个筛孔之间，最后用插值法确定质量比在10%、30%和60%时对应的粒径，即d10、d30和d60。不均匀系数Cu和曲率系数Cc定义为

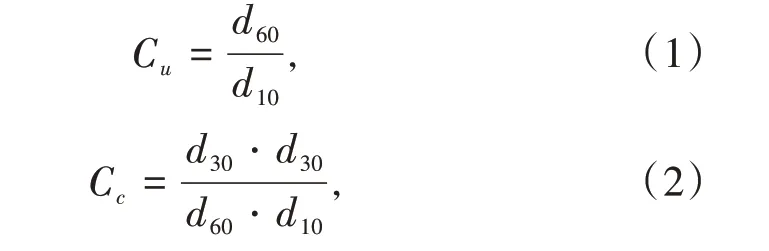
计算得到混合土的不均匀系数、曲率系数、平均粒径如表3所示。

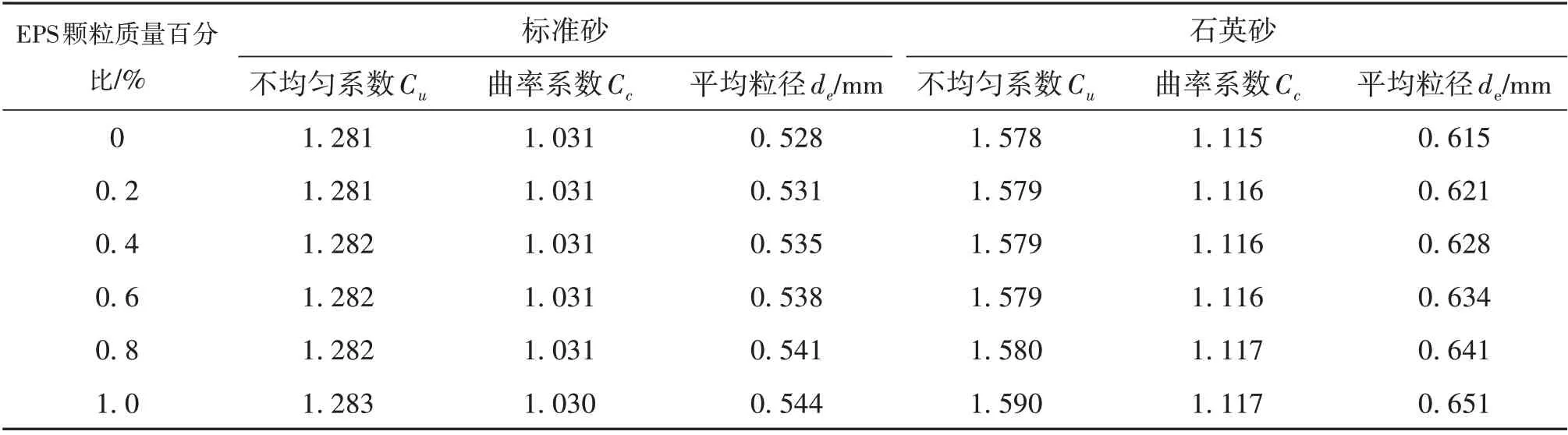
表3 混合土的不均匀系数、曲率系数、等效粒径Table 3 Unevenness coefficient，curvature coefficient and equivalent particle size of mixed soil

2 结果与分析

根据达西定律

其中A为过水断面面积，k20为渗透系数，Q为时间t内的渗透水量，L为两侧压孔中心间的试样高度，h为平均水位差。根据公式（3），计算得到不同EPS 颗粒含量（w）下混合土的渗透系数（渗透系数均为20 ℃时的渗透系数）如表4所示。

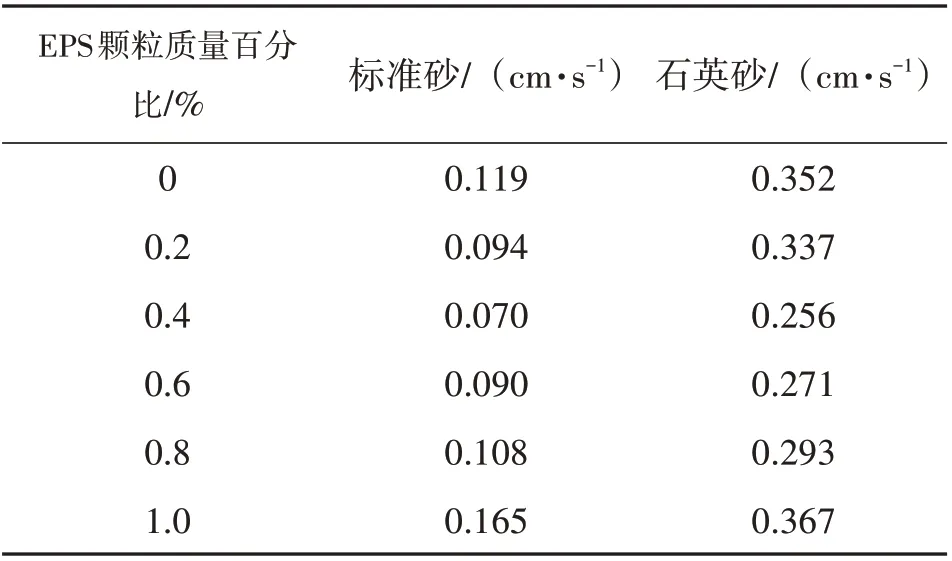
表4 不同EPS颗粒含量下混合土的渗透系数Table 4 Permeability coefficient of mixed soil with different EPS particle content

2.1 EPS颗粒含量对砂土物理性质的影响

轻量土重要的特点是减轻土体材料的质量，减轻质量最主要的措施是改变EPS颗粒的含量。但是，改变混合土中EPS颗粒含量的同时也改变了混合土的物理性质。因此，需要研究EPS颗粒与砂土混合后土体的密度、孔隙率等物理性质的变化情况。

图6 为EPS 颗粒质量百分比与混合土密度的关系。由图可知，混合土密度随EPS颗粒含量的增加线性减小，混合土中EPS颗粒的质量百分比每增加0.1%，密度减小约6%。由于EPS 颗粒具有极其小的颗粒密度，仅为0.015 8 g/cm3，是纯砂土堆积密度的0.6%左右。因此，EPS 颗粒在混合土中最主要的作用是降低土体密度。而石英砂和标准砂对混合土密度的影响差异性较小，同EPS 颗粒含量下，二者对应的混合土密度差距在5%以内。

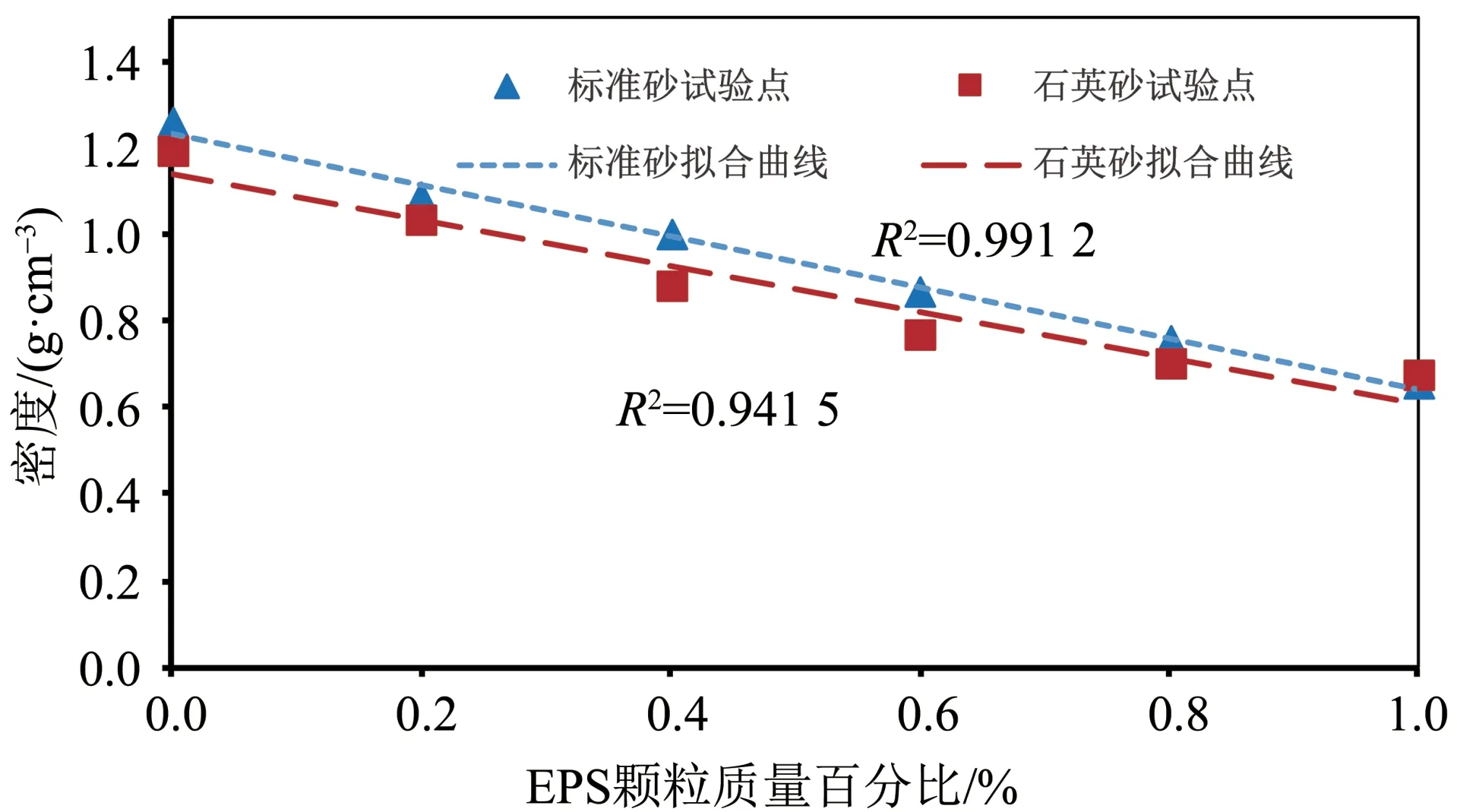
图6 EPS颗粒质量百分比与密度的关系Fig. 6 Relationship between mass ratio of EPS particles and sample density

图7 为EPS 颗粒占比与混合土孔隙率的变化情况。由图可知，混合土孔隙率随EPS含量的增加逐渐减小，但变化规律有较大的不同。石英砂混合土的孔隙率随EPS 颗粒含量的增加近似呈线性减小，EPS 颗粒含量每增加0.1%，石英砂的孔隙率减小0.8%。而对于标准砂混合土，混合土的孔隙率随EPS颗粒含量的增加呈二次函数关系变化，当EPS颗粒含量的体积占比达到50%后，混合土的孔隙率增长变得较为缓慢。因此，混合土随EPS颗粒含量的变化情况与其内部砂土的性质密切相关，其砂土颗粒尺寸较为均匀、形状较圆润时，混合土的孔隙率与EPS 颗粒含量近似呈二次函数变化；当砂土颗粒形状较不规则时，孔隙率近似为线性变化。所以，EPS颗粒对土体密度降低是有一定范围的。对于某些砂土，当EPS颗粒的体积占比达到50%（即质量比为0.6%）后，EPS 颗粒含量的提高对孔隙率的影响将变得很小。

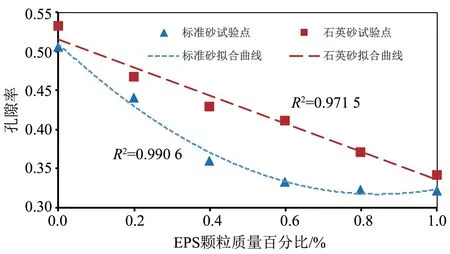
图7 EPS颗粒质量百分比与混合土孔隙率的关系Fig.7 Relationship between EPS particle mass ratio and sample porosity

结合表3 可得，不同EPS 颗粒含量的石英砂混合土和标准砂混合土的不均匀系数和曲率系数差距很小，可忽略不计；而平均粒径随EPS颗粒含量的增加缓慢增大。因此，影响混合土密度和孔隙率的最重要的参数是混合土的平均粒径。

2.2 EPS颗粒含量对渗透系数的影响

由前一节的分析可知，EPS 颗粒的含量将改变混合土的孔隙率，而砂土的渗透系数与孔隙率密切相关。本节通过拟合渗透系数与EPS 颗粒含量的函数关系，研究EPS 颗粒对渗透系数的影响。

2.2.1 EPS颗粒含量与渗透系数的关系根据表4，绘制混合土渗透系数与EPS 颗粒含量的关系曲线，如图8所示。由图可以看出，混合土的渗透系数与EPS 颗粒含量密切相关，随着EPS 颗粒的增多，石英砂混合土和标准砂混合土的渗透系数均先减小后增大，即呈二次函数规律变化。在相同的EPS 颗粒含量下，石英砂的渗透率比标准砂大3～10 倍。对比石英砂混合土及标准砂混合土，两者渗透率的不同主要与内部砂土的颗粒形状有关。石英砂颗粒相比于标准砂颗粒，颗粒更加不规则，导致石英砂颗粒间存在的孔隙比标准砂颗粒间多，因此渗透系数也就更大。

图8 EPS颗粒质量百分比与渗透系数的关系Fig. 8 Relationship between the mass ratio of EPS particles and the permeability coefficient

由上可知，EPS颗粒含量与混合土渗透系数密切相关，采用柯森-卡门［22］渗透公式进行进一步的研究。柯森-卡门渗透公式为

其中K为渗透系数，C0为无因次参数，n为孔隙率，de为平均粒径。由式（（4）得参数C0为

由表4及公式（5），得无因次参数C0与EPS颗粒含量的关系如图9 所示。若EPS 颗粒质量百分比为x%，C0与标准砂、石英砂混合土EPS 颗粒含量的拟合方程式分别为

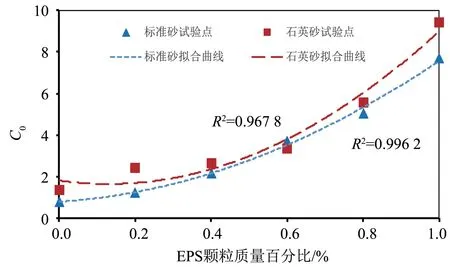
图9 C0与EPS颗粒质量百分比的关系Fig.9 Relationship between C0 and EPS particles mass ratio

由图9可以看出，参数C0随EPS颗粒含量近似成二次函数关系增长，且随着EPS颗粒含量的增加而增大，标准砂混合土对应的C0值均小于石英砂混合土。由拟合结果可知，河源石英砂混合土、标准砂混合土的C0值较为接近，渗透性系数不同主要是由混合土平均粒径及孔隙率造成的。

2.2.2 渗透系数模型计算根据砂土的渗透性理论，土体的渗透特性主要取决于砂土内部的孔隙体积特征和颗粒表面积特征。为了从微观角度分析土体的渗透特性，将土体内部抽象为等效渗透管，每根渗透管由EPS颗粒和砂土颗粒组成，如图10所示。

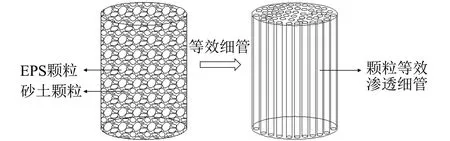
图10 土体渗透通道抽象示意图Fig.10 Abstract schematic diagram of soil infiltration channels

设所取土柱混合土的高为L，半径为rs，孔隙率为n，等效细管个数为N，每根等效细管的半径为r0，土柱过水面积上的平均流速为Vs，则根据土柱的总面积与细管面积之间的关系可得

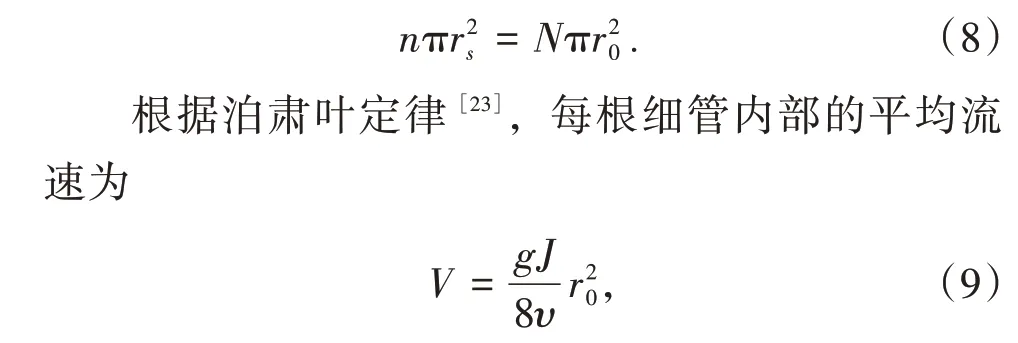
式中V为每根细管断面平均流速，g为重力加速度，J为水力坡降，υ为运动粘度。

设土体颗粒的平均直径为de，土颗粒数为Ne，则有

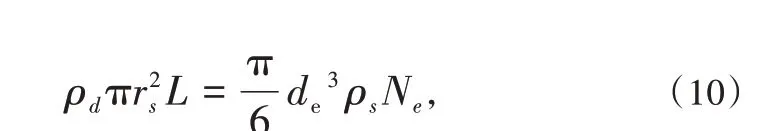
式中ρd为土体干密度，ρs为土颗粒密度。

砂土颗粒数量占比远多于EPS颗粒，因此颗粒间的接触形式主要为EPS 颗粒-砂土颗粒和砂土颗粒-砂土颗粒，如图11所示。

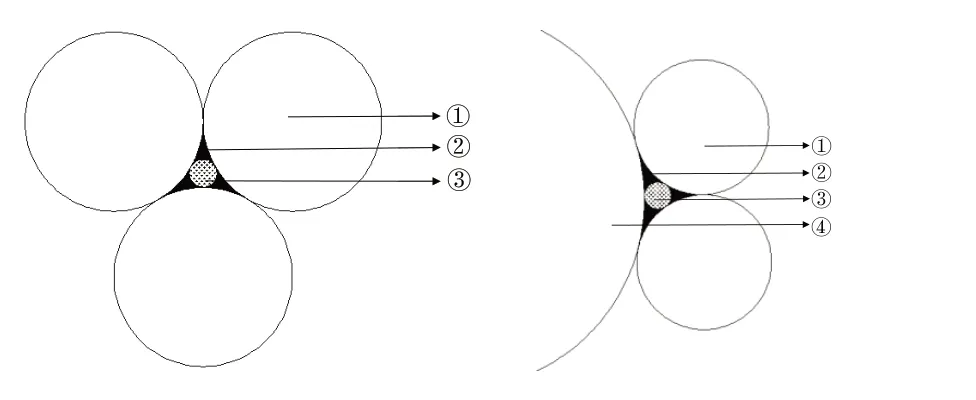
图11 颗粒接触形式Fig.11 Particle contact form

由于颗粒间紧密地接触在一起，颗粒间存在很小的缝隙，由于水的滞留作用使得这一部分产生水头损失。此外，将水流路径抽象为直管对渗透系数也存在折减作用。因此，引入叠合系数ξ表示这一部分损失。设等效细管的总面积为Se，土体颗粒的总面积为Sz，则

2.2.3 叠合系数与EPS颗粒含量的关系根据公式（4）和（15），C0和叠合系数ξ有

根据公式（5）～（16），计算得出叠合系数ξ随EPS颗粒质量百分比的变化如图12所示。

由图12，混合土中叠合系数随EPS 颗粒含量的增加线性减少。根据分析可知，砂土颗粒-砂土颗粒这类接触形式中的粘滞静止液体大于EPS 颗粒-砂土颗粒这一接触形式，即砂土颗粒-砂土颗粒具有更大的水头损失。因此随着EPS颗粒含量的增加，混合土中EPS 颗粒-砂土颗粒这一接触形式也增多，水头损失减小，抽象等效细管的管径增大，导致叠合系数减小。砂土颗粒形状对叠合系数在EPS颗粒含量较少时影响较大，随EPS颗粒含量的增多影响减小。

图12 EPS颗粒质量百分比与叠合系数的关系Fig.12 Relationship between EPS particle mass ratio and superposition coefficient

3 结 论

本文对不同EPS颗粒含量的石英砂混合土和标准砂混合土进行渗透试验研究，并结合柯森-卡门渗透公式，研究EPS颗粒含量对渗透性的影响，得出以下结论：

1）EPS 颗粒的密度仅为纯砂质量的0.6%。对于混合土，EPS 颗粒的质量每增加0.1%，密度减小约6%；当EPS 颗粒的质量占比为0.6%时，体积占比将达到50%，极大地提高了混合土的填充性能。

2）EPS 颗粒混合土的孔隙率随EPS 颗粒含量的变化情况与内部砂土的颗粒性质密切相关。颗粒尺寸较为均匀、形状较圆润时，孔隙率与EPS颗粒含量近似呈二次函数变化；对于颗粒较不规则时，近似为线性变化。对于标准砂混合土，当EPS颗粒的体积占比达到50%时，对孔隙率的影响将变得很小。

3）根据柯森-卡门渗透公式，研究发现：无因次参数C0与EPS 颗粒含量之间近似成二次函数关系增长，且随着EPS颗粒含量的增加而增大。标准砂混合土对应的C0值均小于石英砂混合土、但差异不明显，因此不同材料混合土渗透性系数的差异主要是由混合土平均粒径及孔隙率造成的。

4）通过等效细管模型，研究发现：混合土中叠合系数随EPS颗粒含量的增加线性减少。这主要是由于颗粒间的主导接触形式发生变化导致的。随着EPS 颗粒含量的增加，混合土中EPS 颗粒-砂土颗粒这一接触形式也增多，水头损失减小，抽象等效细管的管径增大，导致叠合系数减小。砂土颗粒形状对叠合系数在EPS颗粒含量较少时影响较大，随EPS颗粒含量的增多影响减小。

5）混合土的渗透系数随EPS 颗粒含量的增多呈二次函数变化的主要原因是：当EPS颗粒含量较少时，颗粒间占主导的接触形式是砂土颗粒-砂土颗粒，此时叠合系数较大，水头损失大，渗透系数的主要影响因素是混合土的孔隙率。随着孔隙率的减少，混合土允许通过的水量也较少，导致渗透系数随EPS颗粒含量的增加而降低；当混合土中EPS 颗粒质量占比增多至0.6%时，EPS 颗粒的体积占比将达到50%，此后孔隙率的变化将很小，而混合土占主导的接触形式是EPS 颗粒-砂土颗粒，此时叠合系数成为影响渗透系数的主要因素。随EPS颗粒含量的增大，叠合系数减小，水头损失也减小，混合土体允许流过的水增加，导致渗透系数增大。