基于模型预测的永磁同步发电系统控制

张昊清，魏 东

（1.北京建筑大学 电气与信息工程学院，北京 100044；2.建筑大数据智能处理方法研究北京市重点实验室，北京 100044）

0 引言

永磁同步发电机（PMSG）具有体积小、能量转换率高等优点[1]，通过原动机带动其旋转发电，经过机/网侧变流器整流逆变后并网[2⁃4]，可有效回收能源、提高能源利用率。但是，原动机受压力/风力等因素变化的影响，驱动转矩变化，导致转速不稳定，影响系统稳定运行，因此需研究相应的控制策略，提高系统稳定发电的能力。

目前系统中机/网侧变流器控制方法为直接转矩控制（DTC）与直接功率控制（DPC），DTC/DPC 方法会使得系统转矩、磁链或功率有较大的脉动[5]。针对该问题，文献[6]运用模糊控制器取代DPC 控制中原有的滞环比较器，实现了误差的精确调节，并建立了转子模型，控制了功率因数，提高了功率环的响应速度；文献[7]采用空间电压矢量调制（SVPWM）技术确定变流器的开关状态，以确保开关频率固定，抑制了传统DTC 控制中的转矩脉动问题，但SVPWM 与模糊控制方法计算量较大，无法实时保证控制精度；文献[8]设计了滑膜控制器，以磁链与转矩作为滑膜面进行控制，有效解决了定子磁链和转矩波动大的问题，同时还提高了系统响应速度，但滑膜轨迹易陷入死区，导致轨迹不可控，影响控制效果。

模型预测控制（MPC）具有原理简单、实现方便、响应效果好等优点，与DTC/DPC 方法相结合能够改善系统的动态性能[9]。但目前系统工作时机/网侧变流器通常独立运行[10]，当原动机驱动转矩变化时，网侧控制部分无法及时反馈机侧参数的变化，造成网侧电压响应速度较慢，导致母线电压波动较大，系统动态性能变差。

本文利用MPC 方法对永磁同步发电系统传统DTC/DPC 方法进行改进，机侧变流器采用模型预测直接转矩控制方法（MPDTC），网侧变流器采用模型预测直接功率控制方法（MPDPC），并在此基础上将机侧输出功率反馈给网侧母线电压控制外环，实现机/网侧变流器一体化控制，以降低母线电压与有功功率的脉动。

1 系统结构

永磁同步发电系统结构如图1 所示。系统通过原动机（在压力能回收中为膨胀机，风能回收中为风力机等）+永磁同步发电机+机/网侧变流器的结构回收能源并进行发电并网。机侧变流器调节发电机的电磁转矩，保持发电机转速稳定；机/网侧中间并联母线电容用于稳压；网侧变流器调节有功功率维持直流母线电压稳定，并减小输出电流谐波率，提高电能并网的输送效率，图中Tm为驱动转矩。

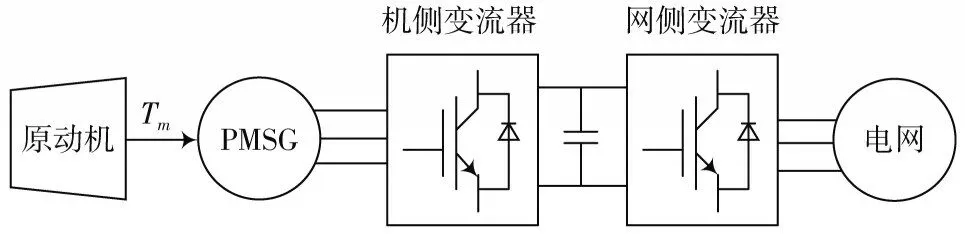
图1 永磁同步发电系统结构

2 系统数学模型

MPC 算法以预测模型为基础，因此需建立永磁同步发电系统的预测模型，模型分为两部分，分别是机侧变流器MPDTC控制部分与网侧变流器MPDPC控制部分。

2.1 机/网侧变流器数学模型

根据基尔霍夫定律，在同步旋转dq坐标系下建立永磁同步发电机数学模型[11]如下：

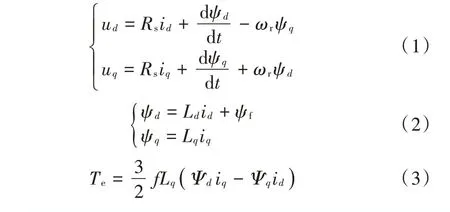
式中：Rs为定子电阻；ud，uq，id，iq，Ψ d，Ψ q分别为定子电压、电流、磁链在同步旋转dq坐标系上的两个分量；Ψf为转子永磁体磁链；Ld，Lq分别为定子d，q轴电感；ωr为转子角速度；f为电机极对数。

根据基尔霍夫定律建立网侧变流器数学模型为：

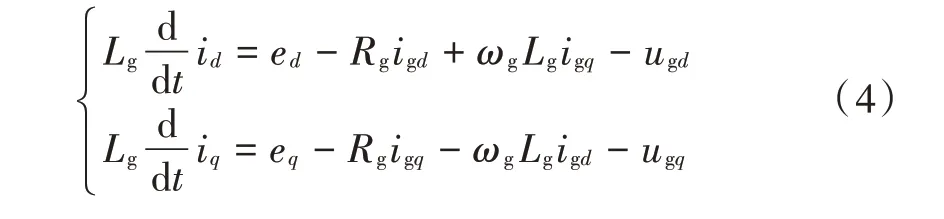
式中：Lg，Rg为网侧滤波电感与电阻；igd，igq为电网电流在dq坐标系下的分量；ed，eq为电网电压在dq坐标系下的分量；ωg为电网电压角频率；ugd，ugq为网侧变流器电压在dq坐标系下的分量。

2.2 机/网侧变流器预测模型

根据式（1），式（2），可得到发电机定子磁链状态方程：

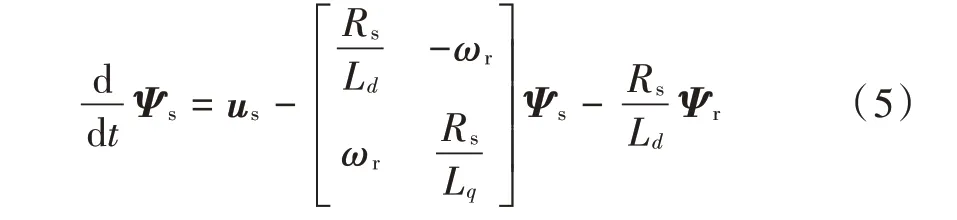
式中：Ψs=[Ψ d Ψ q]T；us=[ud uq]T；Ψr=[Ψr0]T。

根据前向欧拉离散法对式（5）进行离散化，得到永磁同步发电机定子磁链预测模型：

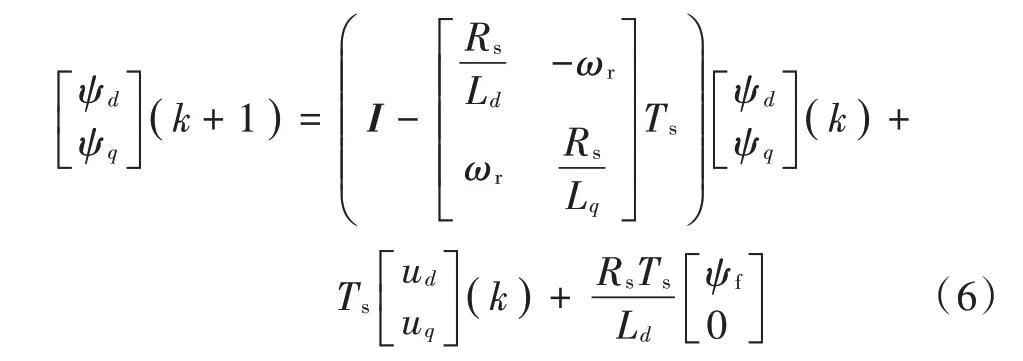
式中：I为单位矩阵；Ts为控制周期。

同理，可得电机定子电流预测模型：

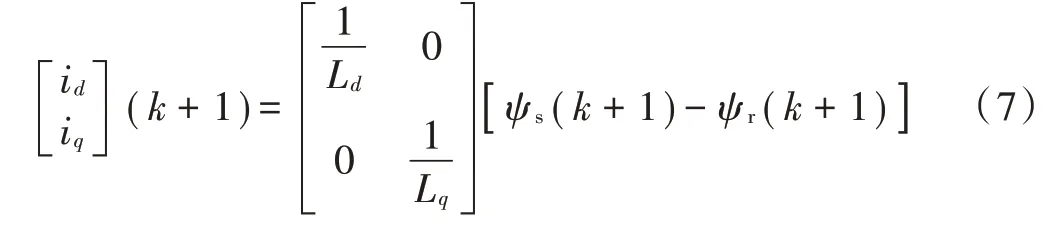
再根据式（6），式（7）得到电磁转矩预测模型：

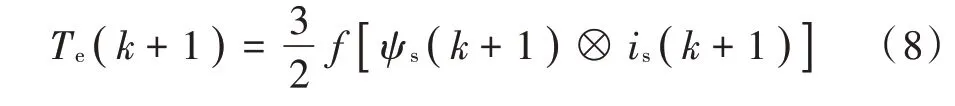
式（6）～式（8）为机侧部分磁链、电流与转矩的预测模型。

由式（4）可得有功/无功功率的表达式为：

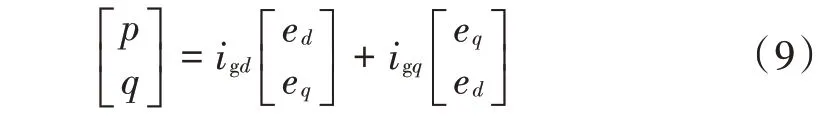
式中：p，q为网侧有功、无功功率。对式（9）求导，并根据前向欧拉离散法进行离散化，得到有功/无功功率的离散数学表达式：

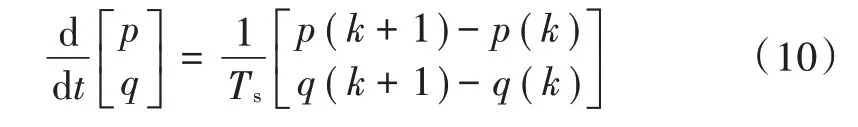
式中：p(k+1)，q(k+1)为k+1时刻网侧有功、无功功率。

将式（9）代入式（10）中，可得：

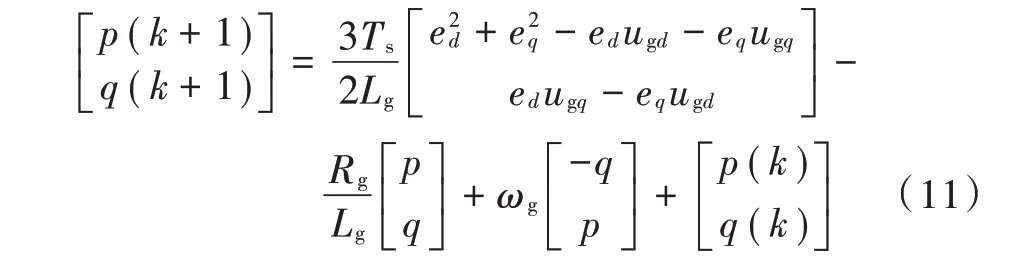
式（11）为网侧有功/无功功率的预测模型。

3 永磁同步发电系统MPC 方法

永磁同步发电系统MPC 结构如图2 所示。

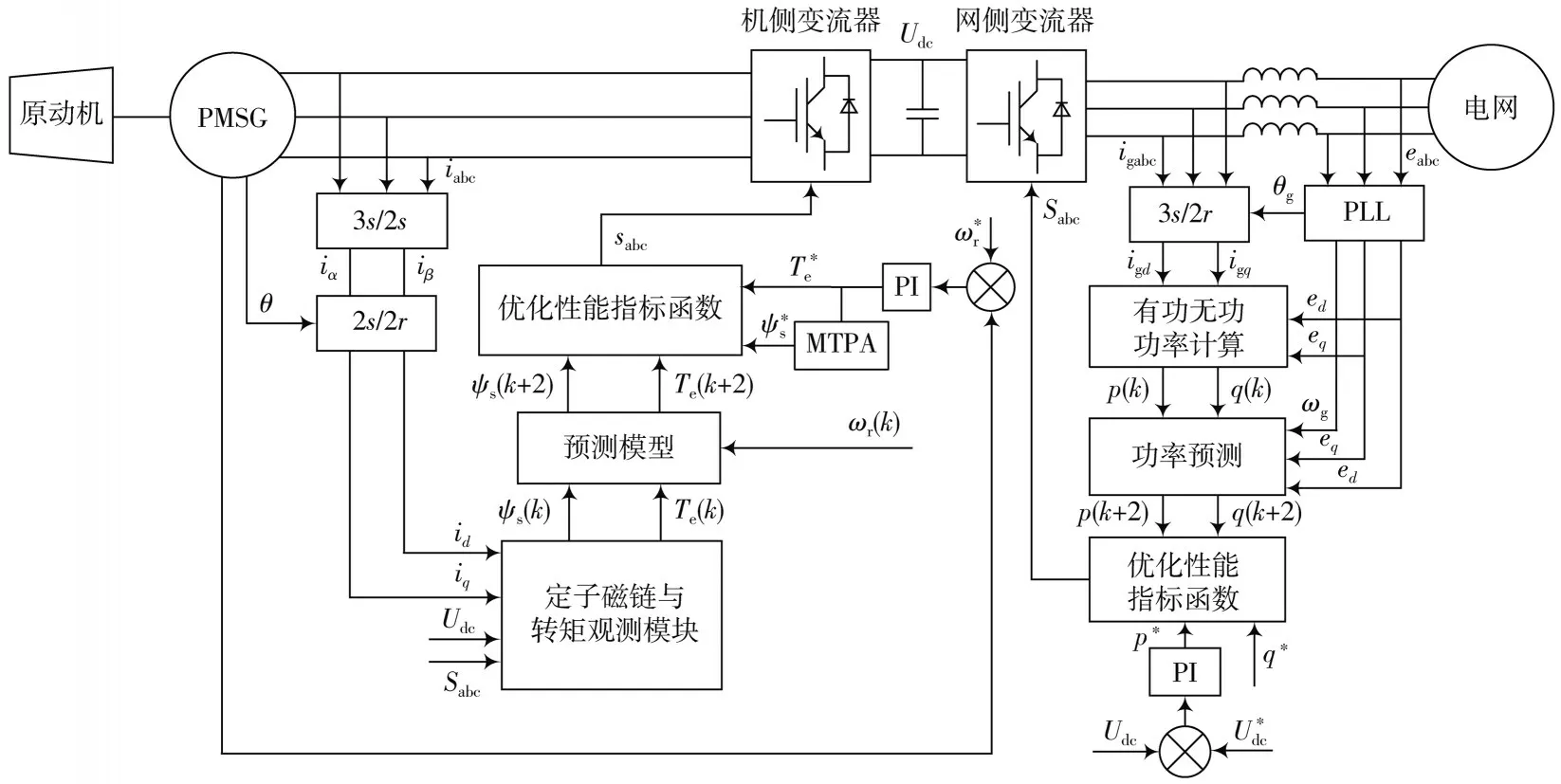
图2 永磁同步发电系统MPC 结构

3.1 机侧变流器MPDTC 方法

MPDTC 控制算法外环为转速环，内环利用模型预测控制器取代传统DTC 控制中的滞环比较器与开关矢量表，通过建立转矩、磁链和功率的预测模型，将减小上述状态变量与其设定值之间的偏差作为优化目标。在预测时域内对不同电压矢量作用下转矩和磁链的变化轨迹进行预测，并对优化目标函数进行评估，选择使预测时域内整体目标函数最优的电压矢量输出，从而降低转矩与磁链的脉动，改善系统动态性能。

对于发电机系统，每个控制周期算法流程的实施都要消耗一定时间，导致输出电压矢量时发电机相关参数已经发生变化，因此需进行延时补偿[12]，在k+1 时刻的基础上预测下一时刻的参数值，即预测时域为两步，对应的部分预测模型表达式为：

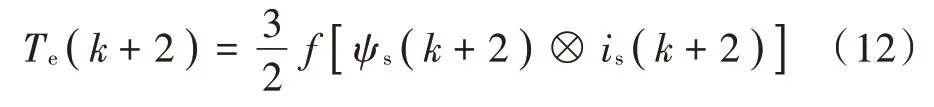
MPDTC 方法的控制目标是在系统原动机转矩波动时保持发电机转速稳定，降低转矩与定子磁链脉动，因此本文选择电磁转矩、磁链与其设定值之间的平方误差作为优化目标函数：

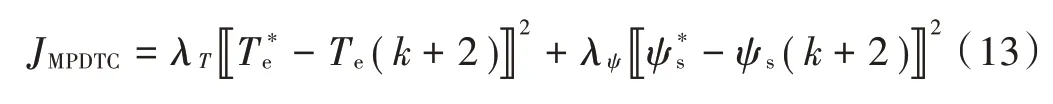
式中λT，λψ分别为转矩项和磁链项的权重系数。

3.2 基于机侧功率反馈的网侧MPDPC 方法

与MPDTC 控制方法类似，MPDPC 也由双闭环控制系统组成，外环为电压环，维持直流母线电压稳定。传统MPDPC 方法根据检测到的直流母线电压与其设定值之间的偏差，经过PI 控制后得到有功功率设定值，但是这种方法在原动机驱动转矩出现波动后，母线电压变化时才改变功率设定值，使得网侧系统无法对转矩波动进行及时反应，导致网侧母线电压与功率出现脉动。从图1可以看出，功率在发电机与电网之间通过双PWM 变流器与母线电容双向流动，当原动机驱动转矩变化导致机侧系统参数变化时，根据功率守恒关系，可得：

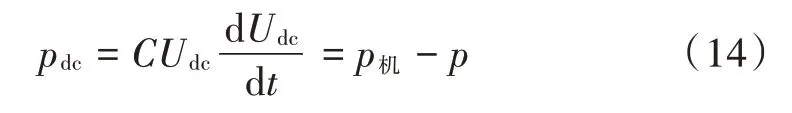
式中：C为母线电容；Udc为直流母线电压；pdc为母线电容功率；p机为机侧输出功率；p为网侧有功功率。

由式（14）可以看出，当驱动转矩波动时，若要使母线电压稳定，则需要保持机/网侧功率的动态平衡，因此，本文将机侧变流器的输出功率直接反馈给电压控制环，当驱动转矩波动时可根据机侧功率变化实时改变网侧有功功率的设定值，以提高系统动态响应速度，降低母线电压与功率的脉动。MPDPC 电压控制外环结构如图3 所示。图3a）为传统母线电压PI 控制外环结构，图3b）为机侧输出功率反馈的电压控制外环结构。

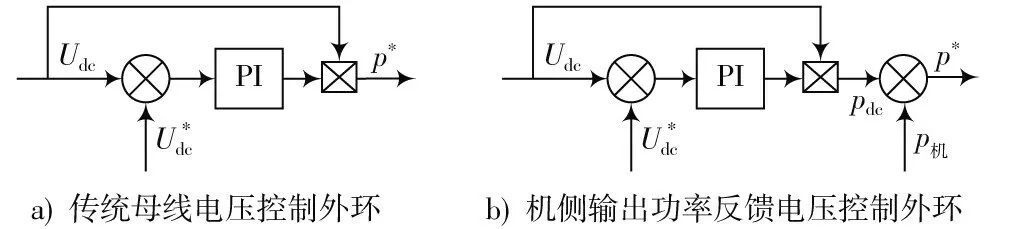
图3 电压控制外环结构

传统母线电压控制外环有功功率设定值为：

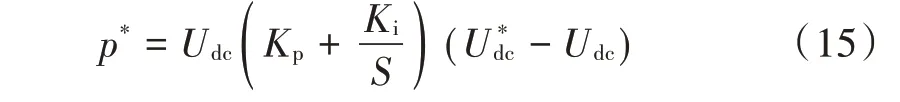
根据以上分析，基于机侧输出功率反馈的电压控制外环有功功率设定值为：

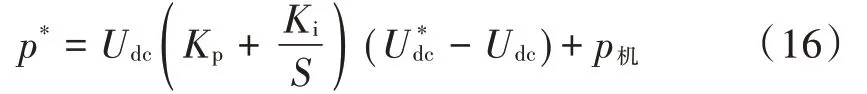
式中：p*为网侧有功功率设定值；为母线电压设定值。

k+2 时刻网侧有功与无功功率的预测模型表达式为：

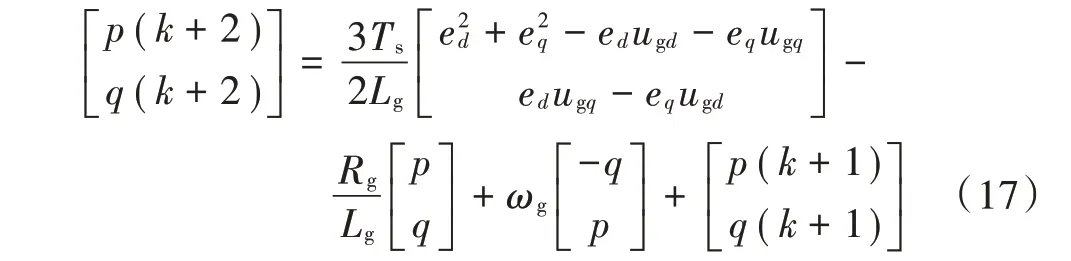
MPDPC 方法通过控制有功/无功功率保持母线电压稳定，因此选择有功、无功功率与其设定值之间的平方误差作为MPDPC 方法的优化目标函数：

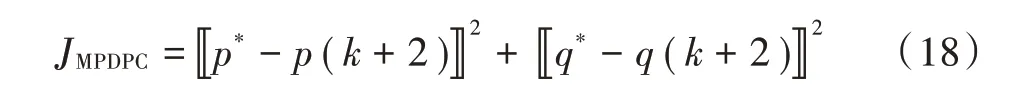
4 仿真实验

为验证上述控制策略的有效性，本文在Matlab/Simulink中建立永磁同步发电系统模型，模型参数见表1。

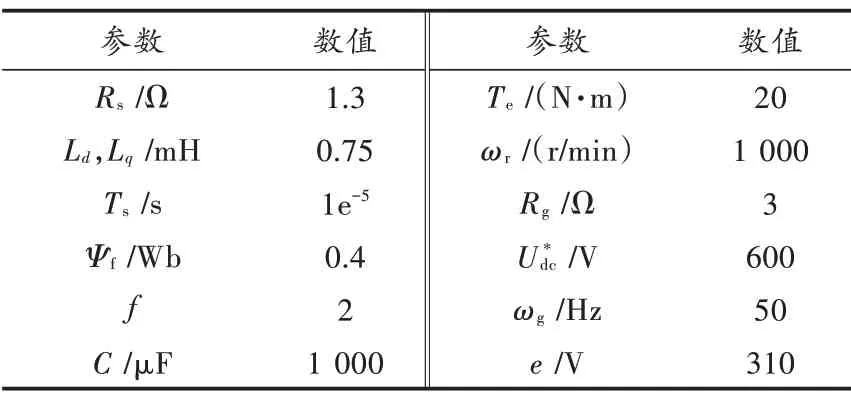
表1 系统模型参数

在0.2 s 时调整原动机驱动转矩从16.5 N·m 阶跃至21.5 N·m，模拟原动机受压力/风力等因素影响驱动转矩突变。

图4 为机侧MPDTC 控制算法与传统DTC 控制算法各参数控制效果对比图。图4a），图4b）为两种算法转速波形对比图，图4c），图4d）为转矩对比图。

由图4 中可以得出，两种算法在原动机驱动转矩突变的情况下都可以使发电机转速稳定，MPDTC算法在转矩突变情况下转速的波动在20 r/min左右，约0.02 s恢复稳定，且稳态时转速波动很小，并且可以很好地追踪驱动转矩的变化，转矩脉动在±1 N·m 左右；DTC 算法转速波动为50 r/min，稳定状态下转速波动在±15 r/min 左右，约0.04 s 稳定，转矩脉动为±6 N·m，相比DTC 算法MPDTC 算法转速波动降低60%，转矩脉动降低75%，响应速度提高50%。

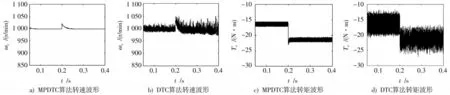
图4 机侧两种算法各参数控制效果对比图

图5 为传统MPDPC 算法各参数的控制效果图，图5a）为母线电压波形图，图5b），图5c）为有功、无功功率波形图，图5d）为电流THD 波形图。从图5 中可以看出，当原动机驱动转矩波动时，传统MPDPC 算法可以维持母线电压稳定，能够根据转矩波动调节有功功率，无功功率保持在设定值0 附近上下波动，并且电流输出正弦度较高，谐波率较小，为2.12%，但电压外环没有实时反馈机侧功率的变化，因此当驱动转矩突变时网侧母线电压与有功功率波动较大，且有一定的超调。

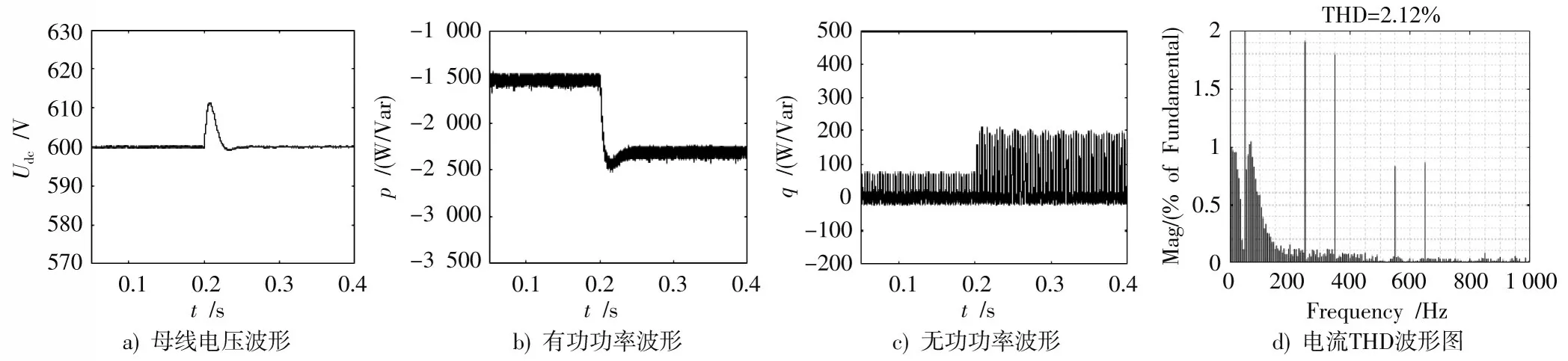
图5 网侧传统MPDPC 算法各参数控制效果图

图6 为机侧功率反馈的MPDPC 算法（图中为改进MPDPC 算法）与传统MPDPC 算法各参数控制效果对比图。图6a），图6b）为两种算法母线电压波形对比图，图6c），图6d）为有功功率对比图。从图6 中可以看出，基于功率反馈的MPDPC 控制算法在驱动转矩波动时母线电压的幅值为3 V，约0.02 s稳定，而传统MPDPC算法为10 V，响应时间为0.04 s，基于功率反馈的MPDPC 算法有功功率脉动在±15 W 左右，几乎没有超调，而传统MPDPC 算法脉动在±60 W 上下，超调量为50 W，相比传统MPDPC算法，基于功率反馈的MPDPC 算法母线电压波动降低70%，响应速度提高50%，有功功率脉动降低75%。

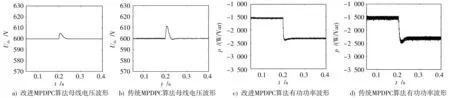
图6 网侧三种算法各参数控制效果对比图

5 结语

针对永磁同步发电系统传统DTC/DPC 方法中转矩与功率脉动大的问题，采用MPC 方法进行改进，并将机侧输出功率直接反馈给网侧母线电压PI 控制外环，根据机侧功率变化提前确定网侧有功功率设定值，使网侧系统能够及时对原动机驱动转矩波动进行反应。通过与传统控制方法对比，得到以下结论：

1）基于MPC 方法的永磁同步发电系统控制方法相比传统控制方法，可以很好地追踪原动机驱动转矩的变化，使发电机系统转速稳定，维持直流母线电压稳定，并且输出电流谐波率低，系统发电质量较高；

2）基于机侧功率反馈的网侧MPDPC 方法相比传统MPDPC 方法在驱动转矩波动时可以有效降低母线电压与有功功率的幅值，提高系统响应速度。