一种减小F⁃OFDM系统PAPR的改进算法

林志阳

（海南大学 信息与通信工程学院，海南 海口 570228）

0 引言

正交频分复用（Orthogonal Frequency Division Mul⁃tiplexing，OFDM）采用多载波调制技术，具有抗多径衰落和抗窄带干扰能力而广泛应用于4G 网络[1]。但OFDM 系统的主要缺点在于高峰均比（Peak⁃to⁃Average Power Ratio，PAPR），高PAPR 不仅影响系统的整体性能且在接收端产生高功耗[2]，为此，学者们提出了新型的载波调制和频谱网络切片技术的子带滤波正交频分复用[3⁃6（]Filtered⁃OFDM）系统模型。F⁃OFDM 技术能合理分配系统的带宽资源，允许通过增加子带滤波器扩展循环前缀（Cyclic Prefix，CP）长度和减少数据流所占系统的空间。但F⁃OFDM 技术[7]是将带宽划分为多个子带，当子载波数增加时，经离散傅里叶逆运算（Inverse Discrete Fourier Transform，IDFT）之后，所有的子载波相加导致发射功率放大器和数模转换器的信号量化噪声比增加，使系统产生较高的PAPR。

采用选择映射法[8（]Selective Mapping，SLM）能够有效地降低系统PAPR，不足在于，需要多次离散傅里叶逆变换生成候选信号集，使得系统复杂度大大增加。文献[9]对SLM 方法进行改进，其主要思想是通过生成转换矩阵（Conversion Matrices，CM）取代离散傅里叶逆运算来降低系统的复杂度，然而CM 方法采用穷举搜索方法且需要额外的插入操作，会导致候选信号具有较高的相关性，使系统性能降低。

遗传算法（Genetic Algorithm，GA）采用随机搜索方法，能有效降低系统的PAPR[10]，为此，本文提出了一种改进的SLM⁃GA 方法来降低F⁃OFDM 系统的PAPR 以满足未来5G 通信的需求。

1 F⁃OFDM 系统模型

F⁃OFDM 系统是将输入的数据划分为若干个子带，在经过16QAM 调制技术前进行串/并（Serial to Parallel，S/P）转换，通过IFFT 和加CP 后传递给子带滤波器，最后测量PAPR 再通过信道进行传输。F⁃OFDM 系统如图1所示。

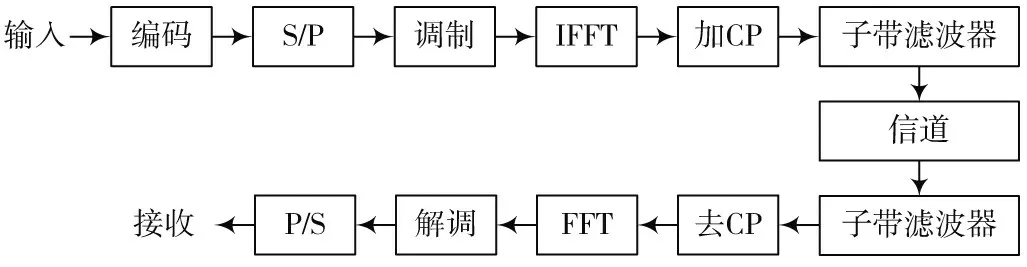
图1 F⁃OFDM 系统框图

对于n个F⁃OFDM 信号的过采样时域信号，表示为：

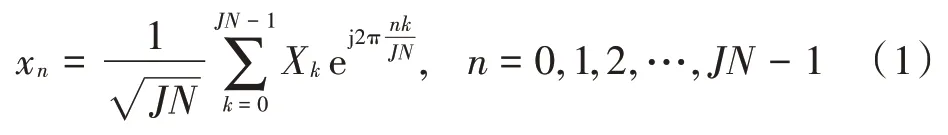
式中：J表示过采样率，当J≥4 时，可表示为逼近连续时间信号的峰值；N表示采样点；JN表示子载波的数量；Xk表示第k个子载波符号。

时域F⁃OFDM 系统的PAPR 表示为：

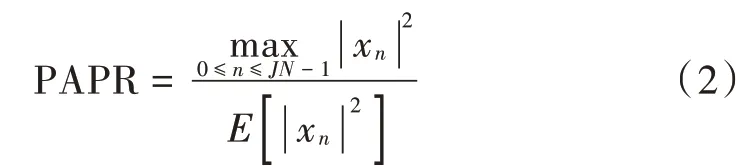
式中E表示平均功率。

互补累积分布函数（Complementary Cumulative Dis⁃tribution Function，CCDF）表示为：

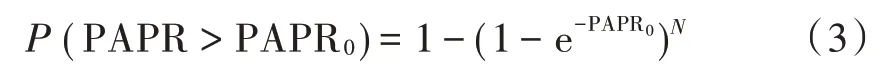
式中PAPR0表示门限值。

2 改进SLM⁃GA 算法分析

传统的SLM 方法是将原始的F⁃OFDM 符号乘以M组相位旋转因子，得到M组相同信息的统计独立序列，最后选择PAPR 最低的序列进行传输。

对于M组候选信号表示为：

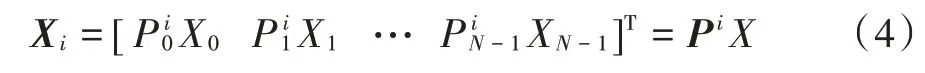
式中：Pi表示相位旋转矩阵，表示第i个随机生成相位∈[0,2π]，i=0,1,2,…,M-1，n=0,1,2,…,N-1；X表示N个等带宽的独立子载波。

对于时域F⁃OFDM 信号表示为：

式中：Q表示JN×JN矩阵经过IFFT 后生成元素qn,k=。对于第i个候选信号采用SLM 方法表示为：

将式（5）变换后代入式（6），则：

令Gi=QPiQ-1，由卷积性质可知，时域信号xi的循环卷积表示为F⁃OFDM 的时域信号和相位旋转向量的IFFT，则通过简单的循环卷积可替代复杂的乘法运算[11]，因此，式（7）可表示为：

为了降低计算机复杂度，本文采用的SLM⁃CM 方法生成的候选信号满足条件为：非零元素的数量限制为4 个；非零值分别设置为{±1,±j}，此时，只需计算3JN的加法运算，而不需要乘法运算。

图2给出了改进的SLM⁃GA算法原理图，可以看出与传统SLM 算法相比，需要额外的变异插入操作，文献[11]通过转换矩阵中的非零值之间的零元素等操作生成备选的候选信号：

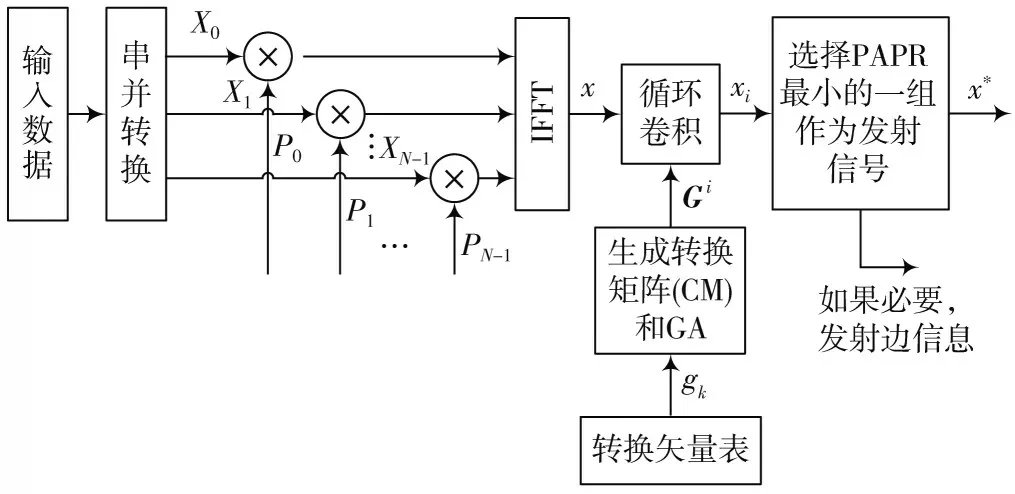
图2 改进的SLM⁃GA 算法原理图

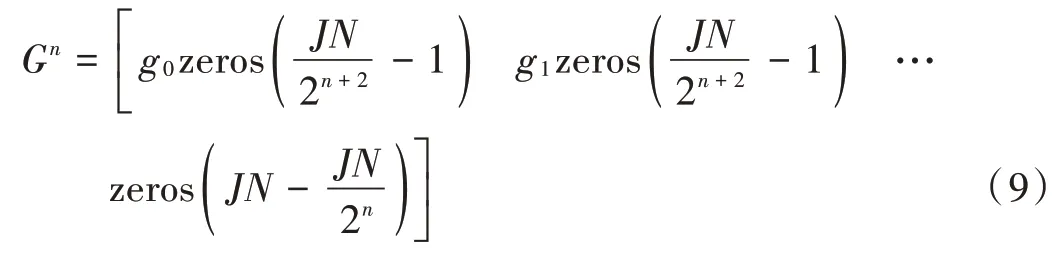
式中：n=0,1,2,…,log2(JN4)；gk表示转换矢量表中的非零值；zeros(m)表示m个零元素的行向量。

为了生成最优CM，本文采用GA 算法，通过每个染色体的非零值遗传编码和空间参数进行搜索[11]。

对于第i个二进制编码的染色体Ci，表示为：

式中：aR=[a1a2…ar]，ar∈(0,1)表示{±1,±j}中可能的非零值；bS=[b1b2…bs]，bs∈(0,1)表示gk中可能的零点数。

通过GA 算法后，式（9）的CM 表示为：

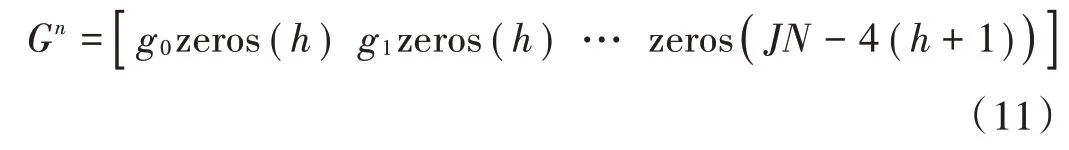
式中h∈(0,JN4 -1)。

根据文献[12]，CM 的适应度函数值（Variance of Correlation，VC）的相关性和方差表示为：

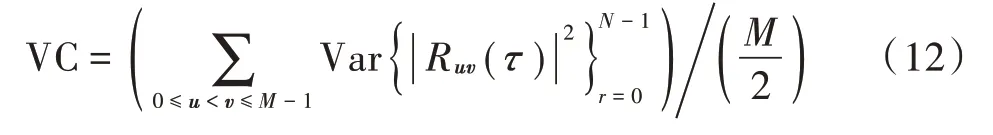
式中：Var{·}表示方差；Ruv(τ)表示任意两个转换矩阵u和v之间的相关性。

改进的SLM⁃GA 算法基本思想如下：

1）初始化：种群大小D、交叉概率Pc、变异概率Pm、设置迭代次数L。

2）生成初始种群：D染色体由随机的二进制位和转化矩阵中的非零值距离表示。

3）计算适应度函数值：每条染色体中的转换矩阵由二进制编码非零值和距离信息表示。根据文献[12]，若染色体的转换矩阵不在集合内，则计算与转换矩阵对应的第i个适应度值，其中i=1,2,…,D。

4）生成下一代种群。将适应度值最高的D2 双亲染色体和子染色体组合，生成新的种群。

5）变异和交叉：通过改变随机的二进制位对新的种群进行变异和交叉。

6）如果最大迭代次数L没有达到最大值，则返回步骤2）；否则，转至步骤7）。

7）结束：通过转换向量的循环下移获得最优循环转换矩阵。

3 仿真分析

为了验证本文算法的有效性，将其与SLM 算法[9]以及SLM⁃GA 算法[10]对比。假设F⁃OFDM 系统采用子载波N=128，调制方式为16⁃QAM，过采样率J设置为4，SLM算法的随机相位集设置为∈{0,π2,π,2π}，GA 算法的种群大小D=32，交叉率、变异率和最大迭代次数分别为：Pc=0.7，Pm=0.05 和L=100。图3 为本文算法与SLM⁃CM 算法和SLM⁃GA 算法比较，当互补累积积分函数CCDF=10-2时，本文采用的算法比传统算法减少约0.5 dB，其主要原因是只使用一次IFFT 运算，降低了系统复杂度。在高斯白噪声信道中，系统的误帧率或误码率性能比较如图4 所示，由图可知，本文采用的算法在性能上明显优于其他算法。

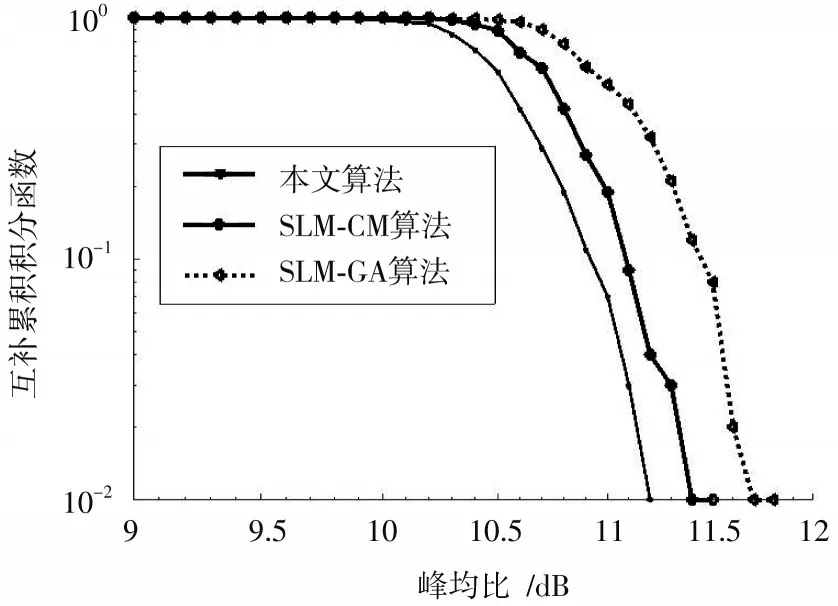
图3 不同算法下的峰均比

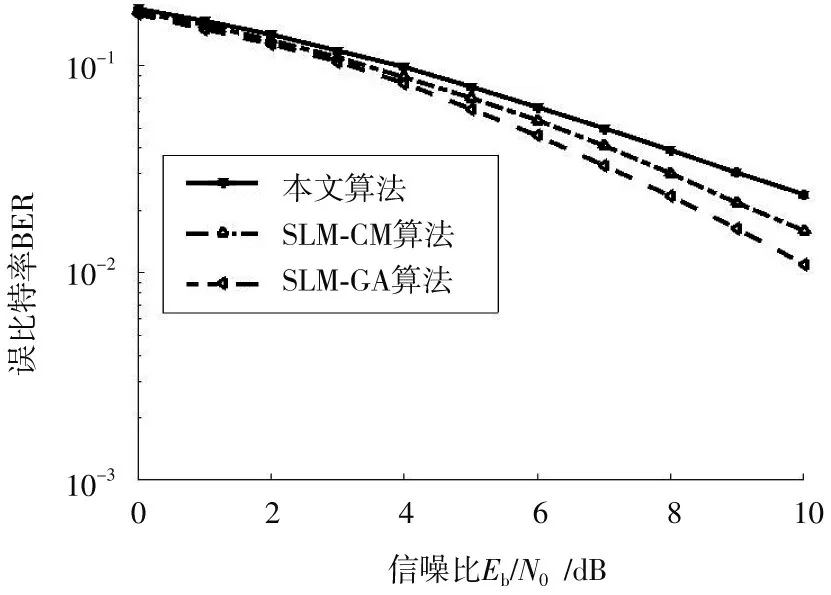
图4 不同算法下的信噪比

随着子块数目M的增加对系统性能的影响[13]，如图5 所示，仿真结果表明本文采用的算法不仅降低了PAPR，还减少了计算复杂度，有效提高了系统的性能。

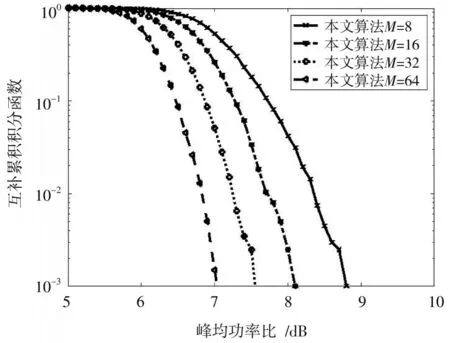
图5 不同子块的峰均比比较

为了再次验证本文采用算法的优越性[13⁃14]，分别比较了不同算法的迭代次数，如图6 所示。若子载波数为128，迭代次数为60时，本文算法峰均功率比约为4.84 dB，比SLM⁃CM 算法少约0.44 dB，比SLM⁃GA 算法少约1.05 dB，当迭代次数达到100 时，本文算法比SLM⁃CM 算法减小约1.09 dB。说明随着迭代次数的增加，本文采用的算法明显优于SLM⁃CM 方法。

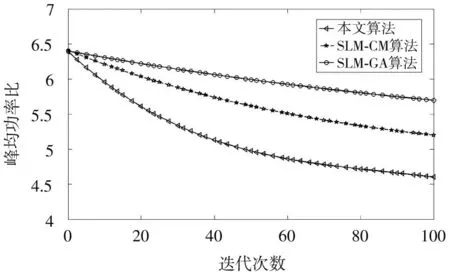
图6 不同算法迭代次数对比

4 结语

本文采用基于GA 的SLM⁃CM 算法，减小了F⁃OFDM系统的PAPR，通过GA 算法优化候选信号集和相关参数。结果表明，本文采用的方法在PAPR 值减小、系统性能和复杂度计算上明显优于对比方法，但该方法未能达到理想情况，仍需要做进一步优化。