基于互惠性约束的可解释就业推荐方法
朱海萍 赵成成 刘启东 郑庆华 曾疆维 田 锋 陈 妍
(西安交通大学电子与信息学部 西安 710049) (智能网络与网络安全教育部重点实验室(西安交通大学) 西安 710049)
近年来,随着推荐系统的广泛应用,就业推荐在辅助大学生就业方面逐渐起到重要作用[1].但是,相比于一般的推荐场景,就业推荐除了需要考虑学生对于就业单位的兴趣,还需要考虑就业单位对于学生的能力要求[2].课题组发现,若忽略了就业单位对学生能力的要求,很可能导致学生与推荐的单位之间出现“能力失配”问题.同时,在就业推荐过程中,推荐结果的解释信息对于指导老师和学生都具有重要的参考价值.然而,当前大多数基于隐因子模型(latent factor model, LFM)来实现协同过滤[3](collaborative filtering, CF)的方法通常缺乏解释性.负样本不置信问题(即训练数据中的负样本通常从大量未交互样本中随机采样得到[4])是推荐系统研究中一个普遍存在的问题[5],而在就业推荐数据中一个用户只有其就业单位一条交互记录,使得该问题更加严重.为了解决上述问题,本文开展基于互惠性约束的可解释就业推荐研究.
首先,借鉴文献[6]中拥有相似特征的人倾向于做出相似行为的结论,本文设计了一种基于相似度的随机负采样模块,即根据学生间和就业单位间的相似度从一个学生的负样本全集中划分出与其较为不相似的负样本集;再从该缩小范围的负样本集中,随机采样得到高置信度的负样本,结合已有正样本形成高质量训练样本集,从而提供数据级有效支撑.
其次,为了满足可解释性需求,分别设计2个可解释模块:1)借鉴意图决定行为这一心理学研究成果[4],设计基于就业意图的可解释模块,用以提升推荐系统的解释性;2)考虑到不同单位对学生能力要求的侧重点不同且不同学生对单位期望的侧重点也不同,设计基于就业特征的可解释模块,输出单位特征和学生特征的重要性分数,以此支撑推荐结果的可解释.
然后,基于上述可解释性输出,设计基于互惠性约束的就业推荐模块,以缓解推荐结果可能出现的“能力失配”问题.关键在于,因为对不同的学生和就业单位来说,就业兴趣和单位能力要求的重要程度是不同的,使用模糊门机制自适应地聚合两者的表征向量.
本文所提基于互惠性约束的可解释就业推荐方法的主要贡献有4个方面:
1)所提随机负采样模块,综合考虑学生间和单位间相似度,破解了负样本不置信问题.
2)所提2个可解释模块,综合运用多任务学习、注意力机制、门控网络,兼顾就业特征和就业意图演化过程,满足了推荐结果的可解释需求.
3)提出了基于互惠性约束的就业推荐模块,其特色在于,采用模糊门机制自适应地聚合学生就业兴趣和单位能力要求的表征向量,缓解了“能力失配”问题.
4)在某高校5届毕业生就业真实数据集(employ-ment data for undergraduate, EMDAU)上的实验结果表明:相比于多个经典和同时代的推荐方法,本文所提出的基于互惠性约束的可解释就业推荐方法在AUC指标上超出6%;且通过用户调研,验证了所提方法可解释性的有效性;设计并执行针对以上3个模块的消融实验,实验结果证明了其有效性.
1 相关工作
本节主要概述与本研究相关的就业推荐、互惠推荐以及可解释性推荐的研究现状.
1.1 就业推荐
现有的就业推荐算法通常根据历史用户的就业记录,使用隐因子模型构建基于协同过滤的方法,为用户推荐有潜在兴趣的就业单位[3].但是,CF算法本身是基于用户的历史记录来进行推荐的[7-8],而在一般的就业数据中每个用户只有其最终选择的就业单位这一条交互记录,因此不能直接使用CF算法.针对该问题,一些就业推荐研究重点关注用户相似度计算的方法.文献[9]提出使用基于语义的方法,从用户递交的简历中提取出其求职能力等结构化信息,利用这些结构化信息可以计算出用户之间的相似度;文献[10]则引入了学生画像,首先根据毕业生在校数据生成学生画像,然后利用毕业生学生画像计算毕业生相似度,从而进行就业单位推荐;文献[11-12]利用学生在校数据将学生划分为不同的群体,将个人所在群体的历史就业记录作为个人历史就业记录使用CF算法,解决了毕业生因缺少历史就业记录而难以使用CF算法的问题.
现有的就业推荐算法研究大多集中于研究学生就业兴趣建模,而本文同时对就业单位能力要求进行了建模.由于通过计算学生相似度来更好地使用CF算法进行就业推荐不是本文的研究重点,因此本文仅使用学生的各类属性特征作为其协同过滤特征.
1.2 互惠性推荐
互惠推荐系统(reciprocal recommender systems, RRS)[13]是一类需要最大化成功匹配概率而非只满足推荐对象偏好的推荐算法.Xia等人同样针对在线约会场景,提出了基于协同过滤的互惠推荐模型[14].该模型通过被推荐用户与和目标用户交互用户的相似度来计算2个单向偏好分数,然后将这2个偏好得分的谐波平均值作为2个用户之间匹配可能性的互惠得分.RCF已经成功应用于在线约会场景,并且成为RRS的标准对照算法[15-16].除了在线约会场景,互惠推荐还有一些其他的应用场景,比如社交网络[17]和技能分享平台[18]等.
当前,互惠推荐主要应用于社交推荐场景当中.而本文将互惠推荐的思想引入到就业推荐场景中,为就业推荐模型设计了互惠性约束,满足了在就业推荐中同时考虑学生就业兴趣与单位能力要求的需求.
1.3 可解释性推荐
可解释推荐(interpretable recommendation)因其有助于提高推荐系统的透明度、说服力、可信度等,得到了研究者们更多的关注[19-20].现有可解释推荐按照可解释模块与推荐模型是否相关,可被分为两大类:模型可知的可解释推荐与模型未知的可解释推荐.模型可知的可解释推荐,可解释模块嵌入在推荐模型当中,推荐结果与对推荐结果的解释是同时由模型输出的,如EFM模型[21].模型不可知的可解释推荐,又称为后处理方法,该类方法单独设计一个解释模型,输出推荐结果之后再由解释模型输出对该推荐结果的解释,如DualPC模型[22].按照解释结果的信息源分类,可解释推荐方法可被分为三大类:基于相关用户或物品的、基于特征的和基于文本的.基于相关用户和物品的方法是将与目标用户相似的其他用户或者目标用户之前交互过的一些物品作为当前推荐物品的解释,如Xian等人提出的EX3模型[23].基于特征的方法通常以物品特征的重要程度作为解释信息,如Hou等人[24]使用物品特征重要性的雷达图来解释为什么推荐某一物品.基于文本的方法通常生成对推荐物品的评价作为解释信息,如Wang等人[25]设计用户偏好建模与评论内容建模的多任务模型,输出预测的用户评论用以解释推荐结果.
虽然解释信息对于就业推荐有着重要的作用,但是现有就业推荐研究很少涉及可解释性.本文为了满足就业推荐可解释这一亟待解决的实际需求,提出了基于就业意图和就业特征的可解释推荐模块.
2 基于互惠性约束的可解释就业推荐方法
基于互惠性约束的可解释就业推荐方法整体结构如图1所示,图中实框是基于相似度的随机负采样模块,用于提供高置信度的负样本,再结合已有正样本形成高质量训练样本集D;通过嵌入层从样本集D中抽取高阶的特征向量表示;点框内包含基于就业意图和基于就业特征的2个解释模块,提供推荐结果的解释;虚线框内是基于互惠性约束的就业推荐模块,输出针对某一学生的被推荐单位评分.本节将详述这3个模块.
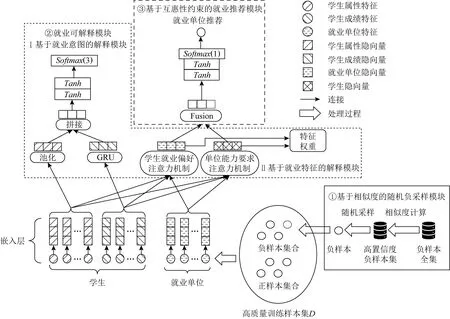
Fig.1 A framework of reciprocal-constrained interpretable job recommendation method
2.1 基于相似度的随机负采样模块
针对就业推荐数据中的负样本不置信问题,本文受同一学生群体在就业选择上相似这一想法启发,设计并实现了基于相似度的随机负采样模块,包括学生间相似度计算与就业单位间相似度计算、基于相似度的随机采样2个步骤.
1)在借鉴文献[26]相似度计算方法的基础上,本文设计学生间相似度和单位间相似度的计算:
(1)
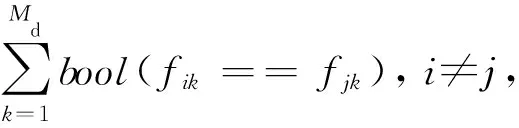
(2)
其中,sim(stui,stuj)表示学生stui和stuj之间的相似度,Nd和Nc分别表示学生的离散特征和连续特征的个数,fk表示第k个特征的值.sim(uniti,unitj)表示就业单位uniti和unitj之间的相似度,Md表示就业单位的离散特征的个数.
2)为了得到高置信度的负样本,同时避免严重改变训练集的样本分布,本文提出在考虑相似度的同时还保留随机采样的方法.首先计算学生u与其他学生的相似度以及学生u的就业单位与其他就业单位的相似度,选取最不相似的TopN个学生的就业单位和最不相似的TopN个单位作为高置信度负样本集.然后从该负样本集中随机采样,产生用于训练的负样本.
基于相似度的随机负采样计算伪代码如算法1所示:
算法1.基于相似度的随机负采样算法.
输入:学生集合studentSet、就业单位集合unitSet;
输出:负样本集合negativeSet.
①negtiveSet=[];
② forstuiinstudentSet
③sims=[],simu=[];
④uniti=get_unit(stui);/*获取学生交互的单位*/
⑤ forstujinstudentSet
⑥simij=sim(stui,stuj);/*调用式(1)计算学生间相似度*/
⑦sims.add(simij);
⑧ end for
⑨unsims=TopN(sims);/*按相似度从小到大排序,获取最不相似的N个学生*/
⑩ forunitjinunitSet
2.2 就业可解释模块
该模块包含基于就业意图的解释模块和基于就业特征的解释模块,分别从不同角度为推荐结果提供解释.
2.2.1 基于就业意图的解释模块
借鉴就业意图决定就业行为这一心理学研究成果[27],及文献[28]的通过学习不同任务间的关联关系有利于提升多个任务的建模效果这一结论,利用多任务学习的思路同时设计就业意图的可解释模块和就业单位推荐模块(见2.3节),其特点在于:2个任务共享特征嵌入层参数,即得到学生和单位特征嵌入后,分别对2个任务建模,如图1所示的点框内.
针对就业意图演化问题,借鉴自我感知理论研究成果[29-30](一个人的目标和内在动机可以通过人的行为来推断,而人们的行为反映出的日常生活规律被证明与工作或学业成绩有强烈的相关性),利用学生的学业成绩来辅助就业意图建模,提出门控循环单元(gated recurrent unit, GRU)网络[31]的就业意图演化过程学习方法,计算为
Gt=GRU(Gt-1,xt),t=1,2,…,6,
(3)
其中,Gt为第t个学期学生成绩的隐藏状态,xt∈d为第t个学期学生成绩的嵌入向量.将最后一个学期学生成绩的隐藏状态G6作为学生就业意图的演化结果,与学生和单位特征嵌入向量拼接,得到用于表征学生就业意图的嵌入向量,计算公式为
E=concat([P1,P2,…,PM,G6]).
(4)
Pm∈M×d为学生侧特征嵌入向量.最后,使用多层感知机(multilayer perceptron, MLP)[32]对就业意图进行建模,计算为
Op=Softmax(MLP(E)).
(5)
2.2.2 基于就业特征的解释模块
该模块包含2个注意力机制:抽取学生就业偏好的注意力机制和抽取单位能力要求的注意力机制.
1)抽取学生就业偏好的注意力机制有3个步骤:
① 在给定一对学生和就业单位信息的条件下,通过嵌入层得到学生侧特征的嵌入向量Pm∈M×d和就业单位侧特征的嵌入向量Qn∈N×d,其中M和N分别为学生侧和就业单位侧特征数量,m为学生特征的第m个,n为就业单位特征的第n个,d为嵌入向量维度.通过加和池化操作,将学生侧特征嵌入向量Pm聚合,得到学生表征向量Ps为
(6)
② 将学生表征向量Ps作为计算注意力权重的查询向量[33],用来计算学生对就业单位不同特征的偏好程度,结构如图2(a)所示,计算方法为
(7)
计算得到的注意力权重wn即表示了学生对就业单位第n个特征的偏好程度.

Fig.2 The structure of attention mechanism for extracting interests and requirements
③ 利用注意力权重对单位特征嵌入向量进行加权求和,得到学生就业偏好嵌入向量P具体计算方法为
(8)
2)抽取单位能力要求的注意力机制有3个步骤:
① 获得学生侧特征的嵌入向量Pm∈M×d和就业单位侧特征的嵌入向量Qn∈N×d.通过加和池化操作,将就业单位侧特征嵌入向量Qn聚合,得到就业单位表征向量Qu为
(9)
② 将就业单位表征向量Qu作为计算注意力权重的查询向量,用来计算就业单位对学生不同特征的偏好程度,结构如图2(b)所示,计算方法为
(10)
其中,计算得到的注意力权重wm即表示了就业单位对学生第m个特征的偏好程度.
③ 利用注意力权重对学生特征嵌入向量进行加权求和,得到单位能力要求嵌入向量Q具体计算方法为
(11)
该机制不仅使用可排序的就业单位特征重要性向学生解释了其就业偏好,还使用可排序的学生特征重要性解释了就业单位的能力要求.具体地,依据式(7)与式(10)将互惠性约束中对学生就业偏好和单位能力要求注意力机制输出的注意力分数(可排序的重要性评分)作为特征层级的解释.由式(7)计算出的已经归一化的注意力权重wn∈(0,1)表示学生对该就业单位第n个特征的注意力分数,即为学生的就业偏好解释.由式(10)计算出的已经归一化的注意力权重wm∈(0,1)表示该就业单位对学生第m个特征的注意力分数,即为单位的能力要求解释.
2.3 基于互惠性约束的就业推荐模块
互惠性约束的就业单位推荐需要同时满足学生就业偏好和单位能力要求.本模块采用模糊门机制[34]自适应聚合对学生就业偏好和单位能力要求的表征向量,输入到一个多层感知机,最终输出推荐结果,如图1虚线框所示.该模块的核心是基于模糊门机制聚合就业偏好与能力要求特征,即使用神经网络自适应动态地计算聚合权重,其计算方法为
R=wP+(1-w)Q,
(12)
其中,自适应权重w由一个二元神经网络实现,计算为
w=σ(WpP+WqQ).
(13)
其中,Wp和Wq分别为神经网络的参数矩阵.
3 实验与结果
3.1 数据集
本文实验所用数据集EMDAU的统计信息如表1所示,其中用户数为5届毕业生的总和,就业单位是5届学生就业单位的总和,交互记录为学生与就业单位的信息对(表达学生到就业单位的就业关系).该数据集中,学生特征含10个离散特征和6个连续特征,如表2所示;就业单位特征含6个离散特征,如表2所示.数据集中的就业意图由专家总结为出国留学、国内升学、签约就业3种,分布如图3所示.

Table 1 Statistical Information of EMDAU

Table 2 Feature Information of EMDAU
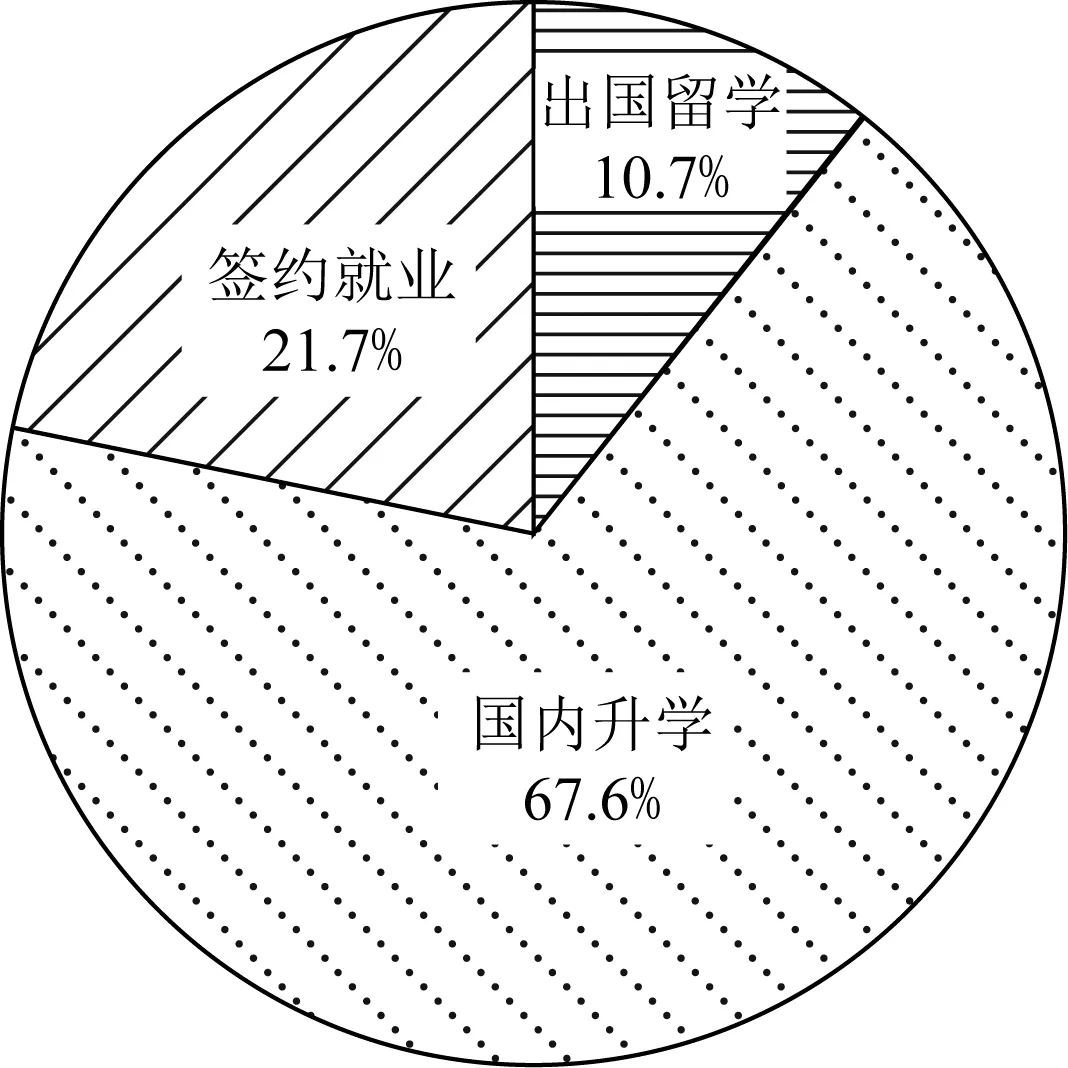
Fig.3 The distribution of employment intention in dataset
本文根据学生的毕业年份,将数量较小的两届毕业生数据分别作为验证集758条和测试集2 018条,将其余3届的毕业生数据作为训练集5 594条.
3.2 评价指标
在推荐研究领域,曲线下面积(area under curve,AUC)是一个被广泛应用的评价指标[35].AUC是衡量二分类模型性能的指标,其测量的是测试集中正样本排序在负样本前面的概率,反映了模型的排序能力.本文采用AUC这一评价指标来衡量就业推荐性能,其计算方法为
(14)
其中,ypos和yneg分别为模型对正样本和负样本的预测值,Npos和Nneg分别表示测试集中正样本和负样本的数量.
此外,本文参考文献[36],引入相对增益(relative improvement,RelaImpr)来衡量本文所提出方法与其他方法的增益.对于一个随机高斯分类器,AUC=0.5,因此RelaImpr的定义为
(15)
由于就业意图预测是一个多分类的任务,因此本文选用宏观F1(Macro-F1)和微观F1(Micro-F1)来衡量模型性能,计算方法为
(16)
(17)
式(16)中,N为类别数,F1-scorei为第i个类别的F1分数.式(17)中,Recall和Precision为所有类别总的召回率和精确率.
本文参考文献[37],使用多任务收益(MTL-Gain)指标衡量多任务学习相较于单任务学习的收益,其计算为
MTL-Gain=MMTL-Msingle,
(18)
其中,MMTL和Msingle分别为使用多任务学习和使用单任务学习的模型指标.
3.3 对照方法
本文将所提出方法与7个方法进行对比:
1)LR.Logistic回归方法在深度神经网络应用于推荐领域之前,被广泛使用.本文将其作为最基本的对照算法.
2)FM[38].因子分解机(factorization machines, FM)是经典的特征交叉方法,现在被广泛应用于各类推荐场景当中.
3)DeepFM[39].该方法是将FM算法和DNN结构结合的一种方式,①DNN用于抽取特征间的高阶交叉信息;②FM用于抽取特征间低阶交叉信息.
4)DeepCross[40].该方法利用带有残差连接的深度全连接神经网络以显式的方式学习非线特征交叉信息.
5)AutoInt[4].该方法利用多头自注意力机制代替专家知识,自动挑选有价值的特征组合进行特征交叉.
6)EXPLORE[41].EXPLORE是一个基于矩阵分解的方法,其利用主题建模算法学习标签的语义信息,推荐带有标签解释的物品.由于本文采用的数据集中一个用户仅有一条交互记录,无法直接使用矩阵分解.因此本文在实验中将学生特征和单位特征作为矩阵分解的表征向量.
7)AFN[42].该方法利用对数转换层将每个特征的幂转换为待学习的参数,实现自适应调整特征组合的阶数.
3.4 实验结果及分析
3.4.1 整体性能及分析
表3展示了在数据集EMDAU上各方法5次实验结果的平均.该实验结果表明,本文所提出的就业推荐方法性能优于所选对比方法;基于深度神经网络的方法效果均超过了LR;与文献[42]结果不一致的是:本实验中DeepCross的效果差于DeepFM,本课题组分析认为其主因是数据集EMDAU特征分布复杂性不高,且FM的低阶显式特征交叉[38](feature interaction)效果优于CrossNet的相对高阶显式特征交叉效果;本文所提方法优于AutoInt与AFN两个方法的主因是,后两者无法显式地聚合学生就业兴趣与单位能力要求;所提方法优于EXPOLRE的主因是,后者缺乏特征间的交互.
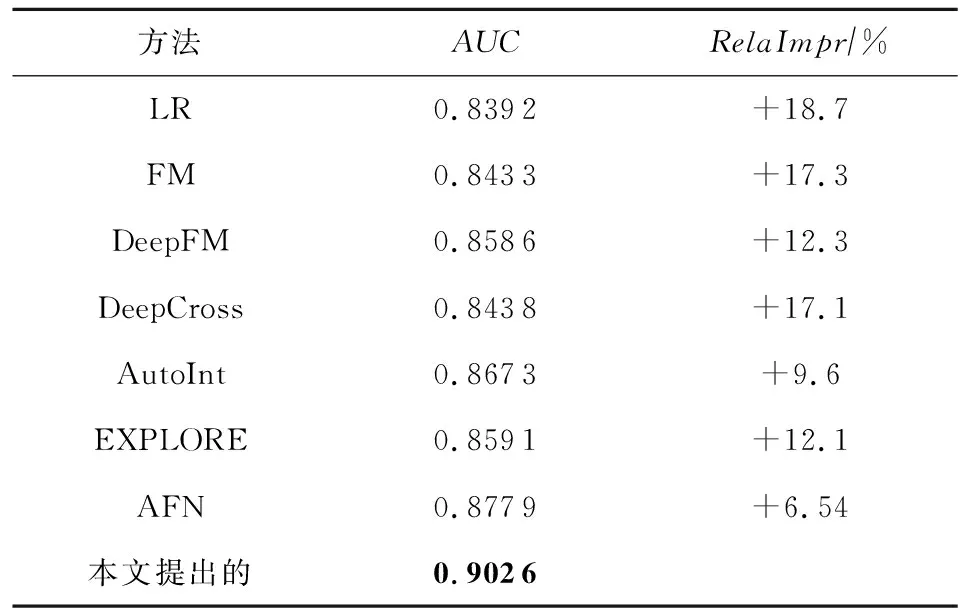
Table 3 The Recommendation Performance of Various Methods
3.4.2 互惠性约束的消融实验结果及分析
为了验证本文所提互惠性约束的有效性,课题组完成了4个消融实验:1)去除来自抽取学生就业偏好的注意力机制的输入;2)去除来自抽取单位能力要求的注意力机制的输入;3)去除模糊门聚合函数;4)保持所提方法不变.
如表4所示,该实验结果表明所提方法的推荐性能优于实验1)~3)方法,说明了本文所提出的互惠性约束3个成分对于就业推荐方法有增益作用.

Table 4 The Results of Ablation Experiment for Reciprocal-constrained Module
本文还同直接拼接(none)、平均池化(mean)、点积(dot)以及调和平均(harmonic)[43]等不同聚合方法进行了对比实验,实验结果表明:使用模糊门聚合函数的推荐效果最好,如表5所示,验证了模糊门聚合方法的有效性.
3.4.3 可解释模块对推荐任务性能影响分析
鉴于基于就业特征的解释模块未改变就业推荐模块的结构,对推荐性能没有影响,故本节分别对就业意图建模的单模型IntentPre、就业推荐建模的单模型UnitRec和本文所提出的多任务方法Ours进行对比实验,以验证基于就业意图的解释模块对推荐任务性能影响.如表6所示,实验结果表明所提多任务方法对于就业推荐任务和就业意图预测任务均有增益作用.
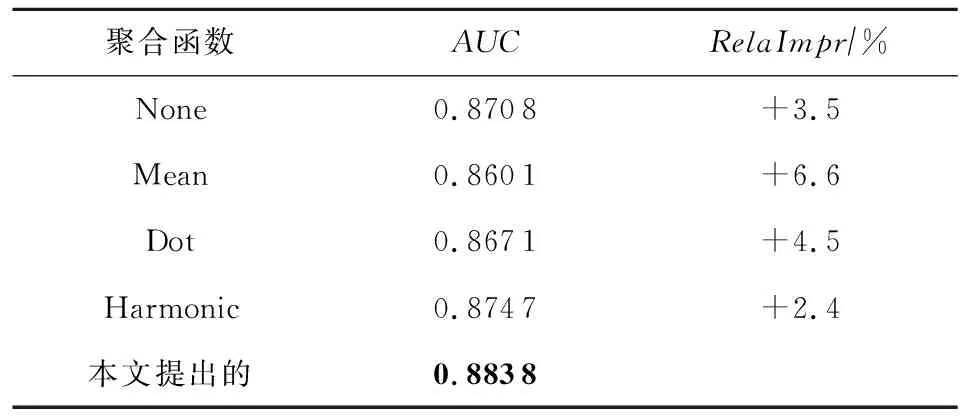
Table 5 The Comparison of Performance Between Different Aggregation Functions

Table 6 The Experimental Results of Interpretation Module
3.4.4 不同负采样方法对比和参数实验分析
为了验证基于相似度的随机负采样模块的有效性,本节完成2个实验.
1)5个不同负采样方法的对比实验.为了排除互惠性约束的干扰,在实验中,使用特征拼接的方式代替了互惠性约束.5个负采样方法分别为:①随机负采样方法Random;②基于相似度排序的负样本生成方法Similarc,即直接选择最不相似的N个单位(N为负样本个数)为负样本;③基于学生间相似度的随机负采样方法Similars,即使用学生间相似度得到高置信度负样本集,在该集合上随机负采样;④基于单位间相似度的随机负采样方法Similaru,即使用单位间相似度得到高置信度的负样本集合,在该集合上随机负采样;⑤本文所提的随机负采样方法Ours.如表7所示,实验结果表明基于相似度的随机负采样方法(Similars,Similaru,Ours)均优于随机负采样方法(Random),证明了本文所提出的基于相似度的负采样方法的有效性;基于相似度排序的负样本生成方法Similarc相比于其他方法性能下降明显,分析认为是由于该策略过分拉大了正负样本间的距离导致方法难以收敛,且该方法很大程度上改变了原始的数据分布;基于学生间相似度的随机负采样方法Similars和基于单位间相似度的随机负采样方法Similaru均略差于融合两者相似度的随机负采样方法,说明所提方法结合单位间相似度和学生间相似度完成随机负采样,得到的负样本置信度更高.

Table 7 The Experimental Results of Various Negative Sampling Methods
2)阈值参数实验.负样本选择阈值是按照相似度降序排序的负样本全集中选择出的负样本比例.该实验分别采用Similars,Similaru,Ours这3种随机负采样方法,以前10%,30%,50%,80%和100%的阈值选择,形成3组(每组5个)高置信度负样本集,训练出相应推荐模型,并在同一测试集上测试其性能.如图4所示,实验结果表明:3种随机负采样方法分别在30%,50%,80%的阈值上取得组内最佳效果.

Fig.4 The results of different dissimilar sets for random negative sampling
3.5 基于用户调研的推荐结果可解释性评估
借鉴文献[42]中的随机生成解释性评估方法,本文通过用户满意度调研,对比并统计分析所提方法生成的和随机生成的推荐解释效果.
3.5.1 实验设置
实验目的在于评估所提方法的解释性,而非其准确性,因此本文假设学生实际就业单位即为方法所推荐的单位,即保留学生实际就业单位在推荐列表Top10以内的样本.依此规则,从测试集中随机选择50名学生作为实验对象.针对每个学生,分别用所提方法生成推荐解释和随机生成推荐解释.其中推荐解释信息包含2个模块输出:基于就业意图的解释模块输出学生每一类就业意图的概率作为解释,以饼状图形式呈现,如图5(a)所示;基于就业特征的解释模块分别输出重要性评分前三的学生特征和重要性评分前三的就业单位特征作为解释,以柱状图形式呈现,如图5(b)和图5(c)所示.
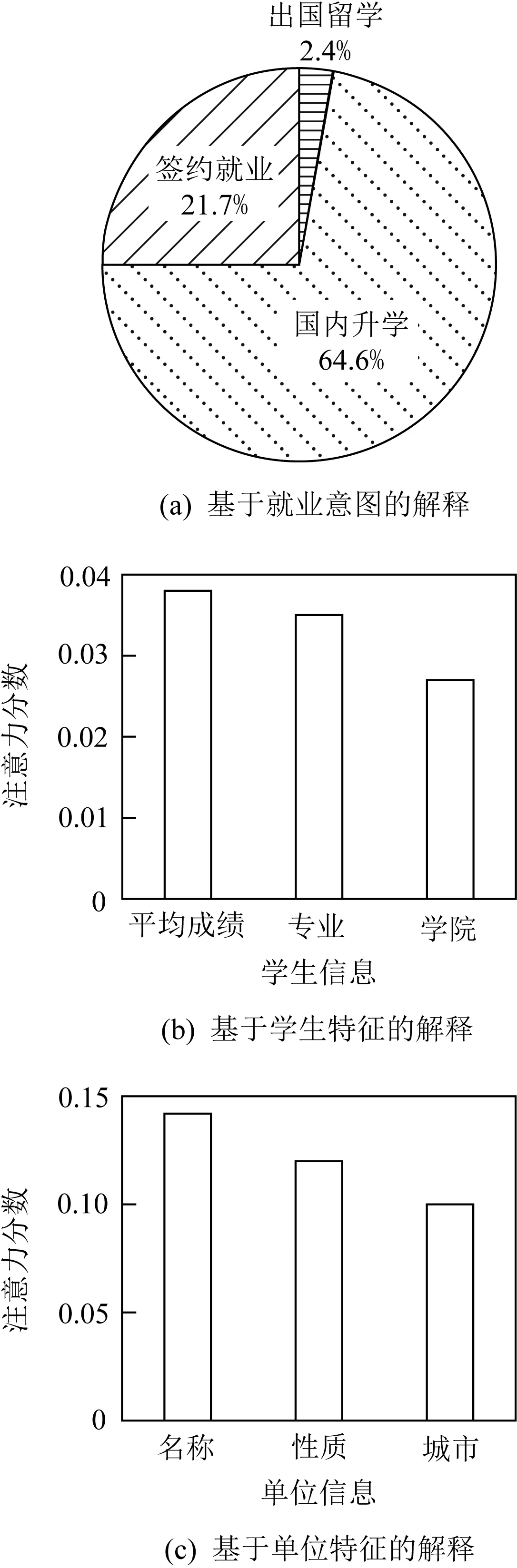
Fig.5 Illustration of interpretable recommendation information for a student
本实验依据随机双盲原则设计问卷,调研用户满意度来评估所提方法生成推荐解释的有效性.问卷中,给出所提方法生成的解释信息和随机生成的解释信息,并在问卷中随机编排为“解释1”和“解释2”;同时对每一个解释信息的满意度进行设问如表8中问题1~6.满意度设问基于李克特量表衡量用户满意度(即1~5分5个选项分别代表了“非常不同意”“不同意”“不一定”“同意”“非常同意”).问题7调研用户是否认为所提方法输出的解释信息更加合理,验证解释信息的有效性.
由于数据集EMDAU中实例已脱敏处理,无法对实验所选学生直接进行调研.为了保证调研对象的专业性和公平性,本实验从数据来源学校中邀请10名在学生就业辅导方面有丰富经验的教师作为问卷对象.在问卷调查中,考虑到不同教师在就业辅导经验上具有差异性,将10位教师随机分为2组,2组教师分别对实验所选的50位学生进行评价,每位教师回答10份学生问卷,最后共收回100份学生问卷.

Table 8 The Content of Questionnaire
3.5.2 实验结果分析
如表9所示,问题7的统计结果表明:认为所提方法生成解释性合理的问卷数量超随机生成方法的近1倍,证明了所提方法生成解释信息的有效性.

Table 9 The Statistical Results of Interpretation Rationality
图6以堆积图的形式展示了问题1~6满意度分数的统计结果,其中Mi,Ms,Mu分别表示所提方法生成的就业意图解释、学生特征解释以及就业单位特征解释,Ri,Rs,Ru分别表示随机生成的就业意图解释、学生特征解释以及就业单位特征解释.图6表明:从用户满意度角度观察,所提方法生成的就业意图解释和学生特征解释优于随机生成的解释;所提方法生成的就业单位特征解释略好于随机生成的解释,即所提方法的解释性较好.

Fig.6 The statistical results of question 1~6
从统计显著性角度来分析用户满意度,其结果如表10所示.可以看出:对于就业意图解释和学生特征解释,所提方法生成解释的满意度平均分高于随机生成解释,且配对t检验的p-value远小于0.05,这说明所提方法在统计意义上是显著有效的;对于单位特征解释,所提方法生成解释与随机生成解释的满意度平均分相近,且配对t检验的p-value远超0.05,这说明所提方法生成的单位特征解释有效性低.课题组分析认为后者的可能原因是数据集EMDAU中单位特征的数量较少且特征之间语义区分度[44]较小.

Table 10 The Average Scores and t-test Results of Question 1-6
4 总结与展望
本文提出了基于互惠性约束的可解释就业推荐方法.其特色在于综合运用多任务学习、注意力机制、门控网络,引入互惠性约束缓解了“能力失配”问题,构建兼顾就业特征和就业意图演化过程的可解释模块增强可解释性,设计基于相似度的随机负采样方法缓解了负样本不置信的问题.在真实数据集EMDAU上开展对比和消融实验,实验结果验证了所提出方法的性能优且有效.
未来,进一步扩展就业数据的特征集,深入地研究和分析就业特征之间的因果关系,使得就业推荐的解释具有因果性,破解潜在的可解释性失效问题.
作者贡献声明:朱海萍、田锋、陈妍3位作者提出研究思路,设计研究方案;赵成成作者负责设计和实施实验;田锋、刘启东作者负责论文起草和最终版本的修订,辅助实验;曾疆维作者负责数据采集、清洗和分析数据、实施实验;郑庆华、陈妍作者负责行政、技术和材料支持.

