混合驱动水下滑翔机用可折叠螺旋桨的设计
□ 毕 杰 □ 付 平 □ 张明赛 □ 殷 硕 □ 栾光旭 □ 王晨旭
青岛科技大学 机电工程学院 山东青岛 266061
1 设计背景
进入21世纪以来,世界各国普遍认识到海洋探测与开发对增强国家综合实力和促进科技创新的重要意义[1-2]。混合驱动水下滑翔机作为一种新兴的海洋探测平台,在海洋探测中发挥了不可替代的作用[3]。在传统混合驱动水下滑翔机实际应用中,存在一些问题,如仅依靠浮力驱动时,螺旋桨桨叶会产生一定的阻力。对此,笔者设计了新型可折叠螺旋桨用于混合驱动水下滑翔机,可以减小传统水下滑翔机的阻力,提高航行时的稳定性。
2 可折叠螺旋桨结构
混合驱动水下滑翔机用可折叠螺旋桨安装在机体尾部,螺旋桨工作时可以为水下滑翔机提供推力,螺旋桨不工作时可以减小水下滑翔机滑翔的阻力。目前,水面帆船与航空领域对可折叠螺旋桨有少量应用,但结构设计都相对复杂,不适合应用于水下滑翔机[4-5]。在水下滑翔机仅靠浮力驱动的滑翔过程中,航行速度较低,在螺旋桨两侧产生的压力不足以使螺旋桨自动折叠,因此需要设置一个使螺旋桨折叠的复位机构。考虑到水下滑翔机的成本与续航能力,所设置的复位机构结构应尽量简单,且不消耗水下滑翔机所携带的能量。笔者设计的混合驱动水下滑翔机用可折叠螺旋桨可借助启动时旋转的离心力张开,通过内部设置的复位机构,同时借助航行产生的压力实现折叠。
通过查阅其它领域可折叠螺旋桨的相关资料可知,在可折叠螺旋桨的直径与展开面积大小相等时,螺旋桨的效率与桨叶数成反比关系[6-7]。另一方面,较少的桨叶数量可以避免水下滑翔机在航行过程中产生空泡[8-9]。笔者以图谱设计法为基础,结合水下滑翔机的水动力参数,设计了新型可折叠螺旋桨,用于混合驱动水下滑翔机[10-11]。可折叠螺旋桨如图1所示,桨叶数为2,设计简单,安装便利。设计的难点在于复位机构的弹簧选型,弹簧弹性系数过大,桨叶不易展开,太小则折叠困难。
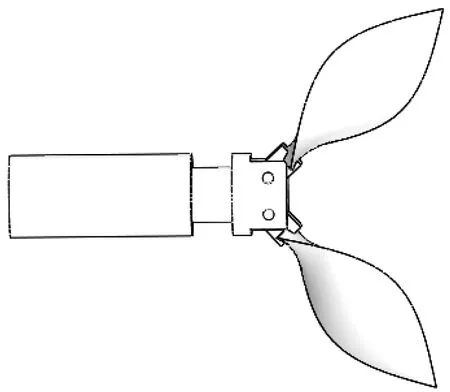
▲图1 可折叠螺旋桨
3 力学分析
新型可折叠螺旋桨展开时,依靠螺旋桨旋转时产生的离心力,不消耗其它能量,并在弹簧弹力、自身重力等力的共同作用下达到动平衡状态,稳定旋转。分析力平衡过程,需要建立惯性坐标系,如图2所示。惯性坐标系以螺旋桨轴的圆心为原点,以螺旋桨轴线指向桨叶方向为X轴正方向,以平行于螺旋桨轴径向截面指向桨毂右侧为Y轴正方向,以平行于螺旋桨轴径向截面指向桨叶外侧为Z轴正方向。图2中,C(xC,yC,zC)为桨叶质心坐标,位置矢量记为RC,m为桨叶的质量,r0为桨叶轴线与X轴的垂直距离,θ为桨叶的展开角度,ε为Z轴与竖直方向的夹角,g为重力加速度,MC为作用在桨叶旋转轴上的离心力矩,是桨叶展开的动力矩,MH为水动力推力矩,也是桨叶展开的动力矩,MS为弹簧扭矩,是桨叶展开的阻力矩,MG为重力力矩。

▲图2 惯性坐标系
在惯性坐标系中,桨叶在离心力与水动力推力下展开,需要满足如下方程式:
-MC-MH+MS+MG<0
(1)
动阻性与桨叶展开角度有关。
MC=∮mω2xi(zi+r0)dm
(2)
式中:ω为螺旋桨旋转角速度;dm为桨叶上的微元质量,坐标为(xi,yi,zi)。
将螺旋桨的转动视为刚体运动,通过三角函数变换,可将式(2)进一步转化为:
MC=mω2‖RC‖[‖RC‖sin(2θ)/2+r0cosθ]
(3)
(4)
式中:ρ为海水密度;n为螺旋桨转速;J为相关因数;KMH为水动力因数;Dp为螺旋桨直径。
MG=mgxCcosε
(5)
分析式(5)可知,夹角ε的大小决定MG的正负。当夹角ε的绝对值小于90°时,MG大于0,相当于阻力。当夹角ε的绝对值大于90°但小于180°时,MG小于0,相当于动力。
(6)
式中:ES为弹性模量;dS1为弹簧线径;dS2为弹簧中径;NS为弹簧圈数;θo为复位弹簧预装角。
在上述坐标系中,桨叶在弹簧弹力与水流压力作用下折叠,需要满足如下方程式:
MD+MS1+MG>0
(7)
MD为水下滑翔机航行时水流对桨叶背侧产生的水动力矩,是桨叶折叠的动力矩。MS1为弹簧扭矩,大小与桨叶展开过程相同,为桨叶展开提供动力矩。动阻性与桨叶展开过程相反。
MD=f(n,Dp,V,θ)
(8)
式中:V为螺旋桨进速。
与桨叶展开过程相似,MG的正负由夹角ε的大小决定。当夹角ε的绝对值小于90°时,MG大于0,相当于桨叶折叠过程中的动力。当夹角ε的绝对值大于90°但小于180°时,MG小于0,相当于桨叶折叠过程中的阻力。
总结可折叠螺旋桨的展开与折叠过程,同时满足的条件为:
(9)
整理式(9),得:
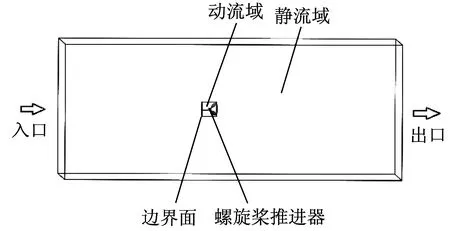
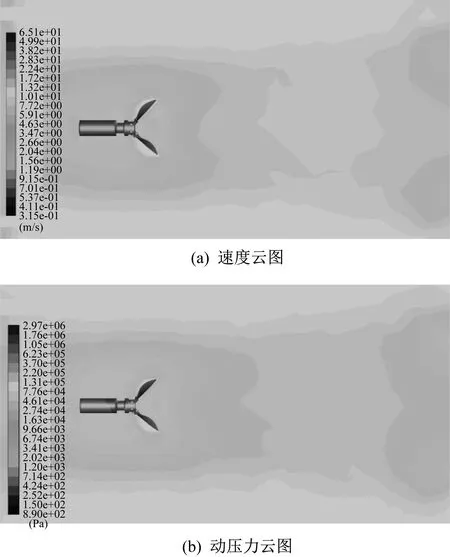
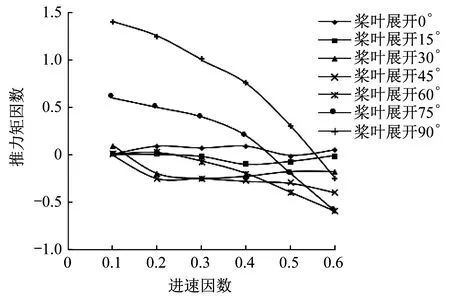
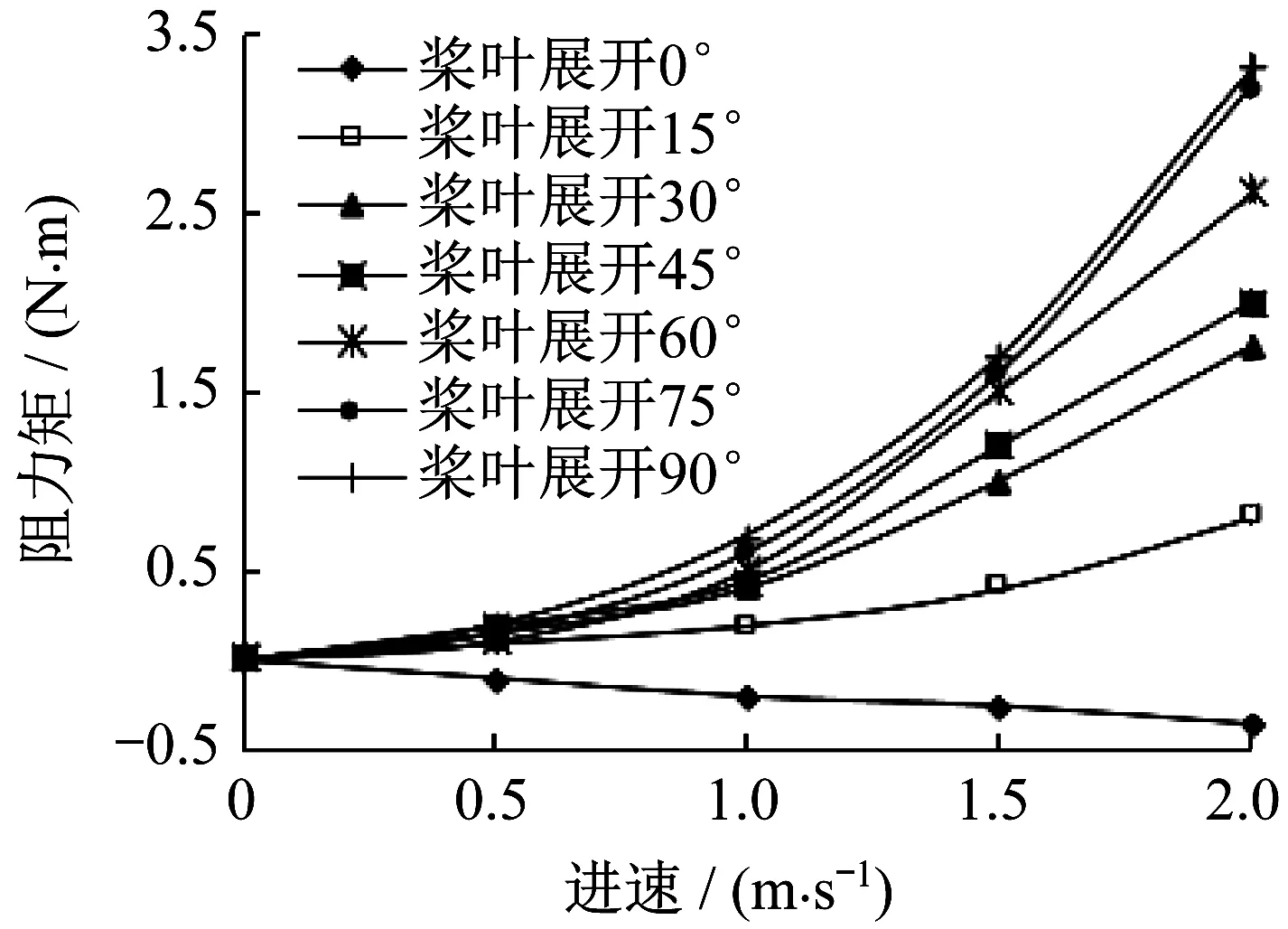
-MG-MD (10) 最终可得复位机构弹簧刚度因数KS需满足: (11) 式中:KMH为推力矩因数。 应用Fluent流体动力学软件,对所设计的混合驱动水下滑翔机用可折叠螺旋桨设置合理的仿真域,如图3所示。 ▲图3 可折叠螺旋桨仿真域 选择k-ε湍流模型,计算残差设置为10-5。仿真域分为动流域与静流域。静流域为长方体,长为25倍螺旋桨直径,宽和高为10倍螺旋桨直径。动流域为圆柱体,底面直径与高为1.1倍螺旋桨直径。流域左端面设置为流入边界,流入速度为0.5~1.5 m/s,对应的进速因数为0.1~0.6。流域右端面设置为流出边界,四周设置为对称边界。螺旋桨实体壁面设置为非滑移壁面,转速设置为600 r/min。桨叶展开角为0°~90°,对桨叶每展开15°分析一次。桨叶展开45°与桨叶展开90°时,仿真分析云图分别如图4、图5所示。 由图4、图5可知,桨叶展开45°时,螺旋桨水动力性能要优于桨叶展开90°时。就螺旋桨结构而言,两者均未发生边界分离,也未产生旋涡中心,水动力性能较为理想。从速度云图看,桨叶展开45°与桨叶展开90°时的平均速度分别为4.53 m/s、2.69 m/s,说明桨叶折叠后减阻效果较好。从动压力云图看,桨叶展开45°相比桨叶展开90°,螺旋桨整体动压变化更为平稳,压力损失更小。 在螺旋桨的性能研究与设计中,需要对螺旋桨模型进行水动力性能测试,即敞水性能试验。敞水性能试验可以分析几何要素对螺旋桨性能的影响,从而预估螺旋桨的水动力性能。 对桨叶每展开15°分析一次,得到各展开角度下螺旋桨不同进速因数的推力矩。结合式(11),推力矩因数KMH为: (12) ▲图4 桨叶展开45°仿真分析云图 ▲图5 桨叶展开90°仿真分析云图 基于式(12)计算得到的数据,绘制不同桨叶展开角度时螺旋桨推力矩因数随进速因数变化曲线,如图6所示。 分析图6可知,在固定桨叶展开角下,螺旋桨的推力矩因数整体随进速因数的增大而减小。桨叶展开角小于30°时,推力矩因数的变化不明显,即桨叶展开角较小时,螺旋桨的推力矩因数基本不受进速因数影响。进速因数为0.1时,推力矩因数最大,此时螺旋桨只旋转不前进,推力矩达到最大,最有利于桨叶展开。桨叶展开角小于45°时,随着桨叶展开角的增大,螺旋桨推力矩因数减小,桨叶展开变得困难。桨叶展开角大于45°时,随着桨叶展开角的增大,螺旋桨推力矩因数增大,桨叶展开变得容易。这是因为桨叶展开角度越大,桨叶周围流场的影响越小。笔者在设计可折叠螺旋桨时,注意了桨叶最小推力矩下的最小折叠角,从而避免正常展开受到影响。 ▲图6 螺旋桨推力矩因数随进速因数变化曲线 除分析螺旋桨的水动力性能外,还需要分析折叠过程中阻力矩变化情况,从而分析螺旋桨在折叠过程中的平衡状态。与螺旋桨展开过程分析相似,对桨叶每折叠15°分析一次,得到不同进速时的阻力矩,绘制螺旋桨阻力矩随进速变化曲线,如图7所示。 ▲图7 螺旋桨阻力矩随进速变化曲线 分析图7可得,螺旋桨折叠过程中,螺旋桨阻力矩随桨叶展开角的减小而减小,这也说明在航行过程中,相较于传统螺旋桨,可折叠螺旋桨不工作时,可以大大减小所受阻力,并且进速越大,效果越明显。折叠到某一桨叶展开角前,螺旋桨阻力矩与进速成正相关。在螺旋桨完全折叠时,螺旋桨阻力矩随进速的增大而减小,说明在仅靠浮力驱动滑翔时,相比于传统螺旋桨,可折叠螺旋桨的低阻性更具有优势。 笔者针对混合驱动水下滑翔机仅在浮力驱动时螺旋桨会产生一定阻力的问题,设计了一种新型可折叠螺旋桨。对新型可折叠螺旋桨桨叶展开与折叠过程进行了力学分析,并确定了复位机构的数学模型。同时在不同桨叶展开角时,对新型可折叠螺旋桨进行了水动力性能分析。结果表明,相比传统螺旋桨,在螺旋桨不工作时,可折叠螺旋桨可以大大减小混合驱动水下滑翔机所受的阻力,并且进速越大,效果越明显。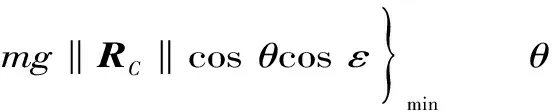
4 水动力性能分析

5 结束语

