基于电磁感应加热的硫化机热板温度场分析*

□ 孙国通 □ 陈 兴 □ 王 进 □ 孙宝寿

1.宁波大学 机械工程与力学学院 浙江宁波 315211 2.浙江省零件轧制成形技术研究重点实验室 浙江宁波 315211

1 研究背景

在用硫化机热板加工橡胶制品的过程中,热板表面温度不均匀容易造成橡胶制品发生硫化不完全情况,严重制约最终产品的成型,成为制造瓶颈。传统硫化机热板采用油加热或电阻加热[1],加热效率较低,且热板表面温度难以达到理想水平。电磁感应加热控制方式简单,在短时间内能产生大量热量,成为当今加热方式的研究热点之一[2-3]。电磁感应加热主要通过控制电磁感应过程中的电流、频率来达到控制加热的目的[4]。Eom等[5]研究发现,随着电磁波频率及电流的增大,硫化机热板的温差也增大。余露等[6]应用正交法对电磁参数进行优化,相对而言,电磁参数中电流的影响比较大,优化后热板温差为3 K。陈富豪等[7]结合遗传算法与神经网络,对感应频率、感应电流密度、时间进行优化,得到最的优参数组合。赵朋成等[8]运用模糊控制原理控制感应过程中的加热功率,改善热板温度的均匀性,同时确认由于电磁感应现象的复杂性,线圈的形状对加热所产生的影响也不容忽视。Huang Mingshyan等[9]提出使用分层式线圈,结合主成分分析及田口法来优化线圈的结构,可以将热板的温差控制在3 K以内。胡晓飞[10]研究得出,采用矩形线圈加热热板,温度较均匀,同时推导得到热板发热区域与线圈形状相关。Mrozek[11]发现磁屏蔽材料可以改善热板上磁通密度的分布,以达到优化的目的,但并未解决如何排布屏蔽材料。

以上研究通过线圈设计、参数优化、添加磁屏蔽材料来解决热板表面温度均匀性问题。笔者通过采用COMSOL商业仿真软件对电磁感应加热下的硫化机热板进行模拟仿真,分析喷涂不同尺寸及形状45号钢涂层时的加热效率,研究如何选择保温电流,并采用温度不均匀因数来评估热板最终的温差,为在电磁感应加热下的硫化机热板优化设计提供参考。

2 电磁感应加热理论

电磁感应加热源自法拉第发现的电磁现象,当线圈接通交流电时,在线圈周围会产生交变磁场。在交流磁场中,金属导体切割磁力线产生涡流,从而使导体内发热。

2.1 电磁场控制方程

由积分形式转换为微分形式的麦克斯韦方程组适用于所存在空间的任意一点,电磁感应加热时的电磁场控制方程为:

(1)

式中:A为磁矢量,Wb/m;为梯度算子;J为总电流密度矢量,A/m2;Je为涡流密度矢量,A/m2;Js为源电流密度矢量,A/m2;σ为电导率,S/m;μ1为磁导率,H/m;t为时间,s;Φ为标量势,V。

对式(1)取散度,得:

(2)

(3)

综上得到热板电磁场控制方程为:

(4)

对于热板及线圈周围空气域,假设Je、Js为0,则控制方程为:

(5)

对于线圈,假设涡流可以忽略,则控制方程为:

(6)

2.2 温度场控制方程

求解电磁场和涡流场的目的是利用电磁感应产生的焦耳热作为内部热源来计算温度场。温度场控制方程为:

(7)

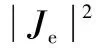
(8)

式中:ρ为材料密度,kg/m3;c(T)为比热容,J/(kg·K);λ(T)为导热系数,W/(m·K);qv为涡流引起的热源强度,W/m3;T为热板温度,℃。

2.3 温度场边界条件

线圈与空气交界面的边界条件方程为:

-nair·(-λairTair)-ncoil·(-λcoilTcoil)=0

(9)

式中:nair、ncoil分别为空气边界和线圈边界的法向向量;λair、λcoil分别为空气和线圈的导热系数;Tair、Tcoil分别为空气和线圈的温度梯度。

无穷域的边界条件为:

T=T0

(10)

式中:T0为初始温度,T0=25 ℃。

绝缘层的电荷量q为0。

热传导的边界条件为:

(11)

式中:T1、T2为热传导两侧的温度;λ1、λ2为热传导两侧的导热系数;n为热传导法向方向。

热板表面与空气域边界条件为:

=hw(Tα-T)+hm(Tα-T)

(12)

(13)

式中:nx、ny、nz依次为X、Y、Z方向向量;hm为热辐射系数,W/(m2·K);hw为对流换热系数,W/(m2·K);Tα为环境温度模型,取25 ℃;ε为辐射率模型,取0.68;σs为斯特藩-玻尔兹曼常数。

2.4 电磁场边界条件

模型域边界可以分为两类,一类是不同介质的界面,另一类是场的外边界。

不同介质的界面边界条件为:

(14)

式中:H1、H2为两侧磁场强度,A/m;B1、B2为两侧磁通密度,Wb/m2;n为单位法向量;t1为单位切向量。

场的外边界在不同条件下有不同的边界条件。通量平行边界条件为:

A=0

通量垂直边界条件为:

无限域边界条件为:

A=0

在感应加热的过程中,由于涡流的影响,在靠近线圈的热板底部薄层中首先产生热量,热量的穿透深度δ为:

(15)

式中:f为交流频率,Hz;ρ1为电阻率,Ω·m。

3 热板温度场分析

3.1 热板物理模型

热板电磁感应加热模型如图1所示,安装位置如图2所示。采用热喷涂工艺在热板上喷涂45号钢涂层[12],为研究喷涂形状对电磁加热的影响,喷涂方式一般选择菱形喷涂、全喷涂、三角形喷涂、仿线圈形状喷涂、圆形喷涂、正方形喷涂。

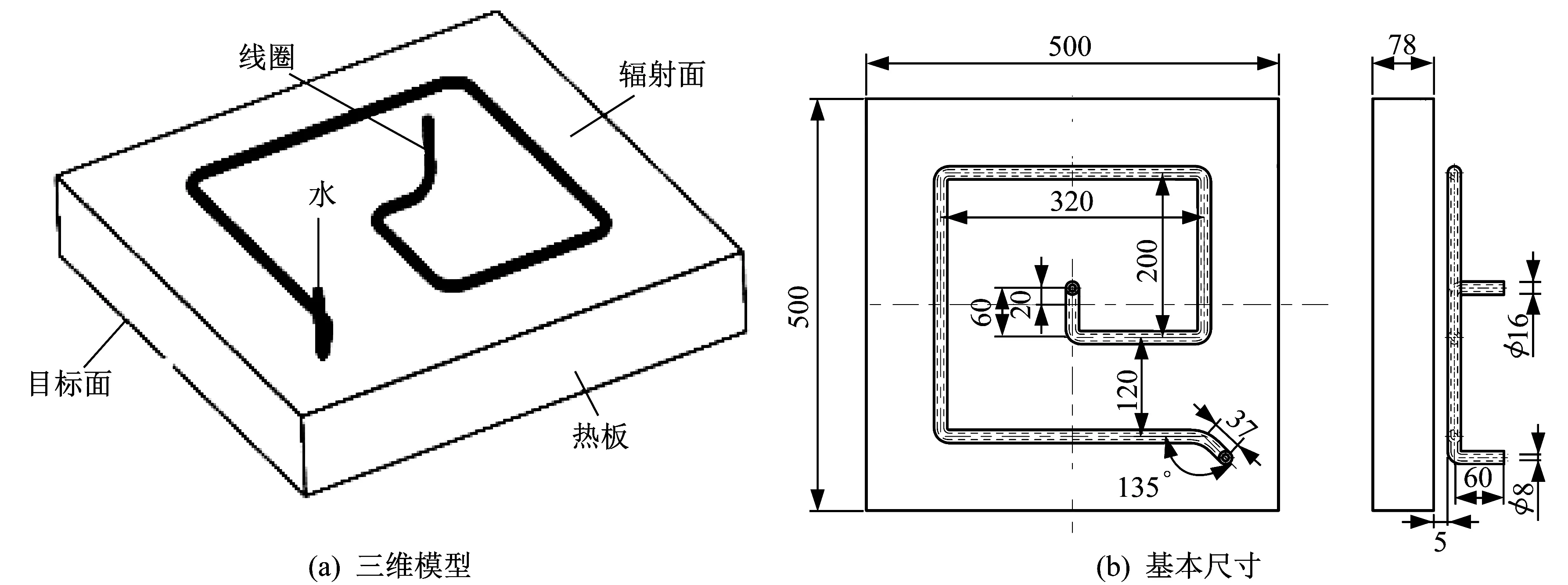
▲图1 热板电磁感应加热模型

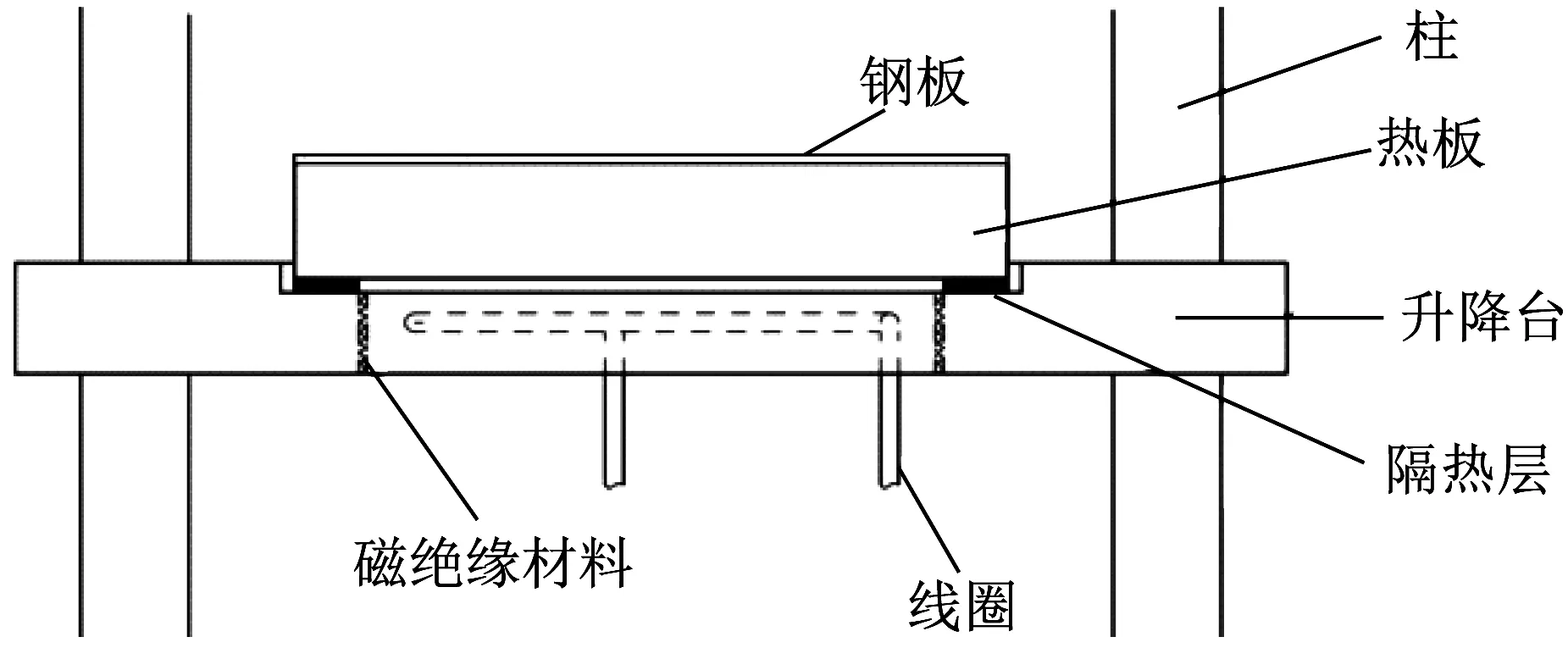
▲图2 热板安装布置

在SolidWorks软件中建立热板三维模型,并建立六种喷涂模型,如图3所示。

热板平面尺寸均为500 mm×500 mm,线圈直径为16 mm,冷却管道直径为8 mm,所使用的线圈与喷涂表面距离为5 mm。菱形喷涂尺寸为32 mm×32 mm,每个菱形喷涂间距为7 mm。全喷涂尺寸为320 mm×320 mm。三角形喷涂为等边三角形,边长为32 mm,每个三角形喷涂间距为7 mm。仿线圈形状喷涂尺寸为46 mm。圆形喷涂直径为32 mm,每个圆形喷涂间距为7 mm。正方形喷涂尺寸为32 mm×32 mm,每个正方形涂漆间距为7 mm。

根据式(15)可以得出,选用频率为70 kHz时,在感应加热过程中热量的穿透深度为0.08 mm。由于穿透深度和频率成反比,因此可选取较高的频率。喷涂厚度需大于穿透深度,由此选择喷涂厚度为0.3 mm。与文献[13]介绍的传统热板不同的是,笔者在紫铜热板顶面处额外增加2 mm厚的45号钢钢板,用于延缓温度的迅速下降。

3.2 模型材料参数

模型中线圈及热板材料为铜,涂层及热板底面材料为45号钢,所采用的材料属性见表1。热板温度通常不高于300 ℃,因此不会使45号钢涂层达到居里温度。

表1 模型材料属性

3.3 有限元模拟

根据以上分析,应用SolidWorks软件进行热板几何建模后,将六种喷涂类型模型以.step格式文件导出,并在COMSOL Multiphysics软件中依次导入文件,设置模型材料属性,进行模型网格划分,如图4所示。感应电流为850 A,仿真频率为50 kHz,线圈与热喷涂涂层间距为5 mm,环境温度为25 ℃,辐射率为0.68。

线圈在电磁感应加热过程中,由于趋肤感应的存在,线圈外表面是感应电流的主要分布区域,在划分网格时,需要对线圈的外表面进行集中网格细化处理。在COMSOL软件中采用扫略网格对线圈进行网格划分。硫化机热板的工作区域形状规整,此部分网格划分采用六面体网格扫略。对于与线圈接近的热板面,为保证仿真精度,需要进行额外细化处理。网格尺寸需小于热板的趋肤深度。对于模型中的空气域,由于区域形状复杂,可以采用四面体网格来划分。需要注意的是,因为线圈与热板附近的空气域接触为曲面物理场,为保证有较好的计算精度和收敛性,需要进行网格细化处理。

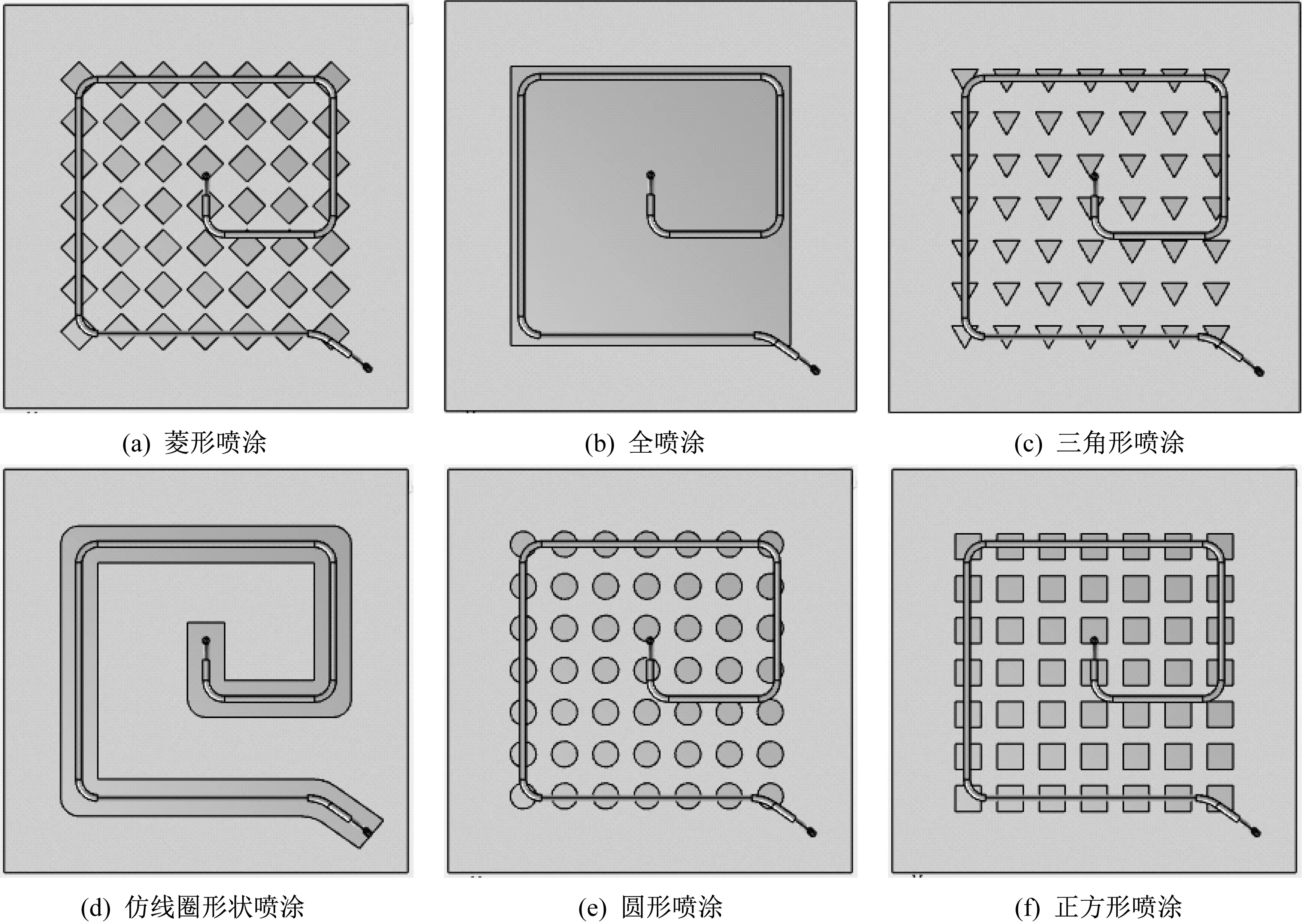
▲图3 热板喷涂模型

▲图4 模型网格划分

设置热板目标面温度为120 ℃,观察热板目标面温度分布云图及目标面温差情况,分析在达到相同温度120 ℃时六种喷涂方案温升的速率及温升过程中目标面温度的均匀性。若电流一直保持在850 A,则热板目标面温度会随加温时间的延长而持续升高。过高的温度会对硫化产品造成不利影响,如破坏硫化产品内部分子链破坏,硫化反原导致产品性能降低等。为使热板在达到所需温度时能够保持温度稳定,需要在目标面温度达到120 ℃时及时减小加热电流,进入保温阶段,并调整好保温电流。此时热板45号钢涂层最高温度会明显下降,并逐步趋于稳定,热板表面最小温度与最大温度的温差也会随着时间的延长而不断减小,热板的温度达到均匀。由于保温电流的影响相对独立,因此笔者分析在加热过程中如何合理确定保温电流。

3.4 目标面温度对保温电流影响

仿真中,保温电流和目标面温度关系如图5所示。

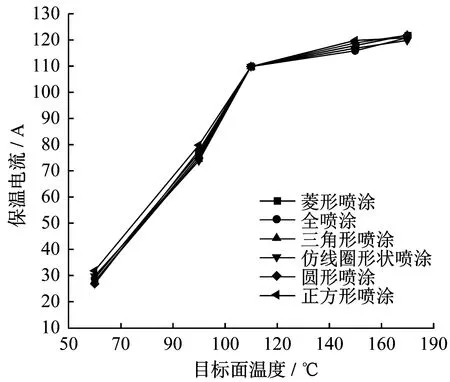
▲图5 保温电流与目标面温度关系

由图5可以发现,目标面温度升高时,所对应的保温电流增大。热板目标面温度升高时的热量方程为:

QT=QE-QL

(16)

式中:QT为温升时吸收的热量;QE为涡流发热量;QL为热损失。

目标面温度升高可分为两个阶段,第一是加热阶段,第二是保温阶段。第一阶段中,随着加热电流增大,涡流发热增加,温升速度加快,此时热板目标面最高、最低温度的温差也会增大。第二阶段中,随着保温时间的延长,目标面最高、最低温度的温差逐步减小,并趋近于零。当QT为零时,式(16)变为:

QE=QL

(17)

此时目标面达到热平衡,目标面温度处于稳定,保温电流仅起到维持热板目标面温度均匀的作用。如果目标面的目标温度高,那么所对应的保温电流需相应增大。由图5还可以发现,当目标面温度为60～120 ℃时,保温电流变化斜率较大,保温电流由30 A增大到110 A;当目标面温度为120～180 ℃时,保温电流变化斜率相对较小,保温电流逐渐稳定在120 A。

3.5 温度均匀性评估

引入温度不均匀因数公式对目标面温度均匀性进行评估,通过对热板加热后热板目标面的温度不均匀因数进行有效统计计算,量化热板目标面温度场分布的均匀性。目标面网格如图6所示。温度不均匀因数是目标面温度标准差与目标面平均温度的比值,反映的是热板目标面达到目标温度后热板表面温度的分布情况。通过加热过程中热板表面温度不均匀因数的变化趋势,可以评估热板表面温度均匀性。温度不均匀因数Kt为:

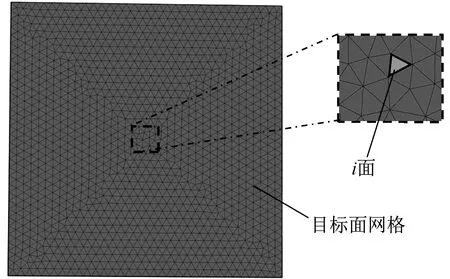
▲图6 目标面网格

(18)

温度不均匀因数越小,热板目标面温度的均匀性就越好。

3.6 温度场分析结果

六种不同喷涂方案在电磁感应加热3 000 s后热板目标面的温度分布云图如图7～图12所示,温度变化曲线如图13～图18所示。菱形喷涂方案在加热时间达到2 220 s时,热板目标面最高温度达到初始设定目标温度120 ℃。这一阶段在喷涂层中产生涡电流,目标面温度匀速上升。随着加热时间的延长,进入保温阶段。由于铜具有优良的导热能力,使热板目标面温度快速上升,并使目标面温度逐渐趋于均匀。进入保温阶段且加热时间达到3 000 s后,热板目标面最高温度为120.100 ℃,最低温度为119.648 ℃。全喷涂方案在加热时间达到1 120 s时,热板目标面最高温度达到初始设定目标温度120 ℃,然后调整加热电流,在加热时间达到3 000 s后,热板目标面最高温度为120.430 ℃,最低温度为120.231 ℃。三角形喷涂方案在加热时间达到1 410 s时,热板目标面最高温度达到初始设定目标温度120 ℃,在加热时间达到3 000 s后,热板目标面最高温度为122.878 ℃,最低温度为117.898 ℃。仿线圈形状喷涂方案在加热时间达到710 s时,热板目标面最高温度达到初始设定目标温度120 ℃,在加热时间达到3 000 s后,热板目标面最高温度为121.128 ℃,最低温度为120.950 ℃。圆形喷涂方案在加热时间达到2 800 s时,热板目标面最高温度达到初始设定目标温度120 ℃,在加热时间达到3 000 s后,热板目标面最高温度为119.627 ℃,最低温度为117.657 ℃。正方形喷涂方案在加热时间达到2 220 s时,热板目标面最高温度达到初始设定目标温度120 ℃,在加热时间达到3 000 s后,热板目标面最高温度为120.957 ℃,最低温度为120.658 ℃。

▲图7 菱形喷涂方案温度云图

▲图8 全喷涂方案温度云图

▲图9 三角形喷涂方案温度云图

▲图10 仿线圈形状喷涂方案温度云图

▲图11 圆形喷涂方案温度云图

▲图12 正方形喷涂方案温度云图

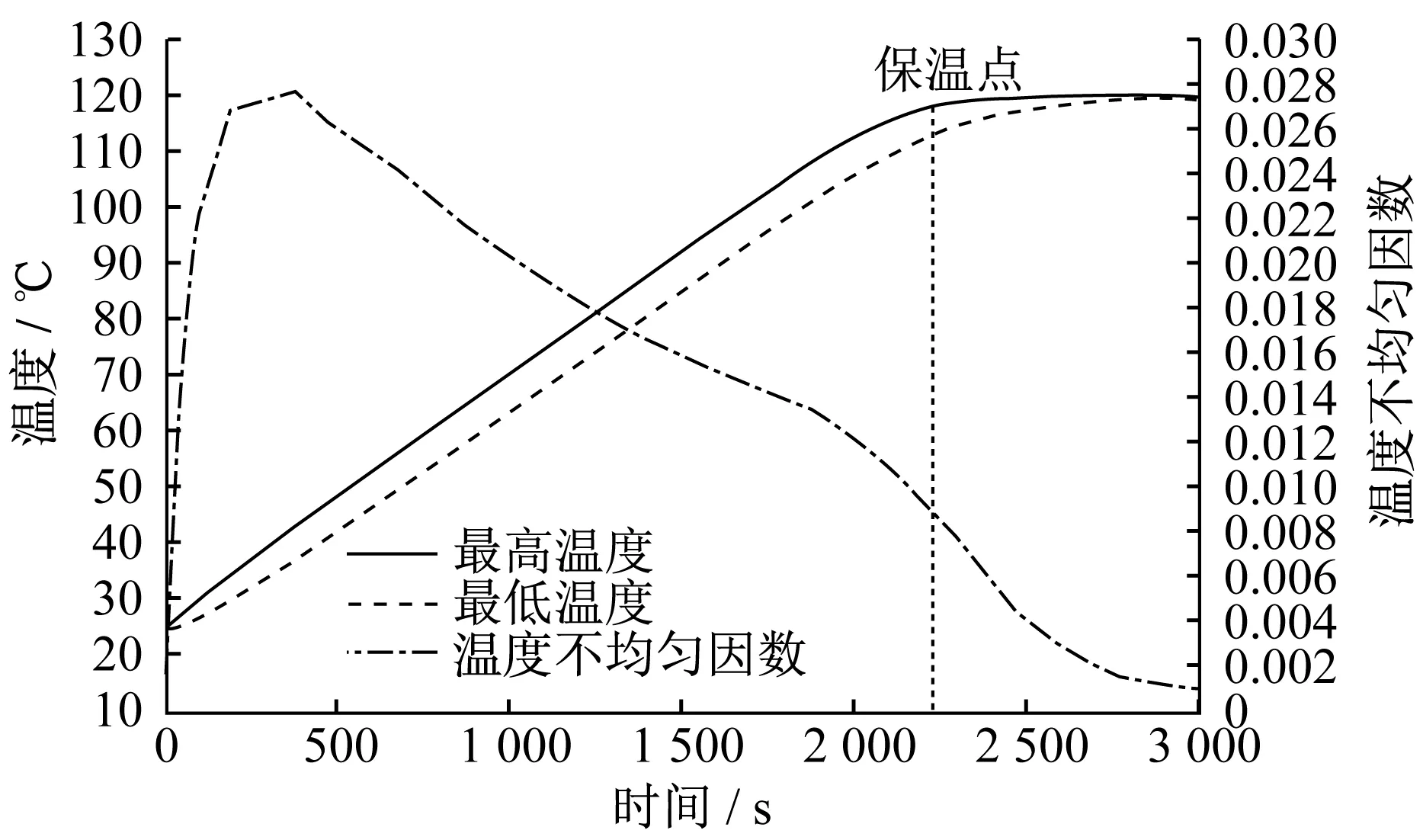
▲图13 菱形喷涂方案温度变化曲线

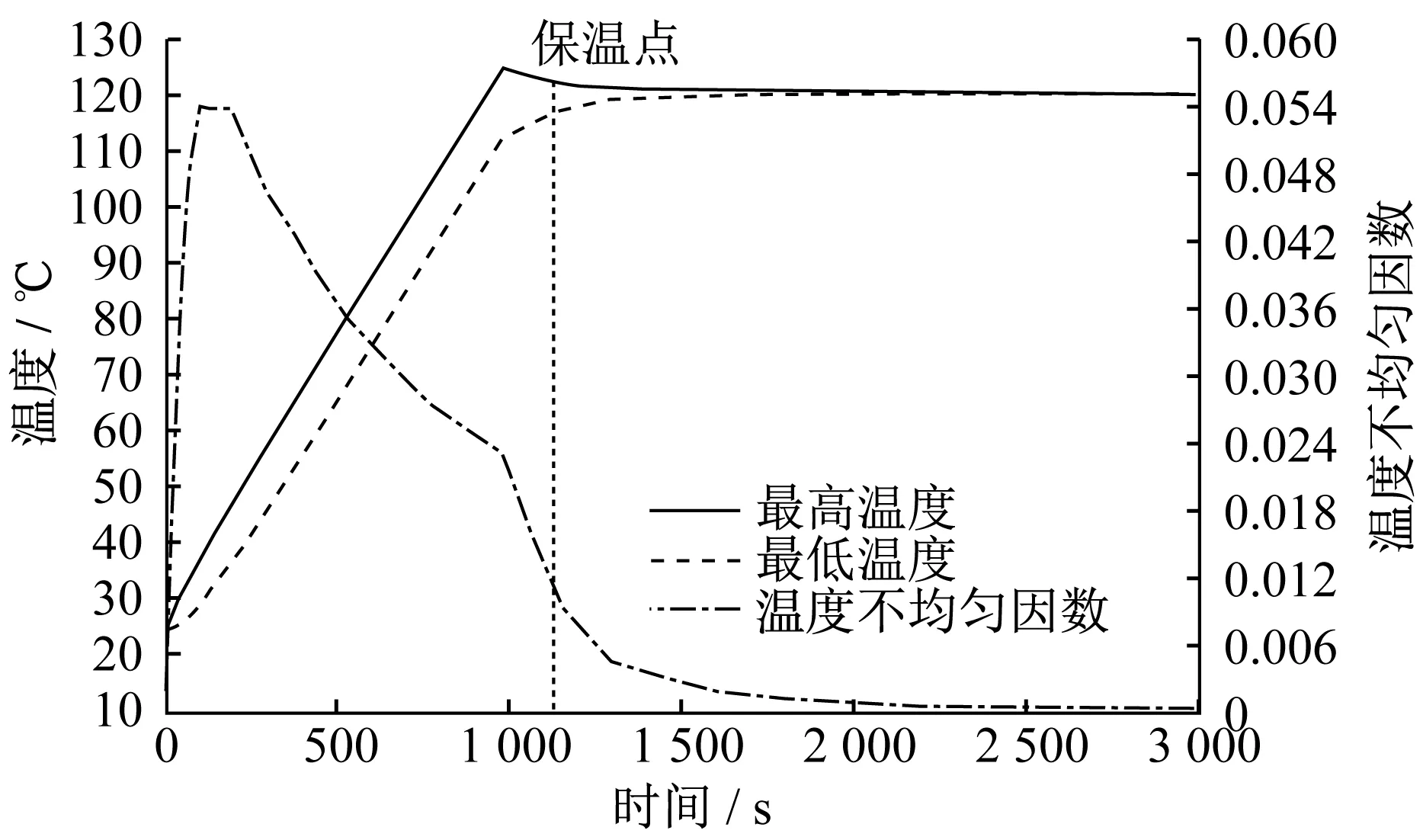
▲图14 全喷涂方案温度变化曲线

▲图15 三角形喷涂方案温度变化曲线

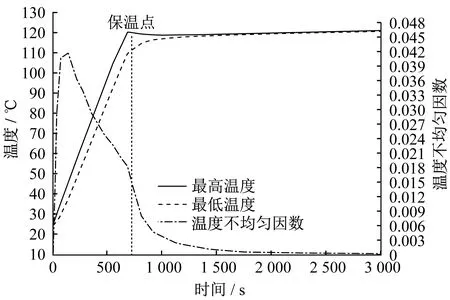
▲图16 仿线圈形状喷涂方案温度变化曲线

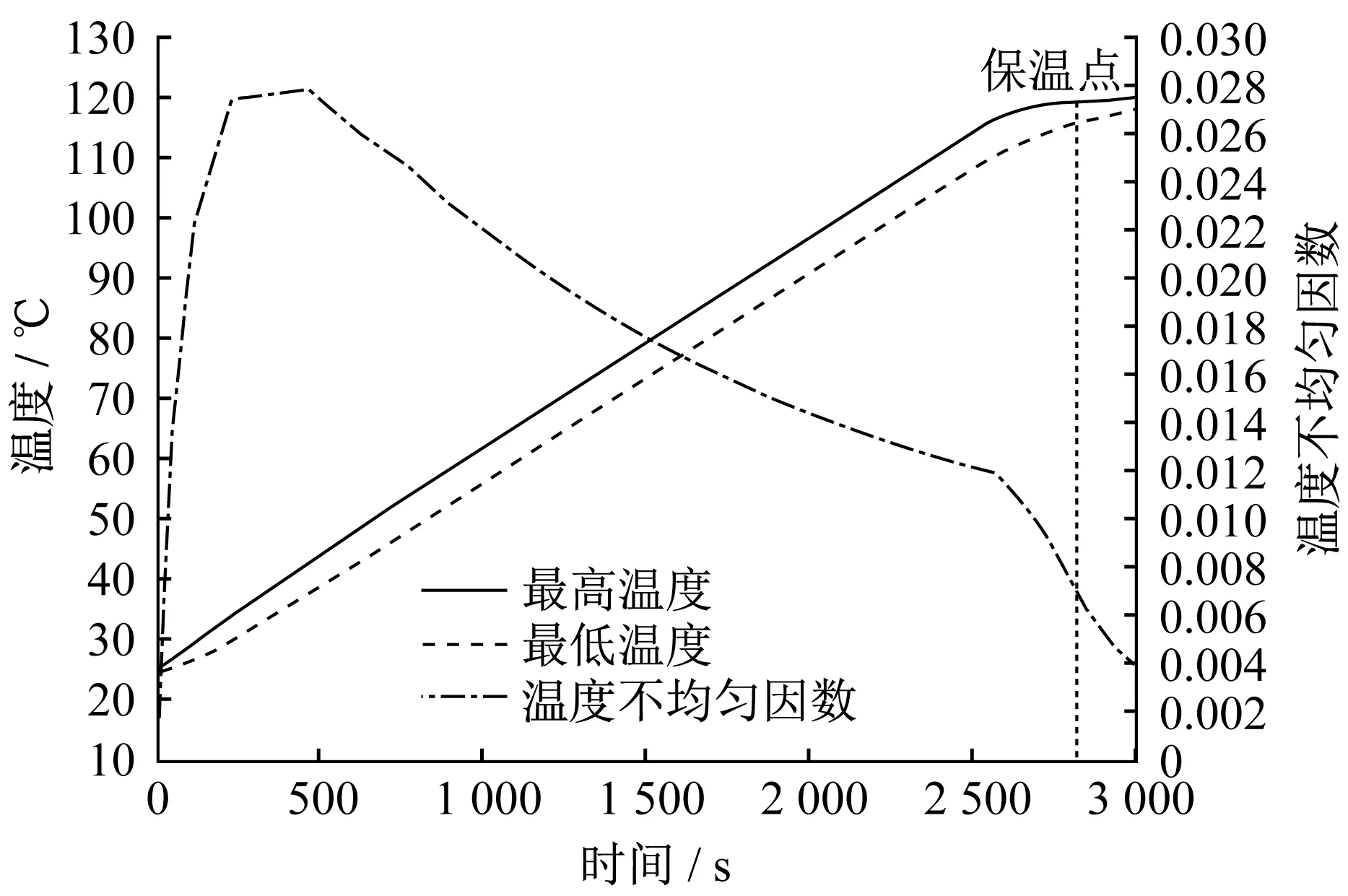
▲图17 圆形喷涂方案温度变化曲线

▲图18 正方形喷涂方案温度变化曲线

由分析可以发现,仿线圈形状喷涂方案最优,可以在较短时间内满足热板目标面的温差要求,温度不均匀因数小于0.001。全喷涂方案整体加热速率低于仿线圈形状喷涂方案,但优于其余四种喷涂方案。全喷涂方案在加热时间达到1 120 s的过程中,温差较大,接近12 K,在施加保温电流后,最终温差与仿线圈形状喷涂方案几乎一致,为0.2 K。当然,全喷涂方案经济成本较高。三角形喷涂方案加热速率良好,处于六种喷涂方案中间值,但加热过程中热板目标面温差过大,大于50 K,虽然可以采用保温电流方式来调节最终温差,但最终温差仍然接近5 K左右。菱形喷涂方案、圆形喷涂方案、正方形喷涂方案虽然在加热过程中可以将温差控制在5～7 K,但是在加热速率方面远低于其它三种喷涂方案,并且耗能大。

由加热过程中热板目标面温度不均匀因数的变化趋势可以看出,未达到目标温度120 ℃时,六种喷涂方案在加热初期温度不均匀因数呈线性增大趋势,并迅速达到峰值,其中,三角形喷涂方案在加热420 s后达到峰值0.136,菱形喷涂方案、正方形喷涂方案、圆形喷涂方案在加热370 s后依次达到峰值0.027、0.027、0.024,仿线圈形状喷涂方案在加热130 s后达到峰值0.042,全喷涂方案在加热100 s后达到峰值0.054。在六种喷涂方案温度变化曲线中,还有温度不均匀因数第二次下降的现象,这是因为施加保温电流后,热板目标面温度的均匀性得到迅速改善,三角形喷涂方案由未施加保温电流时的0.092下降到施加保温电流后的0.01,菱形喷涂方案、正方形喷涂方案由0.01下降到0.001,圆形喷涂方案由0.008下降到0.004,全喷涂方案、仿线圈形状喷涂方案分别由0.012、0.12下降到接近于0.000 1。综合评估六种喷涂方案目标面的温度不均匀因数,可以得到仿线圈形状喷涂方案为最优方案。

4 仿线圈形状喷涂方案参数优化

综合以上分析,选择仿线圈形状喷涂方案进行参数优化设计。通常影响热板表面温差的主要因素为加热频率、线圈与喷涂层距离、加热电流。正交试验能够从全面试验中选取具有代表性的试验组合,使试验具有均匀分散、齐整可比的特点,在多因素多水平研究中可以大幅减少试验次数,在各研究领域都得到广泛应用。笔者选择加热频率、线圈与喷涂层距离、加热电流三个主要因素,确定三因素三水平正交表,正交试验因素和水平见表2。

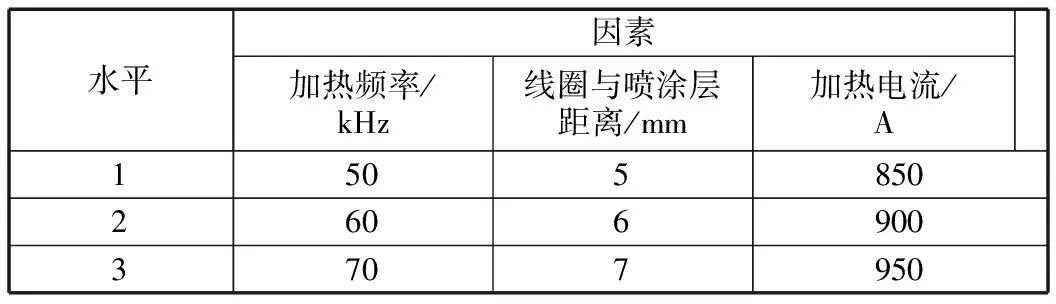
表2 正交试验因素和水平

根据表2设计正交试验,由L9(33)正交表得到九种变量组合,应用COMSOL软件进行三维瞬态求解,试验结果为仿线圈形状喷涂方案热板表面温差。正交试验结果见表3。

表3 正交试验结果

利用极差分析法对试验结果进行分析,见表4。极差R表示任意一列因素水平的试验指标最大值与最小值之差,Ti表示任意一列中水平i所对应的指标之和。由分析结果可知,仿线圈形状喷涂方案各因素对温差影响从大到小为线圈与喷涂层距离、加热频率、加热电流。

表4 极差分析

根据Ti的大小可以判断三个因素的最优水平,试验指标,即热板表面温差越小越好,因此应选择每个因素小指标所对应的水平。由表4可见,各因素的最优水平组合为加热频率60 kHz、线圈与喷涂层距离7 mm、加热电流900 A。

得出最优参数组合后,对仿线圈形状喷涂方案采用COMSOL软件进行三维瞬态模拟分析,得出热板表面温度分布云图,如图19所示。优化前后热板表面温度不均匀因数曲线如图20所示。

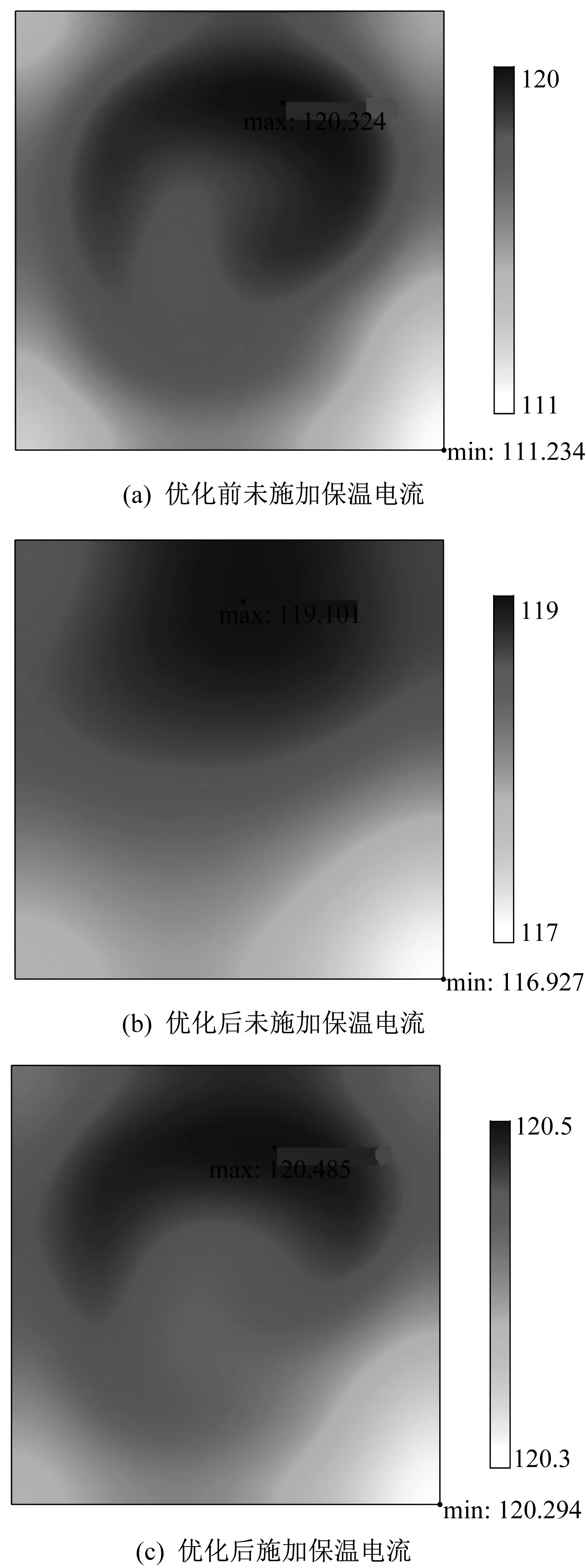
▲图19 热板表面温度分布云图

经正交试验极差参数优化后,未施加保温电流时,热板表面温差由为9.1 K减小为2.2 K。施加保温电流后,保温时间缩短,温差进一步减小至0.2 K,优化后的结果符合硫化行业标准。

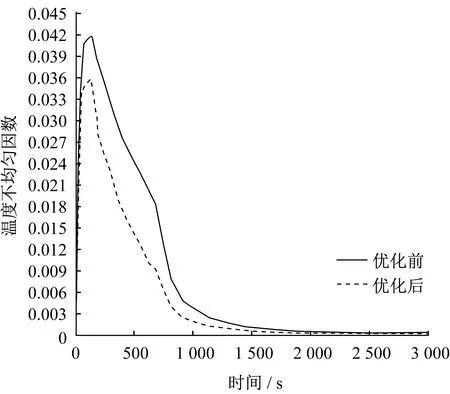
▲图20 热板表面温度不均匀因数曲线

5 结束语

为了研究电磁感应加热过程中硫化机热板温度场,采用COMSOL软件进行了仿真模拟,分析喷涂不同形状45号钢涂层加热效率与温差的关系、热板表面目标温度及喷涂尺寸与保温电流的关系、喷涂尺寸与加热速率的关系,并采用正交试验对最优方案参数进行优化,以达到减小温差的目的。

当热板表面目标温度从60 ℃提高到200 ℃时,保温电流从30 A增大到120 A。

通过不同喷涂方案喷涂45号钢涂层,在频率为50 kHz,加热电流为850 A,保温电流为110 A,线圈与热板距离为5 mm的条件下,菱形喷涂方案、全喷涂方案、三角形喷涂方案、仿线圈形状喷涂方案、圆形喷涂方案、正方形喷涂方案六种喷涂方案中,仿线圈形状喷涂方案加热效率最高,加热710 s后,热板表面温度可达到120 ℃。

利用正交试验与极差分析对仿线圈形状喷涂方案进行参数优化,各因素对温差的影响程度从大到小为线圈与喷涂层距离、加热频率、加热电流。用最佳参数组合进行模拟,在未施加保温电流时,温差由原来的9.1 K减小到2.2 K,在施加保温电流后,温差进一步减小至0.2 K。