有轨电车小半径曲线桥上无缝线路锁定轨温研究

狄怡霏，尹华拓，贾生旭，王卫东，罗信伟，吴 嘉，曾志平，唐启辉

(1.中铁十四局集团第五工程公司，山东 济宁 272117)(2.广州地铁设计研究院股份有限公司，广东 广州 510045)(3.中南大学土木工程学院，湖南 长沙 410075)(4.重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

现代有轨电车作为一种新型轨道交通工具，具有节约资源、导向性能好和减振降噪性能优越等优点[1-4]，自应用以来受到了世界各国广泛认可。

本文以成都某地小半径曲线桥上无缝线路为工程背景，通过ANSYS软件建立了35 m小半径曲线连续箱梁桥上扣件式无缝线路梁轨相互作用有限元分析模型，对比分别采用小阻力扣件、常阻力扣件和钢轨伸缩调节器时，线路纵向附加力和横向位移的变化，使有轨电车小半径曲线桥上无缝线路设计锁定轨温达到最优。

1 钢轨与扣件阻力模型建立

对桥上扣件式无缝线路的梁轨相互作用进行分析，并建立其计算模型。桥上扣件式无缝线路轨道结构采用小阻力扣件进行梁轨之间相互作用力的传递，在城市高架桥上铺设无缝线路后，其梁轨相互作用机理、影响因素、计算参数选取等都会发生变化[5-6]。本节主要阐述轨道各部件模型的建立。

1.1 钢轨模型

不同于普通铁路线路中常采用的UIC60钢轨，桥上小半径曲线纵向扣件式轨道结构采用60R2槽型钢轨[7]。分析梁轨相互作用下轨道结构力学特性时，钢轨采用空间梁单元进行模拟，钢轨截面采用60R2槽型钢轨标准断面[8]，如图1所示。

图1 60R2槽型钢轨标准断面

1.2扣件模型

桥上无缝线路梁轨之间产生的相对位移受到梁轨之间扣件提供的纵向阻力约束，同时扣件也在垂向对钢轨提供了均布支撑[9-10]，因此在计算附加纵向力时对扣件在纵向、垂向和横向的阻力都要进行考虑[11]。在扣件式无缝线路计算模型中，将扣件用非线性弹簧单元模拟[12]，分别考虑扣件在垂向和纵向的刚度，如图2所示。

图2 小阻力扣件纵向阻力

1.3 桥梁模型

以有轨电车35 m小半径曲线混凝土连续箱梁桥上无缝线路为研究对象，基于梁轨相互作用原理和有限元法，建立了有轨电车36 m+62 m+36 m小半径曲线桥上扣件式无缝线路梁轨相互作用有限元分析模型，如图3所示。

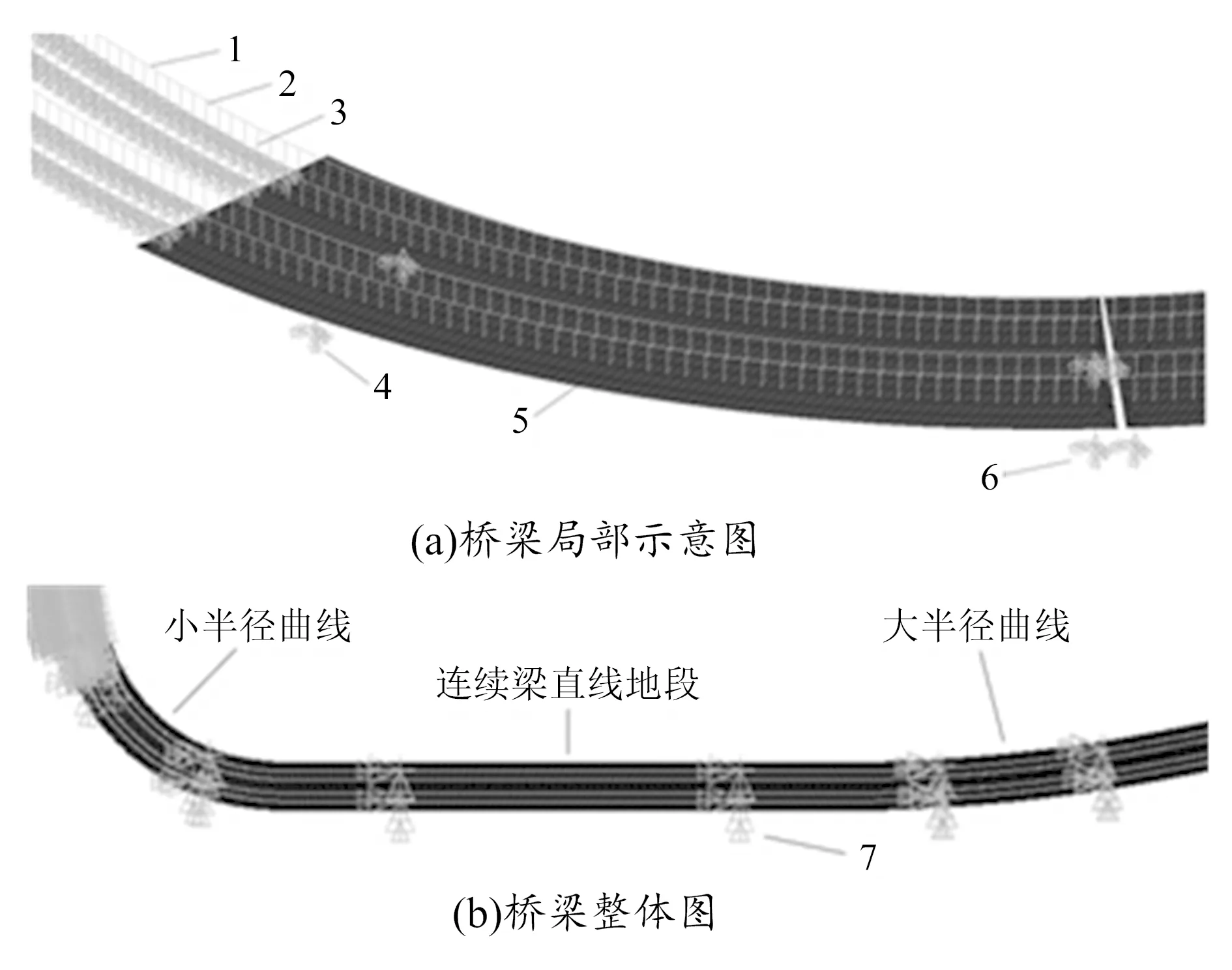
图3 桥梁图

在图3(a)中，1为钢轨空间梁单元；2为钢轨和桥梁上缘刚臂的弹簧单元(包含纵向非线性单元、横向和竖向线性单元)；3为刚臂单元，用于模拟桥梁上缘(下缘刚臂与桥墩相连)；4为活动支座，由路基节点和桥墩横向水平线刚度弹簧单元组成；5为桥面壳单元；6为固定支座，由路基节点、桥墩横向水平线刚度弹簧单元和桥墩纵向水平线刚度弹簧单元组成。在图3(b)中，从左至右为小半径曲线、连续梁、大半径曲线和简支梁，连续梁固定支座位于图中7位置处。

2 模型计算参数

本文主要分析桥上纵向扣件式轨道结构在梁轨相互作用下的力学特性，计算模型采用建立的力学分析模型，模型中主要结构的计算参数如下。

2.1 钢轨参数

60R2槽型钢轨采用U75V钢材，强度较高，钢轨的极限强度为472 MPa，安全系数为1.3，容许应力为363.1 MPa。钢轨基本参数见表1。

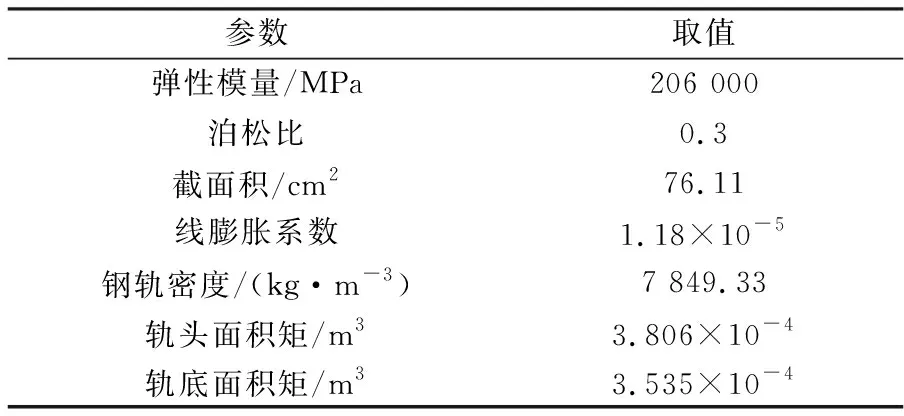
表1 60R2槽形钢轨基本参数

2.2 扣件参数

根据成都地区气象条件，本文所用YG-3型扣件的纵向阻力取气温20 ℃左右的实测值4.6 kN[13]，如图2所示。根据钢轨扣件三向刚度室内试验，测得扣件垂向刚度为43.4 kN/mm，横向刚度为25.5 kN/mm。根据扣件《铁路无缝线路设计规范》[14]，另取常阻力扣件纵向刚度为12 kN/mm。

2.3 桥梁参数

该轨道结构主要铺设于预应力混凝土连续箱梁上，模型中桥梁采用壳单元进行模拟，截面相关参数见表2。桥墩线刚度釆用弹簧单元进行模拟，根据文献[10]、[15]，简支梁桥墩顺桥向水平线刚度取值为500 kN/cm/线，连续梁固定墩顺桥向水平线刚度取值为1 200 kN/cm/线，桥墩横向水平线刚度为2 500 kN/cm/线。

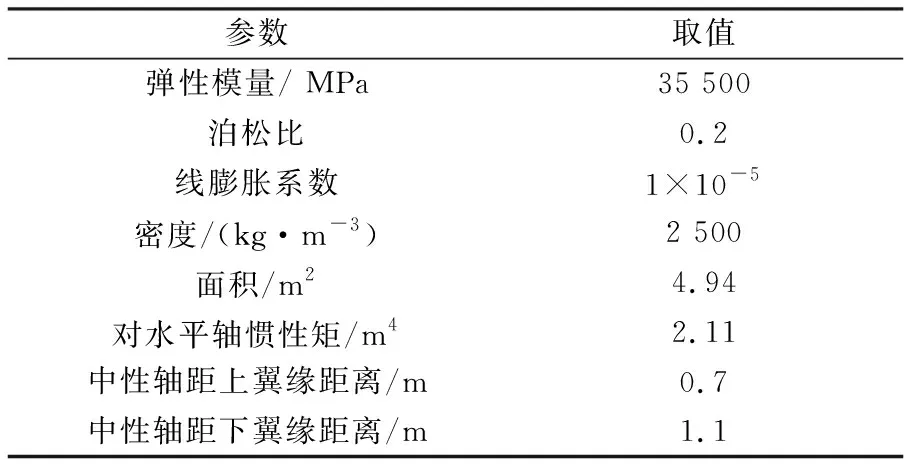
表2 连续箱梁计算参数

2.4 模型方案设置

无砟轨道桥上无缝线路的梁轨相互作用主要由钢轨扣件传递，因此采用不同种类扣件或钢轨伸缩调节对钢轨纵向附加力影响很大。本文基于该有轨电车轨道实际铺设情况，提出以下3种方案：方案一，全桥铺设常阻力扣件；方案二，在小半径曲线和大半径曲线地段铺设小阻力扣件，其余地方铺设常阻力扣件；方案三，由于连续梁端部位于曲线上，因此在方案二扣件布置的基础上，铺设单向钢轨伸缩调节器于连续梁内部活动支座处和连续梁固定支座处。

3 确定允许温降

3.1 伸缩附加力分析

根据文献[16]，无砟轨道混凝土梁温度差取值为30 ℃，对以上3种方案进行分析，如图4所示，选取每种方案中的最大伸缩附加压力和最大伸缩附加拉力，见表3。

图4 不同方案下伸缩附加力对比图

表3 不同工况下最大伸缩附加力 单位：kN

由图4和表3可知，升温或降温时，在连续梁中部和端部，轨道结构所受的伸缩附加力会达到一个峰值。通过比较3种方案的结果，发现铺设小阻力扣件对连续梁端钢轨伸缩力改善明显，对连续梁中部伸缩力改善不明显；方案三铺设钢轨伸缩调节器的效果与方案二相似。

3.2 允许温降分析

60R2槽型钢轨容许应力为363.1 MPa，有轨电车轴重为12.5 t，轴距为1.6 m，无砟轨道支座竖向刚度按43.4 kN/mm计算，最小半径曲线取35 m，最高设计时速为80 km/h。按照规范计算可以得到轨头压应力为92.0 MPa，轨底拉应力为99.0 MPa。其他纵向附加力按照模型计算结果取值。同时钢轨允许断缝值为70 mm。

根据上述条件，计算可得钢轨允许降温幅度，方案一为82.5 ℃，方案二为80.5 ℃，方案三为83.7 ℃。

由此可知，扣件铺设方式、种类和钢轨伸缩调节器对钢轨允许温降影响不大。

4 确定允许温升

4.1 轨道稳定性分析

无缝线路轨道稳定性主要受到道床阻力和轨道原始弯曲的影响，目前《铁路无缝线路设计规范》[14]并未给出统一的无砟轨道稳定性检算方法。因此本文控制钢轨横向绝对位移分别为1，2，…，10 mm，以钢轨允许温升作为评价指标，结合梁轨最大横向相对位移、桥墩位移和受力，综合考虑不同轨道稳定性要求对钢轨允许升温幅度的影响，如图5所示。

本文中模型的活动支座是顺桥方向的单向活动支座，即活动支座只允许桥梁纵向位移，而约束桥梁横向位移。

经计算，上述指标的最大值均发生在小半径曲线处。由图5(a)可知，在钢轨发生相同横向位移的情况下，采用钢轨伸缩调节器能允许更大的升温幅度。由图5(b)可知，是否采用小阻力扣件和钢轨伸缩调节器对梁轨横向相对位移影响很小。由图5(c)和(d)可知，在钢轨发生相同横向位移的情况下，采用小阻力扣件和钢轨伸缩调节器能减小桥墩位移和受力。

图5 不同钢轨横向位移对应的各项模拟结果

4.2 允许温升分析

根据3.2节中计算得到的轨头压应力92.0 MPa、轨底拉应力99.0 MPa和其他纵向附加力，算得强度条件确定的允许温升。结合3.1节中稳定性条件确定的允许温升，经计算比较得到钢轨允许升温幅度，见表4。

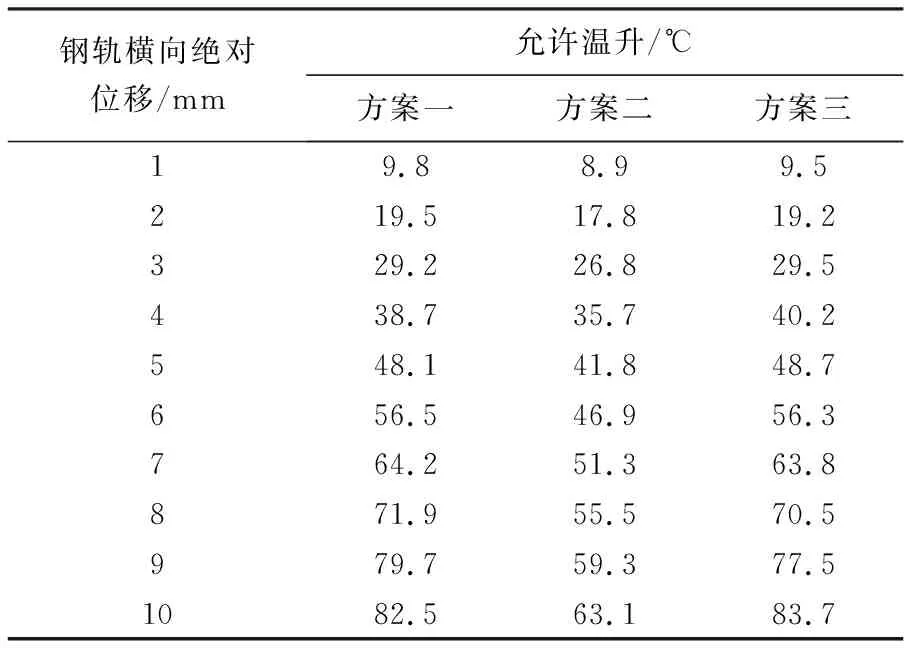
表4 钢轨允许升温幅度

5 锁定轨温设计

根据《铁路无缝线路设计规范》[14]，无砟轨道的设计锁定轨温由当地最高轨温、最低轨温决定，但本文研究线路处属于小半径曲线，轨道稳定性对锁定轨温可能有特殊影响，因此无缝线路设计锁定轨温的计算方法，按照有砟轨道的方法进行。

成都地区历年最高轨温57.3 ℃，最低轨温-5.9 ℃，修正值取±5 ℃，根据上文计算的允许温降值和允许温升值，按照规范计算可得小半径曲线桥上扣件式无缝线路轨道结构设计锁定轨温，见表5。

表5 不同钢轨横向位移下的设计锁定轨温

由表5可知，在小半径曲线地段，要求轨道稳定性越好，则锁定轨温越高。由于相同位移下，采用常阻力扣件和钢轨伸缩调节器时的锁定轨温，比采用小阻力扣件时的锁定轨温更高，因此在小半径曲线地段建议采用常阻力扣件和钢轨伸缩调节器。

6 结论

1)以成都市某有轨电车小半径曲线无缝线路的锁定轨温研究为例，可知两曲线间连续梁桥中部的附加力较大，建议有轨电车无缝线路设计时，要同时考虑梁端和梁中部的温度应力的释放与处理问题。

2)通过控制不同钢轨横向位移的对比研究，可知对比小阻力扣件，采用常阻力扣件或钢轨伸缩调节器对于维持线路的稳定性具有积极意义，因此在小半径曲线地段应该采用常阻力扣件或钢轨伸缩调节器，以达到维持线路稳定的效果。

3)在小半径曲线地段，桥墩横向位移和受力很大，使用小阻力扣件或钢轨伸缩调节器能有效减小桥墩横向位移和受力。若有轨电车线路对曲线矢度变化要求不高，可采用双向活动支座。

鉴于有轨电车线路的大范围铺设，本文的研究成果可为有轨电车小半径曲线桥上无缝线路锁定轨温设计与研究提供参考。