基于有限差分法的金属复合板冷却过程温度分布预测
李亚冠,王涛,2,武越,李志强,马更生
基于有限差分法的金属复合板冷却过程温度分布预测
李亚冠1a,1b,王涛1a,1b,2,武越1b,李志强1a,1b,马更生1a,1b
(1. 太原理工大学 a. 机械与运载工程学院;b. 先进金属复合材料成形技术与装备教育部工程研究中心,太原 030024;2. 太原重型机械(集团)有限公司,太原 030027)
研究金属复合板在冷却过程中的温度变化规律以及经过冷却后金属复合板的表面及内部温度分布规律。利用二维有限差分法对金属复合板材冷却过程中的温度变化规律进行了分析,从理论上推导了使用等步长节点法求解温度的差分方程,通过设置合理的边界条件解决了金属复合板基板和复板接触界面互相影响的传热问题。通过设置等步长节点的有限差分法计算得出金属复合板冷却过程的温度变化规律以及冷却后金属复合板的表面及内部温度分布,对比有限元软件模拟计算和有限差分程序计算结果,得出结论。界面处温度高,越靠近两边温度越低,通过与有限元软件模拟计算作对比,验证了差分法计算的准确性。
复合板;接触;冷却;有限差分法;温度场
有限差分法是工程计算中常用的一种数值计算方法,其基本思想是将求解问题的定义域划分为有限个网格,用有限个网格节点代替连续的求解域。在网格点上利用数值微分公式把微商换成差商,从而把原定解问题离散为差分格式,进而利用计算机来进行数值求解[1]。应用于轧制领域,可求解板材加热、轧制和冷却过程中的温度场变化以及轧辊在轧制和冷却过程中的热凸度变化等[2]。研究复合板冷却过程的温度分布,可以更加有效精确地制定轧制工艺,例如,确定轧件出炉到轧机的时长,以及轧后冷却时长的控制[3—4],精确控制轧制工艺[5],可以得到质量更优的轧制产品。
研究表明,微观上物体表面是粗糙不平的,因此一定载荷下,复合板基板和复板界面间的接触是不完全接触,实际接触仅发生在一些离散的点或微小的面积上,其余大部分是气体间隙或者其他杂质[5—7],如图1所示,a和b分别为基板和复板表面。实际应用中,将界面处的热流传递方式等效为一个合理的接触换热系数来进行计算[8],该系数大小与基板和复板的导热系数、接触面积、界面压力以及界面温度等都有关系,至今仍无法用理论公式进行精确计算,通常取值为10~30 kW/(m2·K)[9—10]。

图1 复合板接触面附近热流变化
1 二维导热微分方程
对于稳态传热,二维导热微分方程可表示为[11]:

式中:为温度(℃);为时间(s);为导热系数(W/(m2·℃));为密度(g/cm3);为比热容(J/(kg·℃));,为坐标。
有限差分法包括显式差分和隐式差分2种方式,其中显式差分法每个节点方程均可独立求解,而隐式差分法需联立每一层各个节点的方程组才可求解[12],因显式差分法计算简便,因此文中采用等步长显式差分法来求解复合板冷却过程的温度变化。
2 等步长显示差分法
等步长显式差分法中的等步长是指划分单元格的大小相等。实际生产中轧制所需的复合板,板材长度远大于其宽度和厚度,因此,计算复合板冷却过程的温度变化时,只考虑复合板宽度和厚度方向,利用二维有限差分法来计算冷却过程的温度变化。
对式(1)进行差分处理后得:

式中:T,j为节点(,)的当前温度(℃);T',j为节点或者单元(,)冷却Δ时间后的温度(℃);Δ为时间步长(s);Δ和Δ分别为和方向上的空间步长(mm)。

如图2所示,ABE1F1指基板,E2F2DC指复板,沿x轴(复合板宽度)方向平均划分为m个单元,单元大小为,节点总个数为m+1个,沿y轴(复合板厚度)方向平均划分为n个单元,单元大小为,节点总个数为n+1个。图2中直线箭头表示中心节点向接触界面节点传热情况,曲线箭头表示复合板表面向空气散热情况。
该方法中,采用基板和复板分别划分网格的方式。为了简化计算,基板和复板宽度方向划分相等的节点数。板材顶点处为1/4个单元大小,边界处为1/2个单元大小。计算基板和复板接触界面温度时,分别以对方接触边界的温度作为自身的边界条件,实现界面处温度互相传递的计算,计算时假设界面接触换热系数为一常数。
假设复合板外表面与外界环境为均匀冷却,考虑到辐射传热和与空气的对流换热[13],推导出复合板表面与空气接触的边界条件为:

式中:A和分别为空气温度和复合板外表面温度(K);为复合板宽度方向节点数;为复合板厚度方向总节点数;a为与空气的换热系数(W/(m2·℃));为辐射率,文中取0.8;为Stefan-Boltzmann常数,文中取5.67×10−8W/(m2·K4)。根据以上条件,推导出以下的差分方程:
1)基板内部:

2)复板内部:
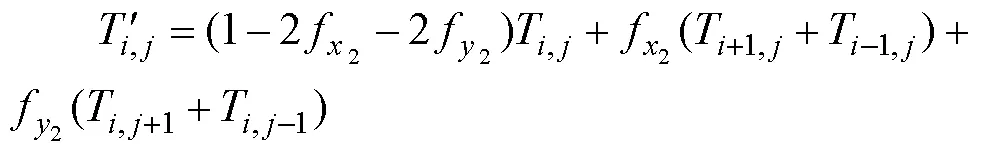
3)基板外表面:

4)接触位置基板表面:

5)接触位置复板表面:

6)复板外表面:

7)基板外部顶点:

8)接触位置基板顶点:

9)接触位置复板顶点:

10)复板外部顶点:

为了保证算法收敛,时间步长需满足以下条件:

式中:
3 计算分析
基于Microsoft Visual Studio平台,采用C#[14]语言编写了复合板冷却过程温度变化的计算程序,计算方法为有限差分法。基板的宽度和厚度分别为400 mm和20 mm,宽度和厚度方向步长分别为20 mm和2.5 mm,时间步长为0.02 s,其余计算参数如下:密度为7.8 g/cm3,比热容为662 J/(kg·℃),导热系数为300 W/(m·℃),复板的宽度和厚度分别为400 mm和10 mm,宽度和厚度方向步长分别为20 mm和2.5 mm,时间步长为0.02 s。其余计算参数如下:密度为7.8 g/cm3,比热容为462 J/(kg·℃),导热系数为60 W/(m·℃),空气换热系数为30 W/(m·℃),界面换热系数为30 000 W/(m·℃),基板复板的初始温度为1250 ℃,空气温度为25 ℃,冷却时间为20 s。
基于以上参数,利用有限元模拟软件ABAQUS,采用显示算法,计算了复合板冷却过程的温度变化,模拟时复合板界面处作如下处理:建立二维模型时,基板和复板界面分别用各自的边界,并且保证基板和复板沿宽度方向划分相同的单元数[14—15],单元格的划分方式如图3所示。为了验证该有限差分法计算的准确性,假设一个固定的界面接触换热系数进行计算。

图3 复合板网格划分
3.1 计算时间
采用相同的时间步长进行计算,有限差分法计算时间为1.406 s(程序运行时间),而有限元模拟时间为44 s(软件计算时间),可以看出有限元模拟计算所需时间远远大于有限差分法程序的运算时间。
3.2 计算结果
3.2.1 温度随时间变化变化
基板表面和复板表面及两板材接触界面处温度随时间的变化情况如图4所示,复合板不同位置处的温度均随冷却时间的增加而减小。从图4可以看出,有限差分法与有限元模拟的结果曲线几乎重合,说明2种方法计算结果比较吻合。
3.2.2 温度沿宽度方向变化
为了进一步对比等节点有限差分法与有限元模拟结果之间的差别,用冷却后温度在复合板不同位置沿宽度方向的分布情况来进行说明,沿宽度方向的温度分布如图5所示,给出了冷却以后基板表面、复板表面和接触界面处温度沿宽度方向的分布情况。复合板不同位置处沿板材宽度的分布均呈现中心高,边部低的趋势。从图5可以看出,有限差分法与有限元模拟的结果曲线几乎重合,吻合度较高,误差较小。
复合板冷却后整体温度分布云图如图6所示,可知,不同方法得出的复合板冷却后温度分布云图是一致的。对比冷却之后每种方法每个节点的温度值可知,有限差分法计算的结果与有限元模拟的结果温度差值最大不超过3.31 ℃,再次说明等步长差分法的计算结果与有限元模拟的结果比较吻合。

图4 采用不同方法计算复合板不同位置温度随时间变化情况

图5 复合板冷却后不同位置处沿宽度方向的温度分布

图6 采用不同方法计算复合板冷却后的温度分布云图
4 结论
1)采用基板复板边界温度互为对方边界条件的方式,差分法计算和有限元模拟所得的温度分布结果一致。
2)从运算时间来看,利用有限差分法编写程序计算的时间远小于有限元模拟计算所需的时间,并且差分法算法简单,占用计算机内存较小。
3)综上所述,利用有限差分法计算复合板冷却温度变化时,不仅算法简单、用时短、占用计算机内存小,而且计算结果比较精确,因此在实际轧制过程中,可优先考虑采用等步长节点法来进行计算。
[1] 辛启斌. 材料成型计算机模拟[M]. 北京: 冶金工业出版社, 2006: 5—15.
XIN Qi-bin. Computer Simulation of Material Forming[M]. Beijing: Metallurgical Industry Press, 2006: 5—15.
[2] 王涛. 热轧带钢板凸度和板形计算及预设定建模理论研究[D]. 秦皇岛: 燕山大学, 2012: 38—43.
WANG Tao. Theory Research on Strip Crown and Shape Calculation and Pre-set Modeling in Hot Rolling[D]. Qinhuangdao: Yanshan University, 2012: 38—43.
[3] 韩东序, 杜林秀, 吴红艳, 等. 轧后冷却速率对GCr15轴承钢球化组织的影响[J]. 东北大学学报(自然科学版), 2019, 40(10): 1392—1397.
HAN Dong-xu, DU Lin-xiu, WU Hong-yan, et al. Effect of Cooling Rate on Spheroidized Microstructure of GCr15 Bearing Steel[J]. Journal of Northeast University (Natural Science Edition), 2019, 40(10): 1392—1397.
[4] BHADESHIA H. Steels for Bearings[J]. Progress in Materials Science, 2012, 57(2): 268—435.
[5] 李大伟, 张磊, 周远航, 等. 2014铝合金轧制工艺研究[J]. 热加工工艺, 2020, 49(3): 110—112.
LI Da-wei, ZHANG Lei, ZHOU Yuan-hang, et al. Research on Rolling Process of 2014 Aluminum Alloy[J]. Hot Working Technology, 2020, 49(3): 110—112.
[6] 朱德才, 张立文, 裴继斌, 等. 固体界面接触换热系数影响因素的实验研究[J]. 锻压技术, 2008, 33(1): 139—142.
ZHU De-cai, ZHANG Li-wen, PEI Ji-bin, et al. Experimental Research of Influence Factors on Solid Interface Thermal Contact Conductance Coefficient[J]. Forging & Stamping Technology, 2008, 33(1): 139— 142.
[7] 石零. 低温固-固接触界面热传输研究[D]. 武汉: 华中科技大学, 2006: 66—81.
SHI Ling. The Investigation of Solid-Solid Contact Interface Thermal Transfer[D]. Wuhan: Huazhong University of Science and Technology, 2006: 66—81.
[8] TANG Q, HE J, ZHANG W. Influencing Factors of Thermal Contact Conductance between TC4/30CrMnSi Interfaces[J]. International Journal of Heat and Mass Transfer, 2015, 86: 694—698.
[9] 陈国学, 胡炜, 耿健. 复杂锻件净成形过程温度场的数值模拟[J]. 塑性工程学报, 1998, 10(4): 62—67.
CHEN Guo-xue, HU Wei, GENG Jian. Numerical Simulation of Temperature Fields in Net Shape Forming Process of Complex Forgings[J]. Journal of Plasticity Engineering, 1998, 10(4): 62—67.
[10] 朱智, 张立文, 顾森东. TC11钛合金与5CrMnMo模具钢间接触换热实验研究[J]. 大连理工大学学报, 2012(4): 509—513.
ZHU Zhi, ZHANG Li-wen, GU Sen-dong. Experimental Investigation of Contact Heat Transfer between TC11 and 5CrMnMo Die Steel[J]. Journal of Dalian University of Technology, 2012(4): 509—513.
[11] 梁勋国, 韩会全. 二维显式有限差分方法研究[J]. 钢铁技术, 2012(2): 19—29.
LIANG Xun-guo, HAN Hui-quan. Research on Two-Dimensional Explicit Finite Difference Method[J]. Steel Technology, 2012(2): 19—29.
[12] 陶文铨, 杨世铭. 传热学[M]. 北京: 高等教育出版社, 1982: 147—180.
TAO Wen-quan, YANG Shi-ming. Heat Transfer[M]. Beijing: Higher Education Press, 1982: 147—180.
[13] 陈超超, 邵健, 何安瑞. 热轧带钢温度场在线计算方法研究[J]. 机械工程学报, 2014(14): 135—142.
CHEN Chao-chao, SHAO Jian, HE An-rui. Research on Online Calculation Methods of Temperature Field of Hot Strip[J]. Journal of Mechanical Engineering, 2014(14): 135—142.
[14] 谭浩强. C程序设计(第四版)[M]. 北京: 清华大学出版社, 2010: 85—165.
TAN Hao-qiang. C Programming (Fourth Edition)[M]. Beijing: 2010: 86—165.
[15] 李世芸, 张曙红, 张代明. 双金属复合带材轧制过程有限元模拟[J]. 中国有色金属学报, 2001, 11(6): 1075.
LI Shi-yun, ZHANG Shu-hong, ZHANG Dai-ming. Finite Element Simulation of the Rolling Process of Bimetallic Composite Strip[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(6): 1075.
Prediction of Temperature Distribution of Metal Composite Plate during Cooling Process Based on Finite Difference Method
LI Ya-guan1a,1b, WANG Tao1a,1b,2, WU Yue1b, LI Zhi-qiang1a,1b, MA Geng-sheng1a,1b
(1. a. College of Mechanical and Vehicle Engineering; b. Engineering Research Center of Advanced Metal Composites Forming Technology and Equipment, Taiyuan University of Technology, Taiyuan 030024, China; 2. Taiyuan Heavy Machinery (Group) Co., Ltd., Taiyuan 030027, China)
The work aims to study the temperature change law of metal composite plate during cooling and the distribution law of surface and inside temperature after cooling. The two-dimensional finite difference method was used to analyze the law of temperature change of metal composite plate during cooling, and the difference equation for solving the temperature by equal-step node method was theoretically derived. Reasonable boundary conditions were set to solve the heat transfer problem of the interaction between the metal composite plate substrate and the contact interface of the composite plate.Through the finite difference method with equal-step node, the law of temperature change of the metal composite plate during cooling and the distribution of surface and inside temperature after cooling were calculated. By comparing the simulation results of finite element software with those of finite difference program, a conclusion was drawn. The interface temperature is high, but the temperature closer to both sides is lower. Compared with the simulation calculation by finite element software, the accuracy of the difference method is verified.
composite plate; contact; cooling; FDM; temperature field
10.3969/j.issn.1674-6457.2021.06.008
TG335.81
A
1674-6457(2021)06-0064-06
2021-07-01
国家自然科学基金(51905372)
李亚冠(1995—),男,硕士生,主要研究方向为复合板轧制工艺。
王涛(1985—),男,博士,教授,主要研究方向为轧制工艺与智能装备。

