大藤峡水利枢纽工程泄水闸基础稳定性研究

王德库,谭 春,隋 伟

(1.中水东北勘测设计研究有限责任公司，吉林 长春 130000； 2.水利部寒区工程技术研究中心，吉林 长春 130000)

1 工程概况

大藤峡水利枢纽工程水库正常蓄水位61.00 m，汛期限制水位47.60 m，防洪运用最低水位44.00 m，设计低水位47.60 m。水库总库容为34.79亿m3，防洪和补水压咸库容均为15亿m3，设置完全低于正常蓄水位。船闸规模为3 000 t级。电站装机容量1 600 MW，8台机组，多年平均发电量60.55亿kW·h，保证出力366.9 MW。

大藤峡水利枢纽的选定坝址具有以下特点：1)坝址处河床覆盖层薄，岩层较薄且缓倾向下游偏左岸，呈泥岩与砂层软硬互层产出。2)软弱夹层、断层发育且连续性较好，软弱夹层产状与岩层产状基本一致，断层陡倾。3)砂岩节理裂隙发育，包括两组陡倾共轭节理。大藤峡水利枢纽的泄水闸闸门推力较大，采用两孔一联的结构布置，结构相对单薄，初步分析坝基滑移模式以深层滑动为主，前段可沿软弱夹层发展，而滑移后段无明显贯穿地表的缓倾结构面，故在坝基推力及重力的作用下，下游岩层可能剪断岩石，也有可能沿上述陡倾共轭节理折断，进而产生贯通性破坏面，影响坝体的整体稳定性。

2 三维裂隙网络模拟

岩体中的结构面对岩体的强度与变形的重要作用早已为业界认识，但是现场实测的裂隙仅是在露头面上采集的，是二维的，仅用露头面这部分裂隙是无法完整地反映出岩体内部裂隙在三维空间中的发育特征。三维裂隙网络模拟则可以求解出裂隙的一些参数，如平均迹长、平均产状、密度等，从而获得三维空间内裂隙的展布特征。

根据现场收集的地质特征资料，针对D1y1-2与D1y1-3地层进行了三维裂隙网络模拟，模拟结果示意图如图1所示。

在三维裂隙网络中建立了若干与坝轴线垂直的裂隙连通率计算剖面，采用Dijkstra算法搜索最短路径的方法，算得D1y1-2与D1y1-3地层的裂隙连通率为(40±5)%。利用计算出的连通率数据，确定了断续裂隙的等效力学参数，如表1所示。

表1 断续裂隙的等效力学参数表

对于切向刚度、法向刚度、水力学参数等参数，我们直接采用结构面的相应参数作为断续裂隙的等效参数。这是因为，这些参数受裂隙的分布影响非常大，且岩体内部裂隙分布具有高度随机性与复杂性。为工程安全起见，我们不采用完整岩石与裂隙的参数加权，而是直接使用裂隙参数进行后续分析计算。

3 数值模拟计算

本节采用UDEC6.0软件进行数值模拟。面对含有结构面系统并且地质条件相对复杂的大坝坝基，很难在三维层面对其全面了解，因此决定利用UDEC6.0软件在二维尺度建立模型。并且诸多学者研究证明，二维分析结果是更为保守的。由现场工程地质条件可知，28号坝段节理裂隙十分发育，且倾向垂直于坝轴线，对坝段的稳定性造成十分不利的影响，所以最终选了28号坝段进行稳定性分析。在UDEC6.0软件中建立对应的泄水闸与天然地质体，数值模型如图2所示。

3.1 正常工况模拟

按照设计要求，正常蓄水工况的水位如表2所示。

表2 正常工况水位表 m

根据常规的判别方式，当出现以下两种情况时可以认为该结构处于达到极限平衡：1)最大不平衡力稳定并趋近于零；2)所有监测点变形值稳定至一常数，并最后保持不变。按照上述准则进行模拟。

计算过程中，为了确保计算结果的准确性设置了大量的监测点，其中选取了5个关键监测点，分别用A，B，C，D，E表示5个所选关键监测点的位置，以便于表达关键监测点的具体位置和下文的描述，如图3所示。

这5个关键监测点是最有可能发生破坏的区域，分别是闸室及其底部基岩、左右齿槽基岩以及下游近地表基岩，监测其x,y方向位移的变化。计算结果为关键监测点位移变化值随计算时步的变化曲线，结果表明三个工况下模型均达到了稳定平衡状态。

3.2 超载工况模拟

坝基稳定性可以用超载系数表征。作用于坝上的外荷载强度由于特殊原因可能超过设计荷载，因此使混凝土坝失稳或遭到破坏。建筑物失稳或遭到破坏时的外荷载与设计正常荷载强度之比，即KP=P/P0，称为结构超载系数，用KP表示。超载法计算的基本方法需要以如下假定为基础：假定坝基岩体强度参数不变、假定结构面强度参数不变。计算过程为逐级超载加载上游水荷载，分析坝基变形直至破坏的演变发展过程与超载倍数的关系，确定坝基在失稳时相应的超载倍数。

在正常蓄水工况下，即上游水位61 m，下游水位22.71 m，通过逐倍超载上游水压力荷载，分别模拟28号坝段在正常荷载(1倍荷载)、2倍荷载、3倍荷载等下坝基的稳定性，荷载加载方式示意图如图4所示。逐级加载，直到整体发生破坏，模型破坏的判定依据是从位移变形和最大不平衡力这两个方面考虑的，最后分析研究其稳定性水平。

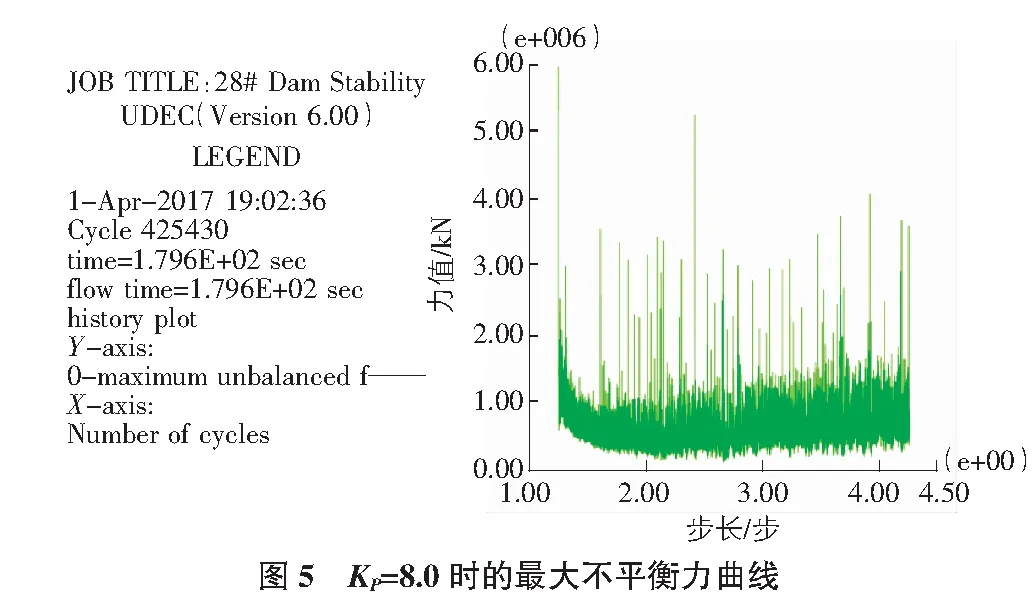
结果表明，当超载系数KP=1.0，2.0，3.0时，其最大不平衡力曲线最终都趋于零，且模型没有出现塑性区，模型内各点位移也都很小，最后都趋于一个数稳定，说明模型没有发生破坏。随着超载系数的逐级增加，当超载系数KP=7.0时，模型的x向和y向位移都有所增加，相比KP=6.0，其中闸室、两齿槽基岩的位移增加速率有所增大，但最后的位移亦都趋于一个稳定值。当超载系数KP=8.0时，模型整体发生破坏。当超载系数KP=8.0时，从图5可以看出，在计算过程中其最大不平衡力不再处于相对稳定状态，而是波动明显，说明该结构已发生破坏失稳。

4 结论

1)坝基岩体的软弱夹层与节理裂隙对于泄水闸破坏起到决定性作用。其中，软弱夹层间距2 m～5 m，产状与层面产状一致。而坝基的节理裂隙中发育大量近垂直于剖面的裂隙，总体倾向上游，倾角为79°，间距为2 m，对泄水闸稳定性起到关键作用。

2)以三维裂隙网络模拟手段为基础，生成了D1y1-2与D1y1-3地层内的三维裂隙，采用Dijkstra算法确定了D1y1-2与D1y1-3地层的连通率为(40±5)%，进而确定了断续裂隙的等效力学参数。

3)在超载阶段，数值模拟位移值随着超载量的增大逐步增加。当KP=4.0时，泄水闸模型产生塑性形变;当KP=8.0时，泄水闸模型发生大位移，整体发生破坏。泄水闸与地基整体稳定性较好。