面对称高速飞行器横侧向耦合失控特性

孙春贞, 黄一敏

(南京航空航天大学自动化学院, 江苏南京 210016)

引 言

通道间耦合面是对称飞行器的典型特点, 尤其是滚转-偏航通道间的耦合. 与低速飞行器相比, 面对称高速飞行器Mach数、 迎角、 高度、 动压变化范围很大, 不稳定性、 强耦合性、 强非线性、 强不确定性相互叠加, 严重影响了飞行器的稳定性, 尤其是高空大迎角飞行时, 通道间耦合严重, 并且横航向表现为严重的非最小相位特性, 这对控制系统的设计提出了严重的挑战.

面对称飞行器发展史上, 从X系列超声速飞行器验证机到X系列重复使用飞行器验证机, 从航天飞机到再入飞行器, 耦合动力学特性带来的影响都是飞行器研制和发展过程中不可忽略的部分[1]. 航天飞机初期再入过程中存在严重的荷兰滚耦合和控制耦合, X-37B和HTV-2飞行器也存在耦合引起横航向的稳定与控制问题, 这些耦合都严重影响了飞行器的稳定性和可控性[2-5].

针对耦合带来的失控问题, 从X系列验证机开始, 科研人员一直在研究其耦合机理， 从气动设计和寻求新的耦合控制策略两方面展开研究, 以减小飞行器失控的可能性[1-11]. 针对耦合带来的非最小相位特性, 在控制方面也取得了一些可以借鉴的成果[2-16]. 但是由于飞行器动力学特性复杂, 耦合带来的控制问题更为复杂, 需要系统梳理耦合对高速飞行器运动控制的影响.

本文主要针对面对称高速飞行器横侧向存在的典型耦合导致的非最小相位特性, 研究耦合特性分析方法, 分析其耦合机理, 研究耦合失控特性.

1 耦合动力学模型

面对称飞行器偏航-滚转通道之间存在气动耦合、 运动耦合、 惯性耦合以及操纵耦合, 这4类耦合相互作用, 相互激发. 为了分析偏航-滚转通道的耦合模态特性, 建立小扰动线性化的耦合动力学模型. 线性化时主要考虑运动耦合、 操纵耦合以及迎角对横侧向的耦合影响. 横侧向小扰动线性化耦合动力学方程可以描述为状态空间的形式

其中, 小扰动状态x=[β,p,r,φ], 小扰动控制量u=[δa;δr],β,p,r,φ分别为侧滑角、 滚转角速率、 偏航角速率和滚转角,δa,δr分别为副翼和方向舵.

定义侧力Y、 滚转力矩L和偏航力矩N对不同状态的偏导数

小扰动线性化模型可以具体描述为

式中,g是重力加速度,V是速度,α是迎角,θ是俯仰角. 利用小扰动线性化模型可以分析滚转、 偏航通道的耦合模态.

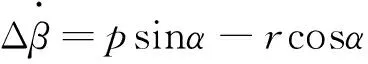
耦合模态分析主要考虑这两类耦合的影响.

2 控制耦合模态特性分析

滚转、 偏航通道主要有2个耦合模态: 荷兰滚耦合模态、 控制耦合模态. 荷兰滚耦合模态描述了飞行器自身的运动特性, 在很大程度上表征了横侧向的运动稳定性, 控制耦合模态反映了控制输入对横侧向运动的耦合影响. 利用小扰动线性化模型, 推导耦合模态的数学描述, 分析耦合模态的特性.

2.1 数学描述

为了分析耦合模态的特性, 推导舵面到滚转角速率的传递函数, 传递函数的分母多项式可以表征荷兰滚耦合模态, 分子多项式可以反映控制耦合模态的特性.

利用线性化小扰动模型, 横侧向运动的特征方程可以描述为

副翼到滚转角速率的传递函数可以描述为标准形式

(1)

式中,kδa为传递函数的增益,ξφ,ωφ分别是控制耦合模态的阻尼比和频率,ξdr,ωdr分别为荷兰滚模态的阻尼比和频率,ξsr,ωsr分别是滚转/螺旋模态的阻尼比和频率.

根据Clam法则, 副翼到滚转角速率的传递函数可以描述为

(2)

利用式(2)推导传递函数(1)的具体表达式.

计算A*可以得到控制耦合模态固有频率的近似解析

控制耦合模态和荷兰滚耦合模态的固有频率直接与迎角、 滚转力矩L/偏航力矩N/侧力Y对侧滑角的偏导数有关, 直接反映了耦合模态的稳定性, 是分析耦合模态的关键参数.

控制耦合模态和荷兰滚耦合模态对应的传递函数的零极点可以描述为

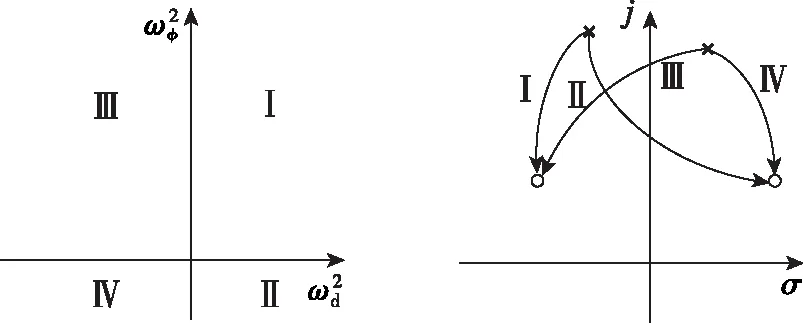
图1 零极点的相对位置示意图Fig. 1 Root map

2.2 控制耦合模态特性分析

控制耦合模态的偏离参数主要与迎角、 偏航稳定导数、 滚转稳定导数、 动导数、 操纵面效率有关, 不考虑动导数的影响, 可以简化为

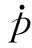
滚转偏航稳定比ηβ从飞行力学的角度描述了单位侧滑角产生滚转和偏航能力的强弱, 也描述了偏航与滚转之间的耦合程度, |ηβ|越大, 滚转偏航耦合程度越大.

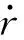
滚转偏航操纵比ηa从飞行力学的角度描述了单位操纵面产生偏航和滚转能力的强弱, 也描述副翼操纵对偏航通道的耦合影响, |ηa|越小, 说明副翼对偏航的耦合影响越大.

(3)

时, 副翼到滚转角速率的传递函数为最小非相位系统, 利用副翼控制滚转可能会引起滚转反向, 进而导致滚转发散; 若副翼对偏航通道产生的耦合力矩满足

(4)

时, 副翼到滚转角速率的传递函数为最小相位系统, 在控制能力范围内, 利用副翼控制滚转不会引起滚转反向.

(5)

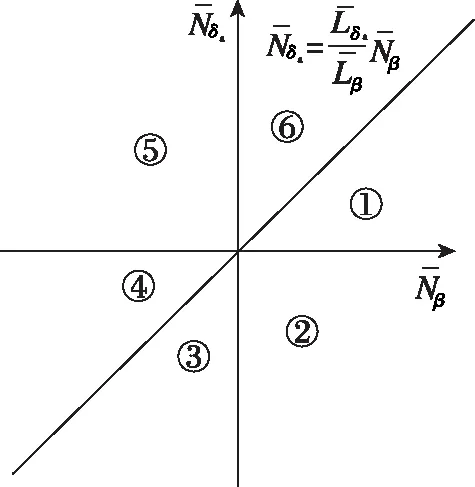
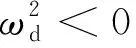
图2 和的相对位置关系

针对滚转静稳定的飞行器, 利用式(3)～(5), 分析航向静稳定性导数和副翼对偏航的耦合力矩导数对滚转控制稳定性的影响, 存在以下几种情况:

根据上述分析, 对于航向静稳定的飞行器, 非最小相位特性主要取决于副翼产生不利偏航的耦合力矩; 对于航向静不稳定的飞行器, 非最小相位特性是二者综合作用的结果, 控制律设计时需要考虑非最小相位的影响.

3 耦合失控特性分析

航向静不稳定和副翼对偏航的不利耦合是导致耦合失控的关键因素, 因此改善航向稳定性、 抑制副翼对偏航的耦合影响是耦合控制的基本思想. 考虑用方向舵增加航向稳定性, 其控制律可以简单描述为

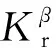
若增稳后的系统满足

则系统变为最小相位系统, 不存在控制偏离现象.

但是对于高速飞行器, 方向舵效率低, 当荷兰滚不稳定, 且副翼对偏航存在不利耦合影响时, 二者均需要通过方向舵改善其不利影响, 这种耦合控制策略对方向舵的需求大, 方向舵一方面用于航向增稳, 抑制滚转过程中的侧滑, 另一方面还需抑制副翼对偏航的耦合, 当侧滑角较大时方向舵易饱和, 导致滚转失控, 控制的鲁棒性差, 对不确定性的适应能力差.

对于不稳定的荷兰滚耦合模态, 其闭环系统稳定导数为

在荷兰滚模态增稳的基础上进行滚转控制, 滚转角速率反馈到副翼后的闭环系统稳定导数为

为了抑制滚转失控, 需要控制滚转角速率和侧滑角. 图3给出了滚转控制过程飞行状态响应示意图.

图3 滚转控制过程状态响应示意图Fig. 3 State variation during controlling roll attitude

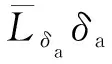
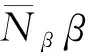
4 典型算例

根据第3节的分析, 为了抑制滚转失控, 需要控制滚转角速率和侧滑角, 滚转角速率越大, 侧滑角越大, 越容易引起滚转失控. 为了验证此结论, 针对飞行器荷兰滚耦合模态不稳定, 且存在控制耦合偏离现象的情形, 进行仿真分析.

针对滚转控制律

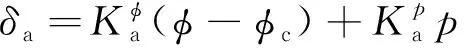
设计了两组控制律参数, 控制律1用于模拟失控现象, 控制律2为正常控制律. 控制律2副翼偏转角度小, 滚转过程中滚转角速率和侧滑角小; 控制律1副翼偏转角度大, 滚转过程中滚转角速率和侧滑角较大, 模拟失控现象, 图4～9为仿真结果图.

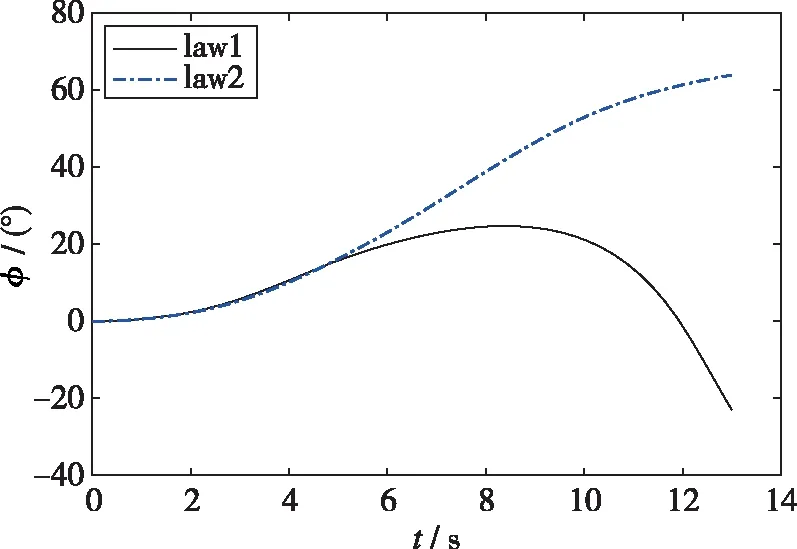
图4 滚转角变化曲线Fig. 4 Roll attitude variation

图5 侧滑角变化曲线Fig. 5 Sideslip angle variation

图6 滚转角速率变化曲线Fig. 6 Roll rate variation

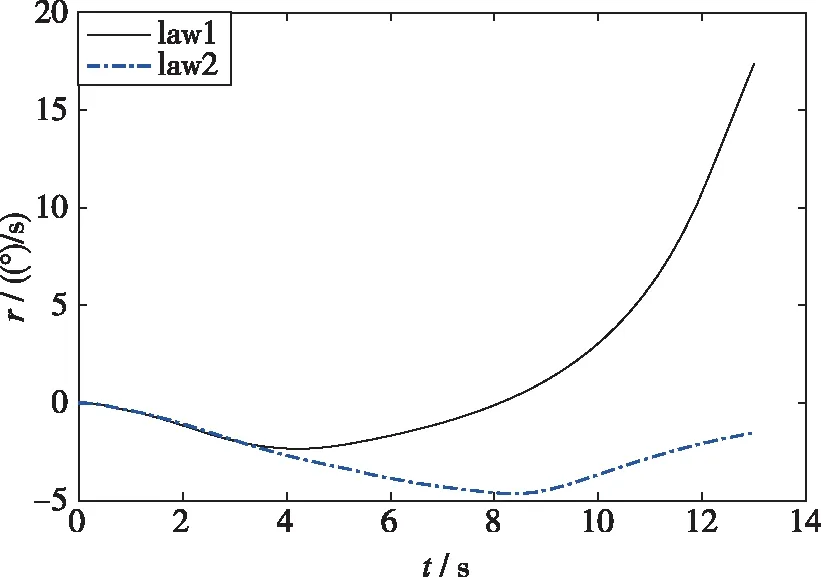
图7 偏航角速率变化曲线Fig. 7 Yaw rate variation

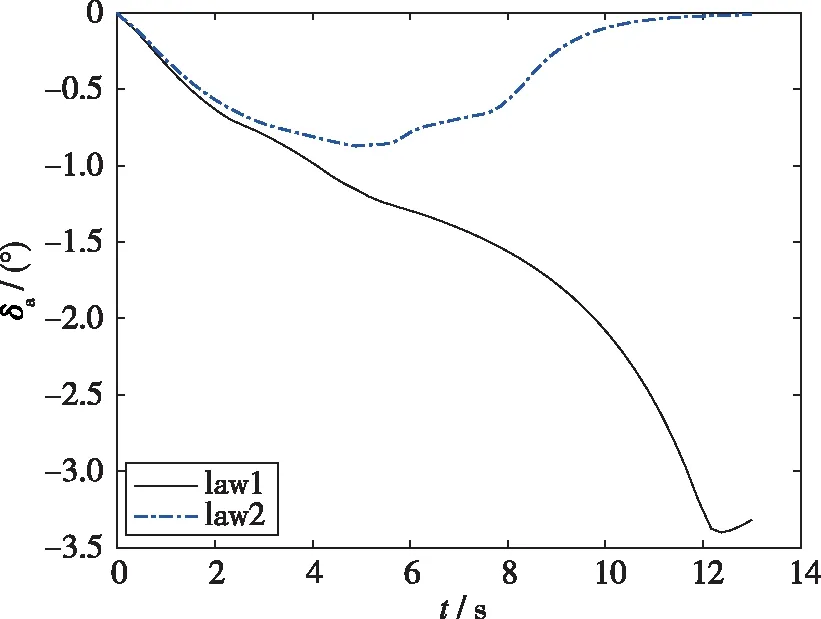
图8 副翼变化曲线Fig. 8 Aileron variation

图9 方向舵变化曲线Fig. 9 Rudder variation

采用控制律1控制飞行器右滚转, 滚转开始2 s 内副翼偏转角度略大于控制律2, 侧滑角二者几乎相同, 2 s以后小于1°, 副翼偏角逐渐增大, 方向舵饱和, 方向舵控制能力在临界状态, 随着侧滑角的增加, 方向舵控制能力不足, 荷兰滚耦合模态不稳定, 侧滑角进一步增加, 产生逐渐增加的负滚转力矩, 为了跟踪预定的滚转角指令, 副翼偏转角度增加, 产生不利的偏航力矩, 进一步增加了侧滑角增大的趋势, 当侧滑角大于1°时, 侧滑产生的负滚转力矩大于控制力矩, 滚转反向.

采用控制律2滚转过程中副翼偏转角较小, 侧滑角小于1°, 副翼偏角较小, 方向舵能力在临界状态, 随着滚转角的增加, 副翼减小, 方向舵需求减小, 系统处于稳定状态.

5 结论

本文针对面对称高速飞行器横侧向存在的典型耦合, 提出了基于滚转偏航稳定比和副翼滚转偏航操纵比的耦合模态分析方法, 给出了基于副翼-偏航耦合描述的控制耦合偏离边界条件, 该方法为飞行器横侧向耦合失控边界分析提供了一种近似解析解. 若面对称高速飞行器荷兰滚耦合模态不稳定, 且存在控制耦合偏离现象, 利用副翼控制滚转, 耦合控制对方向舵的需求大, 当达到失控边界时, 方向舵饱和, 滚转失控. 仿真结果验证了该耦合失控分析方法的有效性.