视觉与微惯导系统中多传感器信息融合导航方法研究

王海，刘峰寰

沈阳理工大学

针对视觉与微惯导系统在无人机等领域应用为研究背景，研究了在视觉微惯导系统中基于多传感器信息融合的姿态测量方法。测试结果为视觉与微惯性传感器姿态测量方法融合，以融合测姿结果作为观测数据，随后通过卡尔曼滤波器进一步准确估计载体姿态。采用研制的视觉与微惯导组件搭建了实验平台，并进行载体姿态测量实验，最后简单验证了融合算法的有效性。

同步定位与地图构建（SLAM）越来越广泛地应用到地面移动机器人、水下机器人、无人机乃至行星探测等领域，是当前工业界和学术界备受关注的热门研究方向。SLAM技术是指某种特定的载体，搭载了一种或多种不同的传感器，在环境先验未知的情况下，在运动过程中实现自身的定位以及周围环境的建图。

导航的前提就是定位与建图，在不同应用场景下实现定位与建图，需要引入不同的传感器。激光雷达和视觉（Visual）是两大类根据所用传感器不同而流行的SLAM主要方法。基于激光雷达的SLAM方法能够获取高精度的地图，但存在价格昂贵、空间分辨率低等缺点。基于视觉的SLAM方法依赖的传感器具有体积小、功耗低、场最辨识能力强及感知纹理信息丰富等优点（视觉SLAM技术的进展与应用），但对于环境纹理特征不明显及图像采集帧率很快的情况，其运动估计能力会降低。

低成本视觉微惯导集成模块的设计

在特殊环境下，实验室自主设计了一套完整的视觉与微惯导融合系统的位姿检测，包括数字信号开发板（Raspberry Pi 4B）、 电 源 模 块、 摄 像 头 模 块、GY-85模块等。摄像头模块使用手机自带摄像头及单目摄像头，MPU6050模块通过惯导解算得到六自由度的位姿信息。利用扩展卡尔曼滤波算法对这两个通道的姿态结果进行融合，并得到姿态估计结果。

多传感器姿态测量方法

视觉传感器以及陀螺仪、加速度计、磁阻传感器共同构成了视觉与微惯导融合系统。四元数和欧拉角方法可通过陀螺仪输出完成姿态更新，求解载体的横滚、俯仰和偏航角度。解析加速度计的输出并进行计算，以获得俯仰和滚转角的两个主要情况。在纹理不丰富或高动态视觉丢失的情况下，在单目相机初始化时，由于单目初始化只能得到深度的初值，无法得到绝对尺度信息，只能取到所有特征点的深度中值。不同微惯性器件有着不同噪声的频率特点，视觉与微惯导在不同环境有着各自的优势，多重数据通过互补滤波器的融合，提升了载体姿态测量的精准度。

多传感器信息融合与滤波算法

通过视觉与微惯导解算均可获得位姿信息，视觉方法依赖的传感器具有体积小、功耗低、场最辨识能力强及感知纹理信息丰富等优点，但对于环境纹理特征不明显及图像采集帧率很快的情况，其运动估计能力会下降。微惯导解算短时、定位精度高、自主性强，同时可以完全基于加速度计与陀螺仪完成位姿解算，在纹理特征不明显或快速运动的情况下可以达到良好的测量效果。通过卡尔曼滤波实现两者的信息融合，一方面，相机在运动过程中可以确定出位姿以及能够为周围环境建立出3D模型；另一方面，由于微惯导通过解算可以直接获得自身的运动信息，与视觉融合时能够为其提供重力方向，同时也使横滚与俯仰角可观，能够达到更精确及鲁棒的运动估计。

图1 系统框图。

特征提取、匹配、筛选

OFAST相比较其他算法，拥有尺度的旋转和描述。类似计算重心指向更亮的区域，计算角度、图像梯度。搭建图像金字塔并在金字塔不同层的每一层分别提取一个FAST，可以得到多种尺度下的FAST特征。在这种情况下，可以认为FAST具有一定程度上的尺度不变性。根据特征点的方向计算旋转后的BRIEF描述子，使其具有旋转不变性。

特征匹配是对两帧图像间的描述子进行匹配，提供给后续位姿估计。假设分别在图像1、2中提取到相同个数的ORB特征点，然后计算对应的BRIEF描述子。ORB的特征匹配常用暴力匹配法进行，即对第一个图中的一个特征点与第二个图中的每一个特征点测量BRIEF描述子的汉明距离，对这些汉明距离进行排序，设定小于一定阈值的点对作为匹配点。

图2 经过筛选后的匹配。

暴力匹配的操作简单，但是结果会存在大量误匹配，误匹配影响着后续的位姿估计的速度以及精度。使用暴力匹配，然后根据距离应相等或相近的正确匹配点对进行提纯，提高匹配的准确度，以减少运行时间及提高相机运动解算的精度；再使用Lowe’s算法，获取第一个图中有误匹配的关键点，并找到第二个图中在暴力匹配时得到的误匹配的两个关键点中欧式距离最近的那个，如果最近的关键点的欧式距离与另外一个关键点的欧式距离之比小于预设的阈值，那么接受这一对匹配点。最后利用筛选后的特征点对构建非线性优化问题，求解变换矩阵。

位姿估计

单目视觉里程计中，常通过经过筛选后的匹配并根据对极几何以及本质矩阵等理论，估计出粗略的运动。为了提高这种粗略运动估计的准确性，基于将优化问题表现成图的形式的理论进行帧间运动估计，在帧间运动估计问题中，可将不同时刻的相机位姿和路标点视为顶点，不同位姿之间的关系当成边。对于帧间的运动估计和尺度未知的特征点位置解算问题，可基于图优化理论进行解算。

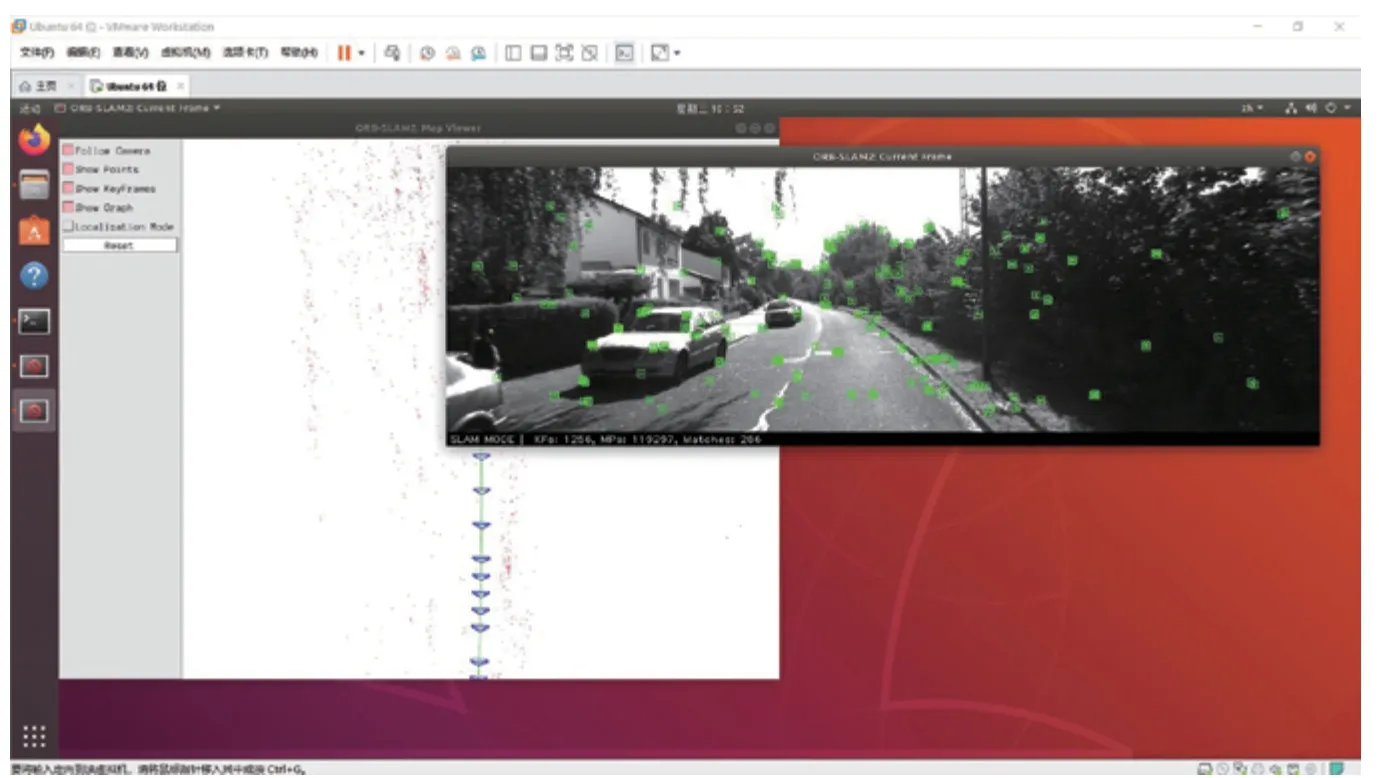
图3 运行过程。

假设帧间运动R，t，相机内参矩阵为K，特征点的世界坐标为Xi，两相机坐标系下的相机坐标分别为Ci1、Ci2，对应的深度值分别为S1、S2，相机1的位姿为单位矩阵，根据投影关系，有：

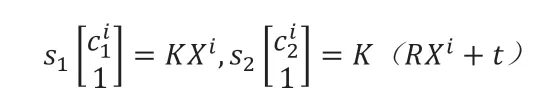
然而由于噪声影响，投影关系不能准确成立，用二范数量化每一个特征点存在的误差，并对所有特征点的误差项进行求和，可得目标优化问题如下。

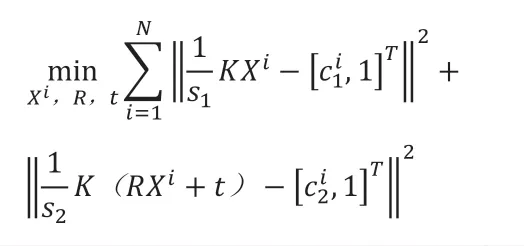
也称最小化重投影误差问题，为非线性、非凸的优化问题。实际的求解过程中是调整每个Xi，使得每个误差项都尽量地小，因此也可称为捆集调整（bundle adjustment，BA）。

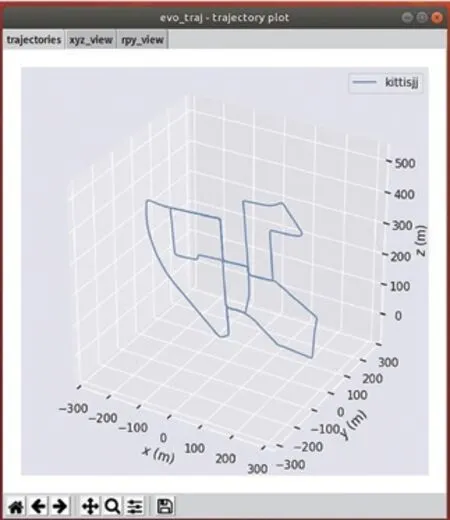
图4 轨迹图。

求解两帧之间的运动，需设置相机位姿结点、特征点的空间位置结点，以及重投影误差边。优化求解前，需要选择求解器和迭代算法：①选择线性方程求解器；②选择块求解器；③选择列文伯格-马夸尔特（Levenburg-Marquadt，LM）迭代算法。

为解算各帧的估计位姿，帧间运动估计过后，根据数据集中的连续帧，首先固定第一帧的位姿，利用估计出的运动进而推算出接下来各帧的估计位姿。

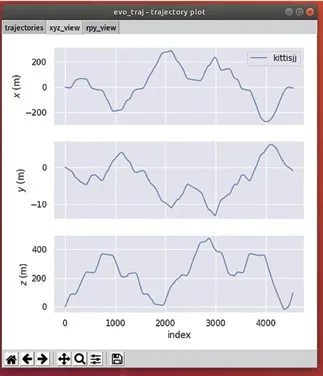
图5 方向示意图。

实验结果

本文试验采用了kitti数据集进行测试和评估，它包含了市区、乡村和高速公路等场景采集的真实图像数据，每张图像中最多达15辆车和30个行人，还有各种程度的遮挡与截断。以10Hz的频率采样及同步。

结论

本文以无人机在无卫星条件下的位姿估计为背景，设计了一个多传感器组合定位系统，其中包括单目视觉传感器、IMU，实现了视觉与惯导的融合定位。提出了基于最小二乘法实现单目视觉尺度的最优估计; 基于扩展卡尔曼滤波实现视觉惯导融合定位。

本文设计实现的系统还可进一步完善，包括增加传感器的融合数量以及采集精度可以获得更高的精度，以及减少视觉丢失的情况。