轨道交通槽型梁结构振动噪声预测研究

左志远，秦佳良，朱 彬，韦 征，黄瑞堂，张用兵

（1.华东交通大学铁路环境振动与噪声教育部工程研究中心，江西 南昌330013；2.中铁第四勘察设计院集团有限公司，湖北 武汉430063；3.浙江省交通工程管理中心，浙江 杭州310009；4.中铁二十四局集团有限公司，上海200433；5.洛阳双瑞橡塑科技有限公司，河南 洛阳471003）

1 研究背景

随着我国经济的快速发展，为满足人们的出行需求，城市轨道的建设进入了蓬勃发展阶段。截止到2020年底，我国内地已有45座城市开通城市轨道交通线路7 969.7 km，位居世界第一[1]。目前城市轨道交通主要以地下线与高架线路为主，其中在高架线路中，由于槽形梁具有美观、施工便捷以及成本较低的优势，在国内外城市的轨道交通建设中得到了广泛的应用[2]。随着轨道交通的运量提升、速度加快，引发的轨道交通槽型梁低频振动与噪声问题越来越突出[3-4]。目前针对轨道交通桥梁振动与噪声产生及传播机理研究仍在不断深入，如何快速、精确预测轨道交通桥梁振动与噪声仍然是目前亟待解决的难题[5]。高飞等[6]听过了二维声场有限元模型预测桥梁结构噪声，并通过现场测试进行验证。LI等[7]通过结合有限元法与边界元法分析桥梁结构的噪声辐射特性。刘林芽等[8]通过结合有限元法与快速多极边界元法分析箱型桥梁结构的振动与噪声问题时，计算效率得以提高。目前针对桥梁低频振动与噪声的频域模型的研究相对较少。

本文基于动态柔度理论建立车辆-轨道-桥梁耦合动力学模型，采用ANSYS建立轨道-槽型梁有限元模型，采用LMS Virtual.Lab建立槽型梁边界元模型，结合以上三个模型进行联合仿真可以计算得到频域的车-轨-桥耦合动力响应与桥梁结构低频结构噪声，对槽型梁振动与噪声进行快速、精确的预测。

2 车辆-轨道-桥梁耦合系统频域分析模型

基于动态柔度理论建立车-轨-桥耦合频域分析模型，具体如图1所示。车辆采用10自由度多刚体模型，钢轨采用离散点支撑的Timoshenko梁，轨道板采用离散点支撑的两端自由Euler梁，桥梁采用简支Euler，扣件、CA砂浆层与支座均选用弹簧阻尼元件模拟[9]。

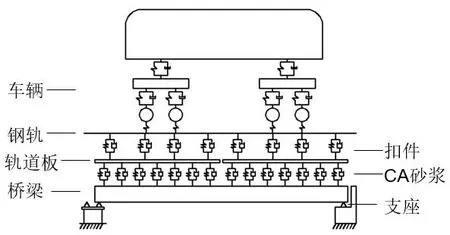
图1 车-轨-桥耦合动力学模型

单节车辆系统的柔度矩阵为：

式（1）中：Mv为车辆系统质量矩阵；Cv为阻尼矩阵；Kv为刚度矩阵。

轨道-桥梁系统位移矩阵[10]为：

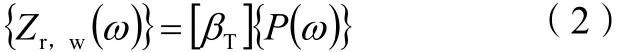
式（2）中：βT为轨道-桥梁系统动柔度；P（ω）为轮轨力。

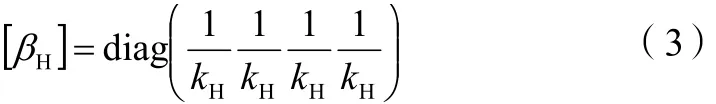
轮轨接触的柔度矩阵为：式（3）中：kH为轮轨接触刚度。

动态轮轨力计算公式为[11]：

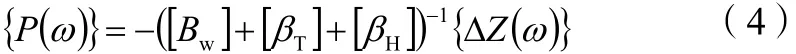
式（4）中：ΔZ(ω)为轮轨联合不平顺功率谱。

本文车辆选用地铁A型车，车速为80 km/h，通过计算轮轨垂向作用力，如图2所示。

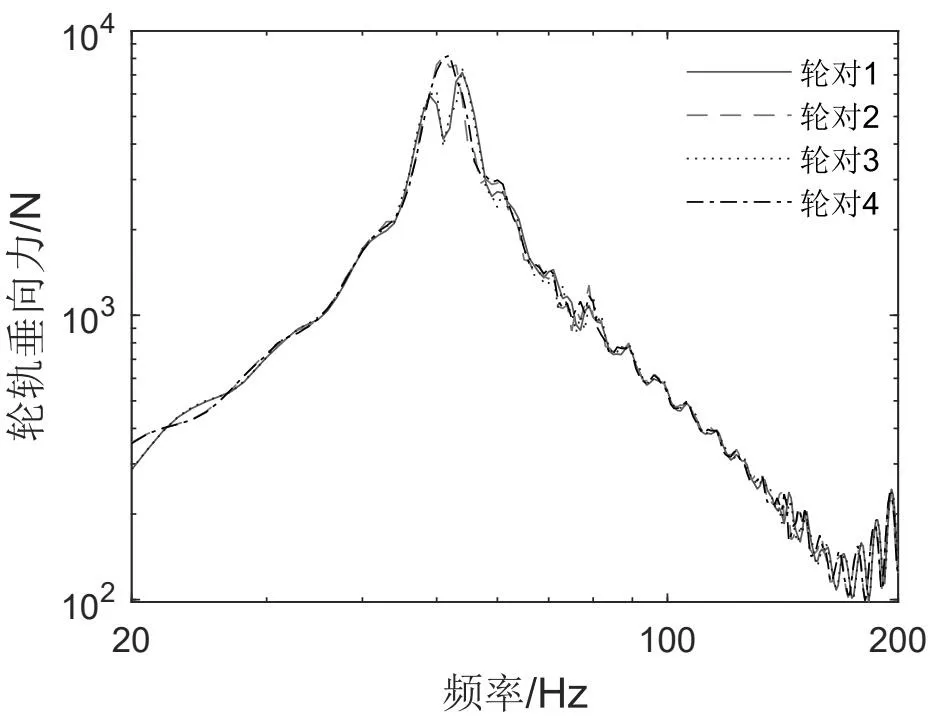
图2 轮轨垂向力

由图2可知，不同轮对对应的轮轨力基本一致，总体上看，优势频段控制在40～80 Hz，这是由于车-轨-桥耦合系统刚度所决定的。

3 槽型梁结构动力响应分析

3.1 有限元模型建立

利用ANYSY建立轨道-槽型梁有限元模型，采用标准跨径30 m，钢轨采用beam188单元，扣件采用combine14单元，桥梁采用solid185单元建立，所建模型如图3所示。

图3 轨道-槽形梁有限元模型

3.2 槽型梁振动响应分析

为了分析在动态轮轨力作用下槽型梁的振动响应，选取3个输出点，1～3号输出点分别为槽形梁跨中处左翼缘顶部中心位置、左腹板中心位置、底板线路中心位置，如图4所示。

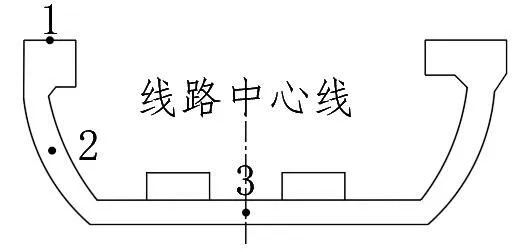
图4 各输出点布置情况

将轮轨力加载至钢轨上，计算得到槽型梁不同输出点的频域振动加速度响应，如图5所示。

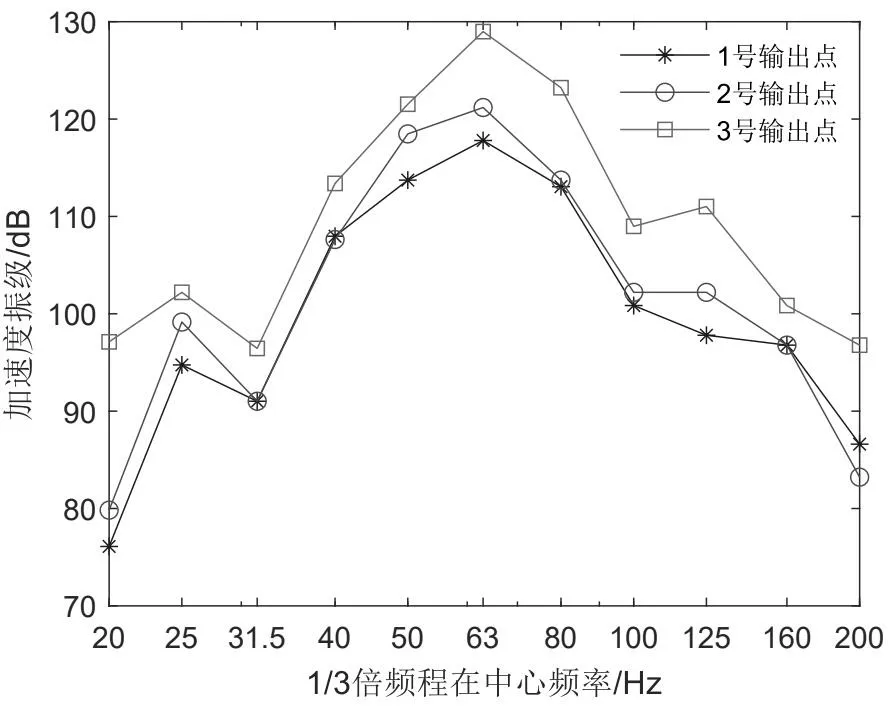
图5 各输出点频谱加速度

由图5可知，各输出点的加速度振级峰值频率均为63 Hz，且峰值频率处槽型梁各输出点振动加速度由大到小依次为：3号点>2号点>1号点，这是由于槽型梁底板直接受列车荷载的冲击作用，而腹板与翼缘的位置相对于底板距离荷载作用点较远。

4 槽型梁结构噪声预测分析

4.1 边界元模型建立

采用LMS Virtual.Lab建立槽型梁声学边界元模型，垂直于跨中一侧设置声场网格，尺寸为30 m×10.5 m，本节考虑地面反射，建立了半无限刚性地面，如图6所示。

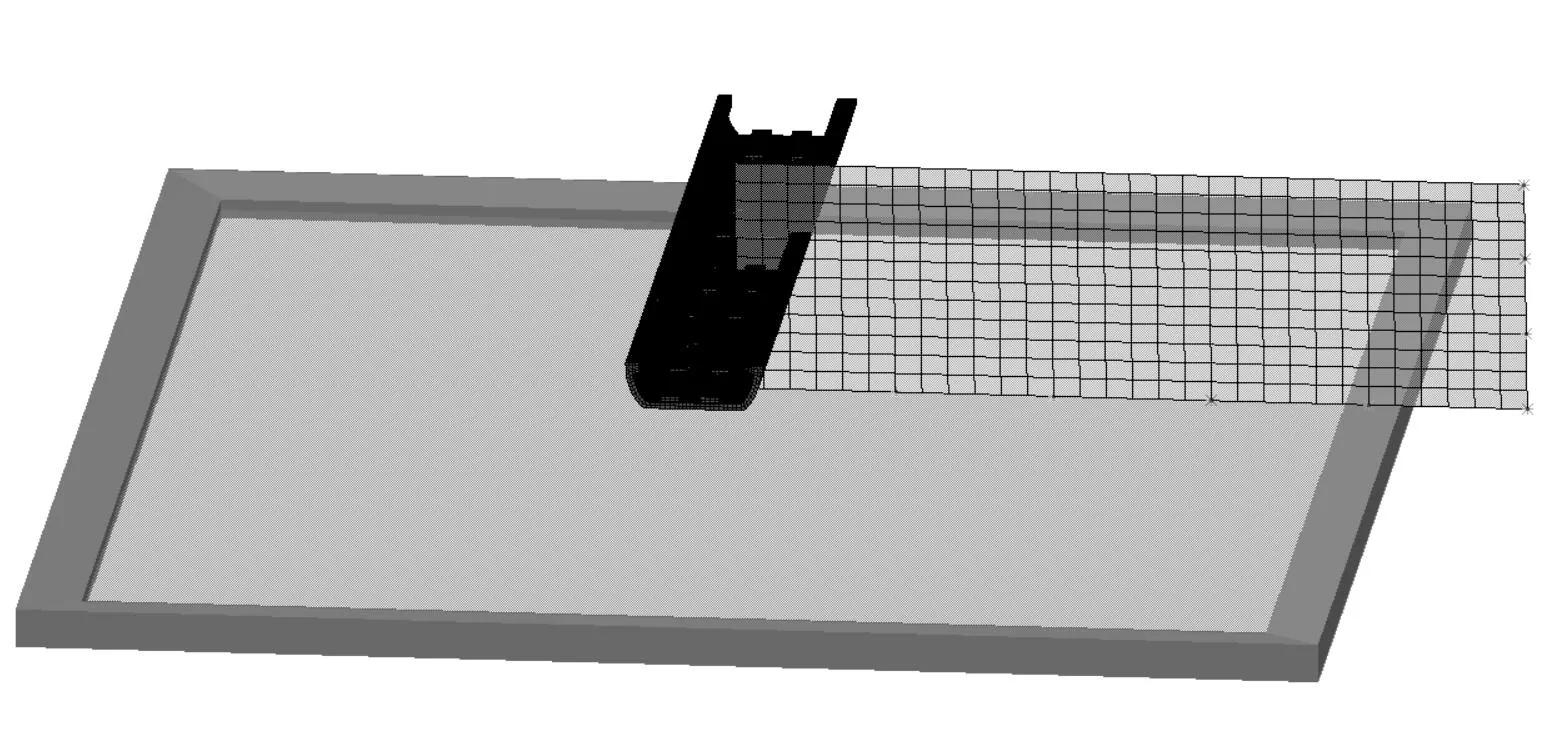
图6 槽形梁边界元模型

4.2 声学响应分析

为分析桥梁跨中声场特性，在梁底和梁右侧设置9个场点，场点1、2、3垂向设置在跨中梁底垂直于轨道中心线上，场点4、5、6沿声场网格向右侧设置在距离地面1.5 m处，场点4、5、6垂向设置于距离跨中30 m处的声场网格上，具体位置标点如图7所示。

图7 声场场点布置图

本文将9个声学场点分成3组进行对比分析，分别为1组：场点1、2、3，2组：场点4、5、6，3组：场点7、8、9。各声学场点1/3倍频程声压级曲线，如图8所示。

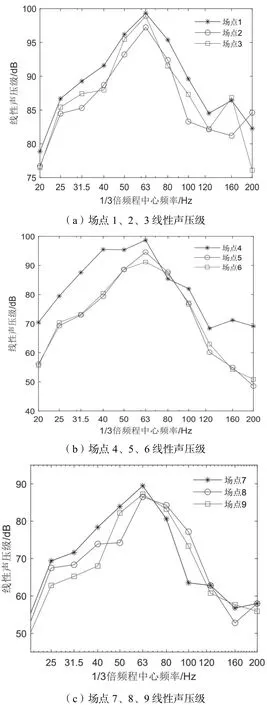
图8 各场点1/3倍频程线性声压频谱图

由图8可知，各场点声压级的优势频率均集中在40～80 Hz频段内，各场点的峰值频率均为63 Hz，规律与振动加速度响应一致。

由图8、9可知，场点1、2、3反映槽型梁跨中板底下方的声压竖向传递情况，且最大线性声压级排序为：场点1>场点3>场点2，这是由于刚性地面的声反射作用导致距离地面较近的场点3声压得到加强；场点4、5、6的最大线性声压级随着与槽型梁距离的增加而减小；场点7、8、9的最大线性声压级整体处于较低水平。

图9 各场点最大线性声压级

由以上分析可知，各场点线性声压级卓越频率均为63 Hz，本节通过计算该频率处槽形梁结构辐射噪声的声场分布情况，绘制声场分布图如图10所示。由图10可知，底板噪声辐射能力大于腹板，且传播范围更广、衰减速度较慢。

图10 声场分布图

5 结论

本文通过动态柔度思想建立车-轨-桥耦合垂向动力分析模型，采用ANSYS建立轨道-槽型梁有限元模型，采用LMS Virtual.Lab建立槽型梁边界元模型，基于以上三个模型进行联合仿真可以计算得到车-轨-桥耦合动力响应与桥梁结构低频结构噪声。得到结论如下：①由槽型梁振动加速度响应分析可知，各输出点的加速度振级峰值频率均为63 Hz，且底板振动加速度明显大于其他部位，这是由于槽型梁底板直接受列车荷载的冲击作用，而腹板与翼缘的位置相对于底板距离荷载作用点较远；②各场点声压级的优势频率均集中在40～80 Hz频段内，各场点的峰值频率均为63 Hz，规律与振动加速度响应一致；③底板下方垂向最大线性声压级出现先减小后增大的趋势，这是由于刚性地面的声反射作用导致距离地面较近的场点声压得到加强；④底板噪声辐射能力大于腹板，且传播范围更广、衰减速度较慢。