基于多服务器排队论的机械停车库最大泊位计算模型及仿真

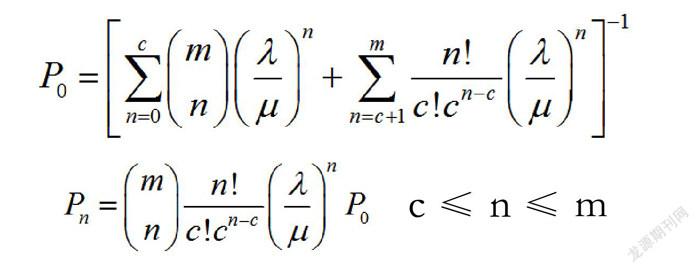
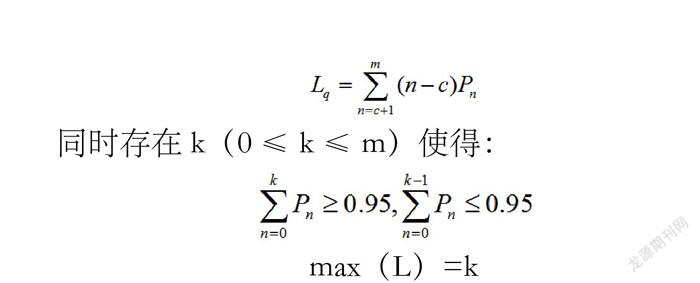
摘 要：随着城市用地资源的日益紧缺和机动车保有量的不断增加，机械式停车库的使用越来越频繁，随之带来的停车排队问题越发普遍。本文结合实际案例数据，根据多服务器排队论模型理论，建立测算机械式停车位的最大设计泊位的排队论模型，并对测算结果进行交通仿真，为机械式停车位设计提供理论依据和数据参考。

关键词：排队论;机械停车库;最大设计泊位;交通仿真

中图分类号：O226 文献标识码：A

0 引言

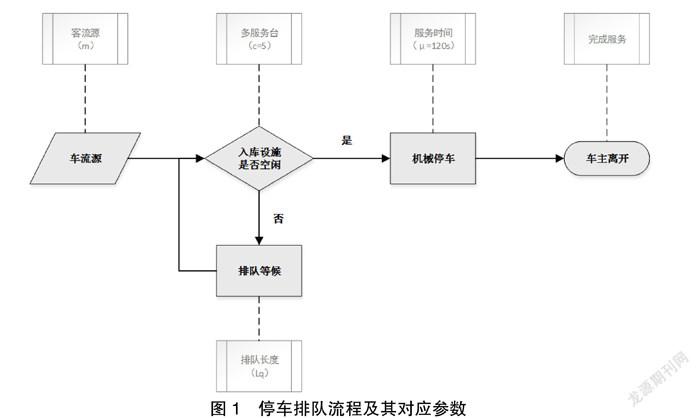
排队论（Queuing Theory）是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，又称随机服务系统理论。排队过程的一般表示：各个顾客从顾客源出发，随机地来到服务机构，按一定的排队规则等待服务，直到按一定的服务规则接受完服务后离开排队系统。

1 机械停车库停车问题的排队论模型

假设机械停车库排队停车问题为输入过程为泊松流，服务时间服从负指数分布的多服务台、有限等待空间的排队系统，即M/M/c/∞/m。

M/M表示早高峰车流到达规律服从泊松流，即越接近上班时间车流到达概率越大;停车时间服从负指数分布，即越接近平均服务时间概率越大;c=5为服务台个数，即机械停车库入口数;m为顾客总数。

以某办公总部大楼实际调查情况及各类技术指标确定模型参数，车辆于停车早高峰的1小时内全部到达，车辆按泊松流到达，平均间隔时间λ=m/60分钟;停车时间服从负指数分布，平均存取车时间≤100秒，最长存取车时间≤150秒，平均服務时间取μ=120秒。

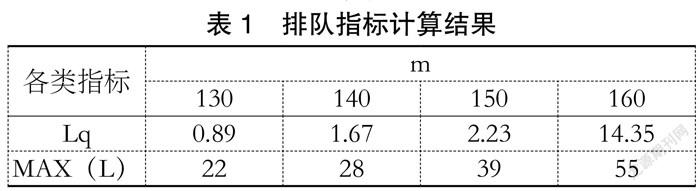
根据机械停车库的停车排队模型公式，利用matlab计算不同m取值下M/M/c/∞/m系统的平均排队长度Lq（平均车辆排队长度）、max（L）（最大排队长度），计算结果如表1。

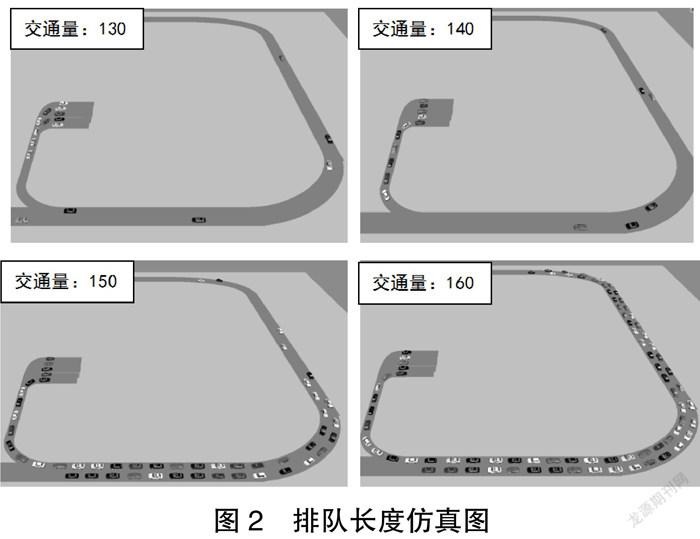
由计算经过可知，当开放130～140个车位时，最大排队长度增加相对平缓;当开放车位达到150个车位及以上时，最大排队队长度增速加快。因此，可知该机械式停车位开放的停车泊位应控制在150个车位以内。

2 交通仿真模型

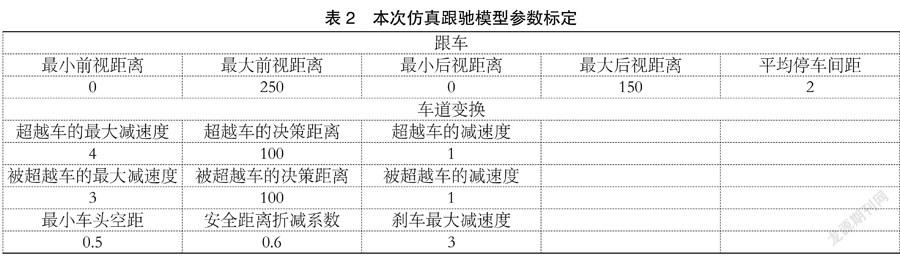
使用VISSIM建立Wiedemann交通模型。因此，为使得本次仿真车流运行效果能与真实交通情况尽可能地贴近，在参考相关资料，并对项目周边驾驶员基本驾驶行为进行调查后，修正了模型中的部分参数。主要参数：

依照本次现场的交通设施基础调查，以及对交通流量的构成与流量的调查，完成了对项目地块内部、外部的各种基础交通设施、通行数据进行了模型搭建。构成交通仿真模型。

机械停车库的出入口车道及停车库进口车道的排队长度如下表所示。

3 结论

本文结合实际案例数据，根据多服务器排队论模型理论，建立测算机械式停车位的最大设计泊位的排队论模型，并对测算结果进行交通仿真，根据实际案例数据，测算出机械式停车位的最大设计泊位数（150个），并通过Wiedemann交通模型对计算结果进行了仿真，验证了模型的准确度性和可行性，为机械式停车位设计提供理论依据和数据参考。

参考文献：

[1]胡建强，戴伟民.排队系统的泰勒展开方法[J].运筹学学报，2021（3）：147-159.

[2]刘煜飞，叶晴晴.基于矩阵分析方法的具有双阶段休假的排队系统驱动的流模型性能分析[J].数学的实践与认识，2021（4）：189-199.

[3]张恺琪，涂志莹，初佃辉，等.基于排队论的服务资源可用性相关研究综述[J].计算机科学，2021（1）：26-33.

[4]胡蓉，唐应辉.具有延迟休假和Min（N，V）-策略控制的M/G/1排队系统容量的优化设计与最优控制策略N*[J].数学的实践与认识，2020（19）：107-118.

[5]郝志香.基于排队论的旅游景点停车问题分析[J].当代旅游，2021（11）：35-36.

作者简介：夏雄（1986—），男，江西南昌人，工程硕士，研究方向：交通规划与管理、运输规划与管理。