卵石起动流速公式对比研究

摘要：卵石起动流速是泥沙起动流速的一种特殊形式。国内许多专家学者对于既适用于散粒体又适用于黏性细颗粒的泥沙起动流速公式进行过大量研究，究竟哪一种公式更适合卵石起动流速的计算与应用尚无定论。为了探寻这些公式的合理性与实用性，依托水工模型试验水深测试值和理论值，对于一些常用的公式进行了分析计算，又利用防沖槽冲坑深度反算卵石的起动流速，并且将试验计算值与理论计算值以及冲深反算值进行对比，间接地得出了长科院公式在卵石起动流速计算与应用方面更具有实用性的结论，以及该公式适用卵石粒径的范围。

关键词：卵石; 起动流速; 粒径范围; 水工模型试验

中图法分类号： TV142

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.11.033

0引 言

现代地貌形态取决于内、外营力的相互作用。内营力指构造作用所造成的地壳升降，从而构成侵蚀、堆积、环境变化的宏观地质背景;外营力指太阳辐射、降水及微生物活动等导致岩石风化、剥蚀及输移。由于侵蚀营力造成了水土流失，进而产生了泥沙。卵石是较大颗粒的泥沙，是一种特殊的表现形式。本文对于自然界分类的卵石、漂石、顽石一律采用卵石的通俗说法，即均称之为卵石（此处卵石粒径≥15 mm）。

众所周知，泥沙研究是水利专业学科研究的重要分支，其中的泥沙起动流速研究又是泥沙研究的主要内容。研究泥沙起动问题时，往往从泥沙起动流速入手[1]。早在200 多年前，就有人开始对泥沙起动流速进行研究。起动流速是研究河流泥沙运动规律的重要参量，也是泥沙研究的难题之一[2]。推移质运动是泥沙运动的一种重要形式[3]。而对于新疆众多的山溪性多泥沙河流上修建的引水渠首，在较大的卵石防沙、排沙以及利用其进行消能防冲方面，常常要对卵石这种推移质进行起动流速的研究和计算。卵石的起动有其特殊性，加强其起动流速及起动规律的研究，对工程泥沙及泥沙运动规律具有重要的价值。关于卵石起动较早的一些研究，都是按一般泥沙运动概念进行的。

一些研究以单颗粒泥沙的受力分析为出发点，考虑颗粒间黏结力，建立临界起动切应力或者起动流速公式[4]。较为典型的泥沙起动研究分为两个大的方面：“前苏联和中国”模式（以流速为主要参数）和“欧美”模式（以剪切力为主要参数）。20世纪30年代，Shields等分析了床面上泥沙颗粒的受力平衡，推导出无黏性均匀沙的起动切应力公式。Rouse根据Shields及他人的试验资料，绘测出著名的Shields曲线并推导出泥沙起动的拖曳力公式。此公式曾一度被欧美工程师用作判别泥沙初始运动的唯一准则[5]。还有学者通过研究得到了无黏性均匀沙的临界起动切应力公式[6]，也有研究认为只有沙粒切应力τ才对推移质泥沙运动起作用[7]。随后，又有学者提出公式τ1=γhJ′，根据Shields曲线，在颗粒雷诺数Re>500时，τc=0.06，而通过大量试验，得到无因次起动切应力τc=0.047;对于非均匀沙，有研究提出粗糙紊流中泥沙50%起动概率时相应的无因次起动切应力τc50=0.046，而根据实测资料都得到紊流中τc50=0.045;通过系统分析80 a来泥沙起动的研究成果和资料后得到，在沙卵石河流中，高雷诺数时，τc50在0.052～0.086之间，在低雷诺数时，τc50在0.030～0.073之间[8]。范玉通过研究表明对于散粒体粗颗粒泥沙，泥沙的起动拖曳力只与泥沙粒径有关，而和沙粒雷诺数无关[9]。

不过，基于流场和剪切力场之间的关系，更多的学者则是通过研究流速来判定泥沙的起动。中国在泥沙起动流速的理论研究上已达到了国际领先水平。目前仅针对非黏性泥沙提出的起动流速公式已超过100种[10]，其中窦国仁公式、张瑞瑾公式、唐存本公式、沙玉清公式等都有很大的影响。

张瑞瑾利用实测资料对系数与指数率定得到既适用于散粒体又适用于黏性细颗粒泥沙的统一起动流速公式，公式如下：

前3个公式虽然没有交代适用粒径范围，但都明确了可以应用于粗颗粒泥沙起动流速计算，公式（4）则是明确了适用于卵石起动流速计算。由此，本文依托水工模型试验水深测试值和理论值，对于这4个公式进行了分析计算，又利用防冲槽冲坑深度反算卵石的起动流速，并且将试验计算值进行对比，得出更适用于卵石起动流速计算的公式。

1模型设计和试验

1.1试验目的和内容

在具有一定泥沙组成的床面上，逐渐增加水流强度，直到使床面泥沙（简称床沙）由静止转入运动，这种现象称为泥沙的起动[12]。相应的临界水流条件称为泥沙的起动条件。泥沙的起动条件是泥沙的基本水力特性之一，同时，它又是河床冲刷的临界条件。确定泥沙起动的水力条件是泥沙运动力学的重要内容之一。吴彰松等[13]采用泥沙滚动起动模型开展了这方面的研究，刘蛟等[14]进行了三维水流作用下散列体泥沙的起动研究，李林林[15]也开展了卵砾石的起动研究，张根广等[16-17]研究了粗颗粒泥沙起动机理和斜坡上泥沙起动条件，毛宁[18]通过研究得到了块石起动流速公式，但以上研究与新疆多数修建于出山口较平缓开阔地带引水渠首的卵砾石起动规律有所不同。本文通过建立一个新疆山溪性多沙河流引水渠首闸后设置抛石防冲槽的标准断面模型，在施放3种不同流量、防冲槽中抛填6种不同粒径的卵石试验条件下，得出防冲槽正常的槽中水深试验值和理论值，为槽中卵石起动流速的计算提供基础参数。该模型试验主要用来研究防冲槽内水沙特性[19-20]，本次对于起动流速的分析只是采用了模型中的一部分试验数据，模型试验方案见表1。

1.2模型设计和制作

模型比尺为1∶30。

模型范围：以引水渠首闸后防冲槽为基准进行确定，设计为标准断面模型[21]，原型宽度27 m（见图1）。

1.3试验典型流量选取

全疆共有大小河流570条，其中年径流量0.74亿～2.39亿m3的河流有百余条，这些河流上修建的引水渠首泄洪单宽流量为8.21～17.52 m2/s，而且这些渠首有很多都采用了抛石防冲槽的防冲结构[22]。因此，结合试验场地条件，本次研究选取3个典型单宽流量（见表2）[23]，有其代表性与合理性。模型及试验如图2～5所示。

2流速计算与对比分析

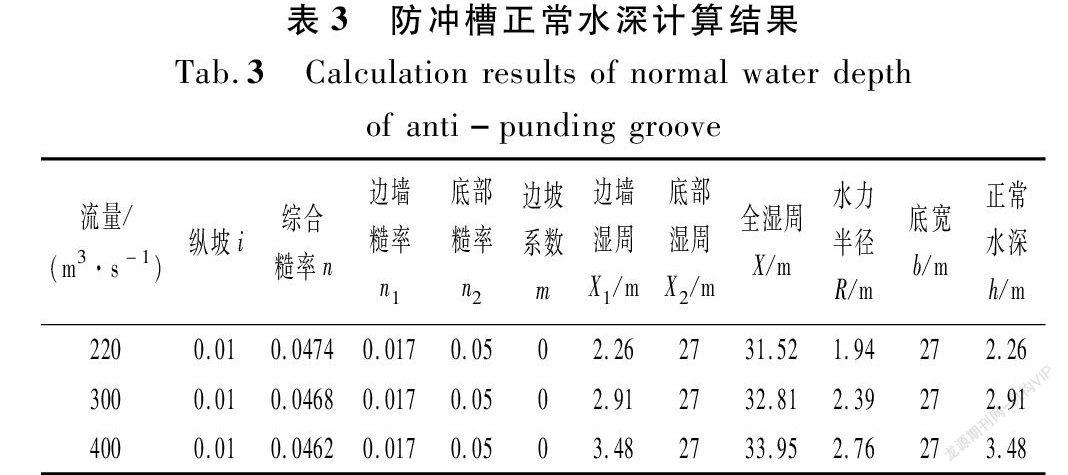
通过前述不同公式的表述可以看出，起动流速主要与正常水深、卵石粒径、容重、重力加速度、薄膜水厚度和孔隙率（这两个参数主要为沙玉清公式应用）等有关。本次没有通过试验直接去测试卵石的起动流速，而是通过与起动流速有关的水深和冲刷坑深来计算起动流速。起动流速应大于或等于某一个界限值，不冲流速应小于这个界限值，这两个界限值应是同一个数值，小于不冲流速，卵石就不会起动;大于或者等于起动流速，卵石就会起动从而造成冲刷。将试验测试的水深值代入前述不同公式得出起动流速试验计算值，又将防冲槽近似看作边墙现浇混凝土、底部堆砌均一卵石的渠槽，据此计算得到槽中正常水深，也代入前述公式得到一个起动流速理论计算值，再通过查阅相关不冲流速资料，在同等范围条件下，将起动流速与查询的不冲流速进行对比分析，对于起动流速与不冲流速接近的数值确定为可信值，从而得出最适用于卵石起动的起动流速公式。

2.1起动流速计算

2.1.1采用理论水深值的起动流速计算

防冲槽近似看作渠槽的理论水深值计算见表3。

2.1.2采用试验水深值的起动流速计算

通过抛填0.2～0.8 m不同粒径卵石，分别施放3种流量，采用长科院、张瑞瑾、沙玉清、岗恰洛夫公式进行起动流速计算。发现以下规律：① 长科院公式和张瑞瑾公式的试验值与理论值起动流速比较接近，反映出了理论与实际的一致性，沙玉清公式和岗恰洛夫公式在理论与实际的一致性方面偏差较大;② 各抛石粒径下，卵石起动流速与施放流量关系不大，随着抛石粒径的增大，卵石起动流速也随之增大;③ 抛填0.2～0.6 m卵石，各种工况条件下，随着抛石粒径的增大，卵石起动流速也随之增大，但是抛填0.8 m卵石条件下，起动流速呈现明显降低现象。计算统计结果见表4。

2.1.3采用试验冲刷坑深反算起动流速

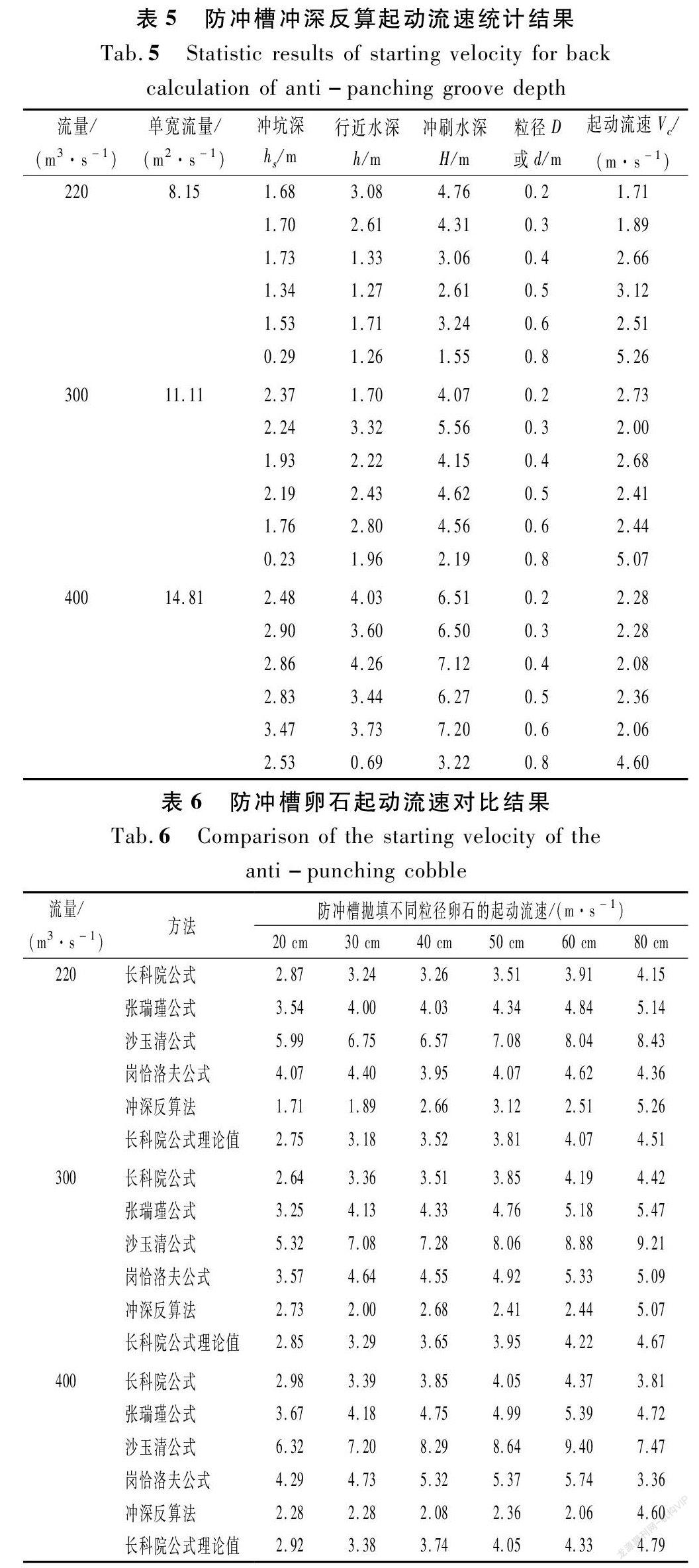
防冲槽冲坑最深处可认为是冲刷最剧烈的位置，试验中分别测出了冲刷坑处的冲刷水深h（含冲坑深）。根据冲刷极限状态法，有Q=BhU;另外，河床抗冲粗化层的计算可以通过水流连续公式q=Uh来计算。此两式中Q为流量，B为宽度，h为冲刷达到极限状态的水深即为冲刷水深，U为起动流速，q=Q/B。因此，单宽流量q与冲刷水深h的比值即为起动流速U。采用防冲槽冲坑试验值反算的起动流速统计见表5。

从表5可以看出，在同一流量下，随着卵石粒径的增大，冲深反算值起动流速总体呈现出上升趋势，反映出了试验的客观规律;由于试验过程中冲坑深与水深测量总会存在一些人为因素造成的误差，使得该冲深反算值产生了异常的波动趋势，但就数值而言，还是有一定可靠度的。

2.2对比分析

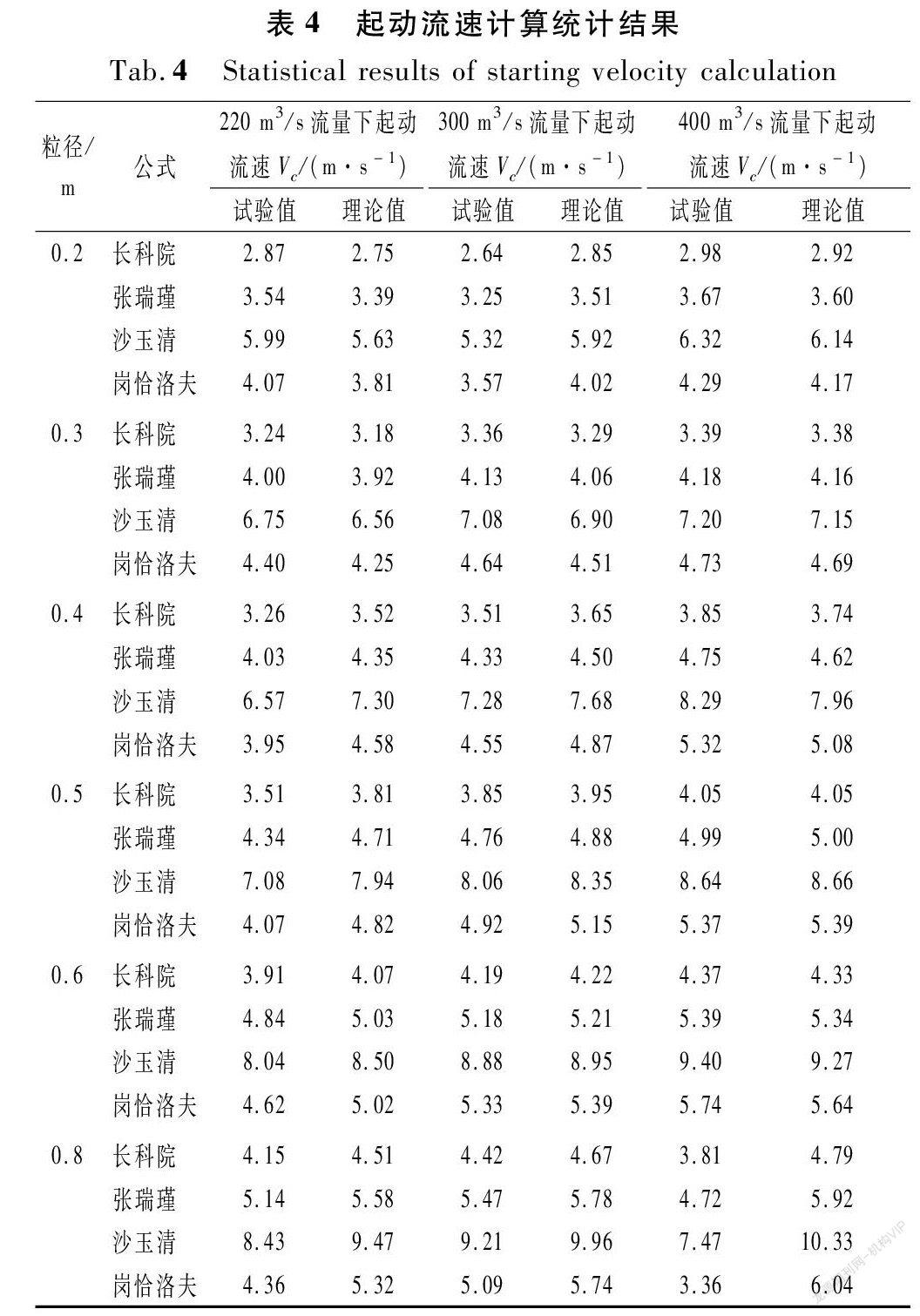
将起动流速的上述计算结果进行对比分析，发现冲深反算值最小;其次是长科院公式的试验计算值和理论计算值（这两个值比较接近），吻合程度最高;根据前述沙玉清公式和岗恰洛夫公式得到的试验计算值与卵石起动流速吻合程度最差，张瑞瑾公式计算值相比长科院公式值较高，高出长科院公式值0.67～1.13 m。这也反映出现有公式在渗流作用明显处，计算泥沙起动流速时，会大于实际起动流速[24]。将4个公式的试验计算值、长科院公式理论计算值与冲深反算值放在一起进行对比（见表6）。

为了更清晰地对比，按照不同流量将表6中数值分别绘图分析，如图6所示。

防冲槽可近似看作渠槽，渠底卵石一般是松散堆积的，按照有关规范，可当作非平面形卵石、砌筑来考虑，对于水力半径等于2，粒径为200，250，300 mm时，不冲流速分别为3.0，3.5，3.7 m/s[25];还有规范规定，干砌卵石渠道允许不冲流速为2.5～4 m/s[26]。从试验数据来看，当流量为220 m3/s，卵石粒径由200 mm逐渐增大至800 mm时，冲刷断面处的最大流速由3.21 m/s逐渐增大至5.58 m/s;当流量为300 m3/s，卵石粒径由200 mm逐渐增大至800 mm时，冲刷断面处的最大流速由4.16 m/s逐渐增大至8.15 m/s;当流量为400 m3/s，卵石粒径由200 mm逐渐增大至800 mm时，冲刷断面处的最大流速由4.44 m/s逐漸增大至9.52 m/s。这些流速值是已经发生冲刷时的数据，而起动流速肯定会比冲刷时的流速值小很多才可能造成之后较大的冲刷。沙玉清公式明显数值偏大，岗恰洛夫公式在本次试验中最大流量、最大卵石粒径条件下数值反而下降很多，且多数数值基本大于冲深反算值的1.5～2倍，与现行规范也不相符，不适用于此类卵石起动流速计算;张瑞瑾公式数值基本大于冲深反算值的1.0～2.6倍，而且200，300 mm粒径的流速值也不满足现行规范的要求，也不是理想的公式;只有长科院公式试验计算值与理论计算值较为接近，不但满足现行规范的要求，而且除了800 mm粒径外，冲坑深反算值均小于长科院公式值，并且也发现卵石粒径为800 mm时，试验值规律性、代表性不强。

该试验属于引水枢纽下游泥沙冲刷的水力学研究范畴，虽然与河流动力学研究范畴有所差异，但是下游泥沙冲刷与抛石的起动流速有着直接的关系，也就因此与河流动力学范畴有了紧密联系，而且防冲槽内抛石的起动与冲刷比之天然河道卵石起动情况要复杂的多，水流条件也剧烈很多，开展此项研究具有一定意义。通过上述分析可以初步认为：长科院公式适用于卵石粒径d≤600 mm的起动流速计算，d>600 mm粒径卵石的起动流速计算还需要去除颗粒之间黏结力等因素开展进一步研究。

3結 论

（1） 经过验证，文中提到的可用于散粒体或粗颗粒泥沙、卵石起动流速的4个经验公式中，长科院公式理论值与实际值接近，用于卵石起动流速计算最为可靠和实用。

（2） 卵石起动流速应大于或等于界限值，卵石不冲流速应小于界限值，这两个界限值应是同一个数值;小于不冲流速，卵石就不会起动;大于或者等于起动流速，卵石就会起动从而造成冲刷。

（3）长科院公式适用于卵石粒径d≤600 mm的起动流速计算。

参考文献：

[1]蔡蓉蓉，张罗号，张红武.李保如泥沙起动流速公式修正研究[J].水利学报，2019，50（5）：547-554.

[2]马志敏，邹先坚，赵小红，等.基于B超成像的泥沙起动流速测量方法[J].水科学进展，2015，26（1）：59-59.

[3]吕升奇，郭美娇，袁礼伟.淹没柔性植物对明渠推移质运动影响的实验研究[J].人民长江，2016，47（2）：67-71.

[4]刘洁，刘洁玉，白玉川.黏性泥沙流变特性及其临界起动的研究[J].泥沙研究，2015（6）：59-64.

[5]闫红杰，史雅君，周萍，等.河床泥沙起动流速公式修正及可靠性验证[J].科学技术与工程，2018，18（17）：297-301.

[6]李林林，张根广.渗流作用下岸坡泥沙起动流速研究[J].人民长江，2017，48（23）：84-88.

[7]黄才安，奚斌.推移质输沙率公式的统一形式[J].水利水运科学研究，2000（2）：72-78.

[8]汤洁.壅水条件下水流结构及床面泥沙起动研究[D].武汉：长江科学院，2016.

[9]范玉.水沙两相流理论及引水工程管道输沙问题的研究[D].天津：天津大学，2014.

[10]朱正雷，邵宇阳，赵晓晴.基于FLUENT的便携式泥沙起动测量装置模拟效率与精度[J].水电能源科学，2019，37（6）：156-156.

[11]水利部水利水电规划设计总院.堤防工程设计规范：GB 50286-2013[S].北京：中国计划出版社，2013.

[12]周双，谢飞，李福育，等.负坡上均匀散粒体泥沙起动流速研究[J].中国水运，2016，16（12）：225-225.

[13]吴彰松，张根广，寇潭，等.基于概率统计理论的泥沙起动流速研究[J].长江科学院院报，2017，34（7）：7-11.

[14]刘蛟，严军，刘铁，等.三维水流作用下散列体泥沙的起动研究[J].泥沙研究，2015（1）：7-13.

[15]李林林.基于统计理论的推移质起动概率及输移规律[D].杨凌：西北农林科技大学，2018.

[16]张根广，周双，邢茹，等.基于相对暴露度的无黏性均匀泥沙起动流速公式[J].应用基础与工程科学学报，2016，24（4）：687-697.

[17]张根广，王新雷，吴彰松，等.泄水建筑物下游冲刷坑二维数值模拟[J].泥沙研究，2017，42（3）：42-47.

[18]毛宁.论泥沙砾石的起动流速[J].长江科学院院报，2011，28（1）：6-11.

[19]李江峰，尹辉，耿凡坤，等.抛填不同粒径卵石对闸后防冲槽的影响研究水工模型试验研究报告[R].乌鲁木齐：新疆水利水电科学研究院，2018.

[20]李江峰，李娟，尹辉，等.基于标准断面的防冲槽水沙特性研究水工模型试验研究报告[R].乌鲁木齐：新疆水利水电科学研究院，2019.

[21]李江峰，尹辉，戚印鑫，等.抛石粒径对防冲槽结构和冲刷的影响研究[J].水利与建筑工程学报，2019，17（3）：115-120.

[22]戚印鑫，张磊，孙娟，等.白杨河阿克苏渠首除险加固工程可行性研究报告[R].乌鲁木齐：新疆水利水电科学研究院，2018.

[23]李江峰，尹辉，戚印鑫，等.渠首闸后防冲槽的抛石粒径与消能试验研究[J].水利与建筑工程学报，2019，17（6）：117-181.

[24]闫红杰，史雅君，周萍，等.河床泥沙起动流速公式修正及可靠性验证[J].科学技术与工程，2018，18（17）：297-301.

[25]中华人民共和国水利部.渠道防渗工程技术规范：GB/T 50600-2010[S].北京：中国计划出版社，2011.

[26]中华人民共和国水利部.灌溉与排水工程设计标准：GB 50288-2018[S].北京：中国计划出版社，2018.

（编辑：谢玲娴）

Abstract：Pebble starting velocity is a special form of sediment starting velocity.Many experts and scholars have conducted a large number of studies on the starting velocity formula which is applicable to both loose particles and viscous fine particles，but there is still no final conclusion on which formula is more suitable for the pebble starting velocity.In order to explore the rationality and practicability of these formulas，we relied on the water depth test values of hydraulic model test and theoretical value to analyze and calculate some commonly used formulas，and used the anti-flushing groove depth to inversely deduce the starting velocity of the pebble.Then we compared the experimental calculation values，theoretical calculation values and the inversed deduced values of the scouring depth.The results showed that the formula of Changjiang River Scientific Research Institute was more practical in the calculation and application of the pebble starting velocity，and the range of the particle size of the pebble applicable to the formula was obtained.

Key words：pebble;starting velocity;range of the particle size;hydraulic model test