基于PCHD模型的LCL型APF自适应模糊无源控制策略
吉晓帆,张代润,周驭涛,黄伟,陶聪
(四川大学电气工程学院,四川 成都 610065)
电力系统中的谐波由于大量电力电子设备等非线性负载的使用而急剧增多。大量未经处理的谐波电流汇入电力系统中不仅会降低电能生产、传输、使用的效率,同时也会影响一些高精尖等谐波含量要求较高的用电设备的正常工作[1]。为此,如何有效治理谐波问题引发了众多学者的广泛关注。
传统的无源电力滤波器(passive power filter,PPF)只能滤除特定频率的谐波,并且滤波效果对电路参数敏感。有源电力滤波器(APF)作为一种抑制谐波的电力电子设备,能同时对多个不同频率谐波进行灵活补偿[2],且补偿效果具有对电路参数不敏感、动态响应速度较快等特性[3]。
目前,已有多名学者将不同的控制算法和优化思路用于有源电力滤波器,并取得了较好的效果。文献[4]为改善APF的动态性能,采用“重复控制+滞后一拍”的PI控制跟踪参考电流,并利用蝙蝠算法优化参数。文献[5]为了充分补偿3次谐波,利用PR改进了电流控制器,并采用LCL滤波器和SDFT谐波检测法。文献[6]将滑模变结构引入滞环矢量控制,以期提高APF遇到未知扰动或运行状态变化时的系统响应速度。文献[7]对LCL型单相APF进行了研究,提出一种重复H∞控制策略,其仿真表明该控制具有良好的鲁棒性。文献[8]提出了一种简化预测寻优的APF控制方法,以减少双矢量预测控制算法的复杂度。文献[9]提出了基于参数在线调整的新型广义积分以减少系统的稳态误差,并用滑模控制抑制系统的LCL滤波器谐振问题。文献[10]提出了模糊神经网络全面滑模控制,实现了全局鲁棒性,并且提高了动态响应能力。文献[11]将免疫反馈控制与重复控制结合用于控制APF,并在其中引入粒子群算法对重复控制参数寻优,其抑制谐波和补偿无功效果明显。
为了提高对谐波检测的快速性和APF补偿谐波的能力,本文基于LCL型两电平变流器的无源性,首先建立了LCL型并联APF的端口受控的耗散哈密尔顿(PCHD)模型,其次介绍了正弦幅值积分器(sine amplitude integrator,SAI)检测基波的原理,并且设计了LCL型APF的无源控制器,在此基础上设计了模糊控制来实时在线调节参数,以提高APF系统直流侧电压的稳定性,保证系统的动态、静态性能。仿真结果验证了所提出控制策略的可行性和有效性。
1 LCL型APF的PCHD模型
三相并联型APF系统采用的是两电平变流器并带有LCL型滤波,如图1所示。其中,usa,usb,usc为网侧的三相交流电压;ua,ub,uc为变流器输出的三相电压;isa,isb,isc为电网侧的输出电流;i2a,i2b,i2c为网侧电感的输出电流;iLa,iLb,iLc为非线性负载的输入电流;L1,L2和C构成了APF的滤波器,其中R1和R2分别是L1和L2的等效电阻;udc,Cdc分别为APF直流侧电压和电容。

图1 LCL型APF拓扑结构Fig.1 Topology of LCL type APF
LCL型两电平变流器的数学模型在很多文献中[12]都有介绍,这里不再详细推导。直接给出其d,q轴下数学模型,如下式所示:

式中:Sd,Sq,i1d,i1q,i2d,i2q,uCd,uCq,usd,usq分别为开关函数S,i1,i2,uC,us在d,q轴上的分量;ω为电网角频率。
一般地,选取储能元件相应代表储能的量作为状态变量。因此本文选取APF系统的状态变量为

建立代表系统各电感电容能量之和的Hamilton函数如下式:

一般地,变流器系统的PCHD模型可表示为
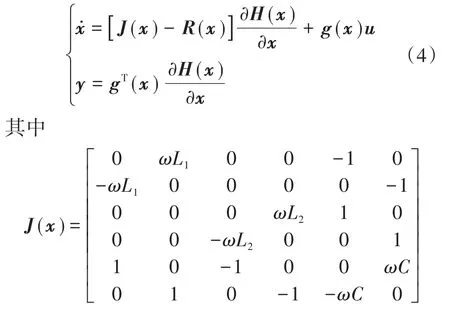

式中:J(x)为表征系统的内部结构的矩阵;R(x)为反映系统的耗散的半正定对称矩阵;g(x)为体现系统的内外部关联的矩阵。
将式(1)转化为式(4)形式,可以得到APF的PCHD模型。

式中:x,u分别为系统状态变量和系统输入。
由式(5)可知系统满足无源条件[13],且具有严格无源性,可进行无源控制器设计。
2 正弦幅值积分器
为了实现对正弦型信号的无静差跟踪,可以采用对正弦信号进行积分,通常只需用到幅值,所以用正弦幅值积分器来进行跟踪正弦信号。其传递函数为[14]

式中:ω0为SAI的中心频率。
由于只需得到基频电流,因此中心频率取为ω0=100 rad/s。SAI传递函数的Bode图如图2所示。可以看出,SAI相当于一个带通滤波器,对中心频率ω0处进行幅值谐振,而在其他频率处均为幅值衰减[15]。
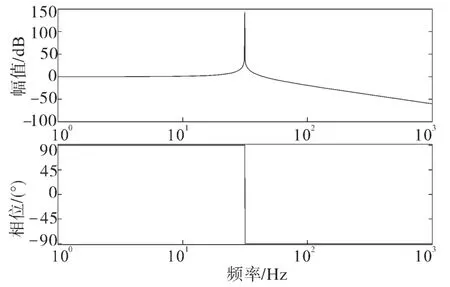
图2 SAI的Bode图Fig.2 Bode diagram of SAI
同时,由于SAI传递函数中复数j的存在,可以利用α,β轴上的一对正交信号实现。假设输入信号为 iα=cos(ω0t),iβ=sin(ω0t),经过 SAI输出为iα1,iβ1,可以表示如下:

由于输入信号的正交性,可得 Uα1=-jUβ1,对式(7)进行交叉解耦可得:

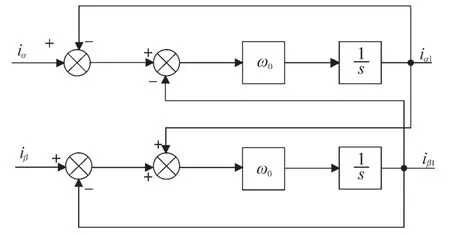
图3 SAI实现框图Fig.3 Block diagram of SAI
3 LCL型APF无源控制器设计
如果已知一个无源系统,系统能量的耗散性会使注入的能量和阻尼重新分配,并使系统总能量收敛到期望能量,且能量相对应的状态变量收敛到期望平衡点。工程中为了减少采用PCHD模型控制器复杂度,常用互联阻尼配置无源控制(interconnection and damping assignment passivitybased control,IDA-PBC)方法进行注入能量和阻尼来设计无源控制器,使无源控制器具有较快的收敛和轨迹可控。
为实现跟踪谐波电流并使网侧功率因数单位化,则期望平衡点为

假设能找到Ja,Ra和矢量k(x)=∂Ha(x)/∂x,满足下式:

式中:Jd(x),Rd(x),Hd(x)分别为注入能量后的互联矩阵、耗散矩阵以及总能量矩阵。
令

且k(x)满足可积性:

在平衡点处取得极值:
本文所涉及的工程建设活动中,在招投标工作中所存在的主要问题,虽然是个别地方、企业的现象,但在行业内影响极坏,不利于我国的经济建设和社会稳定,希望各级政府、地方建设行政主管部门应加大执法力度,完善法律法规及相关规章制度,把工程建设活动中的招投标工作纳入法制化轨道,真正实现通过引入竞争,达到降低工程造价,确保工程质量的目的。

Lyapunov稳定性有:

IDA-PBC的控制思想是确定一个控制规律,使无源系统的闭环PCHD模型为

则由式(10)~式(15)得到无源控制器控制规律u如下式:
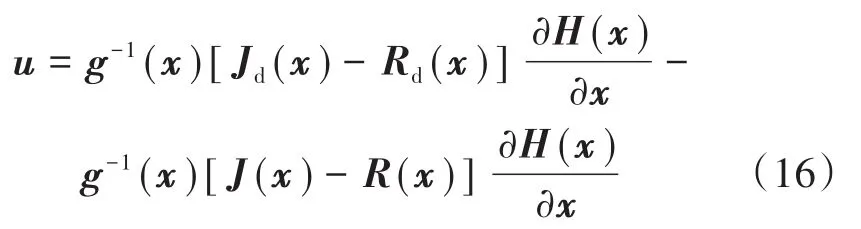
当控制器参数Ja,Ra,k(x)不同时,系统的收敛速度和性能均有差异,因此本文设计采用互联和阻尼注入的控制方式[11],取性能较好Ja=0,Ra=0的方案,即

可将式(10)转化为
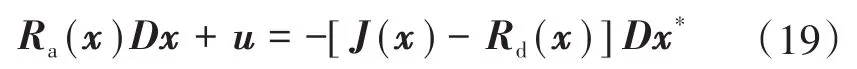
将式(19)展开,得:

可得控制器方程可得到系统的开关函数为

综上,由于系统是严格耗散系统,并且由能量函数Hd的形式可知其为连续可微正定函数,所以直接选取Hd作为Lyapunov函数进行稳定性分析。求得Hd(x)的一阶导数为
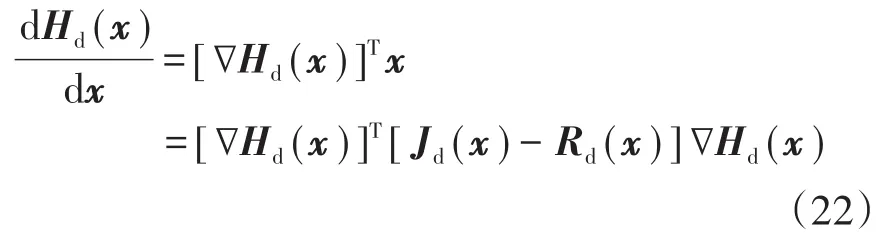
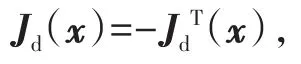

又由Rd(x)是半正定矩阵,从而得知Hd(x)恒为非正数,即Hd(x)是半负定的,且只有在x→x*时等于零。
由以上分析可知系统在新的平衡位置渐进稳定。
4 直流侧模糊控制


图4 直流侧模糊控制原理图Fig.4 Fuzzy control schematic diagram of DC side


表1 模糊控制规则表Tab.1 Fuzzy rules table for e and ec
综上所述,LCL型APF的整体控制策略框图如图5所示。

图5 模糊自适库无源控制整体控制框图Fig.5 Fuzzy adaptive passive control block diagram
5 仿真算例
为了验证本文设计的无源控制的LCL型APF具有的可行性和补偿电流的有效性,在Mat⁃lab中搭建仿真模型,并对不同仿真算例的结果进行分析。其中,电网为三相平衡正弦电源,幅值为380 V;非线性负载为三相不可控整流桥,其负载侧电阻为4 Ω;考虑裕量及电容容量,udc大于2倍线电压有效值,本文选取800 V。其他仿真参数为:直流侧电压udc=800 V,开关频率f=10 kHz,滤波电感内阻R=0.1 Ω,滤波电感L1=5 mH,滤波电感内阻R1=0.1 Ω,滤波电感L2=5 mH,滤波电感内阻R2=0.1 Ω,滤波电容C=10 μF,额定电压角频率ω=100π rad/s,直流侧电容Cdc=2 200 μF,预设比例系数Kp=2.27,预设积分系数Ki=50。
算例1:为了验证前文所提的SAI谐波检测算法的快速性,与ip-iq法进行对比。图6为检测的基波波形,其中,图6a为ip-iq法检测的基波波形,图6b为SAI法检测的基波波形。从图中可以看出,基于SAI的谐波检测方法可在1个工频周期内稳定检测到基波,而ip-iq法则在2个工频周期才稳定检测到基波分量。由此可说明,SAI法较ip-iq法有明显的速度优势,由前述原理可知,这是由于SAI法没有用到具有延迟的低通滤波器。

图6 不同算法检测的基波波廝Fig.6 Fundamental waveforms detected by different algorithms
算例2:由于算例1已经检验了SAI检测谐波的可行性,所以在本算例中,直接应用该检测算法,并同时验证动、静态时所提控制策略的有效性和可行性。由于三相对称,所以分析时,只取a相波形。图7a、图7b分别为APF输出的电流波形和APF参考电流波形。从图中可看出,在本文所提的控制策略下,APF输出电流跟踪谐波电流速度较快,且两者波形相近,跟踪误差较小。

图7 输出电流与参考电流对比Fig.7 Comparison between output current and reference current
图8为无源控制补偿后的波形图。其中,图8a为非线性负载的a相电流,可看出非线性负载的波形已经明显不是正弦波,且含有较多成分的谐波;补偿后的电网电流和直流侧的电压波形如图8b、图8c所示,由波形可以看出,直流侧的电压波形在开始时由额定值800 V下降约20 V,占电压幅值的2.5%,但是较快恢复到额定值800 V,并有小幅度波动。这表明直流侧电压控制效果良好,电网侧波形在1个工频周期后稳定,波形正弦度较好。
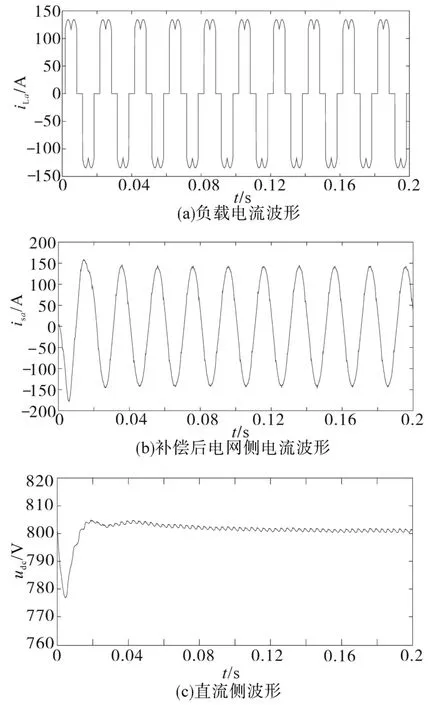
图8 无源控制补偿后的波廝图Fig.8 Waveforms using passive control strategy
图9、图10分别为补偿前、后网侧电感输出的a相电流及其频谱分析。由图9的FFT分析可知THD为30.84%;由图10的谐波分析可知THD为2.42%,较补偿前下降了92.2%。补偿谐波效果说明了稳态时无源控制策略的有效性。
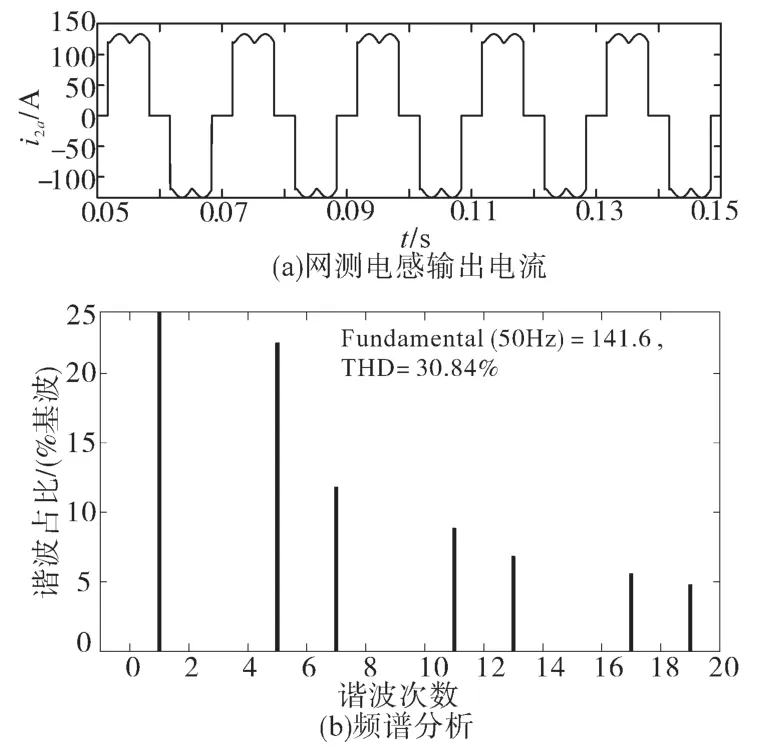
图9 不采用无源控制策略的网侧电感a相电流输出及其频谱分析Fig.9 Phase a current output by grid side inductance and its spectrum analysis without using passive control strategy

图10 采用无源控制策略的网侧电感a相电流输出及其频谱分析Fig.10 Phase a current output by grid side inductance and its spectrum analysis using passive control strategy
为了验证负载突变时,本文控制策略仍然有效,进行负载突变试验。在0.15 s时突加1倍负载,并在0.5 s时切除突加的1倍负载,结果如图11所示。从图11可知,突加负载时刻,非线性负载电流迅速变为原来的2倍后稳定,在切除负载时刻,负载电流迅速恢复。补偿后电网侧电流波形在突加负载时刻迅速变为原来的2倍并稳定下来,切除时刻电网电流迅速恢复为突加负载前的电流幅值。并且由直流侧电压可知,突加负载时,电压经历短暂下降,约20 V,恢复原有负载时,电压短暂超调约20 V。以上说明,本文策略在负载突变时具有较快的动态响应,且鲁棒性较强。
6 结论
本文所提出的基于LCL型APF的无源控制策略,利用SAI结构简单、运算简便的优点,提高了检测谐波的速度,同时基于LCL型APF的数学模型,构建了PCHD模型,进行了无源控制器设计,证明了控制器在平衡点处具有渐进稳定性。此外,设计了直流侧模糊PI控制,仿真结果显示直流侧电压最大下降为参考值的2.5%,表明其稳定直流侧电压的效果良好。APF稳定运行时,电网电流畸变率THD由30.84%下降至2.42%。表明所提策略能有效抑制电流谐波。负载突变时,补偿效果和直流侧电压稳定性仍能得到保证,表明模糊PI控制和无源控制器具有较强的鲁棒性和抗扰能力。仿真结果证明了本文所提无源控制策略的有效性。

