基于轨迹大数据的动态最优路径规划

张小芳，冯慧芳

(西北师范大学数学与统计学院，甘肃 兰州 730070)

0 引 言

社会车辆数量过多、区域间物资分配差异过大以及道路容量不足或设计不妥导致城市交通拥堵问题日渐严重，这些问题不仅降低了乘客的出行体验，增加了出行成本，还引发了环境污染、交通安全等一系列问题。这些问题已经难以由传统的交通管制、限号等措施解决。

随着智能交通系统(ITS)的崛起，这个难题有了突破性的进展。ITS能够有效地利用现有交通设施，实现人、车和路的有机结合和协调发展，优化城市交通网络，提高运输效率，降低环境污染等。最优路径规划是智能交通系统、智能车载导航系统中的关键内容，近年来受到城市交通、地理信息系统、计算机科学等领域的国内外学者的广泛关注。通过合理的路径规划，不仅能使人们的出行更高效、快捷，同时也能缓解交通压力，有助于交通管理和控制。传统的最短路径规划算法[1-2]主要包括Dijkstra算法、遗传算法、蚁群算法、Floyd算法以及神经网络算法等。这些传统方法虽然在一定程度上满足了一定需求的路径规划，但由于城市交通网络比较复杂，以及许多交通约束的存在，这些方法仍不能解决真实交通网络中的路径规划问题，因此很多学者对这些方法进行了改进。

Fan等人[3]对经典Dijkstra算法进行了研究，通过改进其数据存储结构和受限算法的搜索范围来提高算法的有效性。吴红波等人[4]将路况信息与道路风险作为影响因素对Dijkstra算法进行了改进，建立车辆行驶路线选择模型，并借助GIS网络分析技术对最优路线进行分析与验证。Wei等人[5]用改进的Dijkstra算法来解决最大负载路径问题。Guo等人[6]考虑车辆油耗和排放测量因素，以最短时间、最短距离、最少燃料消耗和最低排放等为优化目标改进了Dijkstra算法，最后使用ArcGIS和MATLAB软件对该算法进行了仿真验证。Huang等人[7]引入路径的权值矩阵，增加基于角度因子函数和可见性函数的转移概率函数，设置惩罚函数以提高路线搜索的准确性。马荣贵等人[8]通过重新定义启发函数和信息素更新算子来改进基本蚁群算法，提出了一种多约束质量最优路径算法。文献[9]提出了一种改进的离散蝙蝠算法(IDBA)。该算法首先利用Floyd-Warshall算法将不完全连通图转换为完备图，然后模拟蝙蝠的觅食和避障过程，在完整图中寻找满足约束条件的最短路径。

在真实的城市交通网络中，两点间的路程最短路径可能由于拥堵等客观因素使得行驶时间变长，即不一定是最优路径，因此，有必要进行动态最优路径规划。此时，交通大数据的迅速发展吸引了研究者们的注意力，成为城市交通路径规划研究的一种新途径。交通大数据内容丰富，通过数据挖掘技术就可获得城市交通网络的动态性特征，为进一步的交通路径规划做准备。

Zhang等人[10]使用一种改进的基于概率的路径选择算法构建了一张道路图，然后使用SPFA在构建的道路图上进行最优路径规划，但仅考虑了道路长度这个单一因素。Zhao等人[11]构建多层次路网结构，通过挖掘大量出租车轨迹获得路网各个路段的属性，然后使用Floyd算法为出租车驾驶员提供最快行驶路径。Yan等人[12]将用户偏好与实时交通条件相结合，建立了一种动态实时路径选择模型，通过自适应学习算法为车辆提供更加准确和个性化的路径选择策略，实验结果表明该模型有效地减少了车辆的平均行驶时间。文献[13]将路径规划问题与递归神经网络(RNN)模型结合，采用基于逻辑方法确定默认路径，然后应用历史最短路径数据训练RNN，最后使用地图更新算法寻找动态最短路径。王润泽等人[14]通过改进的动态蚁群算法来建立动态路径规划模型，该模型能够根据道路拥堵级别和动态路网阻抗的变化动态规划车辆行驶路径。

虽然上述研究成果提供了多种路径的规划方法，但是仍存在一些缺陷：

1)基于路网拓扑结构的路径规划属于静态优化策略，大部分只考虑距离因素，没有考虑城市交通网络的动态性，城市交通网络的交通状态随时间变化，此刻选择的最优路径，在下一时段就可能是最拥堵的路径。

2)基于交通大数据的路径优化研究成果，是结合当前的交通网络的路况信息和路网拓扑结构的路径规划策略，但是，这些策略中仅考虑了1个或2个交通因素。在实际交通网络中，影响行驶路径的因素有很多，如距离、行驶时间、能耗、拥堵程度、个人偏好等。

3)兰州市是甘肃省的省会城市，地处中国西北，是典型的带状组团式结构，城区主要坐落于河谷地狭长的地带内。由于地形先天不足以及道路设施规划不合理，使得其交通时常发生拥堵甚至瘫痪的状况。

基于上述考虑，本文把多因素结合在改进的Viterbi算法中，建立基于实时交通状态的多因素约束的交通路径规划模型。以兰州市出租车GPS轨迹数据为基础，对兰州市城市交通网络的路径规划进行实证研究。

1 构建基于有向多重加权复杂网络的交通网络模型

1.1 构建有向多重加权复杂网络

针对城市路网的拓扑结构，采用主方法[15]构建城市交通复杂网络模型。主方法在建立路网模型时是将实际路网中的交叉路口和路段分别抽象为复杂网络中的节点和连边，保留了路网的空间分布特性。根据路段的交通流方向可将道路分为单向和双向车道，由于各个路段不同方向的交通流特性可用多个参数刻画，比如路段距离、车辆行驶时间等，因此，在考虑各个路段的交通流方向、交通流特性及动态性时，城市交通网络便可抽象为动态有向多重加权复杂网络。

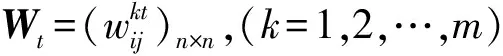
1.2 交通网络模型多重权重属性选择

1)路段长度。

2)车辆行驶时间。

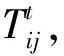
(1)

其中，vsw表示在观测时间段t在路段(vi,vj)上第s辆出租车的第w个瞬时速度，ms表示在该时间段内在该路段上第s辆出租车轨迹点之和，n表示该时间段内在该路段上的出租车总数。

3)交通流密度。

交通流密度[17]指某一时刻同方向单位长度路段上的车辆总数。该指标表示在一条道路上车辆的密集程度，能够反映交通拥堵程度，交通流密度越小，表示道路越畅通，反之则说明道路越拥堵。在观测时间段t内其计算公式为：

(2)

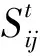
4)车道时间占有率。

车道时间占有率[18]指所有被观测的车辆通过路段(vi,vj)所用时间的总和与观测时间t的比值，其数值越小，说明车辆经过该路段花费时间越少，代表道路越通畅，反之代表越拥堵。其计算公式如式(3)：

(3)

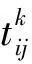
1.3 基于综合赋权法的权重分配

用多重权重属性评价路段的交通状态时，不同属性在评价模型中的重要程度不同，权重值反映了各属性在模型中所起的作用，因此，需要确定各类属性在模型中的权重。其确定方法主要有主、客观赋权法以及两者的结合——综合赋权法[19]。综合赋权法既能借鉴决策者的专家经验，又能客观反映属性值的变化分布规律。比如，司机和交通管理者对城市路网的交通状态随时间的演化特点比较了解，这属于专家经验。通过城市交通大数据分析交通状态变化趋势，以样本数据的分布特征为依据，确定多权重属性的权重分配，这属于客观赋权法。本文采用综合赋权法对交通网络模型的多权重属性进行权重分配。

1.3.1 基于层次分析法的主观赋权法

层次分析法[20](Analytic Hierarchy Process，AHP)是主观赋权法中使用频率最高的一种确定多因素权重的方法。在交通领域，它是根据交通管理者与有经验的司机的主观经验判断，通过比较因素之间的重要程度，构造判断矩阵，再利用特征根法求解各因素的权重占比。AHP确定因素的权重具体步骤为：

Step1构造判断矩阵：已知影响因素为路段长度、车辆行驶时间、交通流密度、车道占有率，根据Saaty等提出的1～9级标度法构造判断矩阵B：

Step2计算权重：采用特征根法计算权重。计算判断矩阵B的最大特征值λmax及其对应的特征向量α，将α进行归一化处理，归一化后的结果即为对应因素的权重。

Step3一致性检验：对判断矩阵B进行一致性检验。首先，计算一致性指标CI(n)=(λmax-n)/(n-1)，其中n表示因素个数。然后，RI(n)的值在《平均随机一致性指标》表中可以得到。最后，计算一致性比例CR=CI/RI，如果CR<0.1,则可认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正。

CR(n)=CI(n)/RI(n)

(4)

其中，CI(n)=(λmax-n)/(n-1)，n=4，RI(4)=0.89。由于CR(4)=0.0503<0.1，故满足一致性要求。

1.3.2 基于信息熵的客观赋权法

属性的无序度可以用信息熵[21]来刻画，它的计算是基于实际的交通数据，因此该方法计算得到的各属性的权重不受人的主观喜好控制，可以客观反映属性值的变化分布规律。基于信息熵的权重计算步骤为：

Step1权重属性标准化：

Step2计算各属性的信息熵：

(5)

Step3计算各属性的客观权重：

(6)

1.3.3 确定综合权重分配

综合赋权法既能借鉴决策者的专家经验，又能客观地反映属性值的变化分布规律。其计算公式如式(7)：

kj=ανj+βμj

(7)

其中，α与β分别为主、客观权重的占比系数，且α+β=1。

1.4 确定路阻函数

由于本文选择路段长度、车辆行驶时间、交通流密度、车道占有率这4个指标作为交通网络模型的多重权重属性,故有向加权复杂网络模型的路阻函数[22]定义时要考虑这4个属性特征。另外，交通网络是动态网络，在不同时段，每个路段的交通状态动态地变化，最优路径的规划时要以实时路况信息为依据，因此，每个路段在某时间段的路阻函数定义如下：

(8)

2 基于改进Viterbi算法的最优路径规划

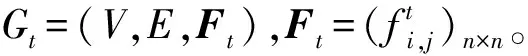
图1给出了将有向加权复杂网络转换为篱笆有向网络的示例，其中图1(a)是一个有向加权复杂网络，图1(b)为其转化后以1号节点为起点的篱笆有向网络，即Viterbi图。在Viterbi图中，圆圈内的数字代表节点编号，每条边上的数字大小刻画了不同的权重大小。将有向加权复杂网络转换为篱笆有向网络的方法步骤：1)从源节点开始，保留源节点与其相邻节点的图结构，并将这些邻居节点放入第1状态节点集合X1={x1i,i=1,2,…n1}中；2)将X1中的每个节点作为新起点进行遍历，保留与其相邻节点的图结构，将集合X1中节点的所有邻居节点放入第2状态节点集合X2={x2j,j=1,2,…n2}中；3)再对集合X2进行步骤2的操作，一直进行下去，直到遍历完所有节点，最终形成的图结构，即为篱笆有向加权网络。

(a)有向加权复杂网络

基于改进的Viterbi算法的最优路径规划算法如算法1所示。使用该算法对图1中从源节点1到其他节点的最优路径进行求解的过程如图2所示。这里，最优路径的定义是为了与传统最短路径进行区分，最短路径是指起、终点间行驶距离最短的路径，而最优路径是指起、终点间道路阻抗值总和最小的路径。

由图2(b.1)可知，在第2状态的计算中从节点1到节点1、2、5均存在多条路径，在到达同一节点(例如5号节点)的多条路径(1→5、1→2→5)中选择保留最短路径(1→5)，删除其余路径(1→2→5)，进而得到图2(b.2)。后续状态的计算方法同上。整个计算中每一步都保留局部最优解，因此大大减少了计算复杂度。最终在图2(d.2)中得到最优路径结果如表1所示。

(a)第1状态的计算

表1 1号节点到其他各节点的最优路径及路径长度

算法1 基于改进Viterbi算法的最优路径规划算法

输入：Gt=(V,E,Ft),源节点vs

输出：在t时刻，vs到其他节点的最优路径

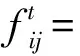
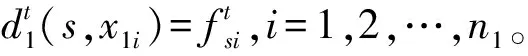
步骤3 计算源节点vs到第2个状态X2的所有节点的最短路径长度。对于集合X2中的第j个节点x2j，从源节点vs到x2j的最短路径为经过第一状态节点集合任何一个节点x1i的路径与直接到达的路径中的较短路径，即最短路径长度为：

步骤4 类似步骤3，计算出从vs到第3,第4，…直到最后一个状态的所有节点的最短路径长度，经过最短路径长度的节点构成了源节点vs到其他所有节点的最优路径。

3 研究区域及数据集

兰州市是甘肃省的省会城市，地处中国西北，是典型的带状组团式结构，城区主要坐落于河谷地狭长的地带内。兰州市5个城区中城关区由于行政单位较多、中小学幼儿园聚集使得上下班高峰期车流量过大，极易发生拥堵。

本文进行最优路径规划的实验路网选取的是城关区从南关十字到汽车东站的一片区域，如图3所示。该区域西起南关十字，东至汽车东站，路网包括庆阳路、甘南路、平凉路等在内的35个路段。其中甘南路部分路段(西起金昌南路，东至平凉路)、畅家巷的部分路段(东起金昌南路，西至静宁南路)为单向车道，其他路段均为双向车道。

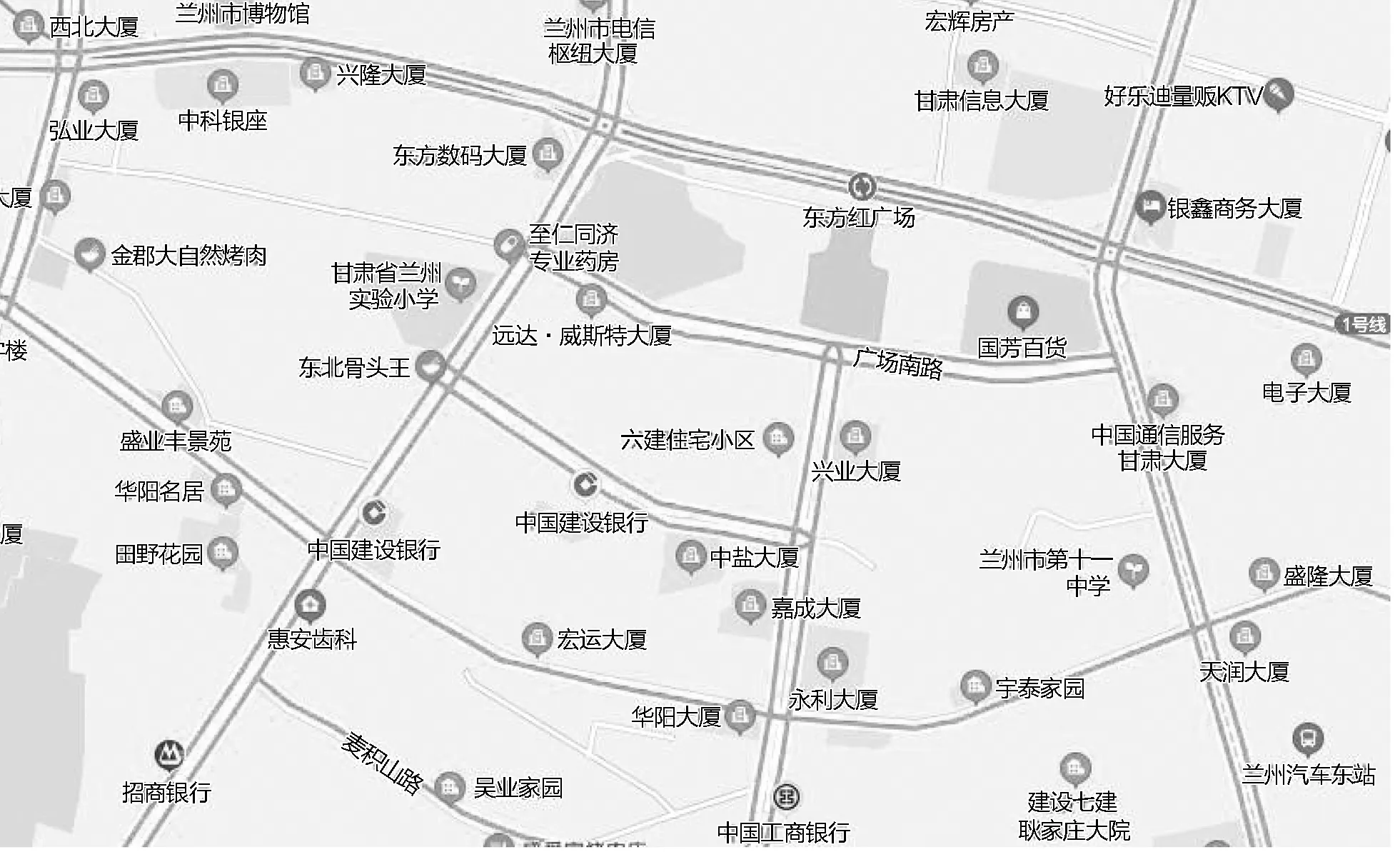
图3 研究区域

实验使用的是兰州市3000辆出租车的GPS轨迹数据，数据采集时间为2017年3月6日—2017年3月12日。该数据集是连续7天的数据，具有一定的代表性，恰好体现了工作日和休息日的城市交通状态和居民出行规律。在使用前需对原始GPS数据预处理，首先，清理原始GPS数据中的离群点、缺失值、冗余值等；然后，通过MNTG(Minnesota Traffic Generator)获得兰州市主城区路网拓扑信息；最后，将轨迹数据匹配到路网信息上。

4 实验及结果分析

首先，以30 min为观测时间长度，对每天24 h的交通基础数据进行统计，计算城市路网每个路段的路段长度、车辆行驶时间、交通流密度、车道占有率的值；然后，计算1.3节中3种方法下的权重系数，进而得到实验路段的阻抗值；最后，对优化构建的有向多重加权复杂网络模型采用改进Viterbi算法求解最优路径。由于城市交通网络状态随时间变化，故构建的复杂网络随时间动态变化。计算不同因素的权重时，在AHP中，本文借助MATLAB里的eig函数来求解判断矩阵的最大特征值及对应的特征向量，进而得到不同因素的权重；在熵权法中，本文以轨迹大数据为基础，通过MATLAB语言编程，得到该方法下的不同因素的权重；在综合赋权法中，以主、客观赋权占比为6∶4来计算得到不同因素的权重。表2给出了不同方法在不同时间段下各属性的权重系数。

表2 不同方法所得高峰期和非高峰期权重系数

由于篇幅所限，仅对2个具有代表性的时段(早高峰、非高峰期)进行分析。图4(a)和图4(b)为相同起终点(起点南关十字，终点汽车东站)时，早高峰时段7:30—8:00和非高峰时段5:30—6:00在不同方法下得到的最优路径规划结果。

由图4(b)可知，在非高峰时段基于主观赋权和综合赋权的最优路径一致，且最优路径大部分和最短距离路径重合。由此可见，主观赋权体现了用户的个人偏好和经验，在非高峰期是较好的路径选择方法。但是该方法并不适合在交通高峰期使用，由图4(a)可知，基于主观赋权最优路径和综合赋权的最优路径有部分路段并不重合，这是由于在高峰期，路径选择受交通状态的影响比较大，使用考虑了主观和客观因素的综合赋权法得到的路径才是最优路径。另外，高峰期最优路径和最短路径没有重合部分，因为距离最短路径上的甘南路是高峰期拥堵比较严重的路段，所以该路段不会出现在由主观赋权和综合赋权得到的最优路径上。

(a)7:30—8:00

本文用定性指标(影响因素个数)与定量指标(路径阻抗值的大小)来对不同算法的好坏进行评价。传统的最短路径算法仅考虑距离这个单一的因素来进行路径规划，而本文提出的最优路径规划算法通过充分考虑多种交通流因素及用户的偏好与经验，使得推荐的最优路径既满足用户的个性化需求，又符合城市路网的交通状态，为用户提供的出行路径更加合理。此外，综合赋权法在早高峰和非高峰期得到的最优路径的阻抗值分别为2.6287、4.1057，均低于由主观赋权法得到的阻抗值2.6361、4.1768。这说明本文提出的综合赋权最优路径规划算法更加科学合理。

5 结束语

合理的路径规划方案不仅能使人们的出行更高效、快捷，同时也能缓解交通压力，有助于交通管理和控制。本文提出的动态最优路径规划算法以轨迹大数据和城市路网拓扑结构为基础，既考虑了城市动态变化的交通状态，又考虑了出行用户的个性化需求与偏好。采用基于层次分析法和熵权法相结合的综合赋权法，对优化构建的有向多重加权复杂网络模型采用改进的Viterbi算法求解最优路径，提高了算法效率。利用兰州市真实的出租车GPS数据，验证了该算法的实效性。该算法构建的有向多重加权复杂网络模型具有很好的推广性，可以考虑更多交通影响因素推荐最优出行路径，同时也适合大规模城市交通网络的路径规划。今后笔者将研究如何提高城市交通状态的精确判断，解决不同约束下的路线规划问题，为城市居民出行提供参考。