基于聚类欠采样的集成分类算法

周传华，朱俊杰，徐文倩，邓佳佳

(1.安徽工业大学管理科学与工程学院,安徽 马鞍山 243000;2.中国科学技术大学计算机科学与技术学院,安徽 合肥 230000)

0 引 言

数据的不平衡现象一直存在并已引起了广泛关注[1]。例如软件缺陷预测[2]、入侵检测[3-4]、信用卡欺诈[5]等应用领域中的数据倾斜。研究表明，当某个类别的数量远大于其他类别的数量时，传统的分类算法更加关注多数类样本。如何提高模型对少数类样本的分类性能，是目前亟待解决的重要问题。

不平衡数据不同于噪声和离群值，它不是由数据生成过程中的错误引起的问题，而是由于大多数应用领域的本身性质而导致的，因此无法避免。目前对不平衡数据的处理方法主要分为2类[6]。第1类是数据层面，首先进行数据预处理，使用重采样方法平衡具有倾斜度的类分布，这类方法主要包括对少数类的过采样，以及对多数类的欠采样；第2类是算法层面，通过修改算法对数据集的偏差，主要有代价敏感学习[7-8]和集成学习[9-10]。代价敏感学习是通过为少数类样本分配更高的成本值并优化其成本错误目标函数。集成学习是通过前面的分类器增加错误分类的样本权重来解决不平衡问题。本文将数据层面的欠采样方法与算法层面的集成学习相结合，并将其应用于不平衡分类问题中。

欠采样是通过删除大多数样本来保持数据平衡[11]。Kubat等[12]提出，欠采样算法的效果优于过采样。文献[13]提出了随机欠采样(RUS)能够快速从多数样本中随机选取并删除一些样本达到样本分布平衡。文献[14]提出了基于聚类的欠采样(CBU)，使多数类聚类簇数与少数类中数据点数相同，能够有效排除掉噪声点。文献[15]提出了一种改进的K-means欠采样，能够根据聚类分布以及从多数类到少数类聚类中心的距离来选择样本，提高边界样本的采样率。但是在数据处理中仍然存在着分类效果不理想的问题。与上述方法相比，数据处理与集成学习相结合的方法已被证明对处理复杂的类分布问题更有效。文献[16]提出了将RUS与AdaBoost相结合，在训练弱分类器之前，使用RUS方法得到训练数据集，用于弱分类器训练，每一次迭代利用RUS更新训练样本，提高模型的分类性能。文献[17]提出了KacBag算法将聚类欠采样与代价敏感相结合，根据权重的大小进行欠采样，选取权重较大的多数类样本，将其与少数类样本结合，提高对少数类的分类性能。

为了解决上述问题，本文提出聚类欠采样的集成算法(CU-AdaCost)，通过实验表明，该算法在数据处理层面能够有效保留信息特征较强的样本，并通过集成算法提高对少数类样本的分类性能。

1 相关工作

1.1 K-means算法

K-means算法是经典的基于划分的聚类方法，对于给定的样本集，按照样本之间的距离大小，将样本集划分为k个簇[18]。K-means算法步骤如下：

输入：数据集X={x1,x2,…,xn}，生成簇个数k

输出：k个簇集{c1,c2,…,ck}

Step1在样本数据集中随机选取k个样本点作为k个数据簇的初始聚类中心。

Step2利用欧氏距离计算出数据集中每个样本点与k个初始簇中心的距离，将数据集中每个样本划分到与其距离最短的中心所在簇内。

Step3重新计算每个簇内的样本均值作为新的簇中心。

Step4为了达到最小化误差平方和准则函数，重复运行Step2和Step3的迭代步骤，直至达到算法最大迭代次数或簇类中心不再变化，否则继续。

其中，E是数据集中所有样本的平方误差和，k为聚类簇的个数，p是空间中的点，表示给定对象，mi是簇ci的均值。

1.2 AdaBoost算法

AdaBoost算法是Boosting算法的具体实现，近年来一直倍受关注[19]。该算法步骤如下：

1)初始化训练数据的权值分布Di，最初每个样本都被赋予相同的权值wi=1/N，N为训练样本个数。

2)训练弱分类器Ht。为了生成T个基分类器，需进行T次迭代。在第t次迭代中，根据训练数据的权值分布生成基分类器Ht，并计算该基分类器在训练集上的分类误差et，再计算弱分类器在最终分类器中所占的权重。在此过程中，如果某个训练样本点被Ht正确分类，则在构造下一个训练集中，它对应的权重要减小，若样本被错误分类，权重要增大。

3)加大分类误差率et小的弱分类器的权重，使得这些弱分类器在迭代中起决定性作用。降低误差率et大的弱分类器的权重，将各个训练得到的弱分类器组合成强分类器。

2 改进的聚类欠采样算法

对于数据层面的思想，主要是利用K-means算法对多数类别做样本聚类，找出各簇区域中所需的多数类样本后，剔除其余样本，重新与少数类别形成均衡训练集。然而K-means算法在选取初始聚类中心时，随机性强，易选择边缘点和噪声点，面临局部最优化，无法得到全局最优解，最终导致模型极不稳定。针对此问题，本文提出改进的K-means算法，计算每2个样本之间的维度加权后的欧氏距离之和[20]，并选取最小距离之和的样本点作为第一个簇心。引入属性权值可以加大数据属性的区分程度，使得边界点、噪声点与聚类中心的距离变大而不会被选中，则第一个簇心点易落入密集区域，视为安全样本。然后选取离前n个簇心最大距离之和的样本点做下一个簇心[21]。通过计算各簇心与附近样本点之间的距离，有效地删减距离簇心较远的样本，在遵循多数类样本数量减少的前提下，最大限度地保证多数类样本的信息含量，最终得到新的多数类样本集。

改进的聚类欠采样算法步骤如下：

输入：数据集D={x1,x2,…,xn}，样本点xi={xi1,xi2,…,xim},1≤i≤n，m为维度，多数类样本集合为Dmaj，簇的个数为c，欠采样的样本个数为N

输出：新的数据集D*

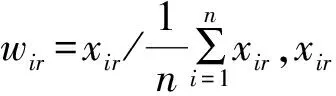
Step2计算出最小距离之和的样本被视为首个样本簇心点，将此样本视为第一个簇心。计算任意样本与第1个簇心之间的距离，取最大距离的样本为第2个簇心，以此类推，离前2个簇心最大距离和的样本为第3个簇心,一直取到第c个簇心。

Step3选取与簇心距离最小的N-c个样本，每个簇选取(N-c)/c个样本，最终得到含有N个样本的样本集[22]。

Step4将得到的欠采样多数类样本与原来的少数类样本结合成新数据集D*。

3 融合聚类欠采样的集成算法

为了提高基分类器对不平衡数据的分类，利用算法的融合，首先对训练数据集中多数类样本采用聚类欠采样算法保留下包含较多特征信息的样本，使得多数类样本和少数类样本的数量大致相等，重构新的均衡数据集；然后选择CART树作为集成算法的基分类器，同时在集成算法的每次迭代中，被分类正确的多数类样本的权值会降低，对于弱分类器的影响将变小。于是在样本权重更新的过程中引入代价敏感函数β，本文将采取AdaC2算法中样本的更新策略[23]，正确分类时β+(c)=-0.5Ci+0.5，错误分类时β-(c)=0.5Ci+0.5。其中Ci为第i个被错分类实例的代价。

CU-AdaCost算法中算法层面的具体步骤如下：

Step1得到新的均衡训练集S={(x1,y1),(x2,y2),…,(xi,yi)|i=1,2,…，N,yi∈{-1,1}}，初始化样本分布权值，每个样本赋予相同的权重。

Step2在T次迭代中，根据训练样本的权值分布进行训练得到基分类器gT，并计算分类误差err(gT)。

Step5返回一个强分类器。

4 实 验

4.1 实验数据集

为了验证CU-AdaCost算法的分类性能，本文采用国际机器学习标准库UCI数据集中的6组数据进行对比实验。其中bank、ionosphere是二分类数据集；segment、ecoli、abalone、glass都是多分类数据集。由于本文主要研究二分类的情况，故选择将数据集中多分类数据通过一定的手段转换成二分类数据。将segment数据集中标签为“4”的设为少数类，其余为多数类；将ecoli数据集中标签为“pp”“om”的设为少数类，其余为多数类；将abalone数据集中标签为“F”的设为少数类，其余为多数类；将glass数据集中标签为“7”的设为少数类，其余为多数类。不平衡率为多数类样本与少数类样本数量比值。数据集描述如表1所示。

表1 不平衡数据的基本信息

4.2 评价指标

对于分类问题，一般使用分类精度来评价一个模型的好坏。但在不平衡数据中，传统的分类算法会倾向于多数类样本，这时仅仅靠准确率来判别是不妥当的。因此本文选用分类问题中的其他评价指标对CU-AdaCost算法进行有效性验证，评价指标为F-measure值以及AUC值。为了更直观地给出这些评价指标的计算公式，需要用到混淆矩阵，其真实结果与预测结果划分为4类组合，如表2所示。

表2 混淆矩阵

评估指标定义如下：

1)查准率：分类器能正确分类的正例样本个数在所有分类为正例的样本中所占的比例。

2)召回率：分类器能正确分类的正例样本个数在所有正例样本中所占的比例。

3)F1-measure综合反映了分类器对于不平衡数据分类的性能。

4)AUC(Area Under roc Curve)值指的是ROC曲线下的面积。ROC曲线用来衡量算法分类结果的优劣程度，曲线越靠近左上方，算法的性能越好。当ROC曲线出现交叉时，这时则通过计算横坐标x轴与ROC曲线围成的面积的累加来判断。如果AUC数值越大，则算法的整体的分类性能越好[24]。

4.3 实验结果与分析

为了评价本文算法对不平衡数据的分类结果，使用AdaBoost、AdaCost、RUS-AdaCost、kmeansU-AdaCost算法与CU-AdaCost算法进行实验对比。本文算法中的参数N对应着各数据集中少数类样本的数量，c为聚类的簇数，本文选定的簇数为20。算法均采用CART树作为基分类器。本文实验在Jupyter Notebook中运行，采用的是十折十次交叉验证，每次实验将样本随机划分，80%为训练集，20%为测试集，实验最终结果取其均值。表3、表4为5种算法在不同的数据集中得出的F1-measure值和AUC值。表格中列举了CU-AdaCost算法与其他对比算法在各个数据集下的评价指标值。每列数据的最高评价值用粗体标注。

表3 各算法在不同数据集上的F1-measure值比较

表4 各算法在不同数据集上的AUC值比较

从上述实验对比结果中可以看出，CU-AdaCost算法在各个数据集上的分类性能均高于kmeansU-AdaCost算法，甚至在不平衡率较高的数据集中，F1-measure值、AUC值更是提高至99%、82.99%，对少数类样本的分类精度有着明显提升，表明采用维度加权之后的欧氏距离更能有效地区分出信息特征较强的样本，且有效地规避局部最优化。RUS-AdaCost的算法在abalone数据集上表现不错，这是因为CU-AdaCost在密集区域划分簇时，簇间样本的维度加权后的欧氏距离较小的样本无法精准划分，可能会将此类样本点重复使用，导致学习性能的下降，但CU-AdaCost处理其他数据集的分类效果仍要高于RUS-AdaCost算法。

为了更直观地观察到各算法的分类性能，图1和图2分别绘制了各算法在数据集上的F1-measure值和AUC值折线图。由图可知，CU-AdaCost算法在不平衡数据集上的分类性能均强于AdaBoost和AdaCost，说明对数据进行重采样是有明显效果的，改进的聚类欠采样也能够选出具有代表性的样本，再与集成算法相结合，更能提高整体模型对少数类样本的识别精确度。综上分析，相比其他算法，本文提出的CU-AdaCost算法处理不平衡数据的能力更强，具有一定的鲁棒性。

图1 F1-meansure值变化曲线

图2 AUC值变化曲线

5 结束语

针对现有的算法分类效果不理想的问题，本文提出了一种基于聚类欠采样的集成算法，结合了聚类、欠采样与集成的思想，有效规避了噪声点对分类器的影响，并提高对少数类的分类性能。实验结果表明，CU-AdaCost算法相较于传统算法的分类性能有显著提升。但对于簇间样本的维度加权后的欧氏距离较小的样本无法精准划分，尚有改进的空间。