高速列车风与自然风耦合致输电线路跨越封网风偏的控制
谢洪平,江力强,刘亮,刘寅莹,何畅,曹枚根
(1.江苏省电力有限公司建设分公司,江苏 南京 210000;2.中南大学 土木工程学院,湖南 长沙 410075;3.北方工业大学 土木工程学院,北京 100144)
我国计划于2035年建成高速铁路7×104km,从而形成6条主轴、7条走廊和8条通道的国家未来综合立体交通网络[1]。国家电网有限公司着眼于以“特高压”为代表之一的“新基建”的建设,逐渐建成各大区域电网。同为线路工程,输电线路与高速铁路在空间中的交叉跨越日益频繁。在输电线路交叉区域的施工过程中,为确保高速列车运营安全,需要在输电线路与高速铁路之间设置封网结构[2]。封网结构的受力面积大,刚度较小,在列车风和自然风的耦合作用下容易产生较大变形。封网风偏后很容易侵入高铁线路界限,造成其上部施工安全事故。然而,目前针对封网结构风致振动控制的研究还不足,开展高速列车耦合风作用下输电线路跨越封网风偏控制的研究具有重要意义。
封网结构已广泛应用到工程实际中。孙伟军等人将全封闭绝缘封网应用于浙江省首例500 kV输电线路跨越高铁施工中[3];而防护横梁架设封网的方法也逐渐体现在跨越工程中[4];张马林等[5]提出利用本塔辅助横担封网跨越高速铁路的施工方法;南方电网的滇西北工程采用了悬索斜封网跨越高速铁路的施工方案[6]。
国内外学者对列车风开展了十分广泛的研究。Gallagher[7]和Bell等[8]分别采用眼镜蛇探针测试了移动列车和静止列车模型周围的列车风,测试结果取得了较好的一致性;牛纪强等[9]、田红旗[10]和柳润东等[11]研究了高速列车会车过程中产生的压力波对列车和周围防风措施带来的影响;周小刚等[12]研究了钢箱梁斜拉桥上列车风及其风致振动响应;高峰等[13]提出列车风引起的输电线路振动频率与输电线路自振频率接近,易引发共振。
封网结构是典型的悬索结构。由于悬索结构的刚度较小,易在外力作用下产生较大变形,控制其风偏尤为重要[14-16]。董新胜等[17]研究了绝缘护套对输电线路导线风偏的影响。
综上所述,以往研究中多为高速列车风及其引起的结构响应,目前缺乏针对封网结构风致振动控制的规范和指南。而在实际工程中,列车风通常与自然风相耦合出现,在输电线路与高速铁路的交叉区域,自然风风速一般大于高铁风风速,因此自然风也应为重点研究对象。另外,列车风与自然风相耦合后会产生紊流,这可能放大封网结构的风偏响应。为研究列车风与自然风耦合作用下输电线路跨越封网的风偏控制,本文以CRH380A型列车为研究对象,计算列车运行时列车风与自然风耦合风速剖面,建立常见施工封网的数值模型,研究其在耦合风荷载作用下的动力响应,提出封网风偏控制解决方案。
1 高速列车风耦合作用
1.1 耦合高速列车风计算模型
1)高速列车在大于风速为25 m/s的自然风作用下会停止运行,考虑到高速列车风与自然风的最不利耦合作用,本文采用25 m/s风速的自然风与行驶速度为350 km/h的高速列车耦合,分析耦合风对封网结构的影响。
以现役CRH380A动车组作为研究对象,建立列车分析模型,由“头车+中车+尾车”3列编组形式组成[8-9],列车总长L=78 m、高H=3.7 m、宽B=3.38 m。计算模型暂未考虑电弓、车轮、门窗和转向架等部件,并在车厢连接处进行简化处理,如图1所示。
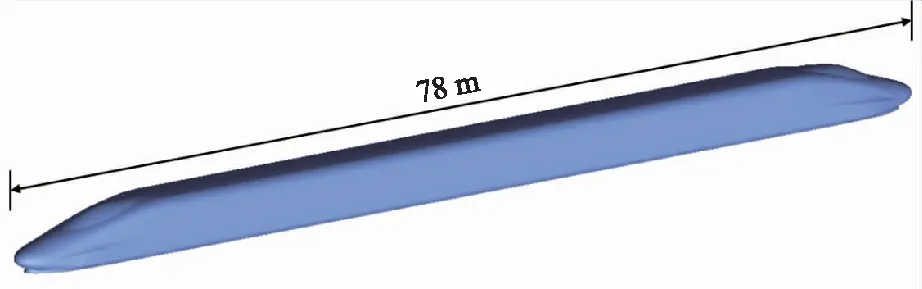
图1 高速列车简化模型Fig.1 Simplified model of high-speed train
基于已有研究结果[10],数值模型采用长600 m、宽150 m和高100 m的计算域,如图2所示。计算域共包括6个面,分别对每个面进行边界定义:计算域的前、后、顶面被定义为对称边界,左侧面被定义为速度入口边界,右侧面被定义为压力出口边界,底面和列车被定义为无滑移壁面边界。为避免计算域边界对列车流场的干扰,列车位于初始位置时,车尾距离计算域入口100 m,车头距计算域中心122 m。采用铺层法[11]考虑列车的移动过程,通过在静止区域和列车移动区域建立1层Interface界面,实现列车移动中的流场信息交换。沿列车车顶正上方布置34个测点,监测距离车顶不同高度处的风速,如图3所示。
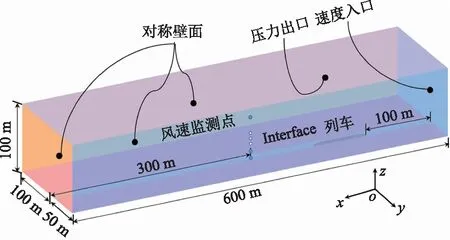
图2 耦合风作用计算域Fig.2 Computational domain of coupled wind load
时速为350 km/h的高速列车风与风速为25 m/s的自然横风耦合后的速度为100.39 m/s,马赫数小于0.3,视为不可压缩流体。采用非定常、黏性、
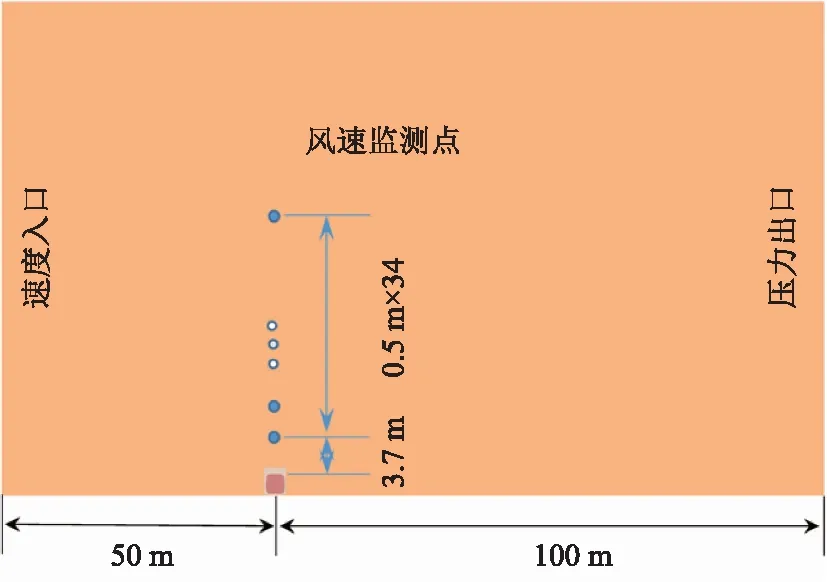
图3 耦合风高度方向测点布置Fig.3 Measuring point layout of coupled wind in height
不可压缩N-S方程和RNGk-ε湍流模型来模拟高速列车的运行过程[18-19]。湍流动能k和耗散率ε方程分别如下:
(1)
(2)
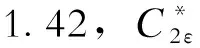
(3)
式中:模型常数C2ε=1.68;模型常数Cμ=0.084 5;应变系数η0=4.38;热膨胀系数β=0.012;时均应变率η=Sk/ε;S为应变率张量的范数。利用Fluent的SIMPLEC方法计算,时间步长取0.008 57 s。
1.2 模型网格划分及验证
本模型采用结构网格与非结构网格相结合的混合网格划分方法。由于静止区域几何构造相对简单,采用结构网格划分,最大尺寸为1.5 m,最小尺寸为0.2 m;移动区域列车结构相对复杂,采用非结构网格,最大尺寸为0.1 m,具体如图4所示。考虑网格精度对模拟结果的敏感性,分别对3种网格(2.10×107稀疏网格、3.18×107中等网格和4.30×107精细网格)下的计算结果与302 km/h时速运行的CRH3动车模型试验结果[12]进行对比(如图5所示),发现采用4.30×107网格的计算结果与动模型试验结果保持更好的计算精度,因此本文采用该类网格划分方式。

图4 高速列车单元划分Fig.4 Element mesh of high-speed train

图5 高速列车风计算结果验证Fig.5 Validation of high-speed train slipstream analyzing results
1.3 耦合高速列车风
列车在垂直于行车方向的25 m/s横风作用下以350 km/h时速穿过时,计算域不同位置处的各向风速有显著差别。列车行进方向出现明显的“头波”和“尾波”,其波峰值和波谷值随高度呈现先增大后快速减小的变化,如图6(a)所示。对于图6(b)所示的横风向,列车明显放大了横风风速作用,2倍高度处的放大因子达到23%,这与我国建筑结构荷载规范[20]中风吹过小山在山顶形成的风速放大效应基本一致,Li等[21]在列车-扁平箱梁系统中观察到列车车肩处的风速加速效应也有相似发现。对于图6(c)中的竖风向,耦合风风速略大于前进方向的结果,这是横风流过列车后在竖直方向形成的1个风速分量造成的。
当跨输电线路跨越高铁时,在其架设高度可能受到列车风和自然横向风的耦合作用,从而产生不利的风偏和风振效应,特别是横风放大效应和“头波+尾波”的冲击效应。通过对高速列车与自然横向风耦合作用下的输电线路跨越封网结构开展数值模拟研究,发现封网结构竖向振动幅度较大,可能侵入高速铁路界限和影响上部输电线路的施工安全,需要增大封网承力索的预张力减小风偏响应。

图6 耦合风作用下的风速曲线Fig.6 Wind speed time curves under coupled wind load
2 输电线路跨越封网耦合风偏响应控制
2.1 输电线路跨越封网结构数值分析模型
针对研究发现的耦合风作用下封网结构竖向风偏过大的问题,本文提出采用风偏控制拉索的方式控制封网结构的竖向风偏作用。采用风偏控制拉索的输电线路跨越高铁施工封网结构如图7所示。
封网结构包括承力索、风偏控制拉索、撑杆等[3]。为探究风偏控制拉索对输电线跨越封网风偏响应的影响,本文设计了2种风偏控制方案,平面布置如图8所示。方案A包含4根风偏控制索,方案B包含8根风偏控制索。封网结构有4根承力索,索间距为8 m。承力索由直径为16 mm的迪尼玛绳组成。封网沿水平方向跨度为300 m,两端均安装在跨越塔架上。封网承力索的初始预张力设为80 kN,封网底部距离列车车顶高度为8 m。为保障各承力索的稳定性和协同工作,封网中部高铁线路正上方共设置9根玻璃钢复合材料撑杆,以维持封网承力索间的距离,并能缓冲输电线路断线等偶然事件。
由于封网结构主要由其承力索、撑杆和风偏控制拉索组成,在数值模型中忽略了其他附属部件,仅考虑承力索、撑杆、风偏控制拉索三者之间的作用。本文基于Abaqus软件建立封网结构及风偏控制拉索的有限元模型,为较好地模拟拉索非线性变形及受力变化,采用B31非线性梁单元模拟封网承力索、风偏控制拉索及撑杆,有限元模型如图8所示,图中①、②、③、④分别表示封网结构的1、2、3、4号索。有限元模型通过施加初始预应力的方式,模拟封网承力索所施加的80 kN预张力。由于跨越塔架与高速铁路的距离较远,在列车风影响范围外,在数值模型中未考虑跨越塔架,而将封网承力索直接固定在支座上。该算例的列车前行方向与封网方向成90°垂直,有限元模型通过施加重力场的方式进行封网承力索找形。高速列车风速及风压简化为集中荷载,施加在承力索的节点上。

图7 采用风偏控制方案的封网结构Fig.7 Sealing net structure adopting wind yaw control scheme
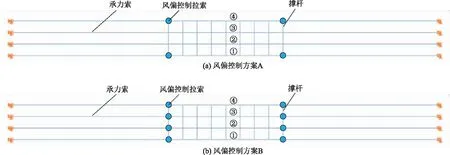
图8 采用风偏控制方案的封网结构数值模型Fig.8 Numerical model of sealing net structure adopting wind yaw control scheme
2.2 封网结构数值模型验证
封网结构的承力索可简化为悬索,其弧垂fa可按下式计算[22]:
(4)
式中:ω为迪尼玛绳单位长度的自重荷载,单位为N/m;Fpre为承力索的预张力,单位为N;l为封网结构的跨度,单位为m。
由于目前封网风偏暂无相关试验或现场实测结果,本文利用弧垂理论计算结果验证数值模型的正确性,共计算了无撑杆时封网结构在承力索预张力分别为20 kN、50 kN、80 kN、110 kN和140 kN这5种工况下的弧垂。在不同张力下,由数值分析得到的结果与式(4)计算得承力索弧垂对比如图9所示。本文建立的承力索数值模型计算结果与理论公式计算结果接近,表明本文建模方法具有较好的计算精度,可用于后续封网结构风偏响应控制分析。
2.3 耦合风致封网结构振动响应控制
2.3.1 封网承力索轴力响应控制
基于已有研究可知,在自然风与高速列车风的耦合作用下,封网中同一根承力索的端部与中部内力响应基本一致。校核封网承力索在风振下的强度时,可仅考虑其端部截面的轴力响应。本文分别对
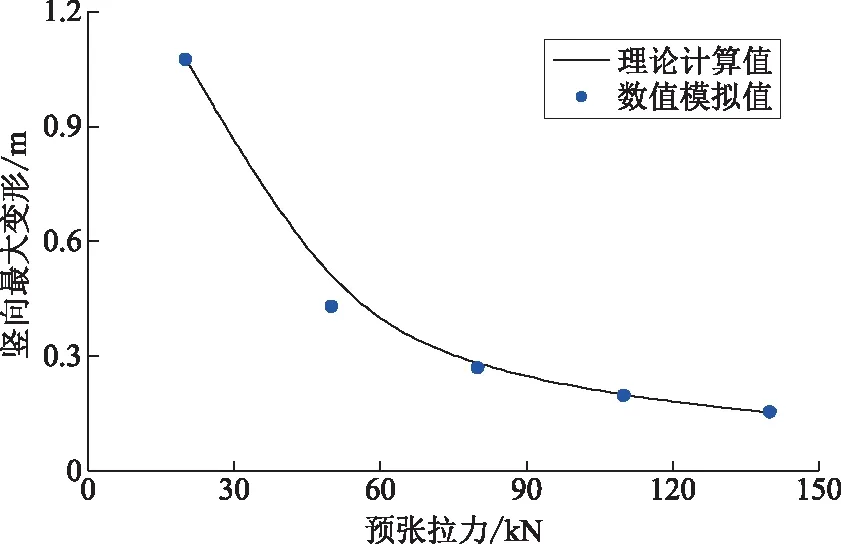
图9 封网结构数值模型验证Fig.9 Numerical model validation of sealing net structure
2种方案1号与3号封网承力索进行内力响应分析,结果如图10所示。
由图10可知,对1号与3号封网承力索采取方案A或未控制时,得到的轴力响应曲线比较光滑,其变化趋势类似于正弦曲线,且二者的曲线几乎重合,与未采取控制时相比,只有峰值发生很小的变化。采取方案B时,轴力变化曲线较为曲折且无规律可言,但轴力值较方案A和未控制时有较大程度的减小。由以上分析可知,方案B对封网的承力索内力响应控制效果更好。预张力为80 kN时,封网承力索最大预张力为81.33 kN,封网承力索最大拉力主要由其预张力决定。对于直径为16 mm的迪尼玛绳,其理论破断拉力为215 kN[22]。在25 m/s自然风与350 km/h时速列车风的耦合作用下,封网承力索强度安全系数为2.6。
2.3.2 封网承力索风偏响应
在耦合高速列车风荷载作用下,封网承力索中部在竖直方向的风致振动位移如图11所示。
在耦合风荷载作用下,封网3号索出现较大幅度的上下振荡,而1号索的变化幅度较小。3号索在采用方案A或未控制时的竖向位移曲线较为接近,其幅值变化为2.42 m和2.55 m。方案B幅值变化为0.94 m,较方案A和未控制时有显著的降低。1号索在采用方案A或方案B时的竖向位移曲线较为接近(方案B值略低于方案A值),在列车通过的过程中其竖向位移曲线接近水平,变化幅度较小且都低于未控制时的竖向位移。由以上分析可知,方案B对封网的竖向位移产生更好的控制效果。在耦合列车风荷载作用下,承力索向下振荡位移小于向上振荡位移。由图11可以看出,封网上下振动幅度较大,在风荷载作用下,封网向下振动可能侵入高速铁路界限。封网向上的位移也可能影响上部施工安全。在进行施工封网的架设时,应考虑此振动距离的影响。

图10 风偏控制方案对承力索轴力的影响Fig.10 Effects on axial force time-history of carrier cables by adopting wind yaw control scheme

图11 风偏控制方案对承力索竖直位移的影响Fig.11 Effects on vertical displacement time-history of carrier cables by adopting wind yaw control scheme
在耦合高速列车风荷载作用下,1号与3号封网承力索横向风偏如图12所示。

图12 风偏控制方案对承力索横向位移的影响Fig.12 Effects on lateral displacement time-history of carrier cables by adopting wind yaw control scheme
方案A与方案B都对1号与3号封网承力索的横向位移控制产生负作用。1号索在采用方案A或方案B时横向位移变化较为接近,只在2.0~2.5 s时程内有较大的差异,其在方案A情况下横向位移峰值达0.42 m,方案B达0.32 m,而未采取控制时为0.32 m。3号索在方案A和方案B时其横向位移同样较为接近,均远大于未控制时的横向位移,方案A时横向位移峰值达0.28 m,方案B时达0.27 m,未控制时仅为0.10 m。基于已有的研究以及上述分析可知,在评估封网承力索结构的横向风偏时,应校核其边承力索的风偏响应。由图12可知,该型封网水平向风偏达0.42 m。在进行施工封网结构设计时,需考虑其水平风偏响应,确保其在风荷载下位置稳定性,保证施工安全。
3 耦合风作用封网风偏控制参数分析
为研究不同风偏控制方案对输电线路跨越施工封网结构在耦合风荷载下的风偏响应控制影响,本节分析不同设计参数的影响,对比2种控制方案与未采取风偏控制方案的内力及风偏响应。研究发现封网安装高度、封网与列车行进方向夹角等参数对封网结构风偏响应影响很小。因此,本文重点考虑封网跨度及封网承力索预张力等参数的影响。
3.1 风偏控制方案对承力索最大轴力的影响
悬索结构在动力作用下的数值模拟具有较强的几何非线性,因此索内张力与动力响应相关,而且受到结构的跨度、弧垂等因素影响。与未采取风偏控制的方案相比,采用风偏控制方案A和方案B的封网结构在不同跨度及预张力下,其封网承力索最大轴力分别见表1、表2和表3。
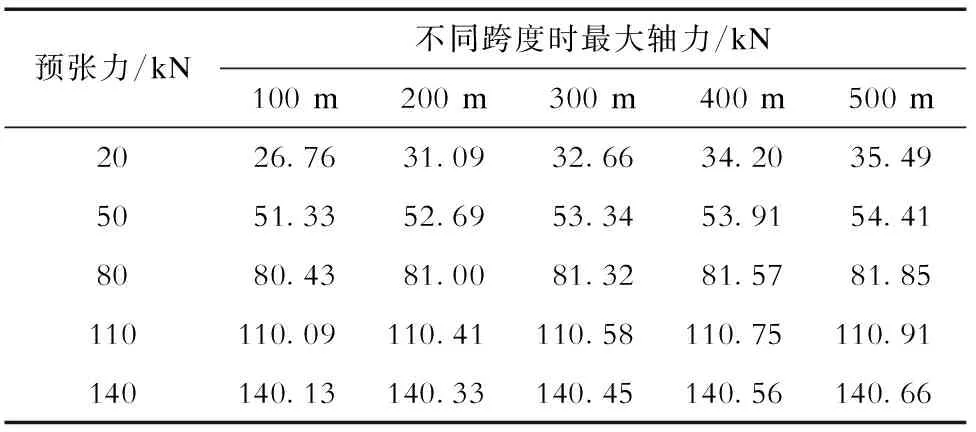
表1 未采用风偏控制时的封网承力索最大轴力Tab.1 Maximum axial forces of sealing net carrier cables without adopting wind yaw control scheme

表2 采用风偏控制方案A时封网承力索最大轴力Tab.2 Maximum axial forces of sealing net carrier cables adopting wind yaw control scheme A
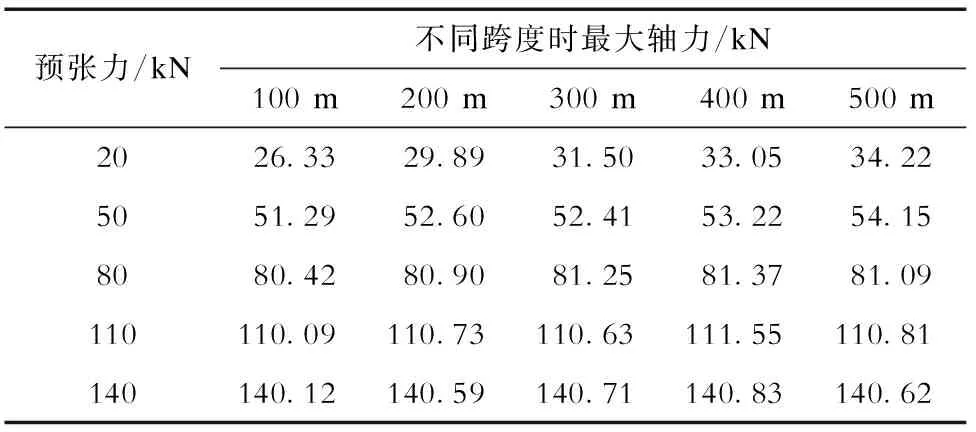
表3 采用风偏控制方案B时封网承力索最大轴力Tab.3 Maximum axial forces of sealing net carrier cables adopting wind yaw control scheme B
定义承力索轴力增量相对值
(5)
式中Fm为承力索所受到的最大轴力。
将风偏控制方案A和方案B情况下的承力索轴力分别与未控制时进行对比,结果如图13所示。
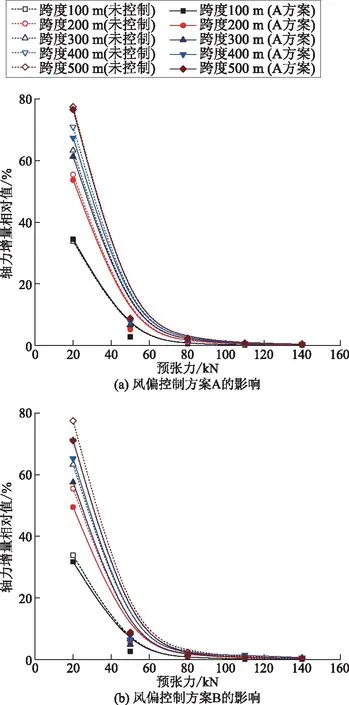
图13 封网承力索轴力增量相对值与预张力关系曲线对比Fig.13 Comparative curves between axial force increment relative values and pre-tension of sealing net load-bearing cable
由图13可知,2种风偏控制方案对承力索轴力的影响并不明显,最大轴力增量相对值与未控制时相比变化不大。整体来说,在不同跨度、不同预张力时,封网承力索的轴力变化较小,其主要由预张力确定。随着预张力增加,承力索最大轴力增量相对值逐渐减小。随着跨度增加,增量相对值逐渐增加。当承力索预张力达80 kN及以上时,采用风偏控制方案和未采用时轴力增量相对值均小于3%,即当封网承力索预张力达80 kN时,可不考虑高速列车及自然风耦合风荷载对承力索轴力的影响。
3.2 风偏控制方案对封网结构水平风偏的影响
不同预张力及跨度下,对风偏控制方案A和方案B情况下的封网水平风偏分别与未控制时进行对比,如图14所示。
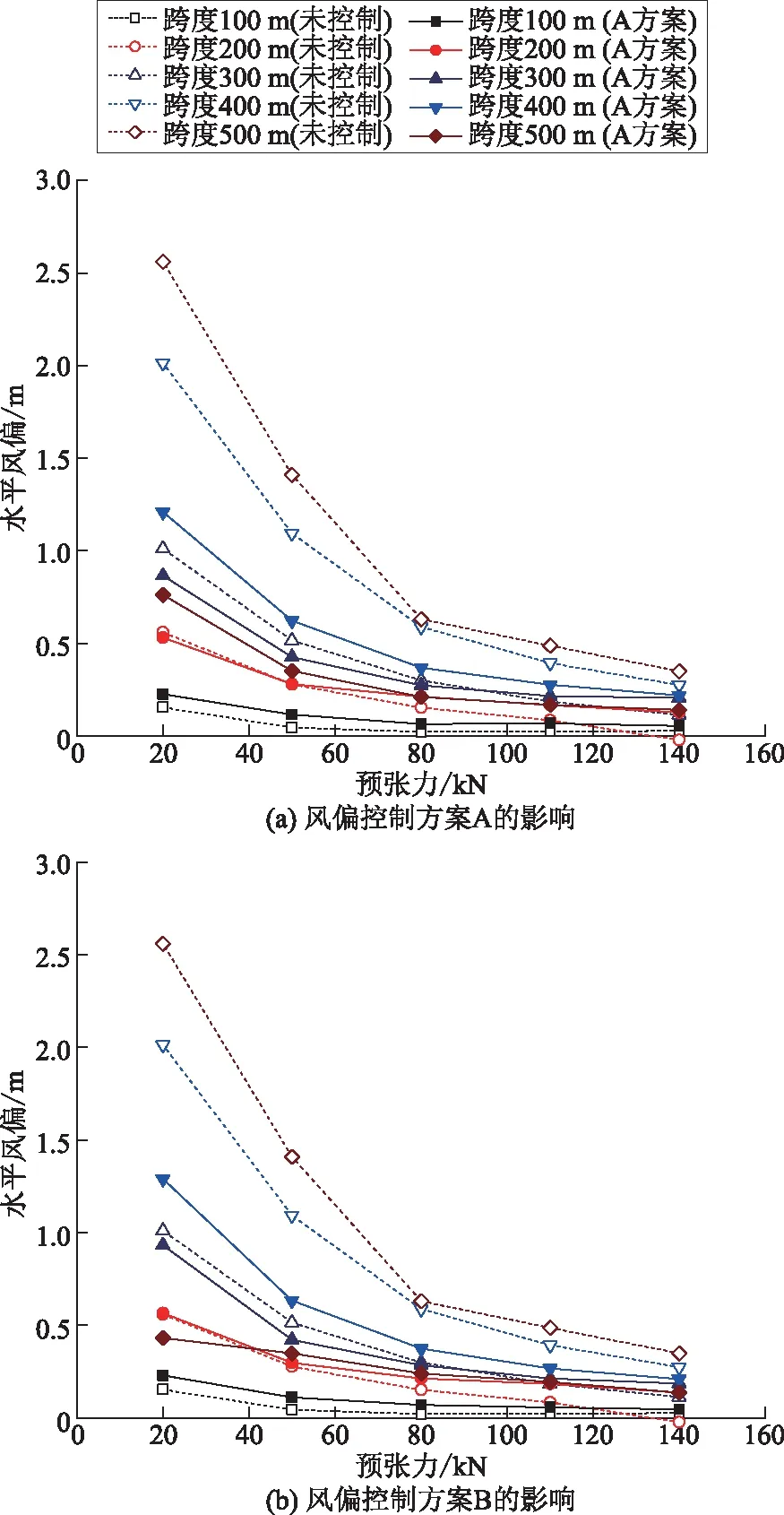
图14 封网结构水平风偏与预张力关系曲线对比Fig.14 Comparative curves between horizontal wind yaw and pre-tension of sealing net
风偏控制方案A、方案B和未控制时这3种情况下,随着承力索预张力的增加,封网水平风偏均呈现减小的趋势。当承力索预张力大于80 kN时,封网水平风偏都趋于稳定。预张力为80 kN时,跨度为500 m的封网未进行风偏控制时水平风偏为0.62 m,采用方案A水平风偏为0.21 m,采用方案B水平风偏为0.24 m。显然,方案A和方案B都对封网水平风偏有较好的控制作用。
3.3 风偏控制方案对封网结构竖向风偏的影响
不同参数下,2种方案封网竖直风偏如图15所示。预张力可有效减小封网的竖向风偏值,此外,在0~400 m的跨度范围内风偏控制拉索可以显著减小封网的风偏值。
对于向上风偏响应,封网发生向上风偏时,其长度缩短,预张力减小,故承力索预张力对封网向上风偏的抑制作用小于向下风偏的抑制作用。随着跨度增加,封网风偏响应逐渐增加。当跨度为500 m的封网预张力为80 kN时,方案A的向上风偏值为0.43 m,方案B的向上风偏值为0.36 m。其他相同参数情况下产生的效果无显著差异。
对于向下风偏响应,大于80 kN的预张力能有效抑制该响应。0~400 m的跨度范围内,在设置有风偏控制拉索的情况下,封网的竖向风偏值均
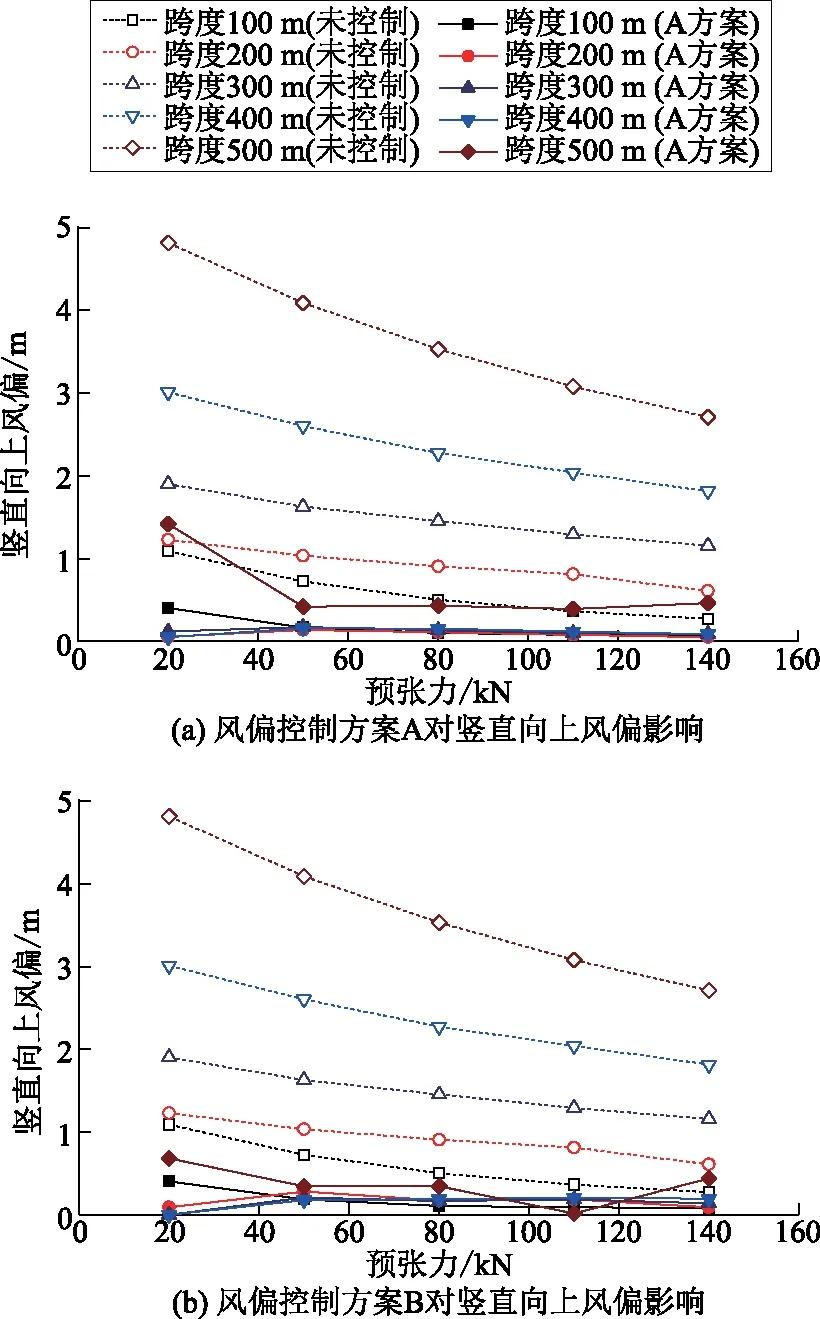
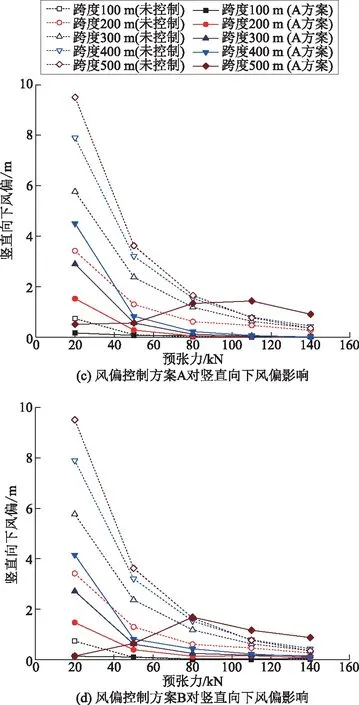
图15 封网结构竖向风偏与预张力关系曲线对比Fig.15 Comparative curves between vertical wind yaw and pre-tension of sealing net
有较大幅度的降低,当跨度为500 m的封网预张力为80 kN时,方案A的向下风偏值为1.34 m,方案B的向下风偏值为1.69 m。其他相同参数情况下产生的效果没有明显的差异。综合来说,方案A优于方案B。
4 结论
本文建立了高速列车与自然风耦合的高速列车风数值计算模型,分析了2种不同方案对封网风偏控制的影响,通过开展不同参数的输电线路跨越封网结构风偏控制动力响应分析,得到如下结论:
a)在封网可能设置的高度范围内,自然风和列车风的耦合作用主要表现为横风放大效应和“头波+尾波”冲击效应,封网承力索轴力主要由其预张力决定。在常见的封网跨度范围内,封网承力索预张力不宜小于80 kN,以减小封网风偏响应,但较大的承力索预应力会导致其安全系数较低,例如直径为16 mm的迪尼玛绳在风速为25 m/s的自然风与时速为350 km/h的列车风耦合作用下,封网承力索强度安全系数为2.6。
b)在高速列车行经封网的过程中,文中所采用的风偏控制方案B对封网承力索轴力响应和竖向的振动位移有显著的控制效果,由于风偏控制拉索的约束控制作用,承力索呈现出高阶振动模式,但振幅明显减小。以300 m跨度、距离高速列车车顶8 m、承力索预张力80 kN的封网结构为例,承力索的竖向位移减少了约66%。但是,方案A和方案B均未对承力索的横向位移起到明显的控制作用。
c)不同预张力及跨度下,2种风偏控制方案对承力索轴力增量的影响不明显,但都对封网水平风偏有较好的控制作用。在预张力为80 kN、跨度为500 m的工况下,方案A承力索水平风偏减小了约67%,向上风偏减小了约75%;方案B水平风偏减小了约62%,向上风偏减小了约85%。因此,2种方案均对风偏响应的控制作用显著,是控制高速列车耦合风作用下封网结构风偏的有效方案,特别是对于大跨度输电线路跨越封网结构。

