基于改进强化学习算法的主动配电网在线等值建模

韦乾龙，唐文虎，江昌旭，钱瞳，李维维，郑杰辉

(1．华南理工大学 电力学院，广东 广州 510641；2．福州大学 电气工程与自动化学院，福建 福州 350116)

随着可再生能源渗透率逐步提高，配电网形态与结构均面临诸多变化[1-3]。主动配电网的源荷形态结构比传统配电网更复杂，管理协调更困难。同时，主动配电网与输电网络进行功率交换时[4-6]，主动配电网中量测装置较少，可观测水平极低，配电网调度员很难获取配电网的详细信息。因此，如何在配电网信息不完全的条件下，建立一个精度较高的配电网等值模型就显得尤为重要。

国内外学者在主动配电网的静态等值模型方面已经做了大量的研究工作。文献[7]不考虑分布式电源的影响，直接使用ZIP负荷模型﹝恒定阻抗模型(Z)、恒定电流模型(I)与恒定功率模型(P)的并联﹞，对配电网进行静态等值。文献[8-9]用等值发电机来表示主动配电网中的分布式发电，并且用PQ节点或PV节点连接在主动配电网中，该模型没有考虑分布式发电的不确定性。文献[10]用一个消耗负功率的负荷来代替分布式风电和光伏发电系统。但是这些模型都不能反映不同分布式发电各自的特征，并且忽略了可再生能源发电的不确定性。因此，许多学者开始考虑不同类型分布式发电的影响以及可再生能源的不确定性。文献[11]利用小波神经网络对不确定性进行预测，文献[12]利用半不变量法对不确定性进行建模，但是无法对此类模型进行在线评估。文献[13]建立了考虑可再生能源空间不确定性的主动配电网模型，并对模型参数进行辨识，解决了分布式电源地理分布不同导致的问题。

主动配电网等值模型的精度不仅取决于模型本身，也取决于参数辨识方法的精度。参数辨识可以看作非线性的最小二乘问题，优化目标是使等值模型输出值与在线监测值的差值最小。该问题存在局部最优，为了解决此类问题，文献[14-16]采用最小二乘(least square，LS)算法建立了单边界节点的等值模型，文献[17]采用遗传算法对参数进行辨识。但是以上算法存在鲁棒性较差、收敛速度慢、对初始值较为敏感等缺点。由于主动配电网的新能源和负荷具有时变特征，导致等值模型的参数也是时变的，因此要求参数辨识方法能够随时更新，进行在线评估。强化学习算法具有较好的在线计算能力，常用于参数在线辨识。文献[18]提出基于时序差分和协方差矩阵的强化学习(function optimization by reinforcement learning，FORL)算法，结果证明该方法较好地解决了维数灾难问题，但是FORL算法在参数时变的条件下求解最优解的能力较弱。

本文考虑不同分布式发电带来的不确定性影响，建立基于改进强化学习(improved function optimization by reinforcement learning，IFORL)算法的主动配电网等值模型。本文的研究工作主要有：

a)建立考虑源荷不确定性的主动配电网等值模型。

b)基于FORL算法，通过引入自适应学习速率，增加路径搜索方向，提出IFORL算法，提高参数辨识精度。

c)提出一种基于权重衰减策略的样本采样方法。

1 主动配电网等值模型

图1为主动配电网的等值模型，包括1个等值风电机组模块、1个等值光伏发电模块和1个等值ZIP负荷模块，其中，(Pin+jQin)为输电网注入配电网的总功率，(Pw+jQw)为配电网中所有风电机组的总功率，(Ppv+jQpv)为配电网中所有光伏发电的总功率，(Pl+Ploss)+j(Ql+Qloss)为配电网中所有负荷的消耗功率以及网络损耗。

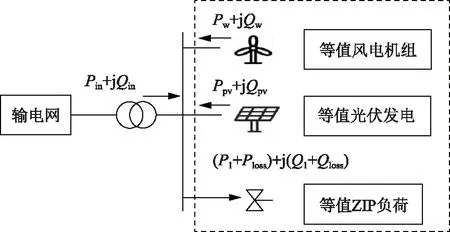
图1 主动配电网的等值模型Fig.1 Equivalent model of active distribution network

根据电路原理，可以得到方程

(Pin+jQin)=-(Pw+jQw)-(Ppv+jQpv)+

(Pl+Ploss)+j(Ql+Qloss).

(1)

1.1 等值风电机组

风电机组的功率输出取决于其功率曲线。风电机组的有功功率

(2)

式中：P(v)为风电机组出力的非线性部分；Pr为风电机组额定功率；v为等值风电机组的风速；vci为切入风速；vr为额定风速；vco为切出风速。

由式(2)可知，风电机组出力曲线分为3段。本文采用式(3)拟合风电机组曲线的非线性部分P(v)[13]：

Pw=w1arcsin(w2v+w3)+w4.

(3)

式中w1、w2、w3、w4为需要辨识的参数。本文假设主动配电网中所有的风电机组都以单位功率因数运行，因此这些风电机组的无功功率均为0。

1.2 等值光伏发电

对于光伏发电系统的建模，本文采取理想光伏发电系统模型，功率输出由以下决定[19]：

Ump(G,T)=Ump,STC+KU(T-TSTC)+

Utln(G/GSTC)+βlg(G/GSTC),

(4)

Imp(G,T)=[Imp,STC+KI(T-TSTC)]G/GSTC,

(5)

Pmp(G,T)=Ump(G,T)Imp(G,T),

(6)

Ppv(G,T)=ηPmp(G,T).

(7)

式(4)—(7)中：Ump(G,T)、Imp(G,T)、Pmp(G,T)分别为光伏发电的电压最大值、电流最大值、有功功率最大值；G为光照强度；T为环境温度；Ump,STC、Imp,STC分别为标准测试条件下光伏发电的电压最大值、电流最大值；GSTC、TSTC分别为标准测试条件下的光照强度和环境温度，GSTC=1 000 W/m2，TSTC=25 ℃；KU、KI分别为电压系数和电流系数；Ut为二极管电压，Ut=kBT/qe，kB为Boltzmann常数，qe为电子电量；β为面板系数；η为逆变器转换效率。KU、KI、Ump,STC、Imp,STC、β、η均为待辨识的参数。

假设光伏发电采取标准的功率因数特性cosφpv实施无功控制，无功功率Qpv由式(8)、(9)得到，待辨识的参数包括阈值有功功率Pth和斜率h：

cosφpv=h(Ppv-Pth)+1，

(8)

(9)

1.3 等值ZIP负荷

本文采用ZIP负荷模型来对配电网的所有负荷进行建模[20]：

(10)

式中：PL(U)、QL(U)分别为节点电压U下，负荷的有功功率和无功功率；ap1、ap2、ap3、aq1、aq2、aq3为待辨识的参数。

2 参数辨识

2.1 IFORL算法基本原理

假设一个最小化的优化问题含有N个控制变量X={x1,x2,…,xN}，IFORL算法采用N个代理，每个代理负责1个维度的搜索。根据马尔科夫性质，将每个代理用1个五元组表示为{Sq,Aq,R,p,π}，其中：Sq={xq}为第q维状态变量xq的状态空间，xq∈[xmin,xmax]；Aq为第q个代理的行为空间；R为从环境中获得的奖励信号；p={p1,p2}分别为搜索路径方向和选择行为的概率；π为代理指导采取行为的策略。

2.2 行为选择

IFORL算法对行为的选择包含3个步骤：首先根据值函数的值对搜索路径进行评估；然后从中选择最佳路径l；最后在路径l上从g个不同的行为中选择最佳的行为。

如果当前单元格状态优于左右2种搜索方向时，原FORL算法在当前状态下只能选择向左或者向右进行搜索，忽略了当前单元格的状态。IFORL算法通过增加第3个搜索方向，即保持在当前单元格方向，对FORL的搜索方向进行改进[21]。

搜索路径更新方程为

(11)

式中：Ll(xq)为状态xq下的路径值；λ1为计算路径值时值函数的权重；将搜索路径l上所有行为的值函数按照降序排列，Al,m为第m个值函数的值；A(xq)为状态xq下值函数的值。

路径方向的搜索概率

(12)

式中：Ll(i,j)为第i个代理的第j个行为的路径值；τ为代理用于在探索和利用之间折衷的参数，其值越大，代表选择所有路径的概率越接近。

确定了搜索方向后，代理在g个行为中选择行为h为最佳行为的概率

(13)

式中A(i,h)为第i个代理选择h行为的值函数的值。

2.3 值函数的更新

为了提高Q-learning算法的收敛速度慢的问题，本文引入通信领域中的资格迹理论来反映过去多步状态与行为对后续策略的影响，进而提升算法的收敛速度和自适应学习能力。

根据FORL算法，第i个代理的第j个行为的值函数Ak+1(i,j)更新公式如下[18]：

Ak+1(i,j)=Ak(i,j)+αδk(i)，

(14)

δk(i)=R+γ(maxAk(i,j)-Ak(i,j)).

(15)

式中：α为学习速率；δk(i)为值函数的增量；γ为折扣因子；k为迭代次数。

FORL算法采取恒定学习速率对值函数进行更新。在k+1次迭代时，如果δk(i)<δk+1(i)<0，说明代理i在行为j下无法得到较大的奖励信号，则说明至少有1个代理采取了不利的行为，并且一定是当前代理导致。如果此时学习效率较大，导致值函数急剧减小，则会降低代理i在下一次选择该行为的概率，导致代理无法寻找最优解，所以此时需要降低学习速率。

IFORL算法通过引入资格迹中的衰减因子λ对恒定的学习速率进行改进，得到自适应的学习速率。假设在第k次迭代中，当值函数增量减小时，学习速率更新公式为：

(16)

式中αk为第k次迭代时的学习速率。因此，IFORL算法中第i个代理的第j个行为的值函数更新公式为

Ak+1(i,j)=Ak(i,j)+αk+1δk(i).

(17)

2.4 等值模型参数辨识

主动配电网中风电、光伏发电和负荷具有随机性，为了追踪其时变特征，本文采用IFORL算法对主动配电网参数进行辨识。在线辨识中，传统的滑动时间窗口认为采样值对模型参数的影响相同，为了使主动配电网等值模型参数能够反映当前时间的参数，本文提出一种随时间按照指数衰减的权重策略[22-23]，该策略可以确保距离当前时刻较近的样本具有较大的权重，从而区分不同时刻采样样本对等值模型参数的影响。

第r个样本的权重

ωr=λn-d.

(18)

式中：n为滑动时间窗口含有的样本数；d为当前采样点在时间窗口中的位置。

为了衡量跨境等值模型的精度，本文采取均方根误差函数来表示目标函数Fy，即

(19)

式中：Xy为需要辨识的参数；yar、yer分别为实际系统和等值系统中第r个结果。

以风电为例，图2为等值风电机组参数在线辨识流程，其中，Xbest为最优参数，kmax为设定的阈值。

图2 等值风电机组参数辨识流程Fig.2 Parameter identification process of equivalent wind turbine

该算法的具体步骤如下：

a)代理根据观测风电机组的风速和所有风电机组的总功率进行采样，然后进行权重更新。

b)计算目标函数，对初始环境状态进行评估。

c)计算奖励信号，判断该选择行为是否有利，更新最优参数Xbest，并将奖励信号发送给等值风电机组模型。

d)在奖励信号的基础上，更新值函数，用于形成指导策略。

e)代理根据策略，选择最佳行为，进而得到最佳辨识参数，每当1个代理完成上述学习过程，令k=k+1，直至k>kmax。

2.5 模型精度验证

等值模型精度验证流程如图3所示。具体步骤如下：

a)更新模型：根据测量装置获得t时刻的气象信息(包括风速、光照强度、环境温度)和电气信息(包括配电网中所有风电机组总有功出力、所有光伏发电总有功出力、边界电压相量、输电网注入配电网的总有功功率和无功功率)，利用IFORL算法分别对不同等值模块进行参数辨识，得到更新的配电网等值模型。

b)抽样：根据气象装置得到t+1时刻预测值，然后输入到t时刻更新后的配电网等值模型，利用拉丁超立方抽样，得到输出功率样本。

c)概率潮流：将上述样本输入到等值模型和实际系统分别进行潮流计算，得到等值模型和实际系统概率潮流解，通过比较等值模型与实际系统的结果，即可得到等值模型的精度。

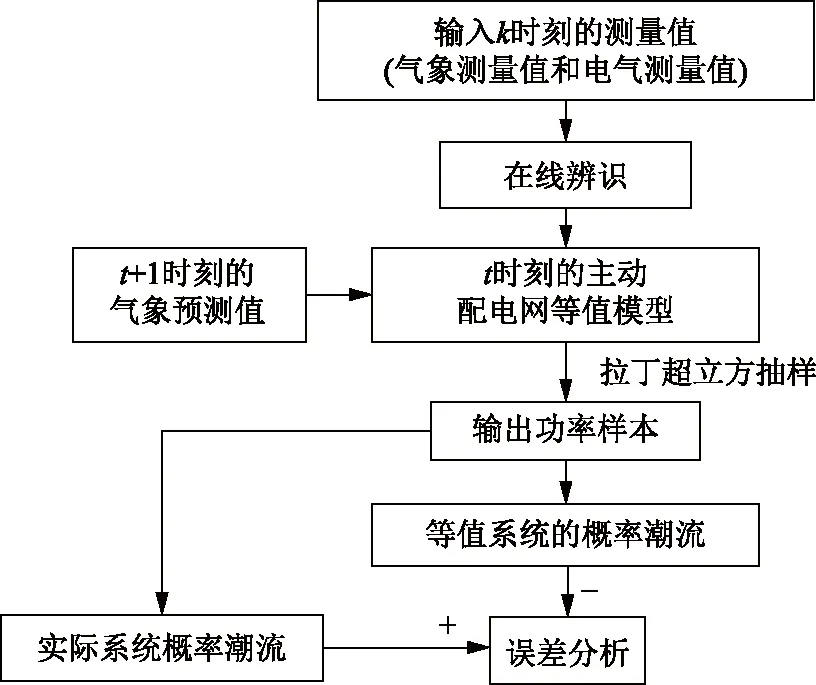
图3 等值模型精度验证流程Fig.3 Accuracy verification process of equivalent model

3 案例分析

3.1 仿真系统

本文的仿真系统是一个基于IEEE 33节点配电网和IEEE 30节点输电网的改进63节点系统[24]。IEEE 30节点输电网如图4所示。IEEE 33节点主动配电网通过一个降压变压器连接于IEEE

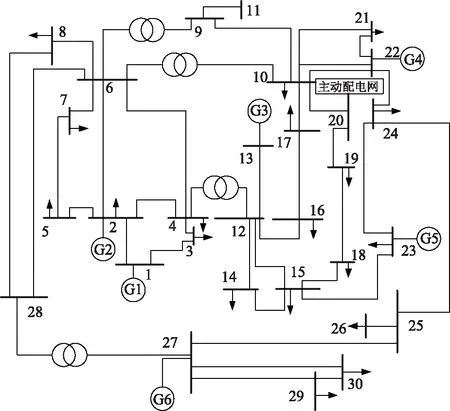
图4 IEEE 30节点输电网Fig.4 IEEE 30-bus transmission network

30节点输电网中的节点20，如图5所示。主动配电网的内部负荷设置为ZIP负荷。

测试所用的风速数据来源于国内某个风电场，光照和温度数据来源于美国国家可再生能源实验室网站。数据样本的采样间隔时间均为5 min，仿真时间为1 d(24 h)。假设IEEE 33节点主动配电网模型被图1所示的等值模型所替代，同时假设注入配电网的总功率、分布式风电总出力、分布式光伏发电总出力以及节点31的电压幅值已知。选取节点48为观测节点。

为了验证等值模型在环境发生改变情况下的精度，假设在8 h时可再生能源发电的出力发生突变。具体变化为安装在节点38、40、42、44和46上的风电机组和光伏发电系统被迫退出运行。

为了评估1 d时间内等值模型在环境变化时的精度，本文提出2个度量指标——电压指标和视在功率指标。

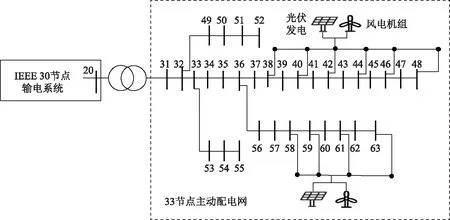
图5 IEEE 33节点主动配电网Fig.5 IEEE 33-bus active distribution network

a)电压指标

EV=|Ue-Ua|/|Ua|.

(20)

式中Ue、Ua分别为等值系统和实际系统边界电压幅值。

b)视在功率指标

ES=|UeI*e-UaI*a|/|UaI*a|.

(21)

式中I*e、I*a分别为等值系统和实际系统边界节点注入电流相量的共轭。

3.2 仿真结果

3.2.1 不同算法得到的等值模型结果

本文将IFORL算法、FORL算法和LS算法得到的辨识参数用于计算概率潮流，以验证不同算法在线辨识得到的等值模型的精度。LS算法的参数设置与文献[15]相同。FORL算法的参数设置与文献[18]相同。IFORL算法的参数设置为：α=0.5，λ=0.95，γ=0.9。3种算法下得到节点31的电压指标和视在功率指标如图6、图7所示。

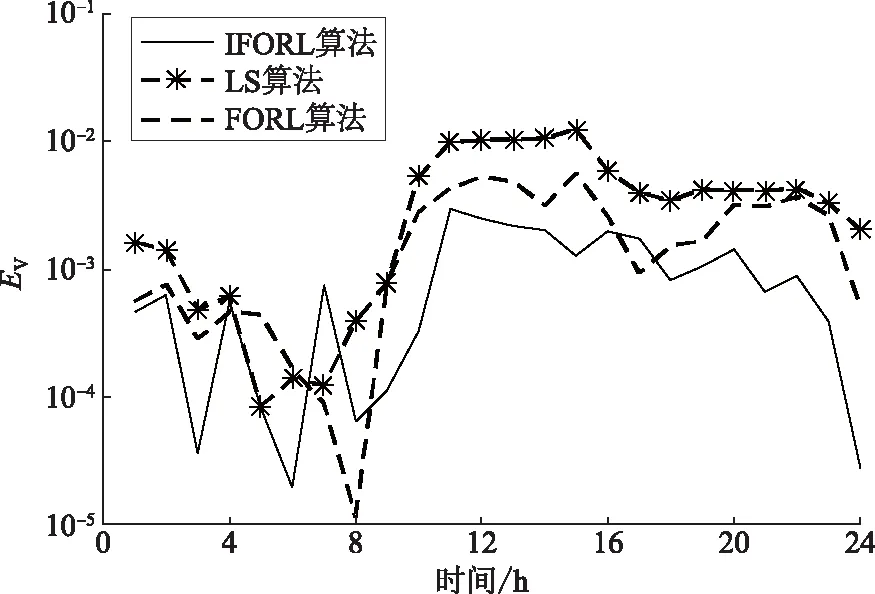
图6 不同算法下等值模型的电压指标Fig.6 Voltage indicators of equivalent model under different algorithms

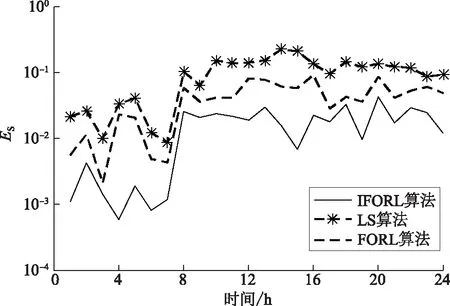
图7 不同算法下等值模型的视在功率指标Fig.7 Apparent power indicators of equivalent model under different algorithms

从图6、图7可以看出，在8 h时部分风电机组和光伏退出运行，环境状态改变，在电压指标方面，IFORL算法的误差最小，精度有一定的提升。在视在功率指标方面：IFORL算法的误差在(10-3，10-2)区间内波动，实现了在时变系统中的在线跟踪优化；FORL算法的跟踪能力较弱，由于学习速率固定，无法保证代理每次选择正确的行为，误差在(10-2，10-1)区间内波动；LS算法很难在时变环境中优化模型参数，误差达到10%，证明LS算法用于在线辨识的效果较差。

某一时刻下，配电网中不同的新能源出力波动也会影响模型输出。为了验证此时等值模型的精度，本文采用拉丁超立方抽样获得500组样本数据，并且在20 h时对等值系统中和实际系统分别进行潮流计算，获得2个系统中的边界节点电压幅值和注入视在功率的概率密度曲线，分别如图8、图9所示。

图8 实际系统和等值系统边界节点电压幅值的 概率密度曲线Fig.8 Probability density curves of boundary bus voltages of actual and equivalent systems

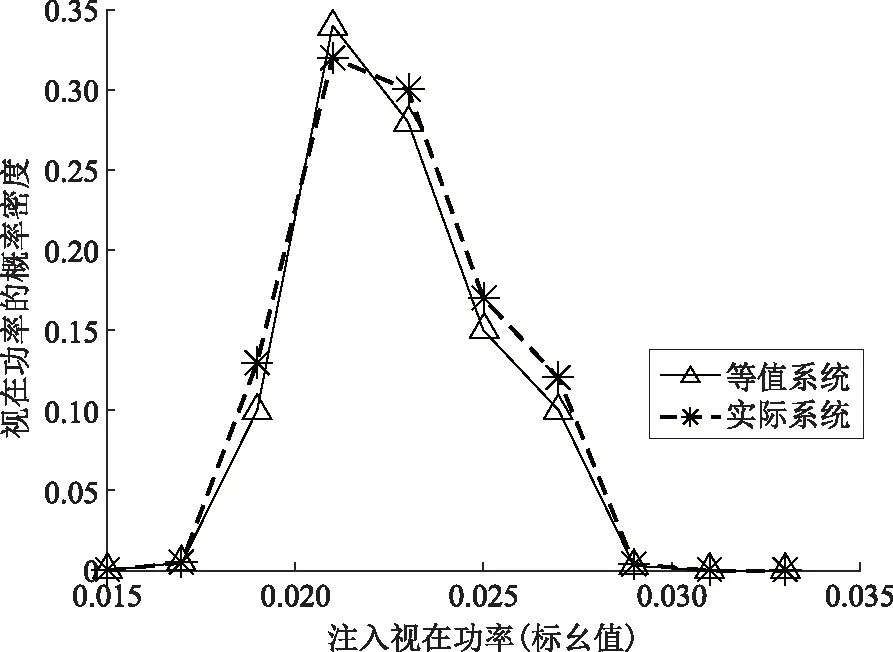
图9 实际系统和等值系统边界节点视在功率的 概率密度曲线Fig.9 Probability density curves of apparent power of boundary bus of actual and equivalent systems

从图8、图9可以看出，等值系统与实际系统的边界节点电压幅值和注入视在功率的概率密度曲线近乎重合，这证明等值模型可以完整代替IEEE 33节点的主动配电网，有效地简化了配电网，只需要知道边界节点的信息，就可以实现较高精度的配电网等值。

3.2.2 不同采样权重策略下得到的等值模型结果

为了验证本文提出的权重衰减策略获得的样本对在线辨识精度的提升效果，将其与平均权重策略进行对比。将实际的边界电压幅值和2种策略计算得到的边界节点电压幅值代入式(19)，计算得到等值模型误差，如图10所示。

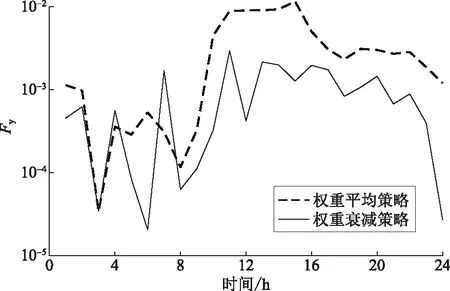
图10 不同策略下的等值模型误差Fig.10 Errors of equivalent models under different strategies

从图10可以看出：当采用权重衰减策略时，等值模型的误差在(10-4，10-3)区间内波动；在平均权重策略下，等值模型的误差在(10-3，10-2)区间内波动。这证明本文提出的权重衰减策略通过赋予当前样本较大的权重，能够使等值模型更准确地描述当前时刻的主动配电网。

4 结束语

本文建立了一种考虑源荷不确定性的主动配电网等值模型。该等值模型包括等值风电机组、等值光伏发电与等值ZIP负荷3个模块，通过IFORL算法对每个模块进行参数辨识，得到主动配电网等值模型。仿真结果表明，相比FORL算法和LS算法，引入自适应学习速率以及增加搜索方向的IFORL算法能更准确辨识环境状态改变下的样本，得到的等值模型的电压幅值和视在功率误差更小。等值模型的参数概率分布与实际系统近乎一致，表明等值模型可以有效地追踪实际系统的变化。通过不同权重策略的对比测试结果表明，本文提出的权重衰减策略通过赋予距离当前时刻较近的样本较大的权重，使等值模型的误差更小。此外，主动配电网等值模型对规模较大的配电网进行了简化，提升了潮流计算的效率，有利于短时间尺度和超短时间尺度下的系统调度和决策工作。