基于阈值的直升机飞行状态划分
李胜男, 王景霖 , 杨 乐, 邵辰彤 , 单添敏, 封锦琦
(1.故障诊断与健康管理技术航空科技重点实验室,上海 201601; 2.航空工业上海航空测控技术研究所,上海 201601;3.航空工业北京长城航空测控技术研究所,北京 101111)
直升机可适用于多方面,可用于观光娱乐、危难发生时运输物资和环境监测等;在军事领域,可用于作战、训练、运输装备等[1-2]。然而直升机在飞行中受外部气流、振动和噪声等复杂因素影响使不同飞行状态下的机动部件载荷的承载发生变化,造成机动部件损伤[3]。发生意外事故时,会造成人员伤亡及直升机的损坏等不良后果[4],因此在对直升机飞行状态划分明确的基础上,对直升机结构部件的故障诊断和寿命预测具有重要的现实意义[5-8]。
刘雨[9]提出基于支持向量机的方法进行状态划分。但在实际操作中未结合时间复杂度进行研究,实际应用中使用价值低。熊邦书等[10]采用随机森林方法实现飞行状态划分,但预分类方法准确度不高,对实际飞行状态划分结果准确性有待验证。本文采用某型直升机飞行复杂度不同的试飞数据进行飞行状态划分。采用最小二乘多项式拟合方法对直升机状态参数进行平滑处理。求取各参数数据极值,并进行差分,得到极值差分序列,以极值的差分值小于10为限定条件,考虑时间连续性,最后得到满足上述条件的对应原始数据段,划分为非转弯、平飞与稳速状态。其余采样点则为转弯、非稳速与非平飞状态。对其余偏航角、高度和速度进行差分,以差分值0为限定条件,进一步对非稳速与非平飞状态进行划分,大于0为增速,上升状态;小于0为减速,下降状态。结合发动机扭矩、主旋翼转速、俯仰角等参数阈值进行直升机37种飞行状态划分。结果表明,可对不同复杂程度的飞行数据进行状态划分,且准确率高,由于采用实际科研试飞数据进行划分,具有一定的实际工程应用价值。
1 理论基础
1.1 概率密度函数
密度函数f(x)用于描述在某个确定的取值点附近出现的概率,当求一维数据的序列概率密度函数时,函数f(x)与x所围成的面积为1,概率密度函数具有以下3种性质:
(1)
1.2 最小二乘多项式
统计学研究中,建立y=f(x)的近似表达式y=P(x),这需要从大量的实验数据(xk,yk)(k=0,1,…,m)中寻找其函数关系[11]。衡量一个函数P(x)与所给的数据(xk,yk)(k=0,1,…,m)的偏差大小,可以通过曲线拟合中常采用的偏差平方和来度量。
对于给定的数据(xk,yk)(k=0,1,…,m),在选定的函数类φ中,求P(x)∈φ,使其偏差ri=P(xi)-yi(i=0,1,…,m)的平方和最小,即
(2)
从几何上讲,所谓最小二乘曲线拟合问题,就是寻求在给定点x0,x1,…,xm处于点(x0,y0),(x1,y1),…,(xm,ym)距离平方和最小曲线y=P(x)的问题[12]。
设拟合多项式为
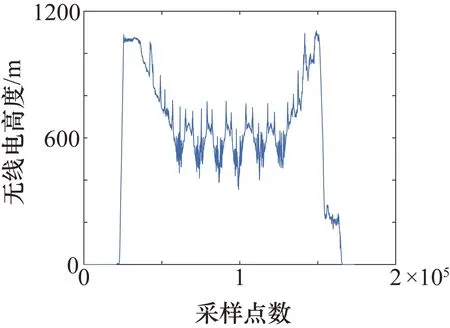
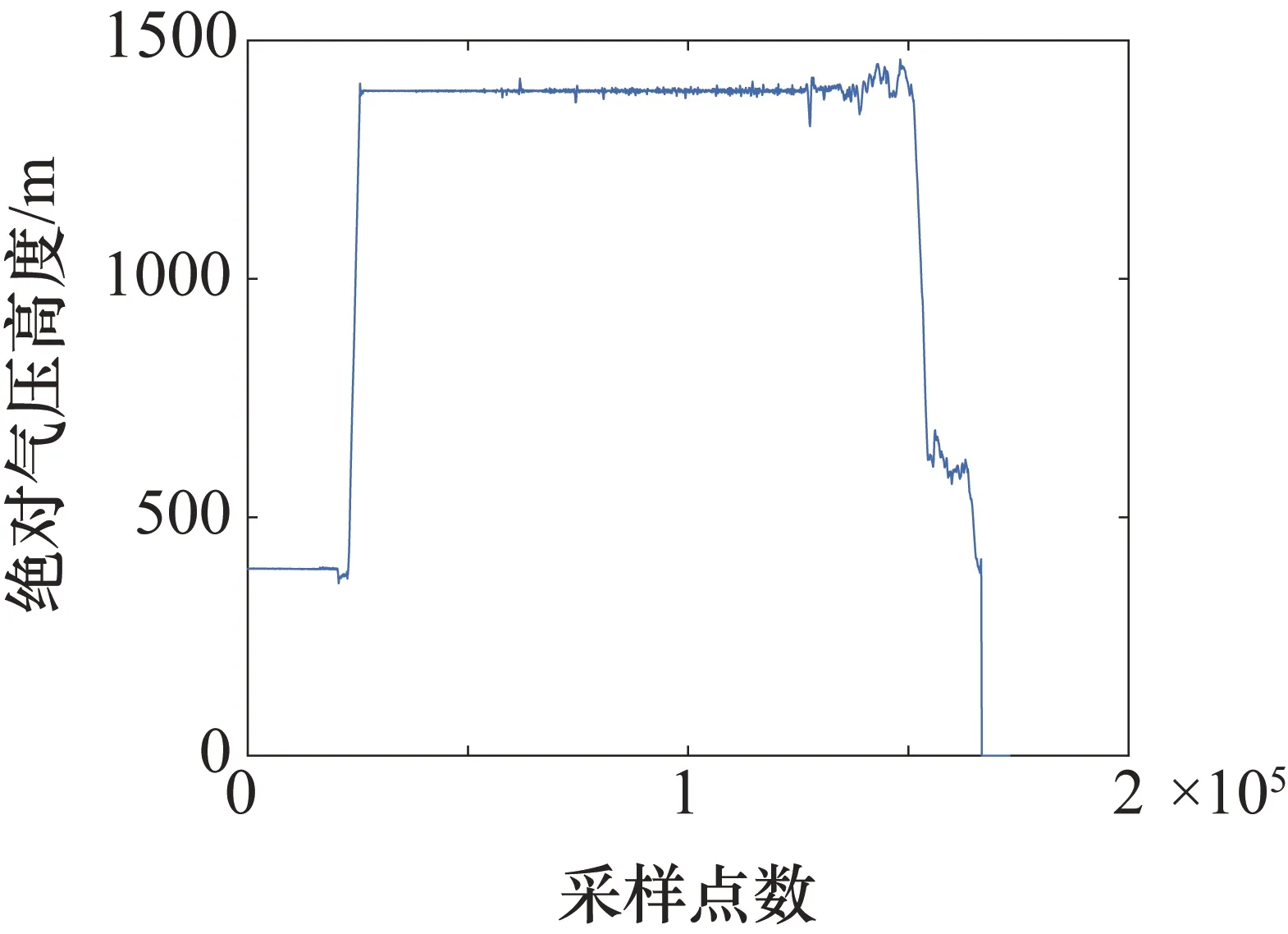
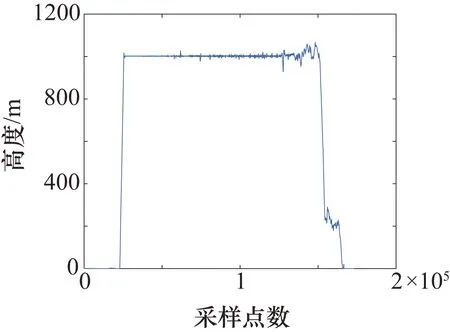
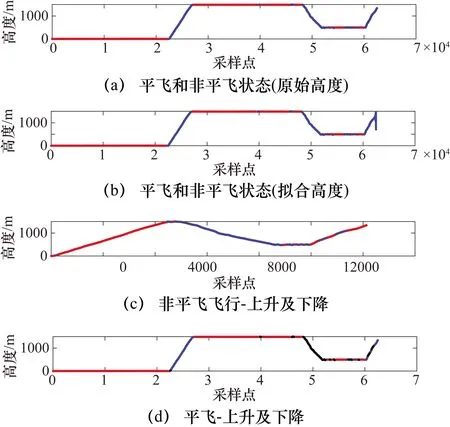
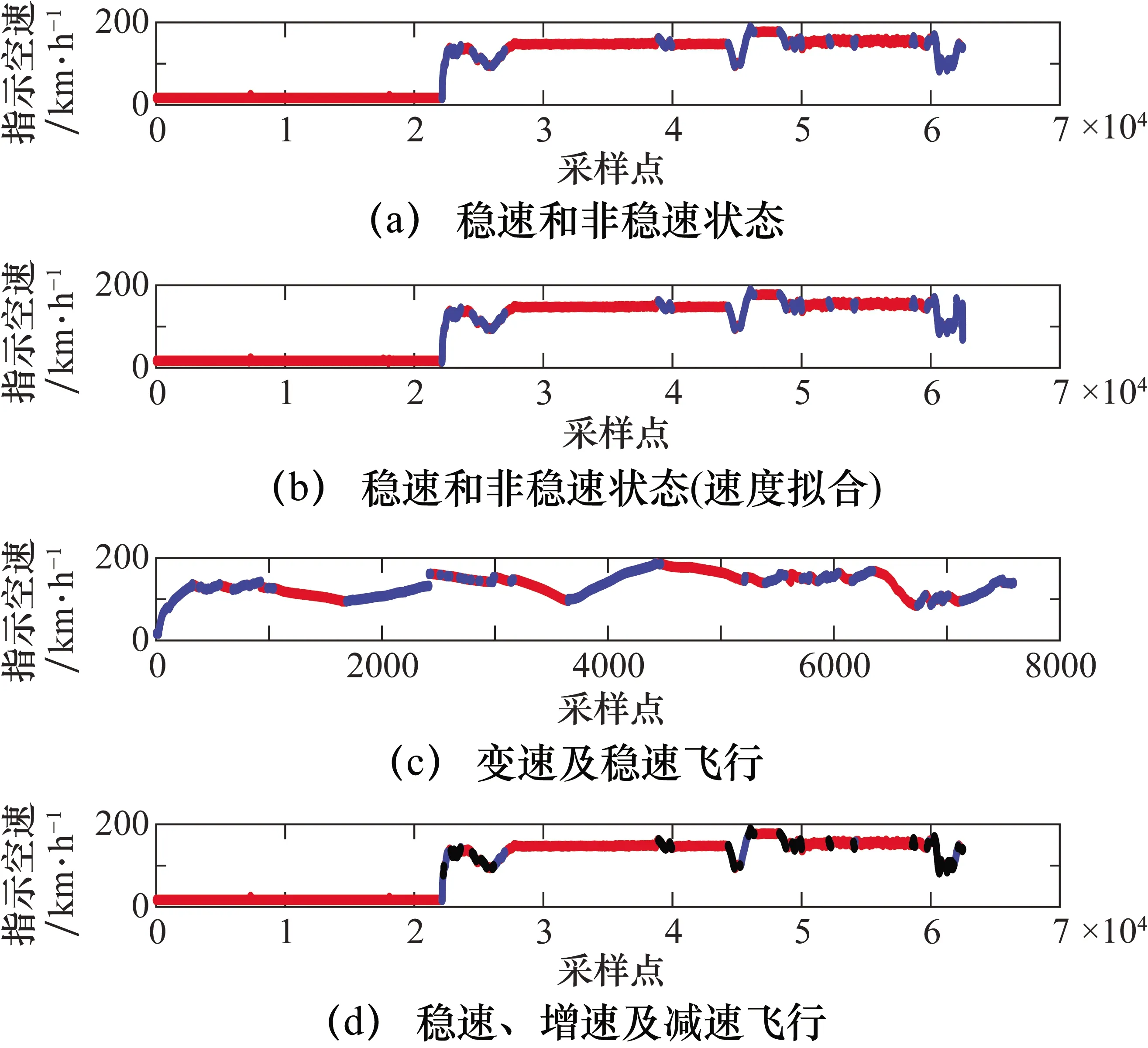
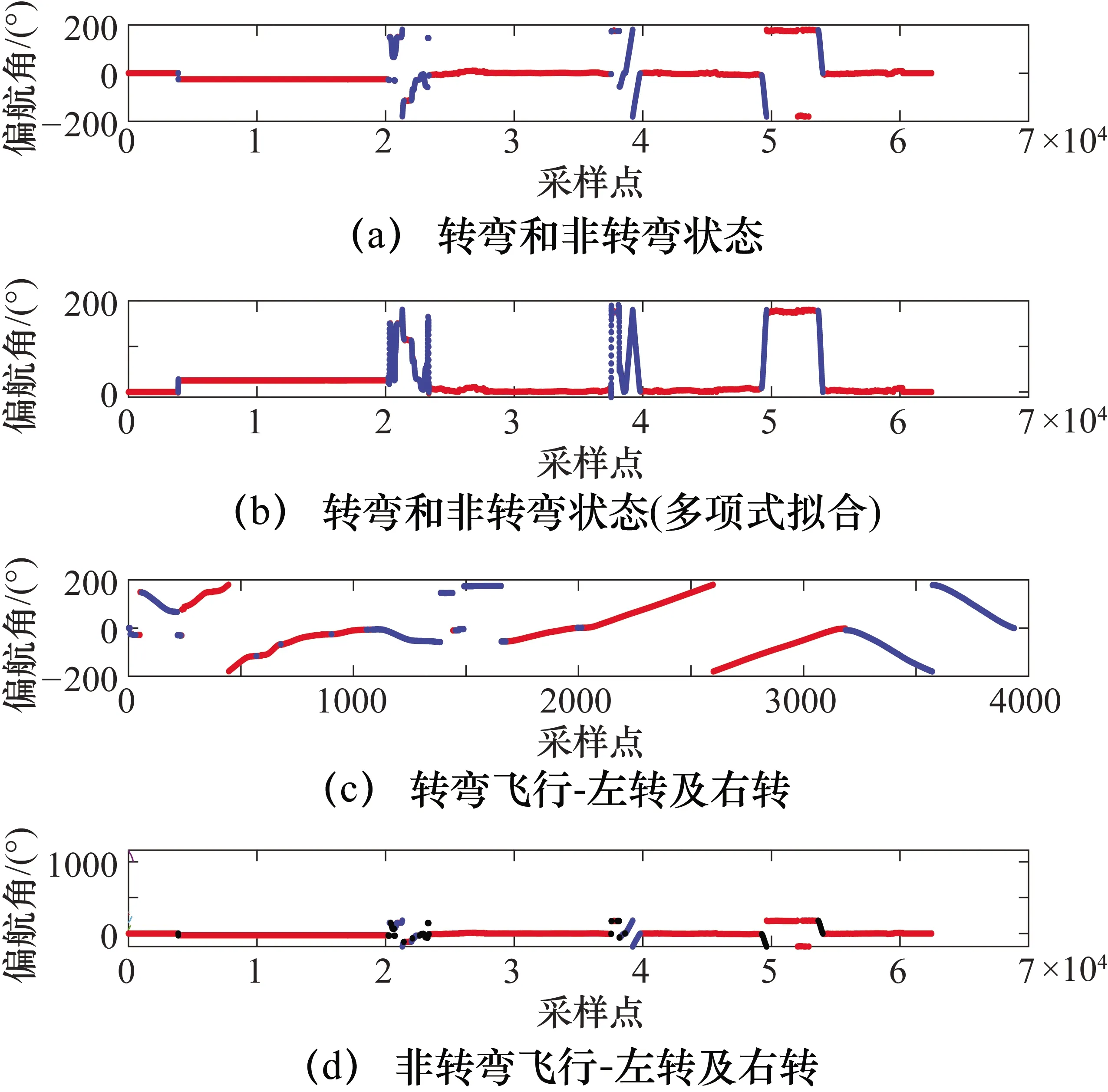
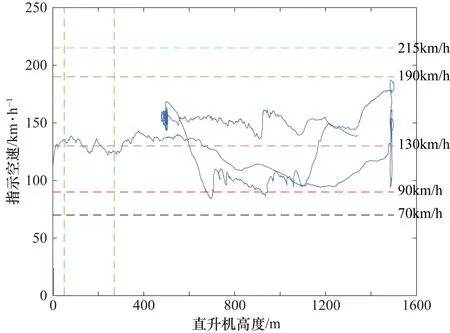
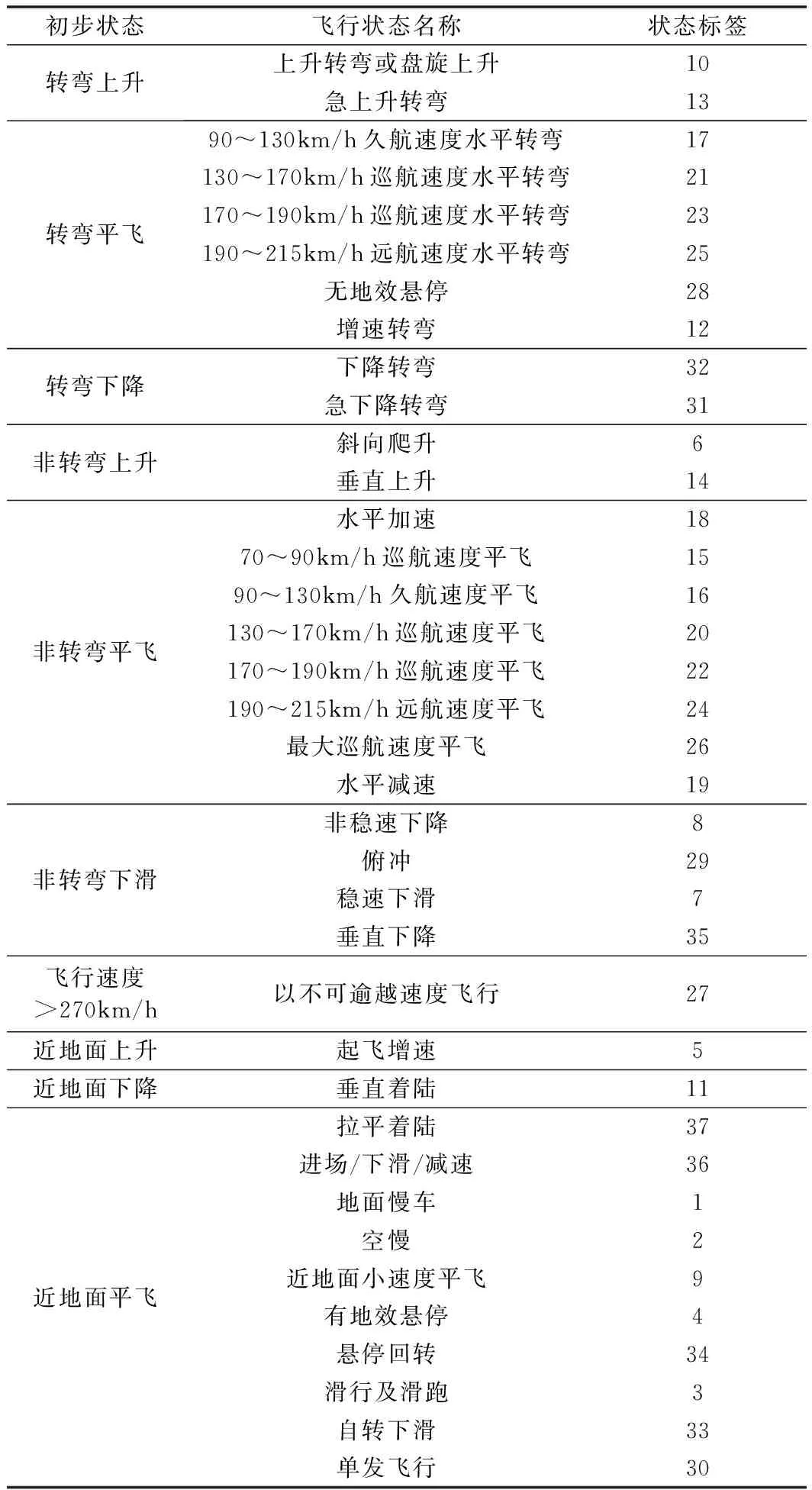
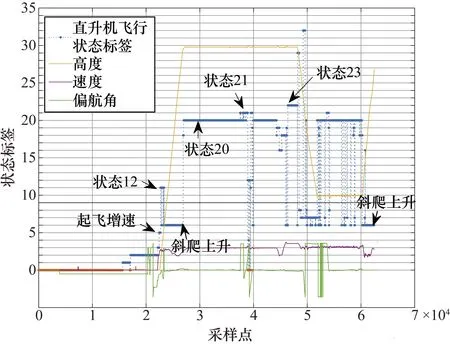
P(x)=a0+a1x+…+anxn,n (3) 通过求各项系数偏导的方法来得到结果。 首先求S(a0,a1,…,an)关于系数(a0,a1,…,an)的偏导数[13],容易得到: (4) 故使 (5) 等价为 (6) 即关于系数a0,a1,…,an的线性方程组,求解上式方程组即可得到每一项系数。 (1) 单发飞行。 当直升机脱离地面,左发动机扭矩或者右发动机扭矩中一个为0时,为直升机单发飞行状态。 (2) 自转下滑。 直升机有单相离合器,在机械结构上能够进行自转。当主旋翼系统与发动机脱开,发动机不再向主旋翼提供动力,主旋翼系统在相对气流的作用下驱动,旋翼桨叶仅由向上通过旋翼的气流来驱动,而不是由发动机动力驱动。 自转下滑是指直升机脱离地面,左发动机扭矩与右发动机扭矩同时为0且高度下降时的状态,即在连续的时间内,满足高度差分值小于或等于0。 当自转、单发飞行状态划分完后对剩下的采样点进一步进行飞行状态初步划分。在直升机科研试飞数据中,根据状态参数偏航角、指示空速、高度进行状态划分,分别将直升机初步划分为转弯非转弯、平飞非平飞、稳速及非稳速。在非平飞、非稳速过程中将状态进一步划分为高度上升与下降、增速与减速状态。 在科研试飞数据中,当高度大于1000 m时,无线电高度数据不能反映其真实飞行高度,如图1所示。 绝对气压高度参数如图2所示。其起始和着陆阶段与无线电高度数据起始和着陆阶段不一致,需要进行处理。 结合绝对气压高度数据进行处理,作为最终的直升机高度。取无线电高度小于2的采样点所在位置,找出对应位置的绝对气压高度值,求其概率密度最大值所在位置对应的绝对气压高度值记为h。 绝对气压高度值去掉h,对得到的绝对气压高度小于0的数据赋值为0,得到变化后的直升机试飞数据高度如图3所示。 图1 无线电高度图 图2 绝对气压高度图 图 3直升机高度图 直升机高度初步状态划分过程步骤如下。 ① 多项式拟合进行平滑处理。直升机高度参数数据存在波动性,采用最小二乘多项式进行拟合。具体为将高度数据按每行r个数据,变换为矩阵形式: Dn×(r+m)= (7) 分别对每行进行最小二乘多项式平滑处理,由于拟合数据的尾部存在波动性,为了消除尾部拟合数据波动的影响,每行多加m个数据进行拟合,变换后的矩阵为n行。 将高度数据变换为矩阵形式,每行r为200,为了消除末尾拟合数据波动的影响,每行多加m(m取60)个数据进行拟合,将每行拟合后的数据取前200个。每行拟合的阶次n为25时效果最佳。 ② 取极值。对经过最小二乘多项式平滑处理后的高度数据取极大值与极小值。将极大值、极小值采样点所在的位置序号按照高度原始数据采样点位置序号大小排序,得到极值点数据序列。 ③ 获得极值差分序列。对极值数据序列进行差分,得到差分值序列并在序列前补0。 ④ 平飞非平飞状态划分。考虑飞行状态的时间连续性,再根据实际高度数据序列变化特点,当高度在能够在一段时间内保持在某一稳定数值大小变化范围内,根据实际效果,若变化范围在10以内,则划分为平飞状态。即在极值差分序列中将满足至少连续两个点且极值差分序列绝对值小于10的多段极值差分序列划分为平飞范围。进一步将极值差分序列属于平飞范围的对应的原始高度数据划分为平飞状态数据,其余的高度采样点划分为非平飞状态数据。 ⑤ 直升机上升与下降初步状态划分。对于非平飞数据进行上升与下降状态划分。对步骤④的非平飞高度数据进行差分,差分值大于0的差分值所在位置对应的高度数据划分为上升状态,则其余的为下降状态数据。原始高度与拟合高度划分的上升、平飞与下降状态如图4所示。 图4 直升机原始高度与拟合高度划分的上升、平飞与下降状态图 图4(a)中,蓝色线段为非平飞,红色线段为平飞;图4(b)为图4(a)的平滑处理结果;图4(c)中,蓝色线段为高度下降,红色线段为高度上升;图4(d)中,蓝色线段为高度上升,红色线段为平飞,黑色线段为高度下降。 按照步骤①~步骤⑤划分过程,得到直升机速度与偏航角的初步状态划分结果如图5、图6所示。 图5 直升机稳速、增速与减速状态图 图6 直升机非转弯、左转及右转状态图 图5(a)中,蓝色线段为变速,红色线段为稳速。图5(b)为图5(a)的平滑处理结果;图5(c)中,蓝色线段为增速,红色线段为减速;图5(d)中,蓝色线段为增速,红色线段为稳速,黑色线段为减速。 图7可直观地反映此架次飞行的整体情况。图7中近地面阈值为50 m,高低空阈值为270 m。根据速度阈值将速度划分为不同范围:过度速度70~90 km/h;久航速度90~130 km/h;久航速度与远航速度之间130~190 km/h;远航速度190~215 km/h。巡航速度130~190 km/h划分为两个速度范围,分别为130~170 km/h和170~190 km/h。 某直升机总采样点数为77334个,每13个采样点为1 s,根据状态参数阈值并按以下规则将直升机划分为37个飞行状态如表1所示。 图7 直升机速度高度图 表1 飞行状态划分 图6(a)中,蓝色线段为转弯,红色线段为非转弯;图6(b)为图6(a)的平滑处理结果;图6(c)中,蓝色线段为右转,红色线段为左转;图6(d)中,蓝色线段为左转,红色线段为非转弯,黑色线段为右转。 在表1的飞行状态划分中,首先在2.2节的初步状态划分及阈值基础上得到第一列,再根据高度、速度阈值直接划分出32种状态,其中悬停、地面慢车、空慢、急上升和下降转弯及拉平着陆过程划分的参数阈值具体如下。 ① 悬停:当直升机脱离地面,保持高度不变,没有发生转弯,即偏航角和高度为固定值、速度约为0时为悬停状态。 ② 地面慢车:当主旋翼转速为127~129 r/min时,且直升机未离开地面,速度约为0时,为地面慢车。 ③ 空慢:当主旋翼转速大于240 r/min时,且直升机未离开地面速度约为0时,为空慢。 ④ 急上升和下降转弯:根据实际效果,当直升机处于转弯、上升飞行状态,且高度差分值大于5 m时为急上升转弯状态,当直升机处于转弯、下降飞行状态,且高度差分值大于5 m时为急下降转弯状态。 ⑤ 拉平着陆:当直升机在高度下降着陆过程中时,俯仰角单调增大且时间连续4~8 s,则划分为拉平着陆状态。 按照以上规则进行直升机37种飞行状态划分得到第47架次飞行过程中飞行状态的变化情况,如图8所示。 图8 直升机飞行状态划分结果 图8中,蓝色线段为直升机对应的飞行状态。在此次飞行架次中并非完整记录直升机从起飞到着陆过程,而是记录从起飞到飞行的过程,因此并未出现飞行状态36、37。 在得到的直升机飞行状态划分结果中,将直升机高度、速度、偏航角按一定比例缩放到同一幅图中,并对高度、速度、偏航角进行条件限定,进行准确率识别,过程如下。 ① 直升机飞行状态划分后得到每个采样点对应的状态标签,不同时间段可能出现同一种飞行状态,因此将飞行状态标签按照在某段时间内为同一种标签划分为多段。 ② 找出每一段状态标签对应的原始数据采样点序号中对应的高度、指示空速、偏航角,根据不同状态与对应的限定条件进行判断。当此段数据中对应的偏航角标准差、指示空速标准差、高度标准差小于1时,为非转弯、平飞、稳速,否则为转弯、非平飞、非稳速。 ③ 列出分段后的不符合对应状态判定标准的每段的采样起始点和终止点。 将直升机划分的各采样点编号与对应的实际飞行状态结果进行对比,划分错误的采样点如表2所示。 表2 飞行状态划分准确率分析 从表2中可知,划分错误采样点个数为728个。其中,直升机为未启动状态(即0状态,不属于任意一种飞行状态)采样点个数为16207个。最终得到的直升机飞行状态划分的准确率为 采用最小二乘多项式拟合方法分别对偏航角、高度、指示空速进行平滑处理。求取各参数数据极值,以参数数据极值的差分值小于10为限定条件,得到对应的原始数据段划分为非转弯、平飞和稳速状态,其余采样点则为转弯、非稳速和非平飞状态。以参数差分值0为限定条件,进一步对非稳速与非平飞状态进行划分,最后结合发动机扭矩、主旋翼转速、俯仰角等参数阈值进行直升机37种飞行状态划分。划分结果与实际状态进行对比,得到划分准确率达到98.34%,相比预分类方法进行飞行状态划分准确性不确定的问题,此方法实用性强,可对飞行复杂程度不同的直升机进行飞行状态划分,具有很高的准确率。存在划分错误其主要原因是状态参数数据波动较大,经过多项式拟合进行平滑处理后,仍存在较大波动,且多项式拟合存在一定的误差。2 直升机状态分类
2.1 直升机悬停、单发飞行及自转状态分类
2.2 直升机初步状态分类
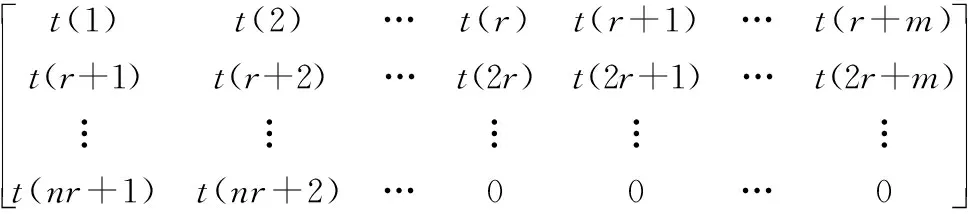
2.3 直升机状态划分规则
3 直升机状态划分准确率分析

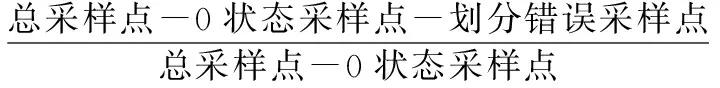
4 结束语

