机载燃油流量电磁转动测量方法研究

徐 伟， 林 波， 刘兆强， 江文波， 张思宇， 胡 敏

(四川泛华航空仪表电器有限公司，四川 成都 610500)

在军用航空飞机的机载系统中，燃油测量是非常重要的功能之一[1]。通过测量油箱内剩余燃油量和机身油箱向外实时输送的燃油量判断飞机的飞行状态和续航里程，为驾驶员在飞机的起降、加速与减速、判断作战半径的过程中提供精确的信息指示[2-3]。其中实时燃油耗量的测量主要依靠前端流量传感器采集数据并在后端电路转换处理为可用电信号，但由于军用飞机在飞行过程中的环境气候、飞行高度、工作温度、飞行速度等工况都存在较大的变化，增加了流量传感器精确测量输油管中流过油量的难度，并对其设计方案的优化提出了更高的要求。

目前，各种新兴的检测技术在液体或气体流量测量领域得到了广泛的研究和应用，根据物理原理可分为电磁法[4]、超声法[5]和涡流法[6]。对于军用飞机而言，其燃油流量测控系统需要多考虑在复杂条件下的稳定性和精确性，因此目前主要依据电磁原理设计，通过不同的传感器结构将燃油管中的流量转化为某电磁参数的变化以实现测量功能[7-8]。现在国内外应用较为普遍的电磁流量传感器根据其信号转换的原理可分为：① 磁铁随叶轮旋转导致外围线圈中产生感应电压；② 叶轮旋转扰乱外围磁铁产生的磁场，从而在磁铁上方的线圈中产生感应电压；③ 铁磁性材料的部件随叶轮旋转导致外围工字形通电线圈中的电感发生改变，使其中电压信号随之变化。在实际应用时，具体选用何种方法需要根据应用环境和主机所提出的技术要求确定[1]。

在已有技术的基础上，针对第一种电磁转动测量方法简易可行但输出的感应电压信号较弱的特点，提出运用有限元仿真方法，正向设计流量电磁测量系统模型，分析磁源分布方式、感应线圈结构、叶轮转速、传感器材料等参数对线圈中电压曲线的影响，以较少的研发成本得到最优的设计方案，使流量测量结果更为准确，提升燃油流量测量系统的可靠性。

1 方法原理

1.1 流量电磁转动测量模型

根据电磁转换原理测量燃油流量的方法是将传感器叶轮安装在供油管路中，流过管路的燃油冲击叶轮，使其按预定方向旋转，将燃油流量大小转换为叶轮转速。在叶轮转动过程中，与其同轴且位于叶轮内部的磁铁组随之转动，在转动过程中向外扩散的磁场曲线导致外围线圈中磁通量规律性变化，从而产生感应电压，检测该感应电压的幅值特征与频率特征，结合在设计叶轮结构时确定的管内流量与叶轮转速的对应关系，即可实现燃油流量的实时测量。图1为电磁流量传感器的结构示意图。

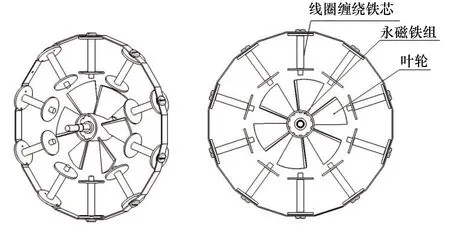
图1 流量传感器结构示意图

1.2 理论推导

磁铁是一种具有宽磁滞回线、高矫顽力、高剩磁，一经磁化即能保持恒定磁性的材料。将多组磁铁均匀安装在流量传感器轴上，使其在随叶轮旋转的过程中不断激发磁场曲线致使外围线圈中产生感应电压。磁铁作为稳定磁源，在计算其空间磁场时可将其视为一种等效电流模型[9]，磁铁的磁性等效于沿侧表面的大环形电流，对于磁化强度为M的磁铁，其等效电流密度为

Js=M×n

(1)

式中，n为磁铁表面外法线单位矢量。

对于均匀磁化的磁铁，假设其磁化方向为z向，磁化强度为M，根据等效电流密度Js，得到等效电流I=Js·h。取平行于xy平面的任一厚度为Δz0的截面，分析等效的薄层电流环在外部空间一定距离处的磁场dB。磁铁等效电流计算模型如图2所示。

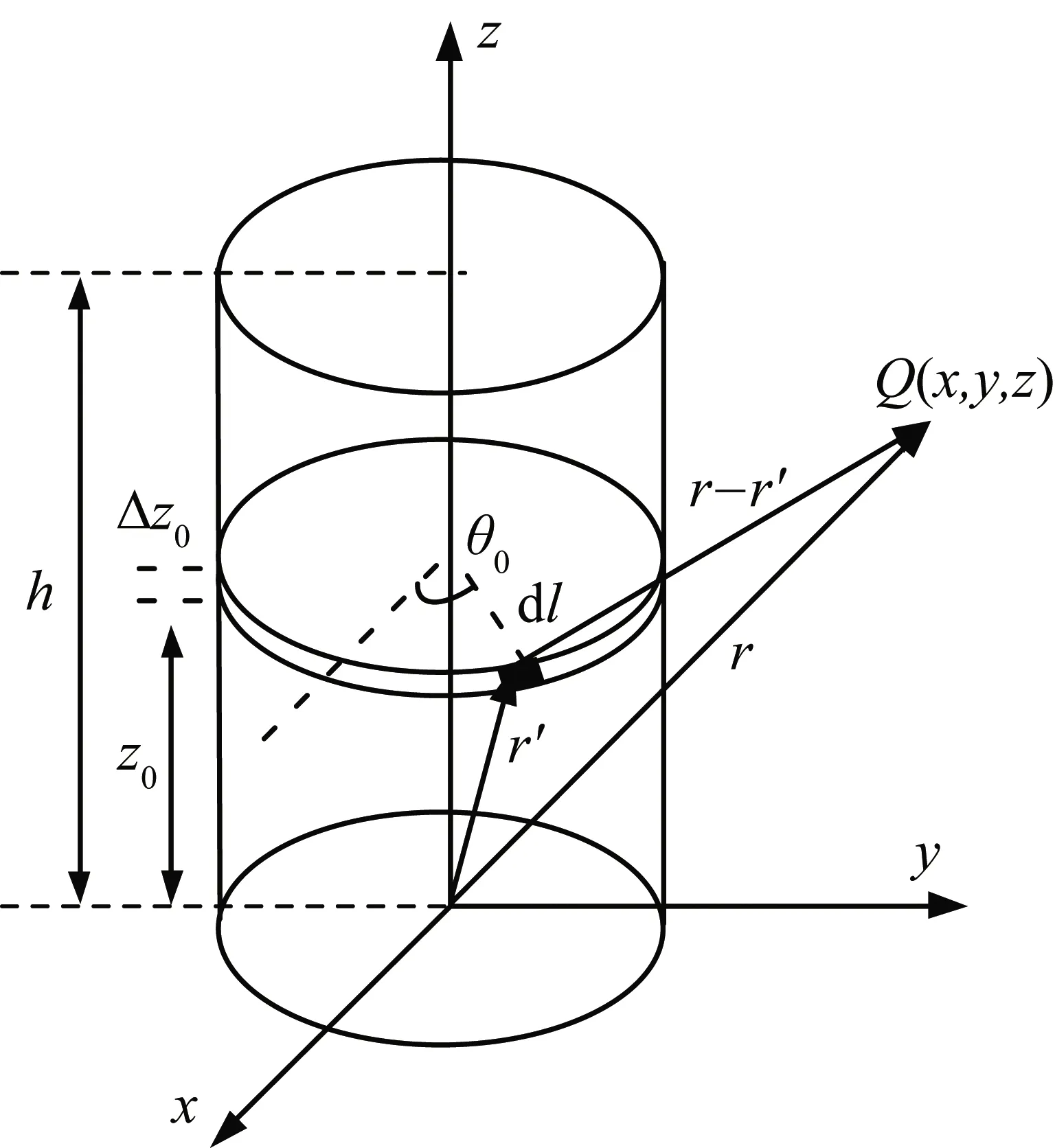
图2 磁铁等效电流计算模型

根据毕奥-萨伐尔定律，该薄层电流环在Q(x,y,z)点产生的磁场强度[10]为

(2)

对于薄层电流环上任一小段Jsdl，在圆柱坐标系下，假设其位置为(acosθ0,asinθ0,z0)，对式(1)进行如下变换:

=M·(-asinθ0i+acosθ0j+0k)dθ0dz

(3)

r-r′=(r·cosθ-a·cosθ)i+(r·sinθ-a·sinθ)j+(z-z0)k

(4)

(5)

(6)

由此可知，薄层电流环在Q(x,y,z)点处的磁场强度dB为

dB=

(7)

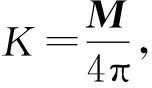
(8)

(9)

(10)

对比上述公式可知，空间磁场强度与磁铁几何尺寸、空间位置、磁化强度有关。

如图3所示，当磁铁逆时针转动时，左边线圈中向上扩散的磁通量增加，根据法拉第电磁感应定律和楞次定律，线圈中产生的感应电流总是要用自己激发的磁场来阻碍引起感应电流的磁通量变化，因此左边线圈中产生的感应电流为顺时针方向，同理可得中间线圈和右边线圈中磁通量的变化情况和产生的感应电流方向。为使各组线圈相连时电流方向相同，应将左边与中间线圈尾尾连接，中间与右边线圈首首连接，多组线圈时以此规律交错相连[11]。

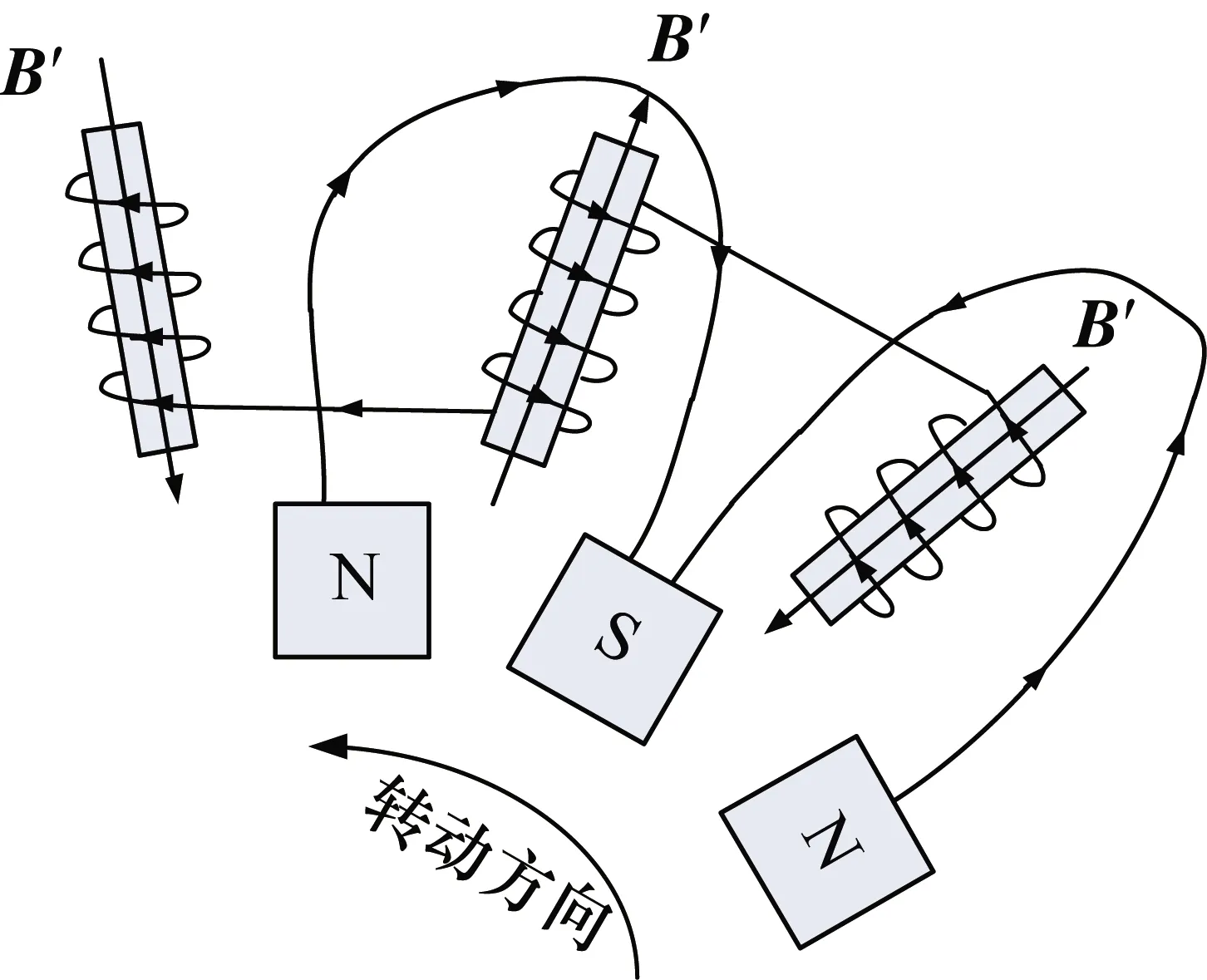
图3 线圈感应电压产生原理示意图

在得到磁铁在空间中产生的磁场大小的计算方法后，进一步根据法拉第电磁感应定律得到线圈中的感应电动势：

(11)

式中，E的大小与φ和Δφ的大小无必然联系，与φ的变化率成反比关系，且E的大小与线圈匝数n紧密相关。

2 模型仿真分析

2.1 模型表征方法

对于目前大部分的军用飞机，燃油流量传感器中使用的叶轮一般由铝合金材料制造，使其在满足结构强度的基础上减少产品质量[1，9-12]。查阅资料可知，铝合金材料的相对磁导率约等于空气磁导率[13]，且图1所示模型近似为前后对称结构，因此可将流量传感器实物模型在有限元仿真中简化，如图4所示。

图4 流量传感器有限元仿真模型

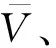
由图5(a)可知，当磁铁随着叶轮一起转动，其产生的磁场曲线构成闭合回路，主要集中在磁铁附近，且磁场强度随着距离的增加急剧减小。由图5(b)可知，在基础模型参数条件下，仿真得到的线圈感应电压曲线形态平滑，电压幅值为16 mV，电压频率为叶轮每转1圈产生5个周期信号。

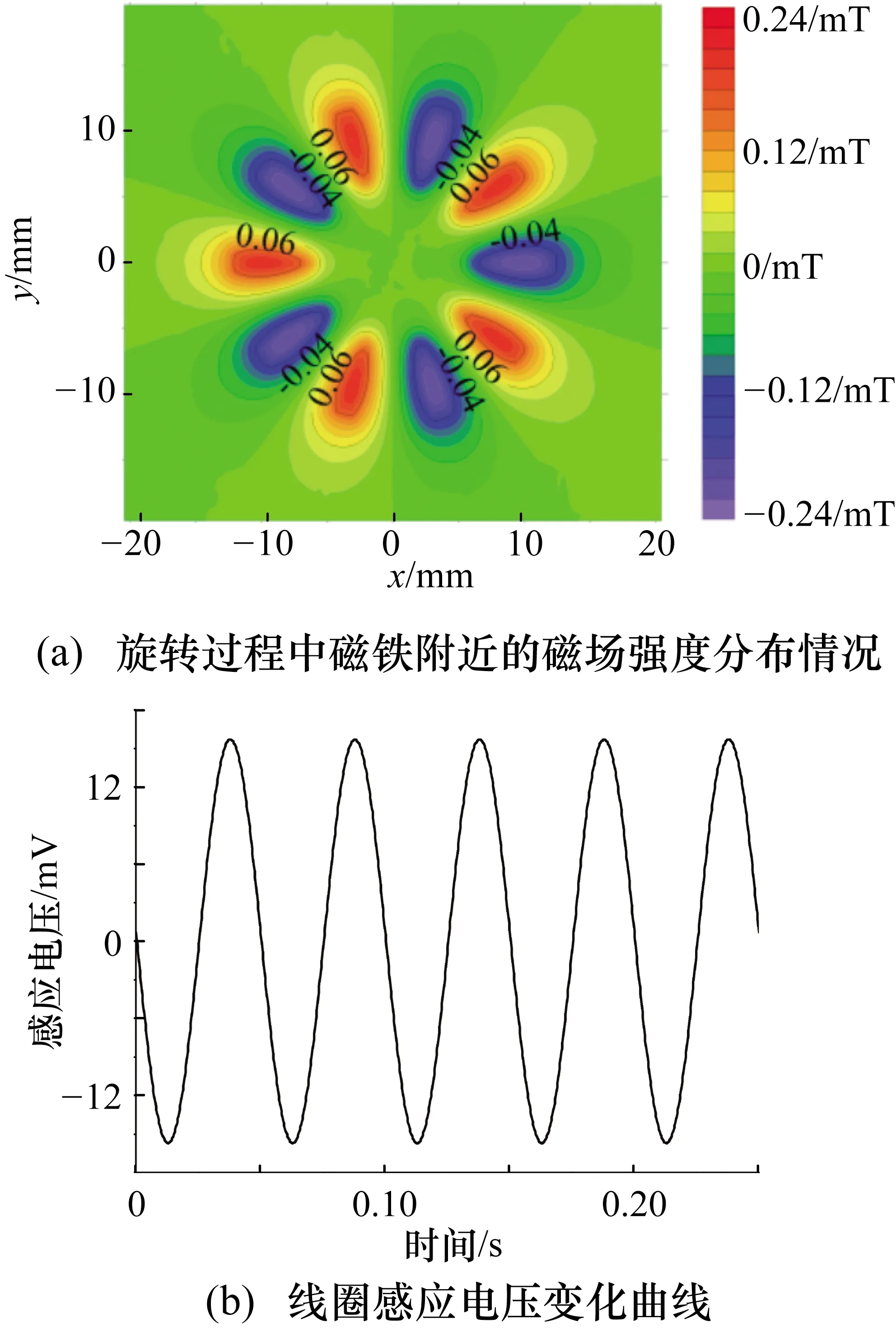
图5 基础模型参数下得到的仿真结果

2.2 影响因素分析

2.2.1 磁铁与线圈距离影响

受制于在飞机中的应用环境，流量传感器的外观和整体尺寸是基本不变的，为了分析磁铁与线圈之间的距离D2对感应电压幅值特征的影响，保持原模型中其他参数不变，以2 mm为取值间隔，分析D2值从40 mm递减到34 mm时感应电压的幅值变化情况，所得仿真结果如图6所示。

由图6可知，当磁铁与线圈之间的距离增大时，感应电压幅值逐渐减小，且对于相同的距离改变量，磁铁越靠近线圈，对线圈中电压幅值的影响越明显，该规律与永磁铁激发磁场在空间中的衰减特性相同。

2.2.2 铁芯相对磁导率影响

作为流量传感器内部具有导磁效应的部件，线圈中感应电压的大小与铁芯内部磁感应线强度紧密相关。为分析不同材料铁芯的使用效果，在有限元仿真模型中使用相对磁导率进行表征，令μ值从50～200间隔50取值，得到的线圈感应电压幅值变化情况如图7所示。

由图7可知，当铁芯的相对磁导率由50逐渐增大至200时，线圈中产生的感应电压幅值变化较小，集中在15～17.5 mV。且由图7(b)可知当磁导率逐渐增大时，电压幅值的增量逐渐减小，说明在该模型参数条件下，铁芯相对磁导率的变化对感应电压的影响较小。分析其原因如下：在同样的磁场环境条件下，不同的铁磁性材料的磁化效果都是有限的，因此当相对磁导率超过一定范围后，对感应电压的影响逐渐减弱。

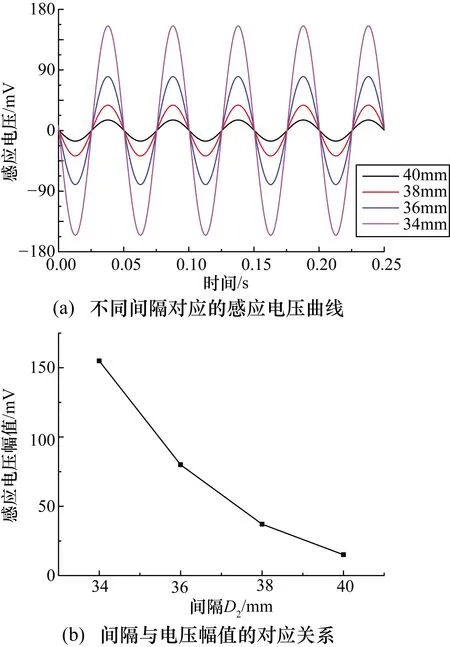
图6 间隔D2对线圈感应电压的影响

图7 铁芯磁导率对线圈感应电压的影响

2.2.3 磁铁剩磁强度影响

磁铁作为流量传感器中的信号激励源，分析其本身的磁场强度对线圈感应电压的影响具有重要的意义。假设常规流量传感器中所使用的磁铁可充磁范围较大，在仿真模型中令其剩磁值从0.1～0.9 T间隔0.2 T均匀变化，所得仿真结果如图8所示。

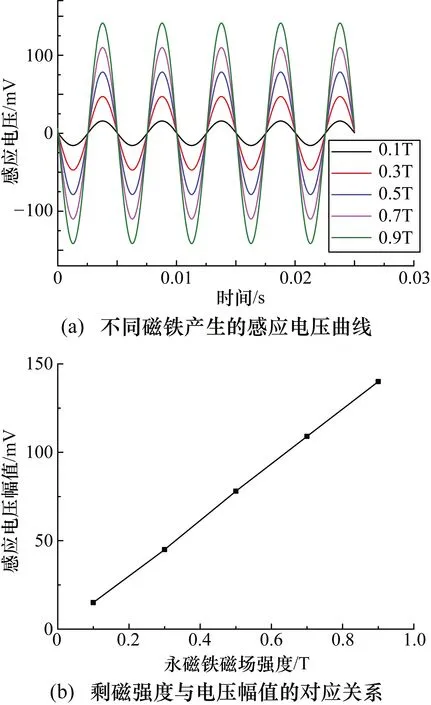
图8 磁铁剩磁强度对线圈感应电压的影响

由图8可知，当磁铁剩磁强度在0.1～0.9 T范围内线性增加时，其对线圈感应电压产生的影响也呈线性变化趋势，电压幅值从16 mV逐渐增大至149 mV。仿真结果表明在磁铁材料的可充磁范围内，适当增大其剩磁强度有利于线圈中感应电压的检测。

2.2.4 叶轮转速影响

在军用飞机的战斗过程中，不同的飞行状态下燃油管中流过的燃油量是不同的，对应的叶轮转速随之实时变化，因此流量传感器在设计时需要充分考虑在全检测流量范围内的可用性。为了保证在低流量和高流量时传感器都能稳定工作，需要对叶轮转速和感应电压幅值之间的关系进行分析，明确其影响效果以便指导在不同工作条件下的传感器优化设计。根据飞机燃油管中流速的常见范围，假设叶轮转速分别为2 r/s，4 r/s，6 r/s，8 r/s，10 r/s，多次仿真后得到的感应电压曲线如图9所示。

由图9可知，随着叶轮转速的改变，感应电压的幅值及单位时间内可检测的信号脉冲数都是随之变化的。当叶轮转速由2 r/s变化为10 r/s时，感应电压幅值逐渐增大，且该变化趋势近似为线性关系；单位时间内可检测的信号脉冲数也逐渐增加，具体个数整理如表1所示。

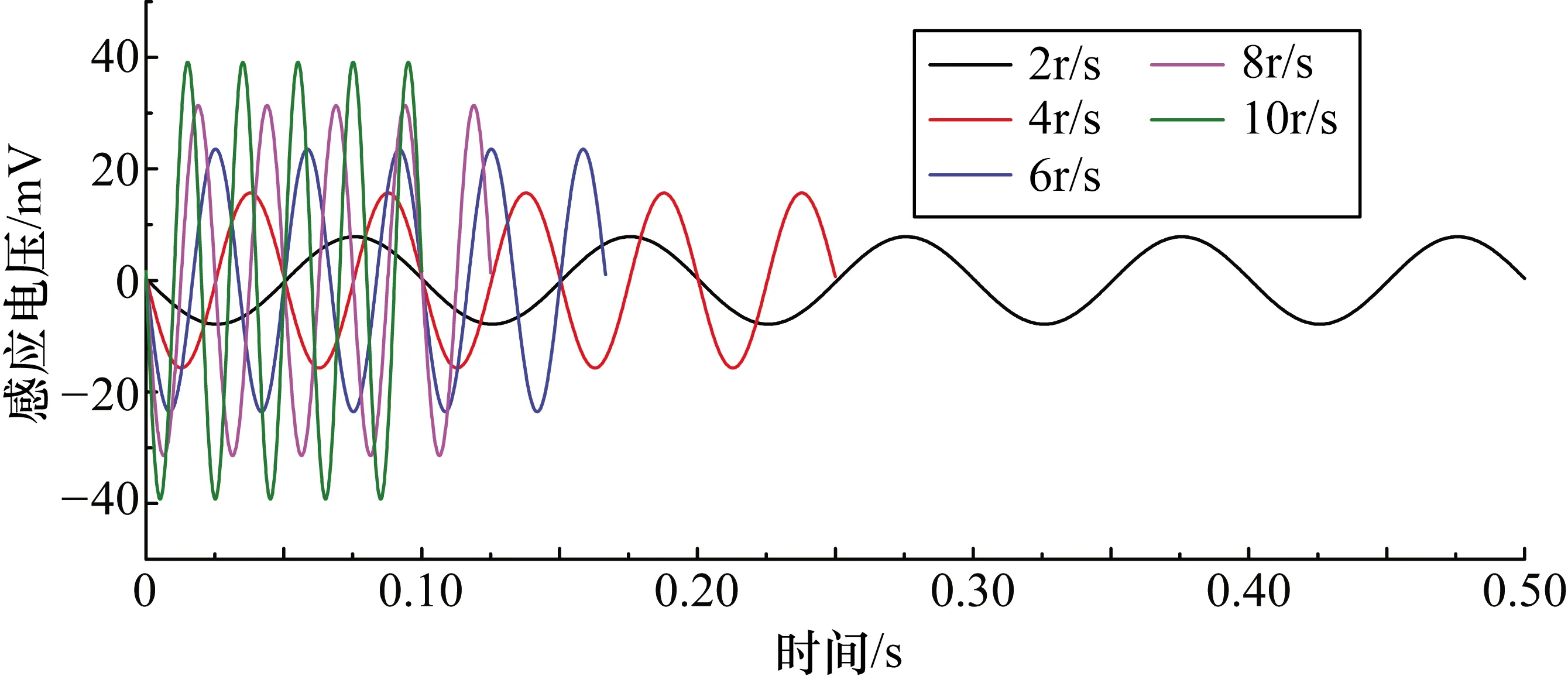
图9 叶轮转速对线圈感应电压的影响

表1 不同叶轮转速对应的感应电压曲线特征

3 不同N1与N2的组合分析

由上述分析可知，在10组线圈和10组磁铁的情况下，感应电压的曲线基本满足正弦函数关系，与理论结果相符。对于其他的线圈与磁铁组合方式，分析其产生的感应电压曲线是否满足要求也可采用有限元方法进行正向验证，减少不必要的制造成本。对于线圈数和磁铁数相等的模型，取其值为4和6，仿真结果如图10和图11所示，其中图10(a)和图11(a)为磁铁附近的磁场强度分布，图10(b)和图11(b)为线圈中感应电压曲线。对于线圈数和磁铁数不相等的模型，取磁铁数为6，线圈数为4和10，仿真结果如图12所示。

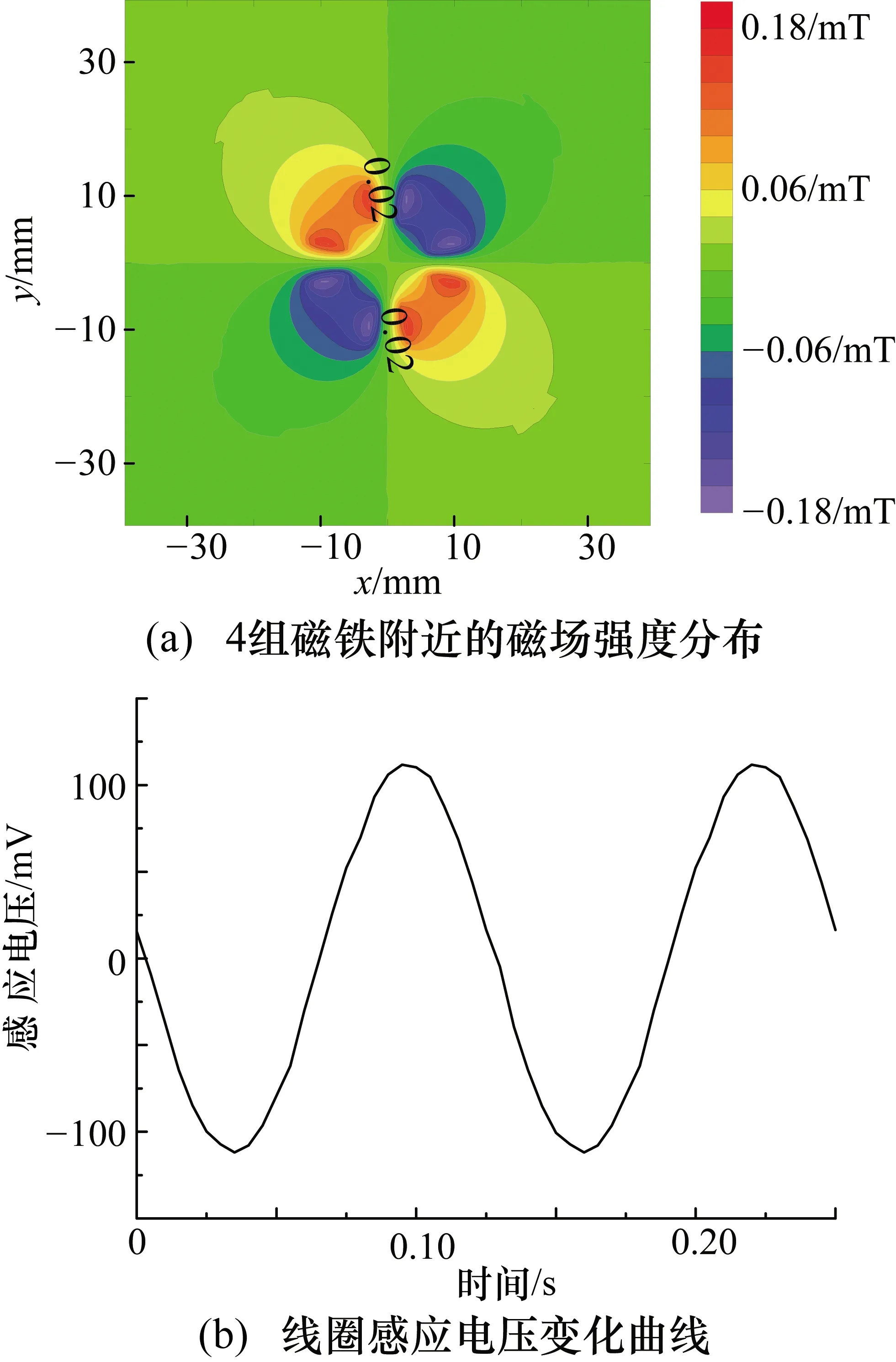
图10 4组线圈和4组磁铁对应的仿真结果

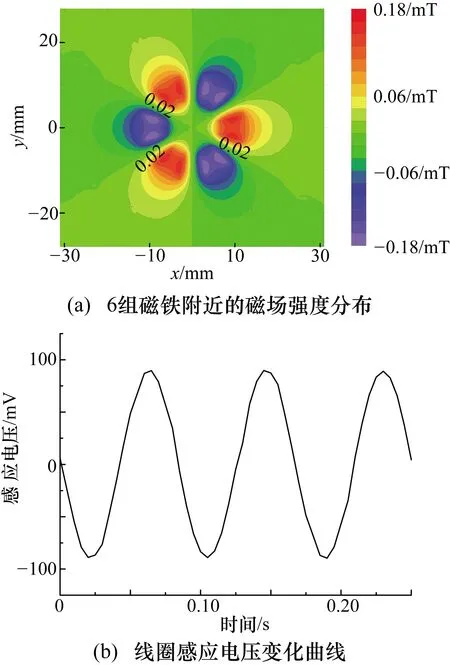
图11 6组线圈和6组磁铁对应的仿真结果

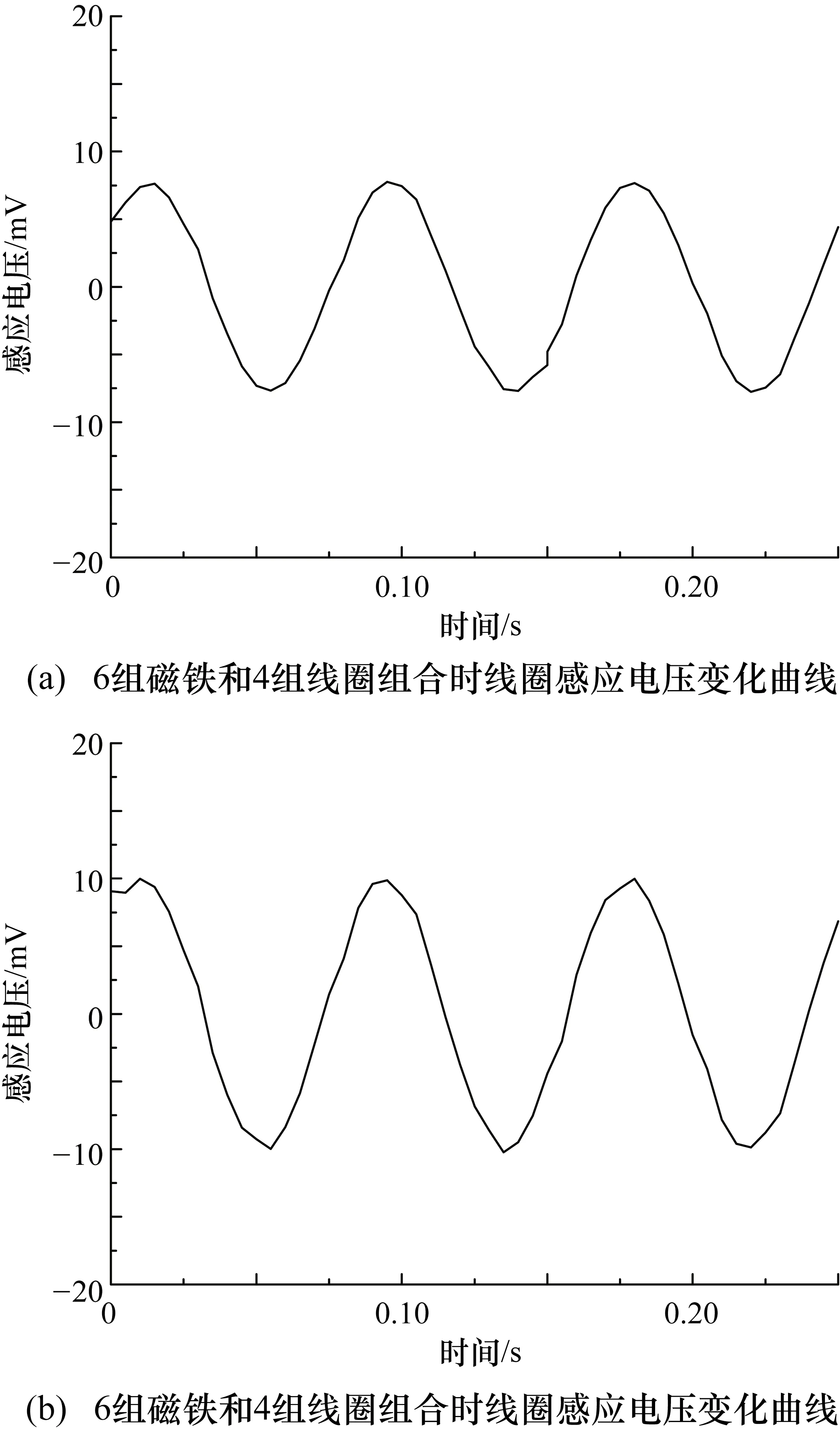
图12 磁铁与线圈数不等时的仿真结果

由图10和图11的对比可知，当流量传感器中线圈数与磁铁数相等时，4组产生的感应电压幅值略大于6组产生的感应电压幅值，且均远远超过图5中所示的10组产生的感应电压。由图12可知，当线圈数与磁铁数不等时，无论6组磁铁对应4组线圈或10组线圈，其产生的感应电压幅值均小于10 mV，且电压曲线的平顺程度不及组数相等时得到的结果。综合上述分析可知，在设计传感器内部磁铁和线圈结构时，应注意保持其组数相同，绕圆周呈均匀分布且适当减少组数。

4 实验验证

在上述仿真模拟的基础上，为验证结果的正确性，分别完成了6组磁铁对应6组线圈和10组磁铁对应10组线圈的等效实验，实验装置的示意图如图13所示。实验中使用的流量传感器参数为D1=25 mm，D2=44 mm，μ=20，Br=1 T，n=24000，叶轮转速分别为33 r/s和11 r/s，实验得到的感应电压幅值和频率如表2所示。

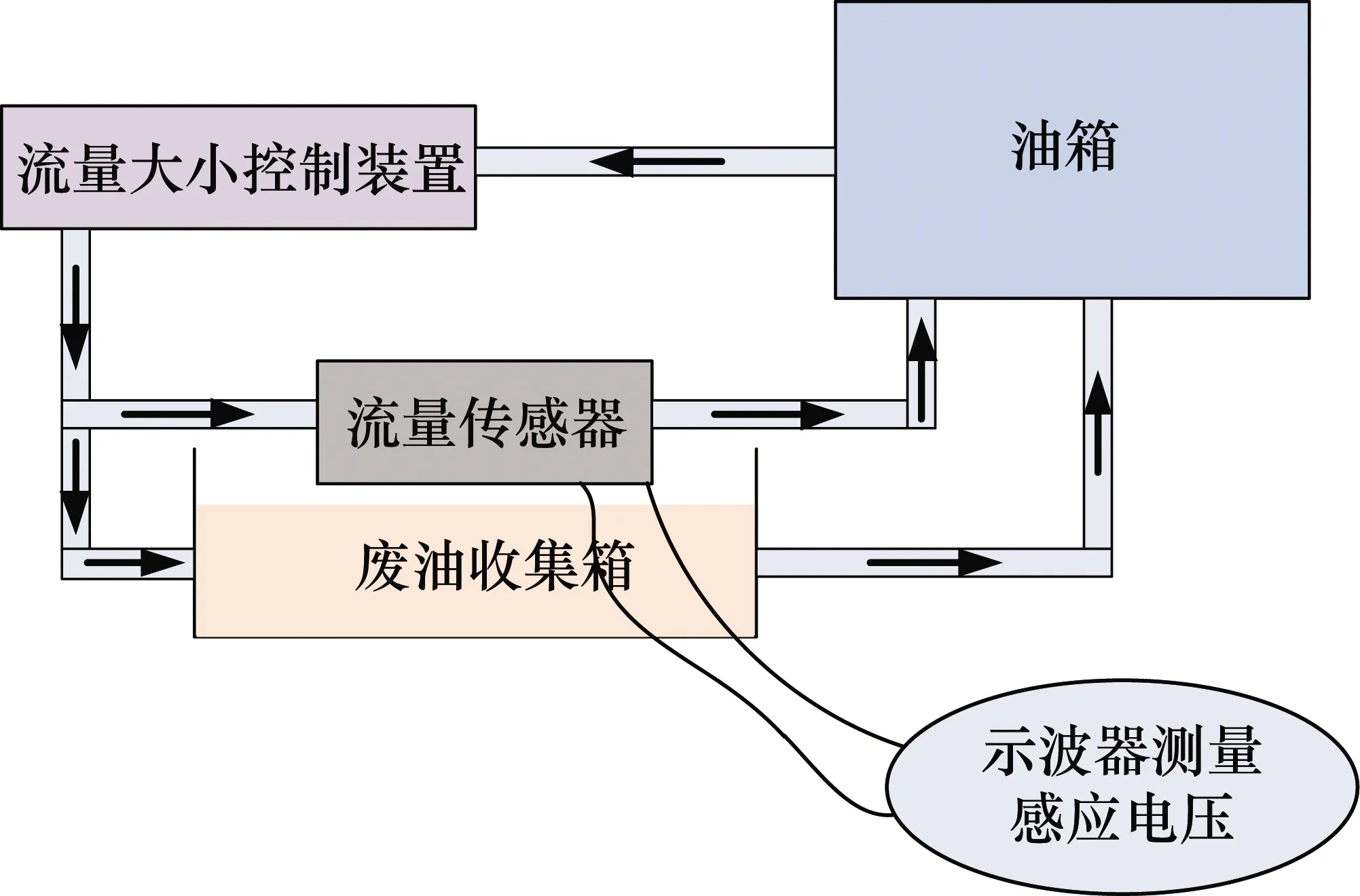
图13 实验装置示意图

表2 6组磁铁和6组线圈及10组磁铁和10组线圈产生的感应电压

对比表2的实验结果可知，6组磁铁产生的感应电压幅值远大于10组磁铁，但10组线圈产生的感应电压频率大于6组线圈。由于实验条件和仿真条件的差异，实验得到的电压幅值与仿真结果不完全相同，但其变化规律基本一致，排除人为测量误差的因素，频率特征基本满足5倍关系，说明仿真方法正确，仿真结论适用。

5 结束语

对于机载燃油流量的电磁转动测量方法，提出使用有限元技术对流量传感器设计过程中的各项参数进行仿真分析，以线圈中的感应电压幅值和频率为评判特征，逐步得到各项参数的影响效果。首先为了减小有限元模型的计算量，结合理论推导的结果，在实际产品的基础上对其中的非导磁材料进行了空气化处理，并建立了10组线圈和10组磁铁的二维对称模型，仿真结果表明磁场分布和感应电压曲线基本满足实际情况，验证了模型的正确性。然后逐次改变基础模型中的磁铁与线圈距离、铁芯相对磁导率、磁铁剩磁强度和叶轮转速，分析结果如下：磁铁与线圈之间距离的变化对线圈中感应电压幅值的影响是一种非线性关系，在同样间隔减小量的情况下，越靠近线圈，其电压变化越为明显；铁芯相对磁导率的变化对电压的影响较小；磁铁磁场强度与线圈感应电压呈线性变化趋势，磁场强度越大越有利于感应电压的检测；叶轮转速的改变会影响感应电压的幅值与单位时间内可检测的信号脉冲数，影响效果均为线性关系，且信号脉冲数与实时转速成5倍关系。最后对于其他可能存在的线圈与磁铁组合方式，仿真分析了4-4、6-6、4-6、10-6的组合所产生的感应电压曲线，由结果可知当线圈数与磁铁数相等时，组数数量的变化与产生的感应电压幅值变化呈反比关系；当线圈数与磁铁数不等时，产生的感应电压幅值较小且曲线平滑程度降低。为验证仿真结果的正确性，分别完成了6组磁铁和10组磁铁的等效实验，实验所得规律与仿真结论基本相同，即在设计传感器内部磁铁和线圈结构时，应保持其组数相同且绕圆周呈均匀分布，在综合考虑采集频率与电压幅值的情况下，可适当减少磁铁与线圈的组数。