基于有限元模拟的薄膜热流计结构设计及优化
张梅菊, 郭林琪, 黄漫国, 梁晓波, 张丛春, 刘冠华
(1.航空工业北京长城航空测控技术研究所 先进传感器技术中心,北京 101111; 2.上海交通大学 电子信息与电气工程学院 微纳电子学系,上海 200240; 3.状态监测特种传感技术航空科技重点实验室,北京 101111)
在航天航空领域,涡轮叶片作为航空发动机的核心部件,其正常工作下温度分布状态与部件的使用寿命有着直接的关系,而仅把温度作为计算和分析涡轮叶片在恶劣工作环境下的温度分布的唯一信息是完全不够的。随着科学技术的飞速发展,热流密度的测量越来越受到研究人员的关注,基于航空发动机涡轮叶片表面热流密度的测量也逐渐得到了重视和发展[1-6]。传统热流传感器存在着很大局限性,其体积较大,会影响热流测量的准确性,在对测量精度要求很高的航空航天等领域无法适用[7-8]。新型薄膜热流计以其体积小、热容量小、干扰小、不破坏部件表面气流等特点,为发动机热端部件表面热流测量提供了新的测量方法[9-12]。
热电堆式热流计测量热流范围广,输出信号大,是当前使用最广泛的测量热流密度的器件之一。本文设计了一种热电堆式薄膜热流计,并对其性能影响因素进行了分析研究:首先对热流测量理论模型进行研究,并分析了影响薄膜热流计测量结果的影响因素;然后基于理论分析设计了一种薄膜热流计,并给出了关键结构参数及材料参数;最后基于有限元的方法对不同因素对薄膜热流计的影响进行了分析,总结了相关规律,并对热流计的优化提出了意见,提出优化冷热结点温度梯度切实可行的方法和思路。分析结果表明,优化后的薄膜热流计具有更出色的热学性能与电学性能。
1 薄膜热流计设计
1.1 薄膜热流计热学模型建立
热流值Q可表示为[13]
(1)
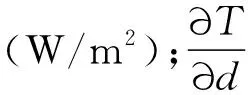
如果温度为T1和T2的两个等温面平行式[14]为
(2)
式中,T1为热结点温度(K);T2为冷结点温度(K);d为热阻层的厚度(m)。则由式(2)可知,如果热流计材料和几何尺寸确定了,那么只要测出热电堆在热阻层两侧的温差,就可以计算出热流值。根据热电堆的测温原理,热电势E的计算公式为[14]
E=SN(T1-T2)
(3)
式中,S为热电偶的塞贝克系数(μV/K);N为组成热电堆的热电偶个数。
将上述公式合并起来,得到热流密度与热电堆输出的关系为[14]
(4)
由塞贝克效应可知,薄膜热流传感器输出电势与冷热结点温度差成正比。因此,以冷热结点温度差表征薄膜热流传感器热电响应输出,研究不同因素变化对其产生的影响。
1.2 薄膜热流计结构设计
依据傅里叶定律设计薄膜热流计,主要由热电堆、热阻层组成,如图1所示。热阻层1覆盖在热电堆的热结点上方,热阻层2覆盖在热电堆的冷结点上方,由于两种热阻层材料的导热系数不同,当表面有热流Q施加时,不同的热阻层材料使得薄膜热电堆冷热结点存在温度梯度而产生输出响应,热流计输出温差电动势。热流计的结构参数及材料参数如表1、表2所示。
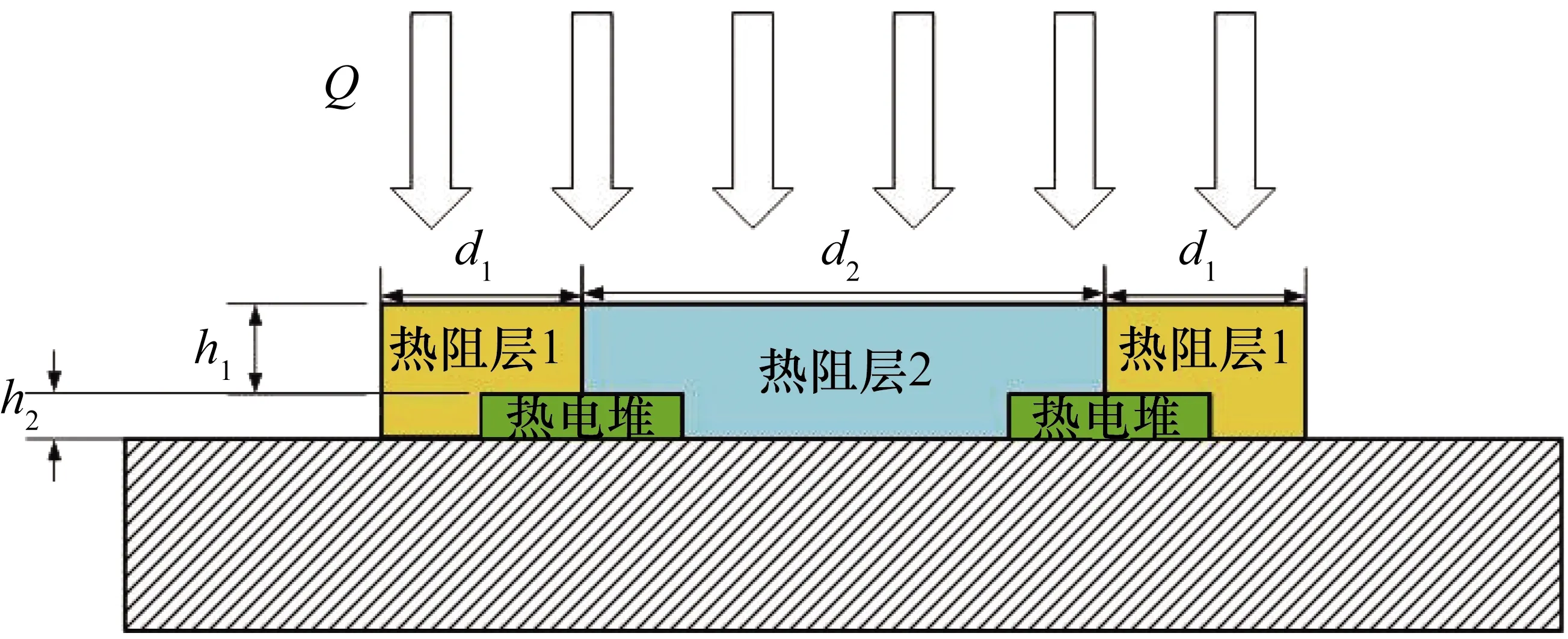
图1 薄膜热流计结构图
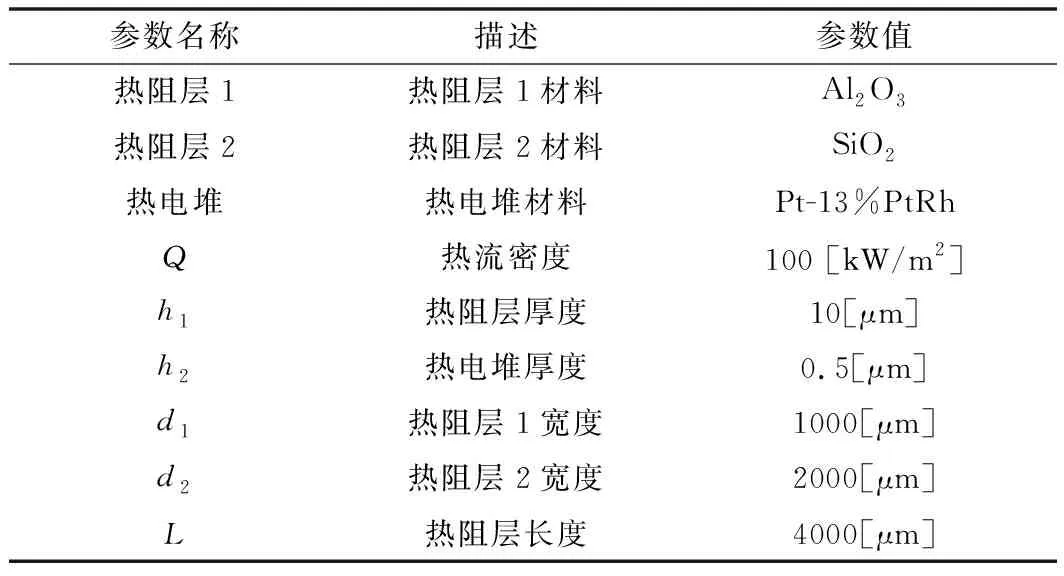
表1 薄膜热流计结构及材料参数
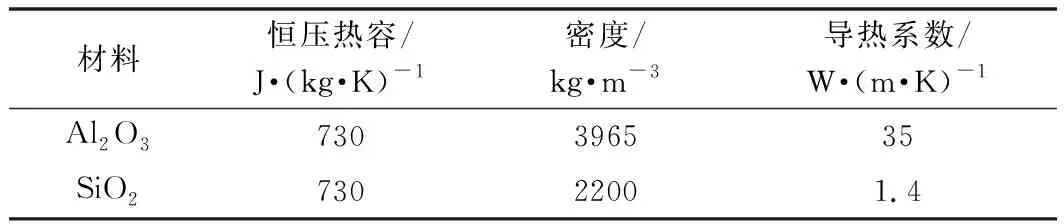
表2 薄膜热流计热阻层材料属性
2 薄膜热流计优化
2.1 薄膜热流计有限元模型建立
仿真模型如图2所示,热流计整体尺寸为4 mm×4 mm,热电堆由18对热电偶串联形成,其上覆盖了两种不同材料的热阻层。为便于求解问题,导热模型做如下假设:
① 各种材料的热物性系数为常数,不随温度变化而变化。
② 由于薄膜热流计的厚度相对于长宽可以忽略不计,只考虑表面固体传热,不考虑侧面对流换热。
③ 模型热传导分析中,由于固体间的热辐射对于固体传热和对流换热的影响非常小,可以忽略不计。故仅考虑各结构接触面间的固体传热,以及结构表面与空气对流换热,不考虑热辐射。
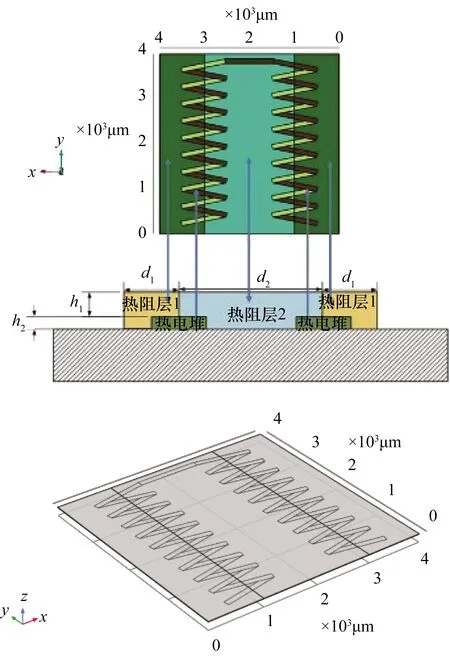
图2 薄膜热流计的设计布局
热流计与外界环境初始温度为1493.15 K,热阻层覆盖在Pt-13%PtRh热电堆表面,无空气缝隙,通过固体传递热能。热电堆厚度为0.5 μm,热阻层上表面为定热流边界条件,热流大小为Q=100 kW/m2,热阻层上表面和热电堆下表面与外界环境的换热系数为4500 W/(m2·K)[15-16]。热电堆一端接地,另一端设为悬浮电压。采用智能网格划分方式对模型进行网格划分,在结点处进行网格加密,划分网格后的模型如图3所示。
图3 薄膜热流计有限元网格划分
2.2 薄膜热流计有限元仿真
图4(a)为施加100 kW/m2的热流密度时,达到稳态后薄膜热流计内部的温度分布。热传导是主要考虑机制,由于热阻层材料导热系数的差异,当表面有热流Q施加时,热结点传热快,冷结点传热慢,故冷热结点将存在温度差,两边Al2O3热阻层导热系数大,温度高,为热结点;中间SiO2热阻层导热系数小,温度低,为冷结点。
图4(b)表示了热阻层下方热电堆上的温度分布,热结点处平均温度为1548.55 K,冷结点处平均温度1547.84 K,冷热结点温差为0.71 K。
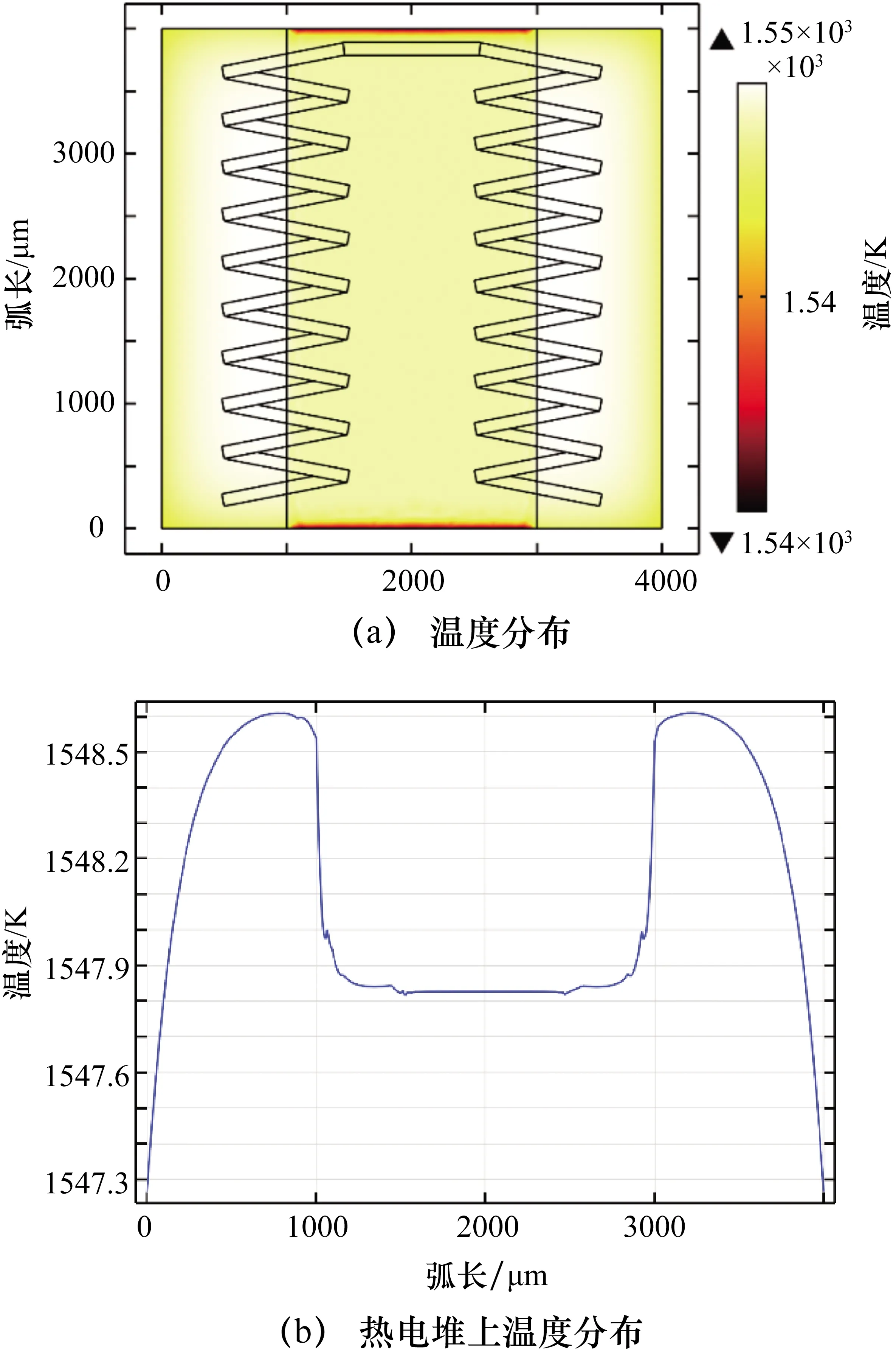
图4 施加100 kW/m2热流密度时的温度分布
基于塞贝克效应,薄膜热流计将0.71 K冷热结点温差转化为输出电压93.95 μV,在温度梯度下导体内的载流子从热端向冷端运动,并在冷端堆积,从而在材料内部形成电势差,同时在该电势差作用下产生一个反向电荷流,当热运动的电荷流与内部电场达到动态平衡时,材料两端形成稳定的温差电动势。
2.3 不同因素对热流测量的影响
2.3.1 不同热流密度对热流测量的影响
根据施加不同的表面热流密度,热流密度值分别为100,200,300,400,500,600,700,800,900,1000 kW/m2,进行仿真模拟计算。计算结果如表3所示,其曲线图如图5所示,可观察薄膜热流计冷热结点温差随热流密度的变化。
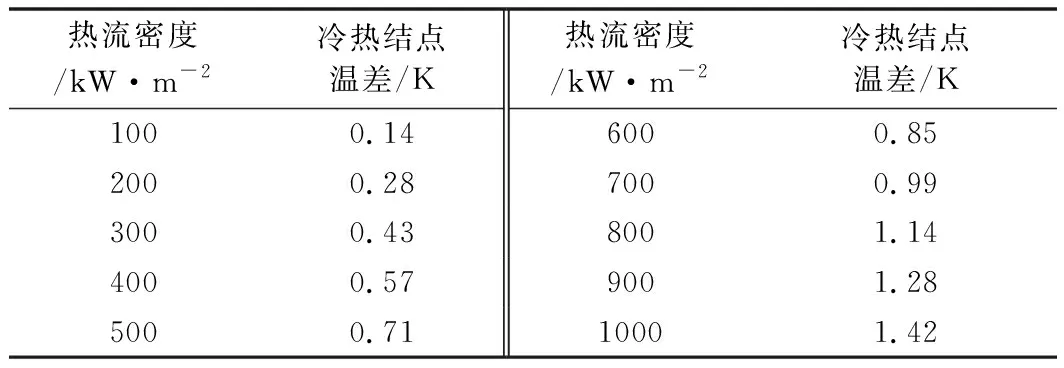
表3 施加不同的热流密度时冷热结点温差的变化
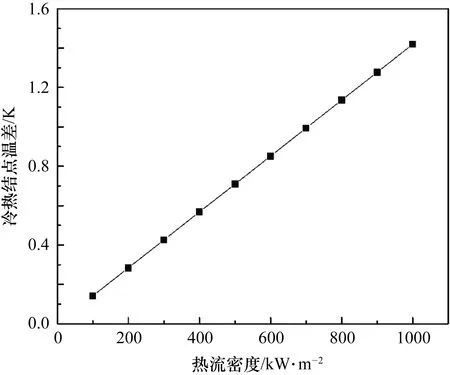
图5 施加不同的热流密度时冷热结点温差的变化
从仿真模拟结果可知,施加不同的热流密度时,稳定输出的冷热结点温差随热流密度的增大而增大。当施加100 kW/m2的热流密度时,稳定输出的温差仅为0.14 K,而施加1000 kW/m2的热流密度时,稳定输出的温差达到1.42 K。随着热流密度的增加,薄膜热流计的冷热结点温差也随之增加,且线性度良好,说明该薄膜热流传感器结构在模拟温度测试中具有良好的输出,能够作为叶片等结构件热流测量的一种传感手段。
2.3.2 不同热阻层厚度对热流测量的影响
热阻层的厚度不同,其对薄膜热流计温度的分布也有很大的影响。热阻层厚度不同,也将影响薄膜热流计与被测物,以及与外界环境的传热,从而影响被测物表面的热流分布和温度分布。通过仿真分析热阻层厚度对热流测量的影响,改变热阻层的厚度,观察热阻层的厚度不同时薄膜热流计冷热结点温差的变化曲线。
当薄膜热流计的热阻层厚度分别为1,2,3,4,5,6,7,8,9,10 μm时,热电堆层厚度为0.5 μm,施加500 kW/m2的稳态热流,观察热流计冷热结点温差的输出。不同热阻层厚度下输出的冷热结点温度和温差变化如图6所示。
从图6可得出,冷热结点温差将随热阻层厚度的增大而增大。当热阻层的厚度为1 μm时,冷热结点温差为0.08 K,然而当热阻层厚度增加为10 μm时,温差增大到0.71 K,较1 μm的热阻层厚度增大了787.5%。随着热阻层厚度的增加,薄膜热流计的冷热结点温差也随之增加,且线性度良好,说明要想提高该薄膜热流计的性能,需要增加热阻层的厚度。因此本设计的热阻层厚度相对合理。对曲线进行线性拟合,其冷热结点温差与热阻层厚度之间的关系为ΔT=0.0696h1+0.0253,其中ΔT为冷热结点的温差,h1为热阻层厚度。
2.3.3 不同热电堆厚度对热流测量的影响
当薄膜热流计的热电堆层厚度分别为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0 μm时,热阻层厚度为10 μm,施加500 kW/m2的稳态热流,观察热流计冷热结点温差的输出。不同热电堆厚度下输出的冷热结点温度及温差的变化如图7所示。
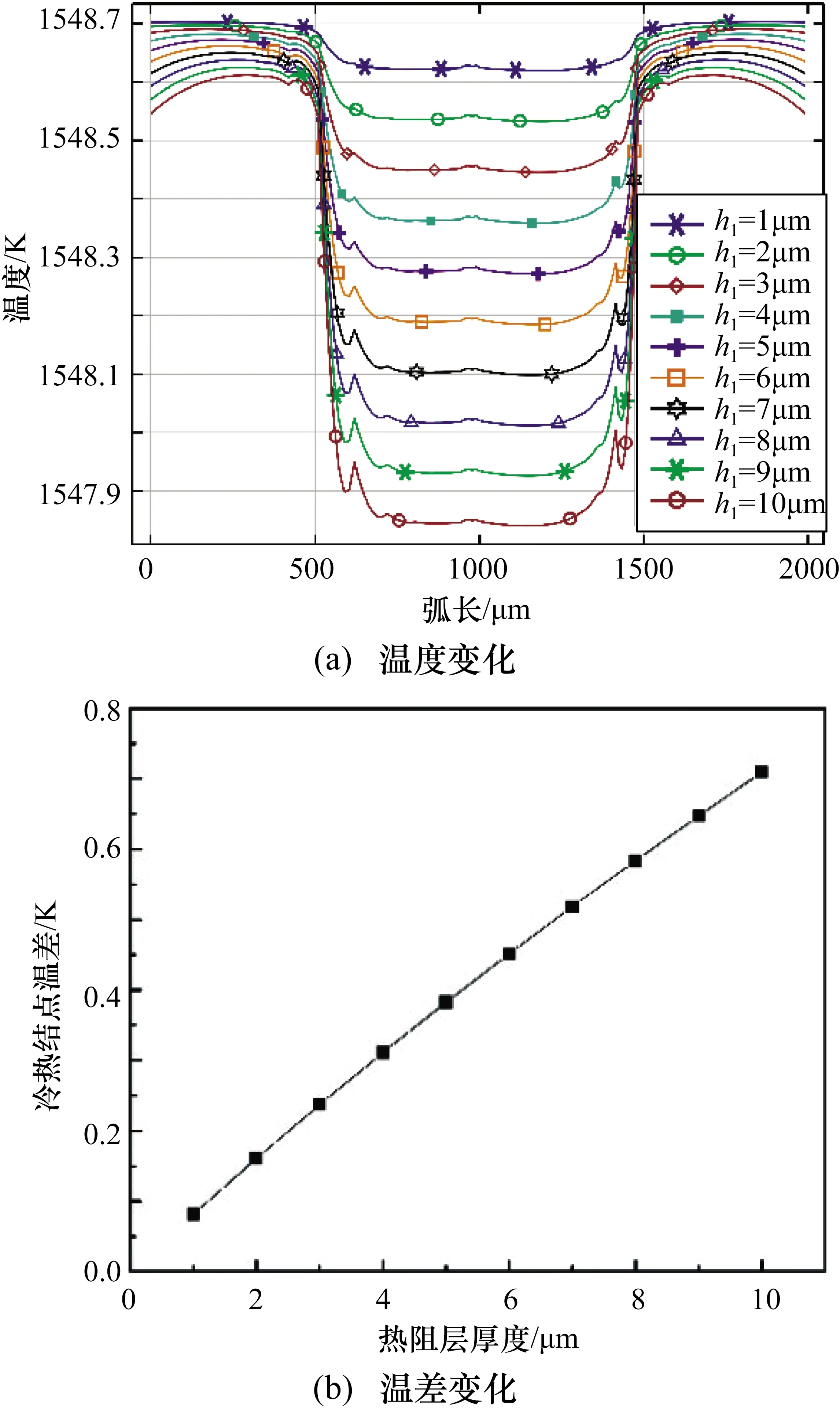
图6 热阻层厚度不同时冷热结点温度及温差的变化
从图7可得出,冷热结点温差将随热电堆厚度的增大而减小。当热电堆的厚度为1 μm时,冷热结点温差为0.67 K,然而当热电堆厚度为0.1 μm时,冷热结点温差上升到0.74 K,较1 μm的热电堆厚度增大了10.44%。随着热电堆厚度的减小,薄膜热流计的冷热结点温差也随之增加,且线性度良好,说明要提高该薄膜热流计的性能,需要适当减小热电堆层的厚度。对曲线进行线性拟合,其冷热结点温差与热阻层厚度之间的关系为ΔT=-0.0072h2+0.7459,其中ΔT为冷热结点的温差,h2为热阻层厚度。
3 结束语
本文对薄膜热流计结构进行了基于有限元方法的设计及优化,建立了有限元模型,在此基础上系统总结影响冷热结点温差的关键因素,并结合有限元分析、优选和对比,提出优化冷热结点温度梯度切实可行的方法和思路:① 增大热阻层厚度;② 减小热电堆层厚度,为结构设计合理性提供了有力的参考依据。仿真结果表明,经过优化设计的薄膜热流计具有更好的冷热结点温差输出。

图7 热电堆厚度不同时冷热结点温度及温差的变化

