浸没燃烧天然气加热装置燃烧室设计优化

戎开茹 史永征 菅海瑞 刘蓉

1.北京建筑大学环境与能源工程学院 2.中核能源科技有限公司

浸没燃烧天然气加热装置是一种新型天然气加热装置，于2017年首次投入天然气调压门站使用，换热效果满足设计要求[1]。本研究主要结合装置实际运行状况，使用理论分析及数值模拟实验研究的方法，对燃烧室设计进行优化，在保证燃烧稳定、完全的前提下，尽可能提高燃烧强度，降低NOx排放，减小燃烧室的尺寸和质量，以满足装置结构紧凑性的要求，并给出该类型燃烧室设计结构及运行工况的优化参数，为后续浸没燃烧天然气加热装置的设计提供参考依据。

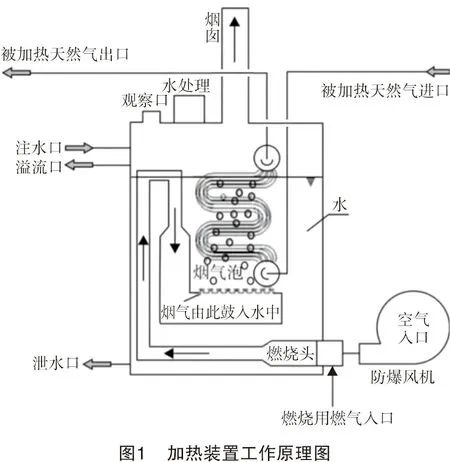
该加热装置基于浸没燃烧技术研发，主要由燃烧系统、换热系统和控制系统组成，其工作原理如图1所示。燃烧系统燃烧产生的高温烟气通过鼓泡孔进入水浴中，通过气液两相流与天然气换热盘管强化传热，以达到加热天然气的目的。

1 燃烧空间的设计

图2为装置燃烧原理图。采用风机前预混方式将空气和燃气在混合器中混合，同时搭配电磁比例阀，控制过剩空气系数的稳定性，预混气通过管道输送至圆筒形金属纤维燃烧器腔体内，经由金属纤维网孔隙流出并在其表面进行燃烧，形成均匀稳定的火焰，燃烧产生的高温烟气从烟管排出，作为加热天然气的热源。

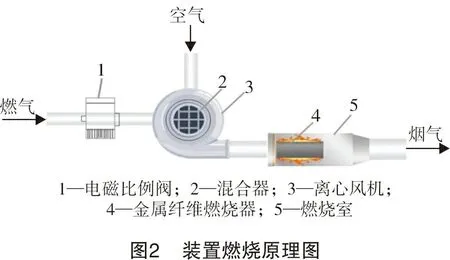
图3为在役燃烧室三维模型示意图。为了方便计算分析，本研究选取燃烧区域烟气流速最大的出口处流动截面A-A的平均速度vf代表烟气流动空间流速。

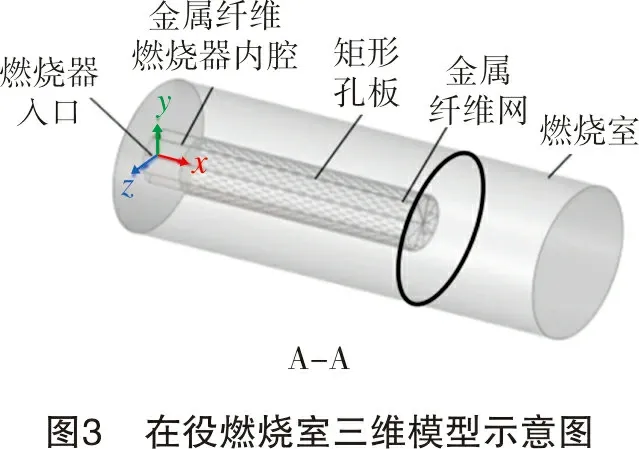
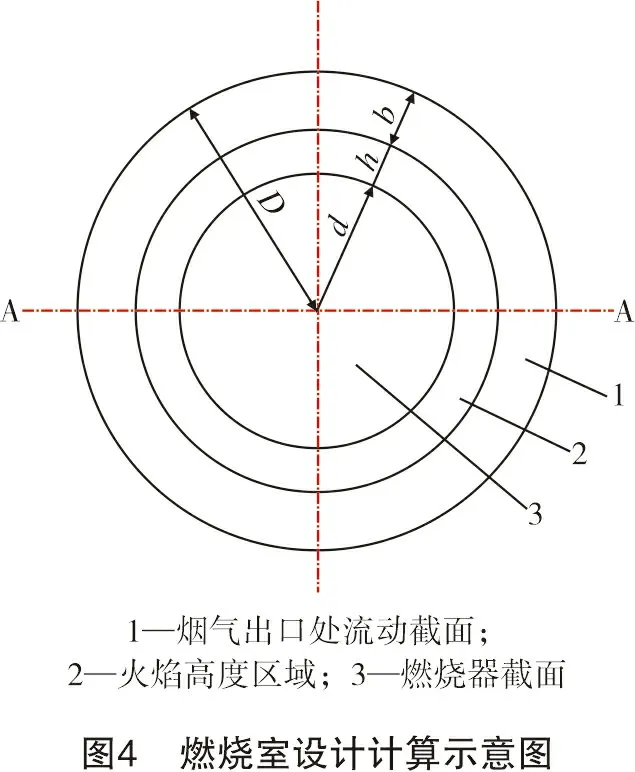
图4为燃烧室设计计算示意图。由图4可知，燃烧室出口直径D取决于金属纤维燃烧器直径d与燃烧空间的大小，而燃烧空间主要由火焰高度h及烟气流动截面宽度b两部分决定。由于烟气流速太小会增加燃烧室尺寸、太大则会出现脱火等影响燃烧的现象，所以在设计燃烧空间时，为了保证火焰的充分稳定燃烧，确定合适的烟气流动空间流速vf是关键。在确定了火焰高度h和烟气总流量qv后，通过式(1)、式(2)可以计算出烟气流动截面宽度b。

(1)

(2)

式中：vf为烟气流动空间的流速，m/s；qv为燃烧室内烟气总流量，m3/h；Fc为烟气流动截面积，m2；d为金属纤维燃烧器直径，m；h为火焰高度，m。

2 火焰高度计算

根据火焰传播机理及燃烧基础理论计算公式可得火焰高度计算关联式，见式(3)[2]：

(3)

式中：Lg、La为燃气和空气流量，由基础理论计算所得，m3/s；r为火焰内锥体底部半径，取火孔当量直径为0.001 m；Sn为平均法向火焰传播速度，m/s。

由式(3)分析可知，式中重要未知参数为层流火焰传播速度Sn，目前还没有精准的理论计算公式用于计算Sn，同时，鉴于本研究工况下用实验方法精确测定Sn的值比较困难，因此，主要使用CHEMKIN软件来辅助计算Sn值。本研究主要通过建立预混火焰传播模型进行求解：①计算预混火焰模型的基础数据，即为达到正常稳定燃烧所要求的天然气量、空气量以及预混气压力，主要根据燃烧基础理论公式进行计算；②利用Spalding理论分析方法建立一维层流火焰传播模型[3]；③利用化学动力学软件CHEMKIN计算Sn值。图5是装置在功率为200 kW、过剩空气系数分别为1.3、1.4、1.5、1.6时的SL值与火焰内锥高度的计算结果。

3 燃烧室优化模拟

3.1 物理模型及网格划分

模拟时需多次改变燃烧室直径，但整体模型无明显变化，故本研究以在役结构燃烧室直径D=219 mm作为模型示意。由图3可以看出：燃烧室筒体整体结构具有对称性，矩形多孔板中单孔尺寸小且数量多；燃烧器表面覆盖的金属纤维层是由直径为20～50 μm的金属丝烧结制成的，难以根据实际情况建模。因此，为节约数值计算成本，对计算模型进行简化，将金属纤维层视为多孔介质区域，同时，考虑到多孔板孔隙率是影响燃烧器表面气流流动形态的主要参数，可依据该参数进行简化[4-5]，最终简化为如图6所示的二维计算模型。 其主要尺寸见表1。

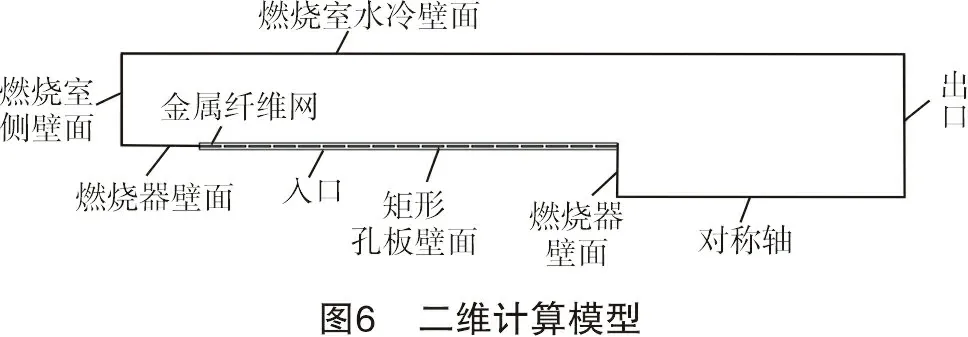
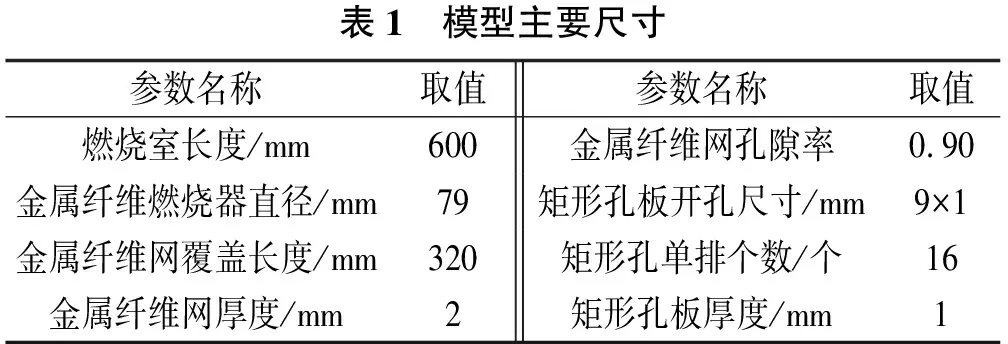
表1 模型主要尺寸参数名称取值参数名称取值燃烧室长度/mm600金属纤维网孔隙率0.90金属纤维燃烧器直径/mm79矩形孔板开孔尺寸/mm9×1金属纤维网覆盖长度/mm320矩形孔单排个数/个16金属纤维网厚度/mm2矩形孔板厚度/mm1

采用Meshing软件划分网格，网格类型为四边形结构化网格。经计算，网格数量为20×104左右，网格质量最小为0.5、网格尺寸最小为6×10-4m时，计算可实现与网格无关。

3.2 计算模型的选取

本研究中预混气整体流动为湍流状态，仅金属纤维层的流动为层流状态。故湍流模型选择ANSYS FLUENT中推荐使用的RNGk-ε模型[6-7]。预混燃烧涉及化学反应，而且燃烧器由多孔板与金属丝网组合，因此认为在实际燃烧过程中是受湍流影响的，遂考虑有限速率/涡耗散模型，该模型受化学动力学因素的影响，但其对于多步化学反应机理存在结果不正确的可能性，大多只用于单步或两步反应，无法预测化学动力学控制的因素。本研究最终选取EDC模型，将精细的化学动力学融入在湍流火焰中，参考文献[8]中五步化学反应机理的适用场景为多孔板燃烧，且最终的模拟结果较好，因此，最终选用EDC模型以及五步化学反应机理。气体辐射模型选用DO模型，NOx模型采用热力型NOx。为得到更好的收敛效果，选用压力基求解器SIMPLEC算法，离散格式均选用二阶迎风离散格式。

3.3 边界条件

入口边界条件：选速度入口，速度值为金属纤维燃烧器径向出流速度，计算见式(4)：

(4)

Fp=πdlφ

(5)

式中：vin为金属纤维燃烧器径向出流速度，m/s；qv为预混气流量，m3/s，根据燃烧基础理论计算所得[2]；Fp为火孔总面积，m2；l为金属纤维燃烧器长度，指金属纤维网覆盖区域长度，m；φ为金属纤维网孔隙率。

出口边界条件：由于燃烧应用场景为浸没燃烧，故烟气出口有一定的背压，根据装置实际运行状况可知，水浴高度为0.615 m，水位波动幅度约±0.1 m，故设置出口压力为7 007 Pa。表2为模拟工况边界条件。

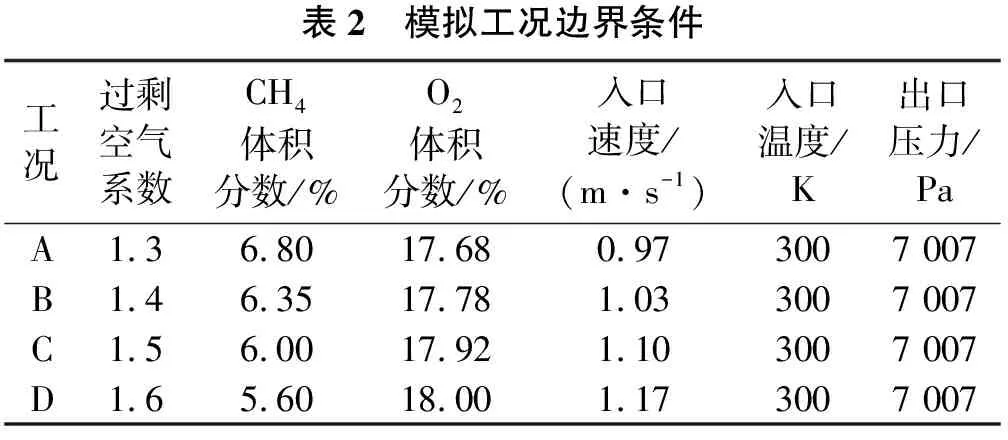
表2 模拟工况边界条件工况过剩空气系数CH4体积分数/%O2体积分数/%入口速度/(m·s-1)入口温度/K出口压力/PaA1.36.8017.680.973007 007B1.46.3517.781.033007 007C1.56.0017.921.103007 007D1.65.6018.001.173007 007

固壁边界条件：由于燃烧室浸没在水中，故将燃烧室水冷壁面设为对流传热与辐射传热的混合边界条件，环境温度设为水浴平均温度323 K，剩余壁面均设置为绝热条件。

3.4 区域条件

由于燃烧反应发生在金属纤维燃烧器表面，故假设预混气和金属纤维固体满足热平衡，选用多孔介质单温度模型，并将多孔介质金属纤维网流体域设置为层流流动。

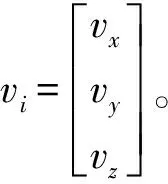
将金属纤维网简化为动量源项附加在标准流动方程模型中并进行简化，见式(6)：

(6)

低孔隙雷诺数时，惯性损失可忽略不计[9]，源项可简化为式(7)：

(7)

经冷态测试可知，金属纤维层黏性阻力系数为2.11×108s2/m。

3.5 数值仿真模型验证

为验证所选用模型的准确性，选择过剩空气系数分别为1.4、1.5、1.6时进行燃烧模拟，对比理论燃烧温度计算值与模拟计算燃烧室内烟气最高温度值、水冷壁面条件下NOx质量浓度的实测值与模拟值，结果如表3所示。由表3可见，理论燃烧温度的相对误差≤5%，NOx质量浓度相对误差≤19%，误差相对较大，这是因为模拟计算NOx质量浓度值的点位于燃烧室出口，而实测点位于烟囱的出口，该处的烟气是经过水浴换热后的烟气，有部分烟气在此换热过程中会溶于水，故NOx质量浓度模拟值高于实测值。综合分析，误差在工程可接受范围内，模型具有一定可靠性。

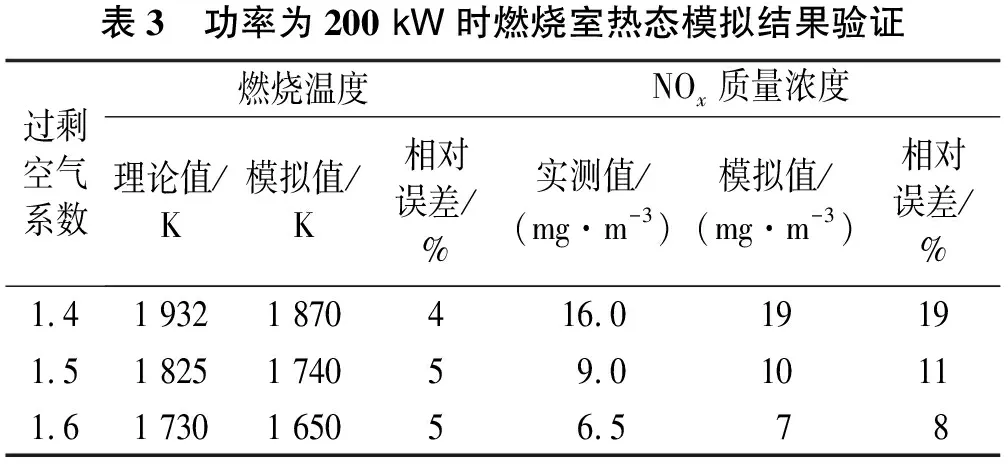
表3 功率为200 kW时燃烧室热态模拟结果验证过剩空气系数燃烧温度NOx质量浓度理论值/K模拟值/K相对误差/%实测值/(mg·m-3)模拟值/(mg·m-3)相对误差/%1.41 9321 870416.019191.51 8251 74059.010111.61 7301 65056.578

3.6 模拟结果及分析

在不同过剩空气系数下燃烧代表着不同的火焰高度工况。因此，本次模拟选定在装置额定最大设计功率为200 kW时，过剩空气系数分别为1.3、1.4、1.5、1.6的工况下，对5种不同结构的燃烧室进行水冷条件下的优化模拟。通过分析比较包含在役结构燃烧室在内的5种不同结构燃烧室，在不同过剩空气系数下的出口平均温度以及CO、NOx的质量浓度变化曲线和温度分布云图，找出最佳燃烧室结构以及最佳燃烧运行工况，并给出设计该类型燃烧室时的过剩空气系数和烟气流动空间设计流速的推荐取值范围。

表4为不同过剩空气系数模拟工况下不同结构燃烧室对应的烟气流动空间设计流速。

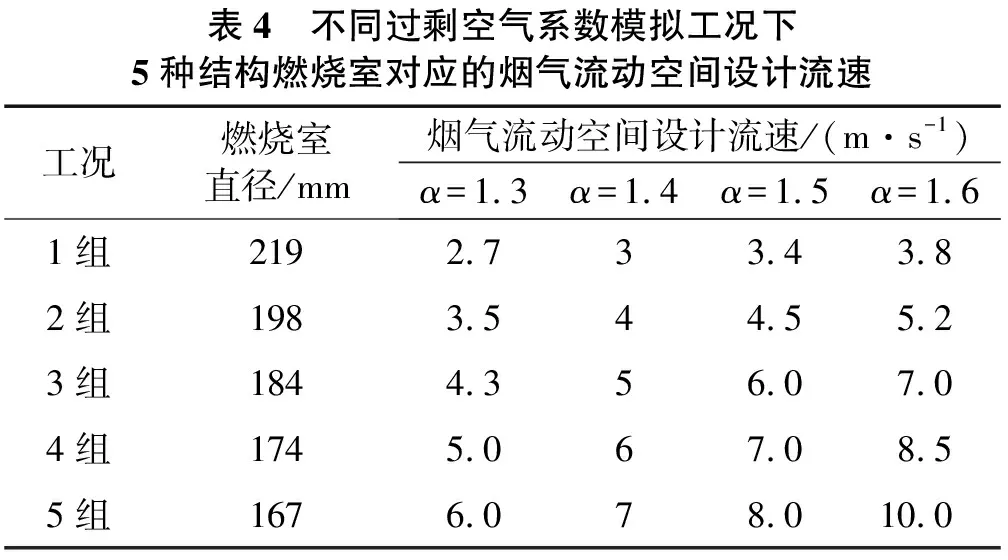
表4 不同过剩空气系数模拟工况下5种结构燃烧室对应的烟气流动空间设计流速工况燃烧室直径/mm烟气流动空间设计流速/(m·s-1)α=1.3α=1.4α=1.5α=1.61组2192.733.43.82组1983.544.55.23组1844.356.07.04组1745.067.08.55组1676.078.010.0

3.6.1最佳过剩空气系数模拟分析

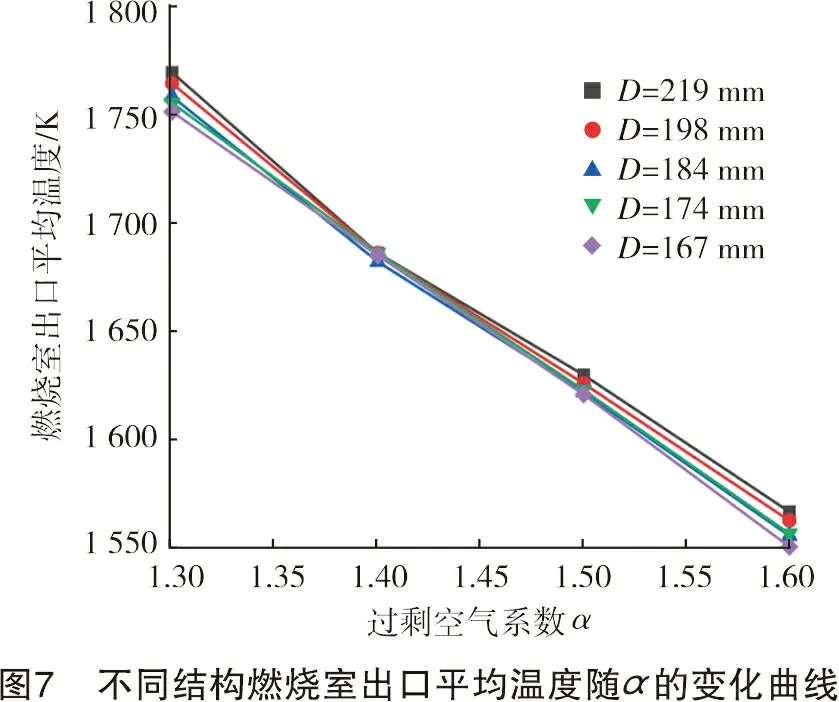
图7～图9分别为不同结构燃烧室出口平均温度、平均NOx质量浓度、出口平均CO体积分数随过剩空气系数的变化曲线。

从图7可以看出，任意过剩空气系数α下，不同结构燃烧室出口平均温度的差值在10 ℃左右，说明在一定范围内改变燃烧室结构对燃烧温度影响较小，过剩空气系数对燃烧温度的影响较大。

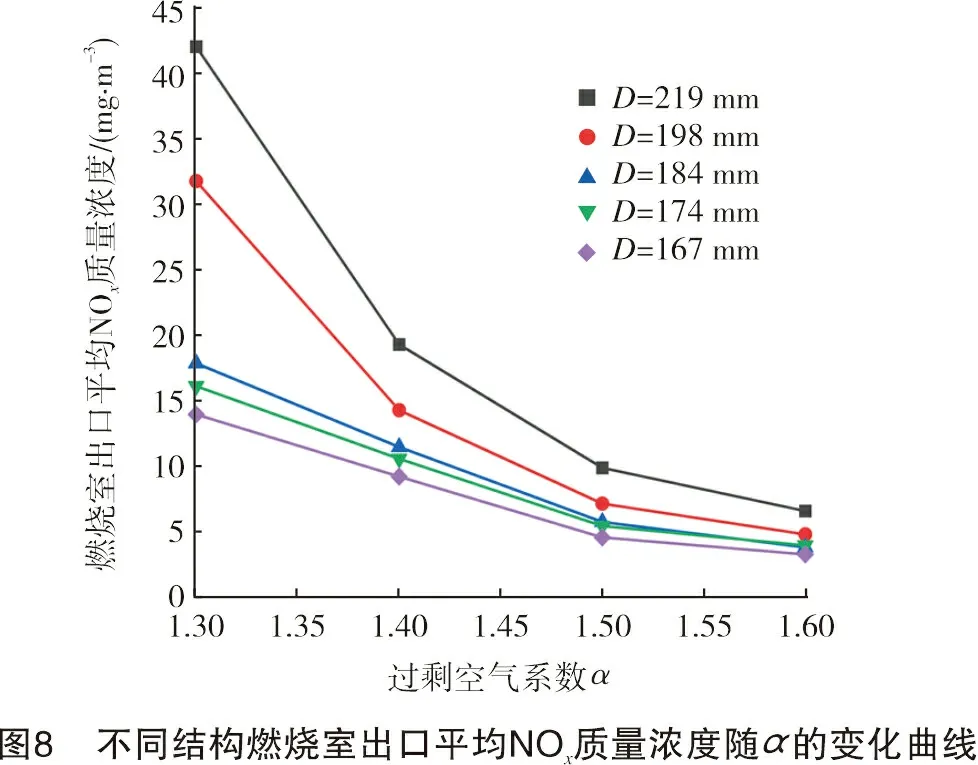
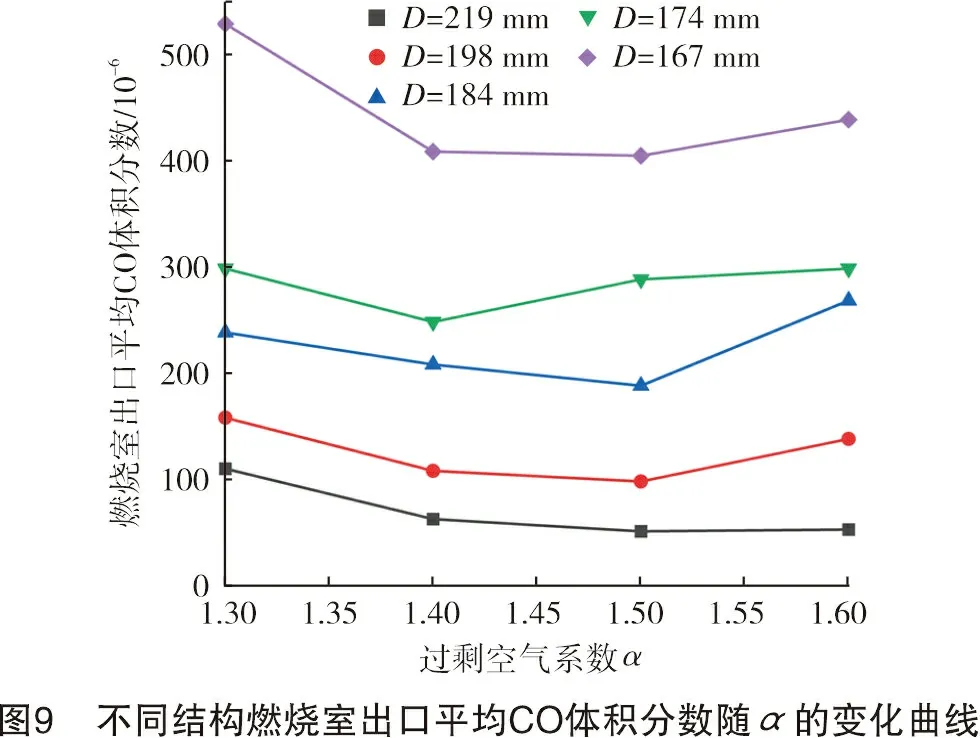
从图8、图9可以看出：不同结构下，出口平均NOx质量浓度随α增大而减小，但当α>1.5时，NOx质量浓度变化幅度减小，说明适当增加过剩空气系数，可抑制NOx生成，但抑制效果不明显；出口平均CO体积分数随α的变化曲线基本一致；当1.3<α<1.5时，出口平均CO体积分数随α增大而减小；而α>1.5时，平均CO体积分数开始增大，这是由于α>1.5时，燃烧室内的温度较低，不利于CO的转化，说明适当增加过剩空气系数有利于CO的转化。

综上分析可知：综合考虑过剩空气系数对NOx与CO排放的影响，建议过剩空气系数最佳取值为1.4。

3.6.2烟气流动空间的设计流速模拟分析

从图8、图9还可以看出：任意过剩空气系数下，出口平均NOx质量浓度随燃烧室直径的减小而降低，而出口平均CO体积分数随燃烧室减小而增大，表明在燃烧稳定不受影响的情况下，燃烧室尺寸的减小对NOx的生成起抑制作用，但不利于CO的转化。这是由于燃烧室尺寸减小导致高温烟气在燃烧室内停留时间缩短。因此，参考北京市DB11/139-2015《锅炉大气污染物排放标准》，锅炉氮氧化物的排放标准不高于30 mg/m3,CO体积分数不大于500×10-6。在保证燃烧稳定、CO的排放在允许范围内、尽量减小燃烧室的尺寸、提高燃烧室热强度，以及降低NOx排放的燃烧室结构即为最佳设计燃烧室结构，则其对应的烟气流动空间流速vf即为推荐设计流速。

图10是α=1.3时不同结构燃烧室燃烧的温度分布云图。结合图8、图9可以看出，随燃烧室直径逐步减小，燃烧稳定，出口平均NOx质量浓度递减，CO体积分数递增，但当燃烧室直径减小至167 mm时，CO体积分数超过出口限定值500×10-6。故此工况下最佳燃烧室结构对应的烟气流动空间设计流速为5.0 m/s。

图11是α=1.4时不同结构燃烧室燃烧的温度分布云图。由图11可知，改变燃烧室直径时，随着燃烧室直径的减小，烟气流动空间缩小，流动速度增大，发生脱火现象。结合图8、图9可知，D=184 mm时，燃烧较为稳定，CO排放在标准范围内，NOx排放最低。对应的烟气流动空间设计流速为5.0 m/s。

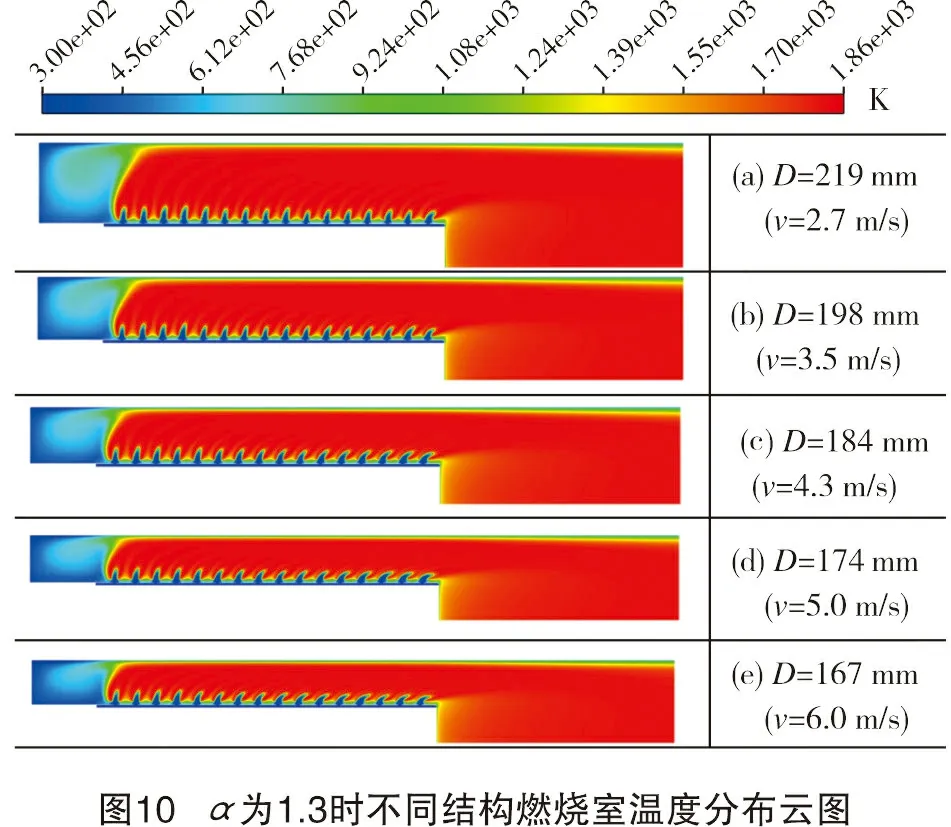
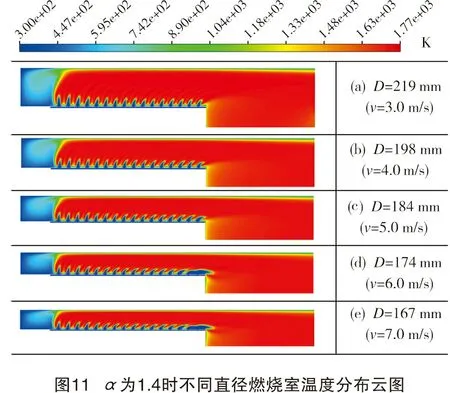
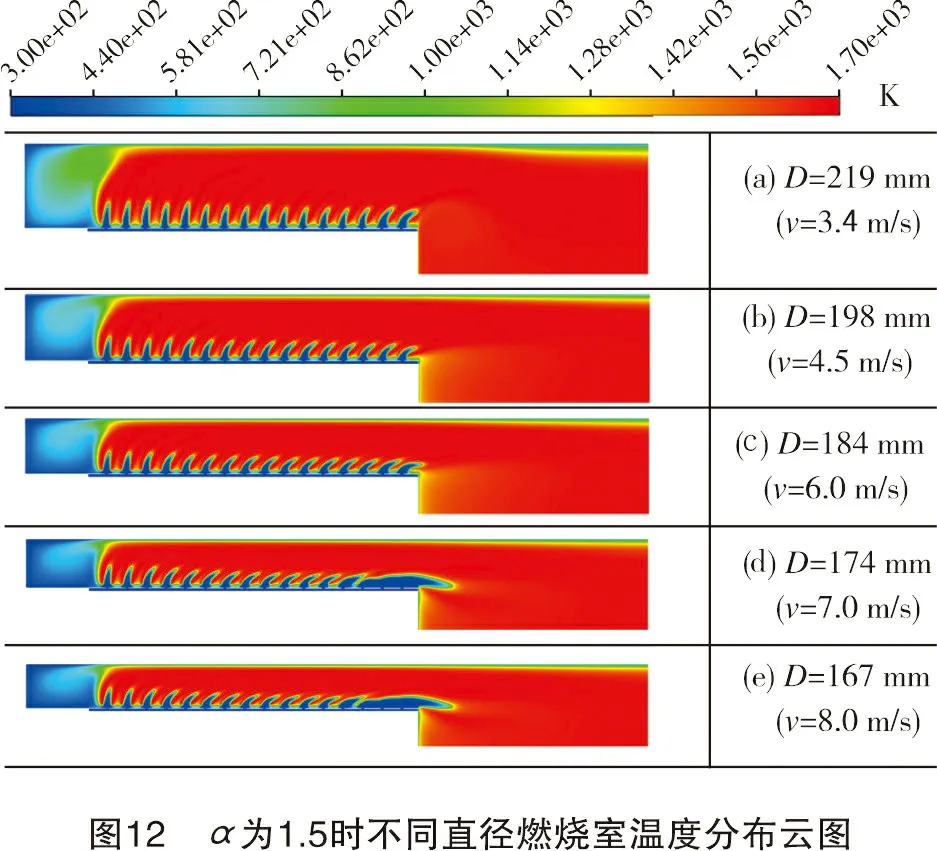
图12是α=1.5时不同结构燃烧室燃烧的温度分布云图。同上分析，结合图8、图9可知，D=184 mm时，燃烧较为稳定，CO排放在标准范围内，NOx排放最低。对应的烟气流动空间设计流速为6.0 m/s。

图13是α=1.6时不同结构燃烧室燃烧的温度分布云图。结合图8、图9可知，D=198 mm时，燃烧较为稳定，CO排放在标准范围内，NOx排放最低。对应的烟气流动空间设计流速为5.2 m/s。

综上分析可知：在不同过剩空气系数下，最佳结构燃烧室对应的烟气流动空间设计流速均约为5.0 m/s。因此，针对浸没式燃烧-圆筒形金属纤维燃烧器的燃烧室设计，建议烟气出口流动截面速度取值不高于5.0 m/s。

4 结论

结合装置实际运行情况及理论计算，使用数值模拟软件FLUENT对浸没燃烧天然气加热装置燃烧室燃烧过程进行数值模拟，得到以下结论：

(1) 综合考虑过剩空气系数对NOx、CO排放以及烟气出口温度的影响，建议过剩空气系数取1.4。

(2) 在不同过剩空气系数下，最佳燃烧室结构对应的燃烧室出口烟气流动截面速度约为5.0 m/s。因此，针对浸没式燃烧-圆筒形金属纤维燃烧器的燃烧室设计，推荐烟气流动空间设计流速取值不高于5.0 m/s。