形状对粗粒料峰值强度的缩尺影响

朱 鹏,盛 俭,李存柱,王 杰,周正华

(1.南京工业大学 交通运输工程学院,江苏 南京 210009;2.江苏长江建设工程质量检测有限公司, 江苏 南京 210009)

随着堆石坝、抛石防坡堤工程的增多以及其施工工艺的改进,堆石料等粗粒料的运用越发广泛,且最大粒径有不断增大的趋势,目前工程上使用的堆石料最大粒径已经超过了1 000 mm。传统大型三轴试验仪的试样直径一般为300 mm,高度为600～750 mm,允许的粗粒料最大粒径仅为60 mm[1],不能满足工程实际需要。为了能够进行室内试验,研究人员就需要对原粒径的粗粒料进行缩尺,研究缩尺后粗粒料的力学特性,已有的研究发现粗粒料的形状会对其力学特性产生影响。Shinohara等[2]通过三轴试验研究了颗粒形状对内摩擦角的影响;刘广等[3]研究了颗粒形状对岩石强度特性的影响;Johanson[4]将心形、圆形、星形这3种形状的塑料块涂上软蜡,粘合成试样,通过剪切试验研究颗粒形状与无侧限抗压强度的关系;严成增等[5]模拟了多边形颗粒的双轴剪切试验;刘清秉等[6]利用数字图像处理技术对砂土颗粒的形状进行量化处理,通过相对密度试验、直剪试验测试不同砂样的极限孔隙比、剪切强度指标;田继荣[7]将某筑坝堆石料筛分成3种粒组,并对其进行三轴试验,通过统计分析试验前后的形状特性,研究了形状参数随颗粒尺寸的变化规律;Wilson等[8]通过图像处理技术,通过Hough变换提出了一种量化颗粒棱角性的指标。

颗粒流数值模拟的发展为粒料力学特性的研究提供了便利。杜欣等[9]运用二值化处理和边缘点探测技术对电子计算机断层扫描(CT)获取的真实颗粒的图像进行切片处理,构建颗粒的三维模型;金磊等[10]通过CT扫描不规则颗粒,提出了一种不规则颗粒的模拟方法;仝帆等[11]通过PFC3D软件,建立不同形态的刚性颗粒簇,分析颗粒簇形态对模拟应力-应变关系以及颗粒破碎的影响;王永明等[12]采用PFC2D软件研究了不同缩尺级配试样的初始弹性模量、体积模量以及干密度极值等物理量与试样最大粒径的关系；李响等[13]通过数值模拟从细观层面揭示了室内试验尺寸效应的产生机制；文献[14-15]通过数值模拟研究了粗粒料静、动力力学特性的缩尺效应；李鹏鹏[16]通过PFC2D软件建立了4种不同形状的颗粒,研究颗粒的球度与力学特性的关系。

以上主要是针对颗粒形状的表征及形状对力学特性的影响,这些研究偏于理论化,不便于实际工程的运用。考虑到工程上关心的往往是峰值强度,研究形状系数对偏应力峰值强度的影响,不仅能使问题得到简化,而且更贴近实际的工程应用。

1 基于PFC3D软件的三轴试验模拟

1.1 接触模型的选择

在已有的研究中,通常将颗粒简化为球体以提高计算效率,采用接触黏结模型使颗粒间的黏结力代替颗粒之间的咬合力[17-18],这种简化,对于粒径较小、形状接近球体的砂、土等材料是合理的。但是对于形状各异、表面粗糙、棱角分明的粗粒料,颗粒间咬合力很大,抗剪强度也随之提高,如果延用前人的方法会使试验结果偏大,因此选择接触滑动模型。

1.2 试样的生成

本文采用的三轴试验模型尺寸为0.7 m×1.4 m,考虑到本次试验是研究颗粒形状对缩尺的影响,为了规避颗粒破碎、岩性的影响,生成了5种不同粒径和形状的刚性颗粒簇(图1)。通过时步迭代和伺服控制,使试样达到目标围压后轴向加载来模拟整个压缩过程。其中，S=d/a,d为与颗粒同体积球体的表面积;a为不同形状颗粒的实际表面积。

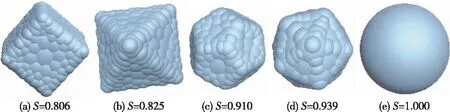
图1 5种不同球度(S)的颗粒簇Fig.1 Five kinds of clumps with different S

1.3 细观参数的选取

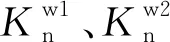
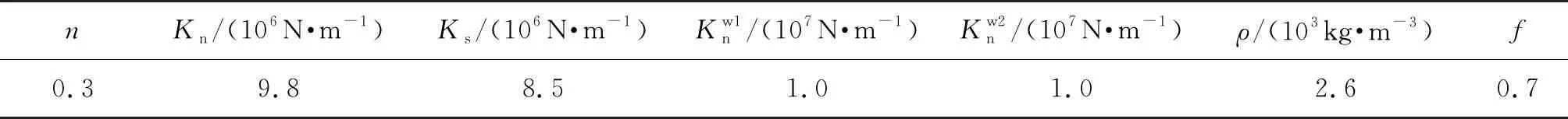
表1 模型细观参数

1.4 模拟工况

首先,保证三轴试验中每组细观参数均相同；然后,对上、下加载板分别进行加载,加载速率为

0.008 m/s；最后,以15%轴向应变作为停止加载的条件,具体的模拟工况见表2。

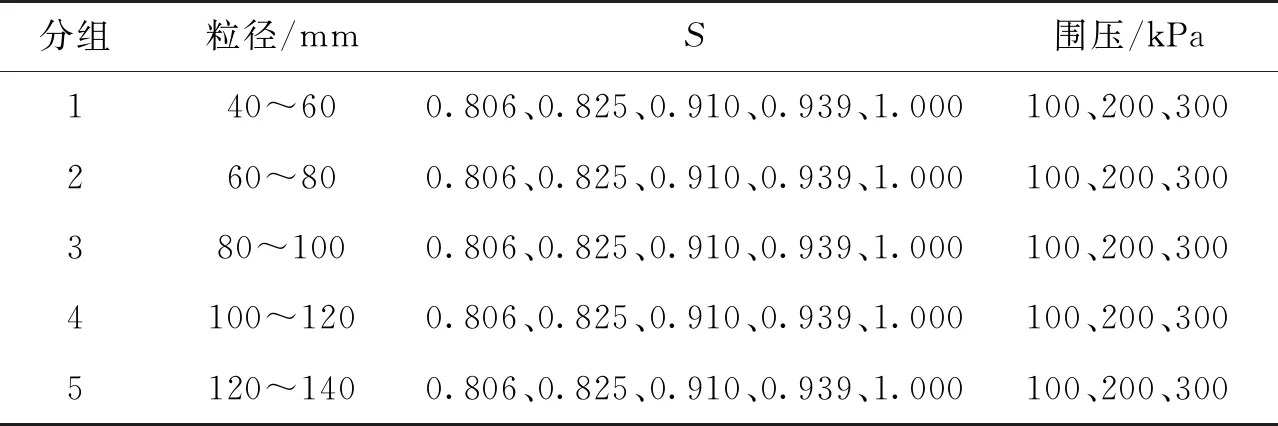
表2 三轴试验模拟工况

2 三轴试验模拟结果分析

2.1 强度特征

图2为八面体颗粒在3种围压下的应力-应变曲线。由图2可知：偏应力随着轴向应变的增大呈现先增大后减小的趋势；在同一围压下,相同形状颗粒的偏应力峰值强度随着粒径的增大而增大;当粒径相同时,偏应力峰值强度也随着围压的增大而增大。这是由于当围压一定时,试样承受的侧向约束相同,随着粒径的增大,颗粒与颗粒间的有效接触面积也会增加,产生滑动时需要的偏应力更大,因而大粒径颗粒克服摩擦阻力较小粒径颗粒发生同样的变形需要的荷载更大;当粒径相同时,颗粒与颗粒间的有效接触面积相近,当围压提高时,相当于增大了颗粒与颗粒间的约束力,当需要产生相同的位移时,围压大时就需要更大的偏应力。

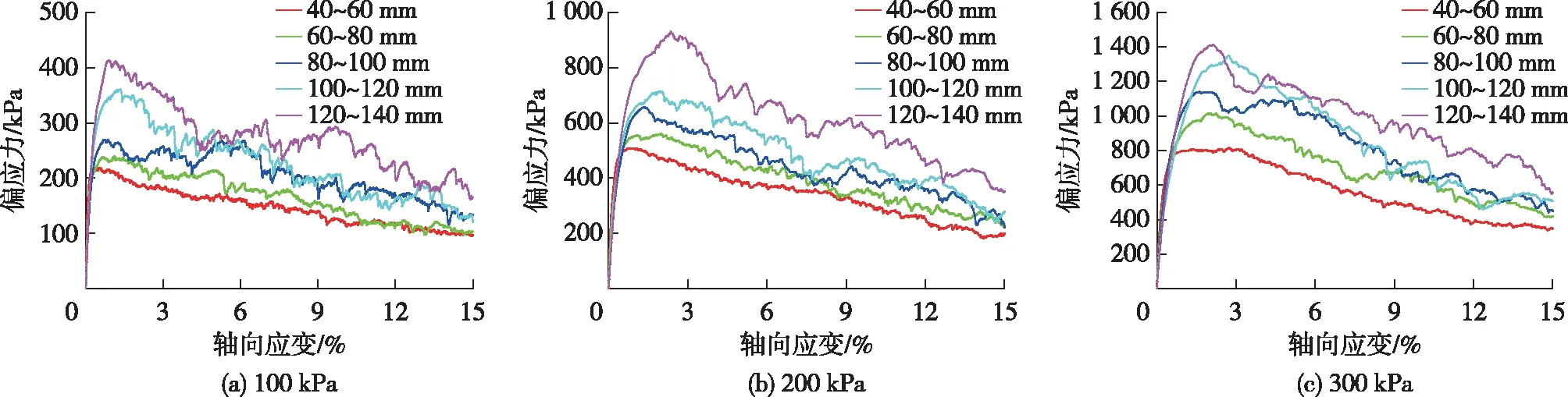
图2 不同粒径的八面体颗粒在不同围压下的应力-应变曲线Fig.2 Stress-strain curves of octahedron particles with different particle sizes under different confining pressures

图3为同一围压下不同形状颗粒的应力-应变曲线。由图3可知:不同形状的颗粒在相同粒径和围压下的偏应力峰值强度随着S的增大而减小,即颗粒偏应力峰值强度的顺序由大到小为:六面体、八面体、十二面体、二十面体、球体。这主要是因为颗粒的球度越大说明越接近球体,而球体的表面是光滑的,相较于六面体、八面体等形状,球体颗粒的表面没有突出的棱角,所以在同样的约束条件下球体颗粒与颗粒间的咬合力最小,偏应力峰值强度最低。

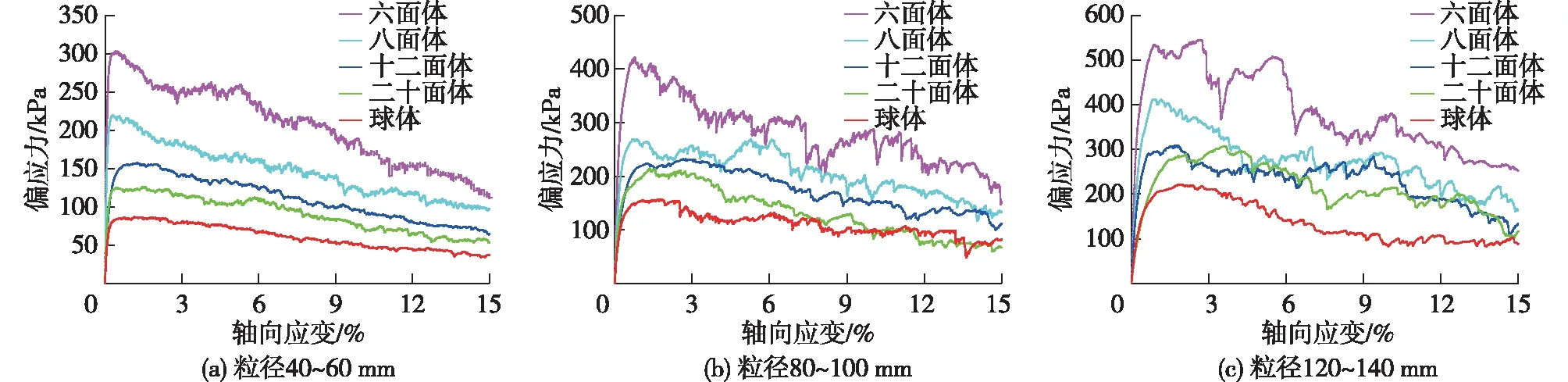
图3 不同粒径和形状的颗粒在围压为100 kPa时的应力-应变曲线Fig.3 Stress-strain curves of particles with different sizes and shapes at the confining pressure of 100 kPa

2.2 峰值强度-粒径-围压-形状间的关系

通过整理所得应力-应变曲线的偏应力峰值强度可以发现:峰值强度与围压、粒径存在线性关系,通过拟合可以得到不同形状颗粒的峰值强度(图4)。

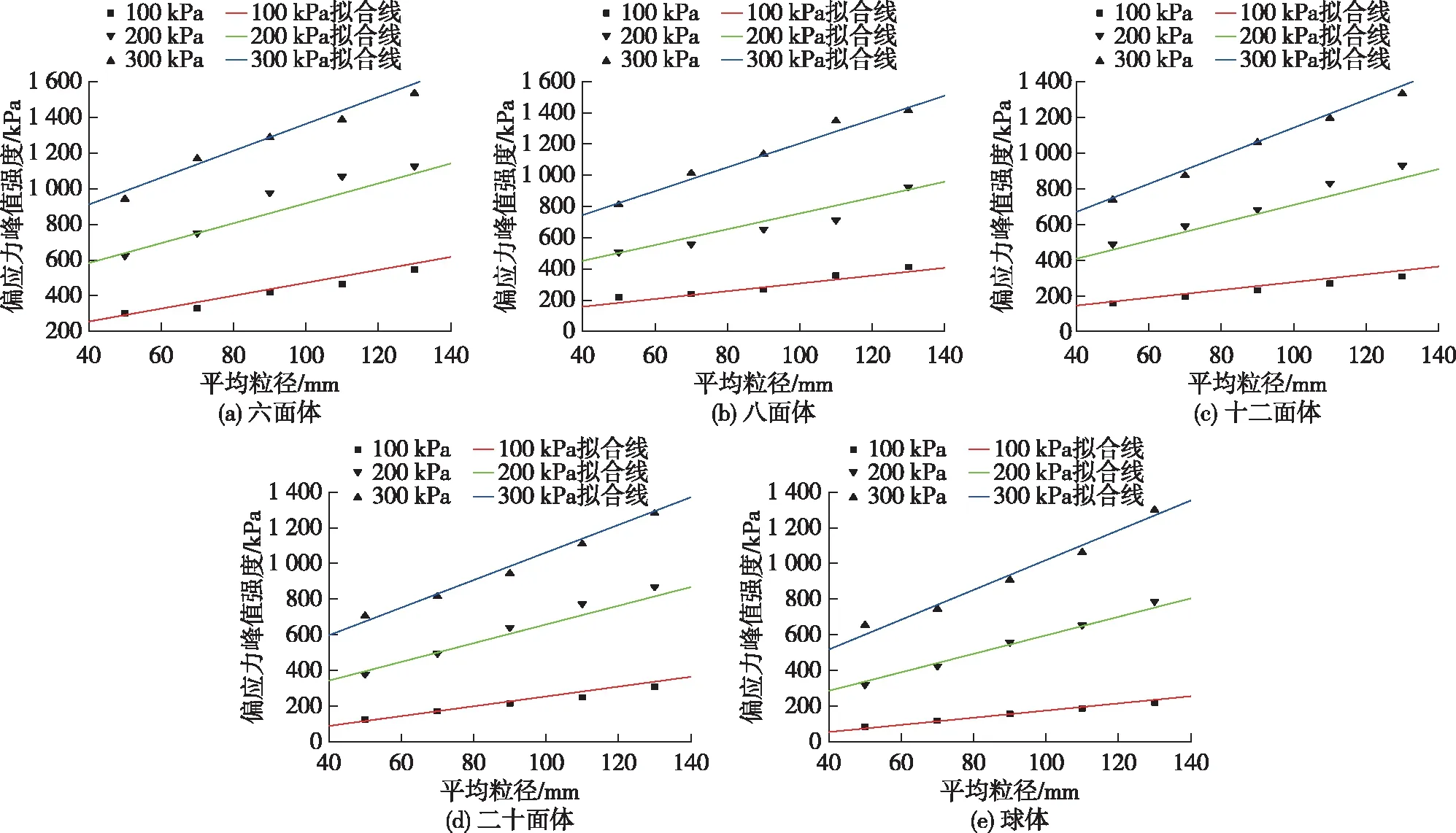
图4 不同形状颗粒偏应力峰值强度的拟合线Fig.4 Fitting lines of partial stress peak intensity of particles with different shapes

由图4可知：六面体、八面体、十二面体、二十面体、球体颗粒的偏应力峰值强度预测方程分别如式(1)—(5)所示。

σu=[249.245(σ3/pa)-138.320]+[1.958(σ3/pa)+

1.657]DS=0.806

(1)

σu=[190.564(σ3/pa)-131.427]+[2.576(σ3/pa)-

0.091]DS=0.825

(2)

σu=[148.983(σ3/pa)-91.004]+[2.839(σ3/pa)-

0.652]DS=0.910

(3)

σu=[154.328(σ3/pa)-174.970]+[2.489(σ3/pa)+0.264]DS=0.939

(4)

σu=[104.350(σ3/pa)-129.335]+[3.171(σ3/pa)-1.165]DS=1.000

(5)

式中:σu为偏应力峰值强度，kPa；σ3为模拟试验所用的围压，kPa；pa为大气压强,取100 kPa；D为颗粒的平均粒径，mm。

将式(1)—(5)整理,得到表3中不同围压下的参数a、b,并对参数进行拟合，结果如图5所示。表3中参数a为偏应力峰值强度预测方程中所对应的截距,参数b为对应的斜率。

将拟合的参数带入σu=a+bD,可得到随S、σ3、D变化的偏应力峰值强度预测方程,如式(6)所示。

σu=[-52.389-617.362(σ3/pa)]S-98.838+

727.438(σ3/pa)+[2.594(σ3/pa)+0.202]D

(6)

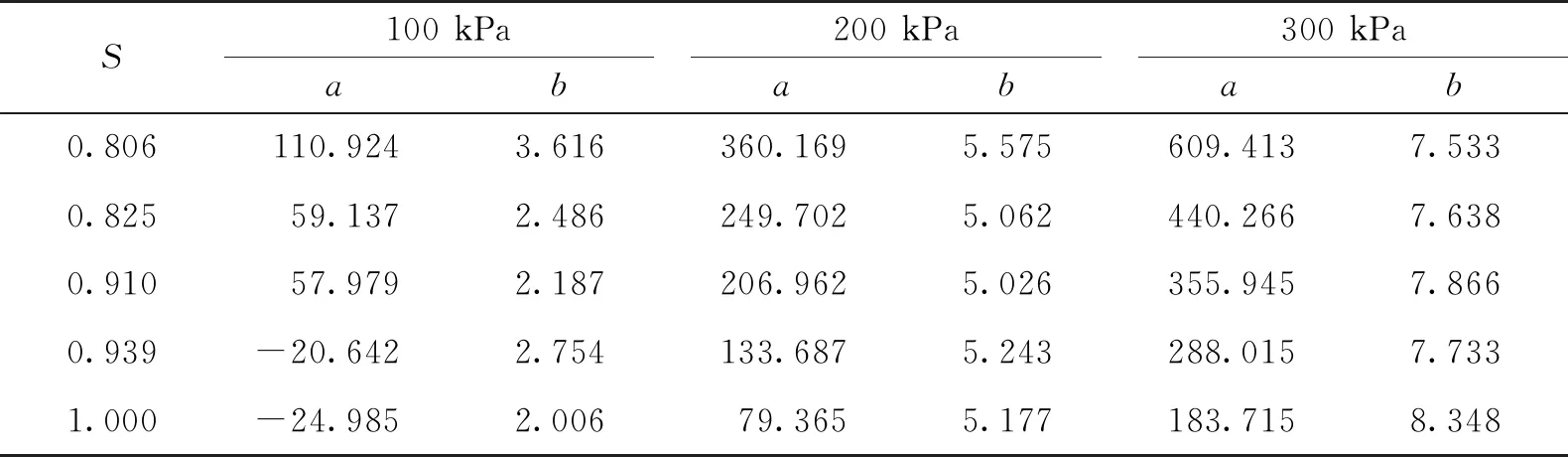
表3 5种形状的颗粒在不同围压下所对应的参数a和b

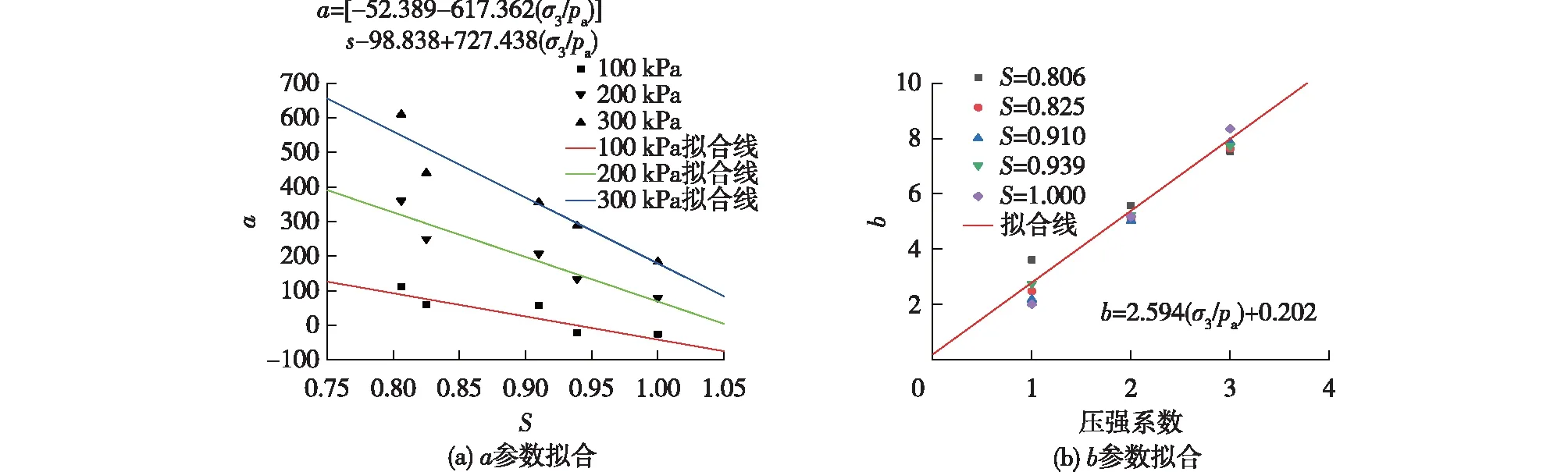
图5 不同S下对应的参数a、b拟合结果Fig.5 Fitting results of parameters a and b corresponding to different S

3 结论

本文基于颗粒流理论,通过PFC3D软件模拟不同粒径和形状的颗粒,在不同围压下进行三轴试验的数值模拟,对粗粒料宏观力学性质进行分析,并得出了偏应力峰值强度与粒径、形状、围压间的变化规律。

1)不同形状和粒径颗粒的应力-应变曲线均表现出随着轴向应变的增大,偏应力先增大后减小的趋势;颗粒在相同粒径和围压下的偏应力峰值强度随着球度S的增大而减小。

2)在相同形状和围压下,偏应力峰值强度随着粒径的增大而增大;当粒径相同时,偏应力峰值强度也随着围压的增大而增大。

3)同一形状颗粒的偏应力峰值强度与粒径间存在很好的线性关系,通过拟合得到了偏应力峰值强度随粒径、形状、围压变化的偏应力峰值强度预测方程。