不平衡电网下MMC-STATCOM的控制策略

郭殿林， 李又丰， 刘丹玉， 倪丹阳， 胡 攀

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

在煤矿供电系统6 kV母线中负荷多是交直流传动的高功率设备，该类设备作为典型的感性负载，具有大功率、低cosφ的特点，影响了煤矿供电系统的功率因数，给企业造成了一定的经济损失[1]。由此，对煤矿电力系统进行实时无功补偿是确保井下安全的重要保障。无功补偿装置的补偿性能不仅取决于采用的拓扑结构，其电流内环和电压外环控制策略也决定其性能的好坏，因此,对其优化设计具有重要意义。

随着电力电子技术的发展，提出了MMC拓扑[2]，其具有模块化扩展和高效的特性，可以通过增加功率模块的数量实现主电路容量的扩展，通过合成阶梯波输出电压，其输出频谱更好，省去了多个变压器，实现使用低压电平设备传输大功率成为可能。基于MMC的STATCOM可以针对不平衡电网实现无功及负序电流的补偿，有效地改善电能质量。Zhu等[2]研究了一种基于MMC-STATCOM的新型电路拓扑，提出了采用三角函数的动态检测无功方法，其克服了跟踪无功电流时直流环节电容器电压受负载干扰影响的缺点。刘亚昕等[3]在环流抑制中采用改进重复控制，其原理是离散化内模原理结合重复控制的抑制谐波特点。戴珂等[4]提出了一种无公共直流储能环节的改进型 MMC-STATCOM拓扑，对其使用基于等效模型的上层和基于子模块的下层控制组成的分层式控制架构。胡祺勇等[5]采用反馈线性解耦控制，设计了解耦后的系统滑模控制率。孙伟莎等[6]针对不平衡电网电压下MMC的运行，提出了基于直接功率控制的滑模变结构控制策略，其对比PI控制具有更好的快速性和稳定性。Ke等[7]在MMC-UPFC应用中提出了无源控制器与滑模变结构控制相结合，提升了快速响应和鲁棒性。王鹏飞等[8]在星形链式STATCOM的系统结构中，采用PI+反馈型重复控制的电流控制策略，使其具有良好的阶跃响应和谐波补偿性能。

上述文献对于不平衡电网下电网电流不平衡控制提供了一定的理论和实践基础，但考虑到不平衡电网下的复杂性与动态补偿，为此，笔者在不平衡电网下使用MMC-STATCOM，首先，建立基于MMC-STATCOM的数学模型，然后，利用改进SOGI提取电流、电压正负序，其次，通过电压外环采用滑膜控制和电流内环采用PI+重复控制的控制策略实现整体控制，最后，在Simulink软件中构建了11电平的MMC-STATCOM模型，验证所提出的控制策略的有效性。

1 系统拓扑与数学模型

1.1 MMC-STATCOM拓扑结构

MMC-STATCOM本质是将MMC换流器视为电压源，MMC的交流输出接到电网上，按需求为负载提供无功补偿电流，其系统结构如图1所示。

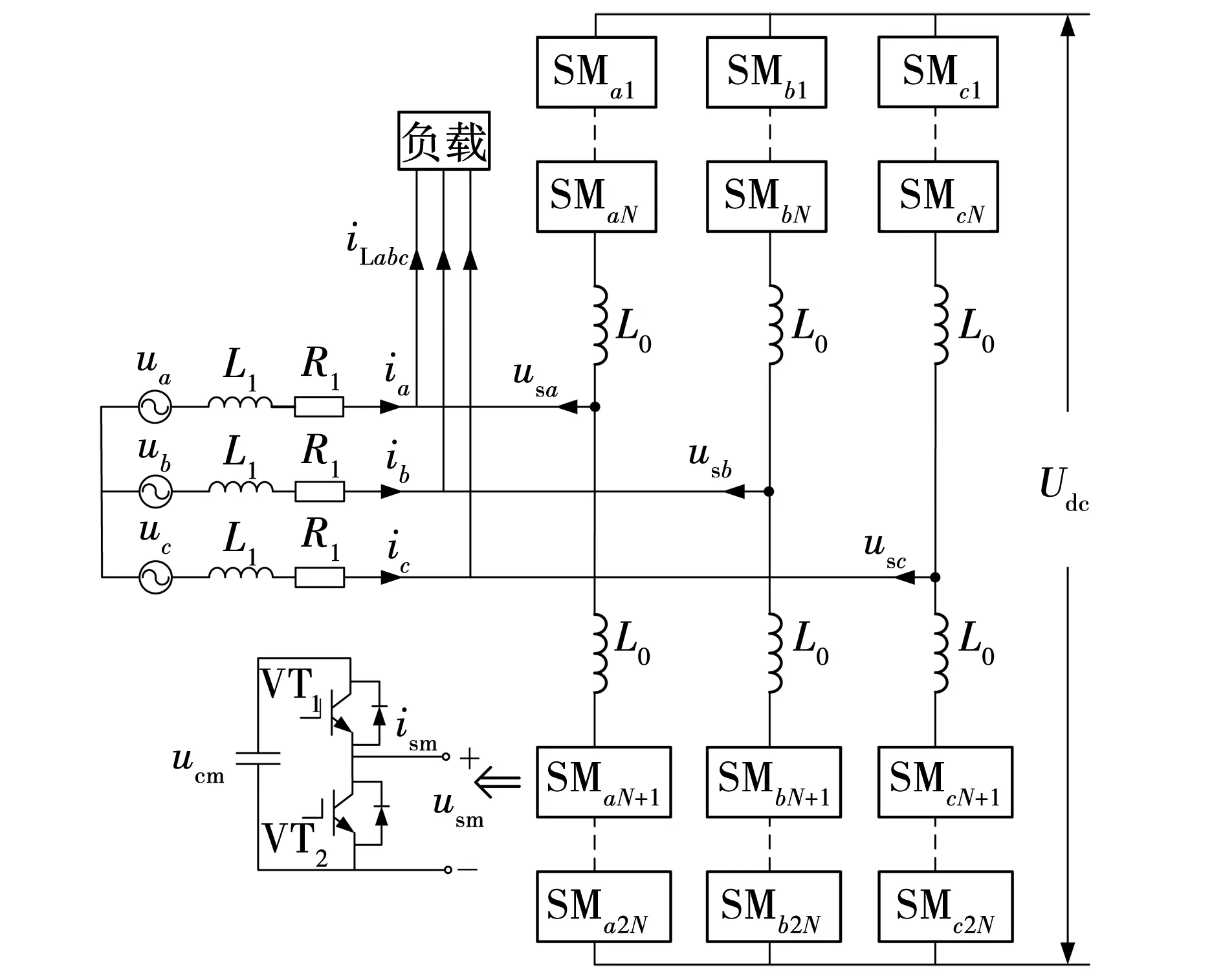
图1 MMC电路拓扑Fig. 1 Circuit topology of MMC

1.2 系统数学模型的建立

由图1可见，由基尔霍夫(Kirchhoff)定律，可以得到系统的数学模型为

(1)

Rsh=R1+R0/2，

Lsh=L1+L0/2，

式中：ua、ub、uc——电网三相abc输出电压；

usa、usb、usc——换流器侧三相abc电压；

ia、ib、ic——换流器输出电流；

Rsh——等效电阻；

Lsh——等效电感。

将式(1)进行d、q变换，得到d、q旋转坐标系中的数学模型为

(2)

式中:ud、uq——电网电压的d、q轴分量；

id、iq——输出电流的d、q轴分量；

usd、usq——换流器输出交流电压的d、q轴分量；

ω——角频率。

1.3 改进双SOGI的正负序提取

传统SOGI的传递函数为

式中：vα(s)、vβ(s)——滤波处理的α、β轴输出；

vi(s)——输入信号；

s——拉式变换算子；

ω0——无阻尼自然频率；

k——阻尼系数。

由于传统的SOGI中的D(s)具有零点，能够消除直流分量，而β是低通滤波器，直流电压波动会使输出出现一定程度上的偏差，从而影响正负序的提取。文献[9]提出改进算法，改进后的传递函数为

(3)

由式(3)得出，算法框如图2所示。改进后SOGI其实为高通后面串联了带通滤波器，如此多次谐波及直流分量更加便于去除和控制。

图2 改进后SOGI算法Fig. 2 Modified SOGI algorithm

改进后双SOGI正负序提取原理，如图3所示。

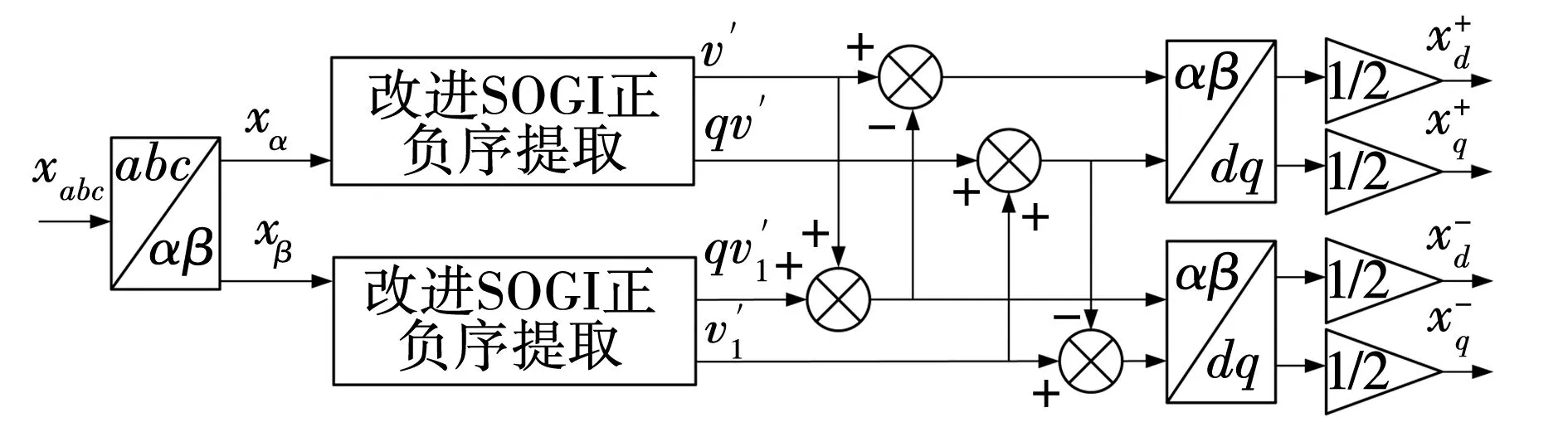
图3 改进双SOGI正负序的提取Fig. 3 Positive and negative sequence extraction graph of modified double SOGI

2 PI+重复控制策略

以内模原理为理论基础的重复控制，能够对控制系统中的某一个指令进行无静差的跟踪，可以将其视为正反馈与延迟环节的组合，正反馈环节起到累加信号，进行积分，延迟环节使信号延迟1个周期输出。仅PI控制对非线性因素的影响无法有效改善，要保证系统补偿基波稳态无差、补偿谐波能力均有提升，需要利用重复控制进行完善。由于在d、q轴下控制结构一致，因此，仅给出d轴下的重复控制原理如图4所示。

图4 重复控制原理Fig. 4 Repetitive control program structure

通过获得前一个周期的误差，实现系统误差小的目的，同样，能输出准确控制量，利用两个指标Z-N+k和S(z)在下周期对控制对象进行控制量作用，实现误差减小，达到控制目标。

由图4可知，误差信号与输入信号的传递函数为

(4)

式中：G(z)——被控制对象；

Q(z)——阻尼系数；

S(z)——补偿网络；

N——基于完整工作周期的采样点数；

k——超前拍数。

根据小增益原理有以下不等式

|Q(ejωT)-S(ejωT)G(ejωT)|<1,ω∈[0,π/T]。

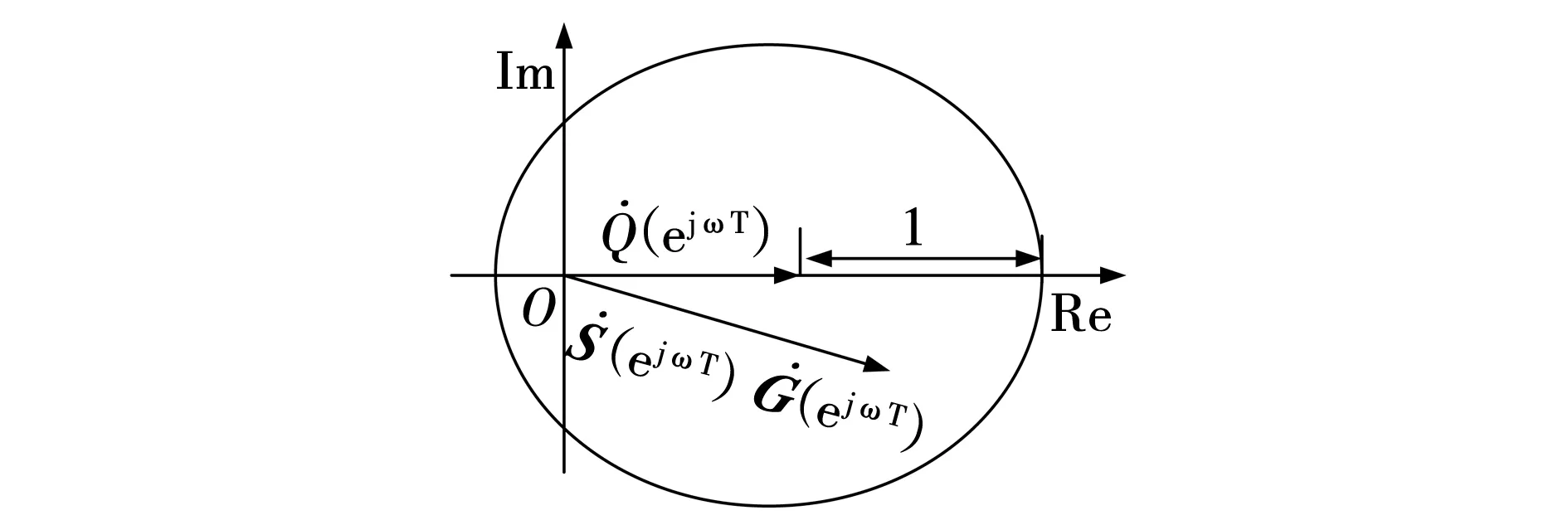
图5 稳定性条件的几何解释Fig. 5 Geometric interpretation of stability conditions

由于响应速度相对较慢，重复控制在具体应用时存在滞后性问题，综合运用PI与重复控制器相结合的控制原理，实现稳态无差跟踪控制目标，构建PI+重复控制原理如图6所示。

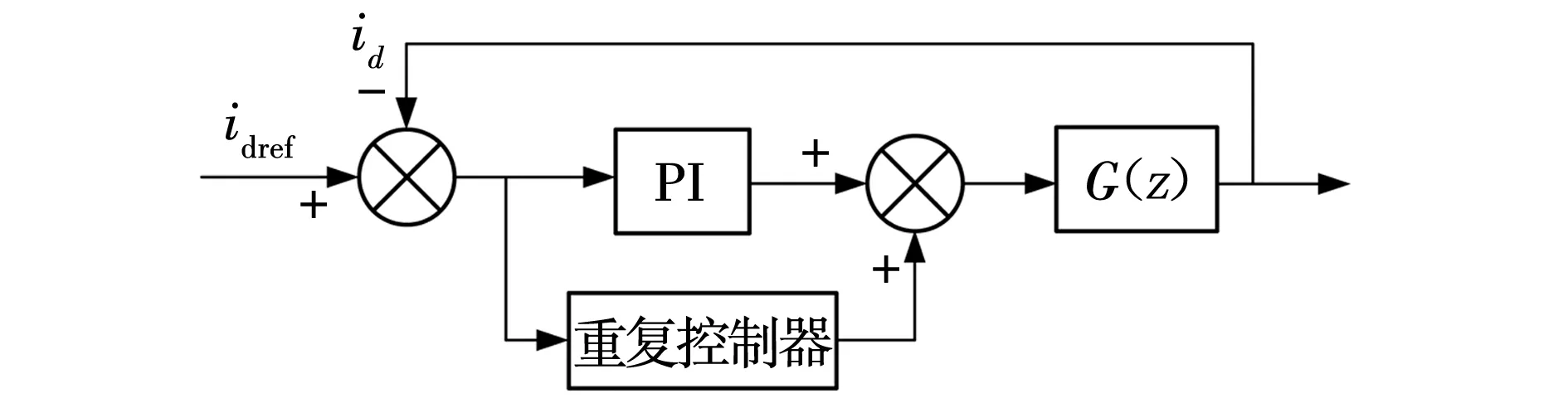
图6 PI+重复控制原理Fig. 6 PI+ repetitive control structure

3 MMC-STATCOM的控制系统结构

根据式(2)的数学模型，经式(3)正负序提取后模型为

(5)

(6)

根据上述原理和式(4)～(6)，如图7所示。

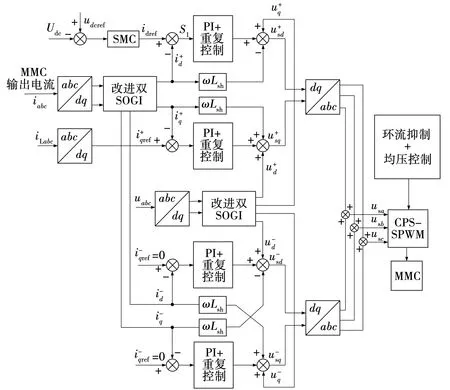
图7 控制策略结构Fig. 7 Block of strategy control

不对称电网时，控制目标是抑制负序电流，避免功率器件电流超限，因此，负序内环电流的输入控制中，负序电流参考值直接取零，以消除负序电流。经解耦控制得到的负序和正序电压信号相加加入环流和均压控制环节后进行载波移相调制，得到MMC的控制信号。

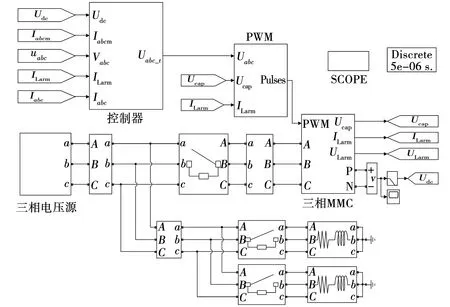
4 仿真分析与验证

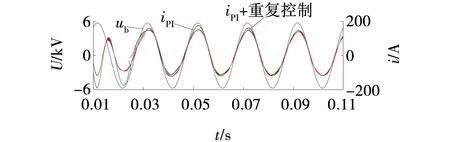
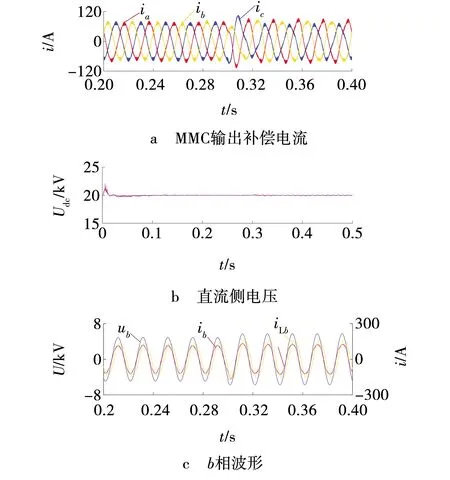
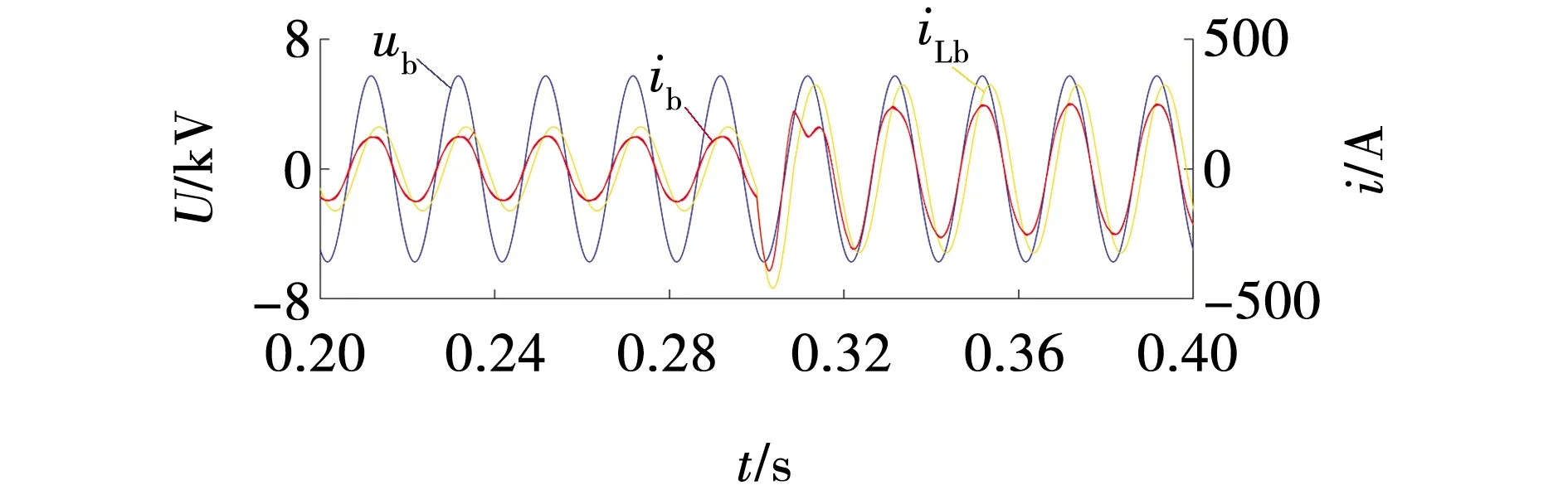
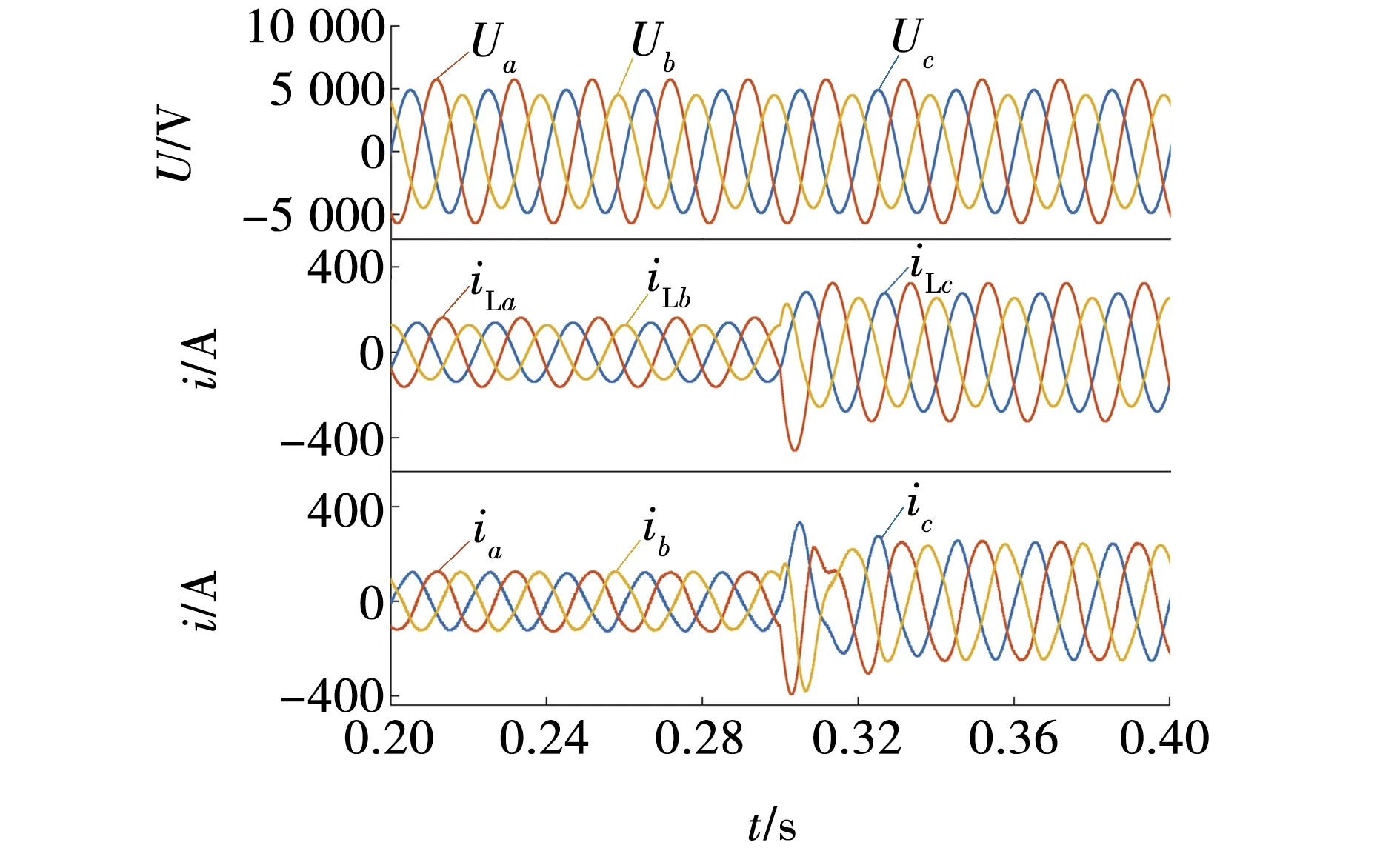
为验证所述控制的有效性，在Matlab / Simulink中构建了11电平仿真系统，如图8所示。由于文中研究的无功补偿应用于煤矿电网。因此，选用6 kV电压母线，系统的具体参数见表1。在重复控制中参数N代表采样的次数，当采样的频率和电网的频率分别是10 kHz和50 Hz时，则对应的N算出为200。参数Q(z)代表重复控制器积分系数，其取值范围为[0,1]且为常数。仿真中取Q(z)=0.95。ksz-N+k为补偿环节，需要对误差积分的ks倍进行累加，即上一周期的误差数据将成为下一周期的数据基础，若k=1，则ks此时就是重复控制器的增益系数。综上，当Q(z)取0.95时，可有-0.05

表1 系统仿真参数

当系统工作在不平衡电网下时，对比PI控制和文中所用控制，为使对比结果清晰明了，取b相电压并使电流放大得到的仿真结果如图9所示。结果表明，文中所使用的方法相较于传统的纯PI控制有较好的快速性和鲁棒性。系统工作平衡电网下，0.3 s突变为不平衡电网工况， 仿真波形如图10所示，图10a为MMC输出补偿电流，图10b为直流侧电压波形，图10c为取b相单独观察，相位、幅值得到了很好的补偿，图11为三相的仿真波形，能够看到各相电流幅值都被补齐了，功率因数达到0.99以上。

系统工作不平衡电网下，0.3 s时阻性负载突变，仿真输出结果波形为图12、13所示。由图12和13可以看出，相位和幅值得到了很好的补偿。因此，得出文中所用控制策略动态稳定性较强。

图8 系统仿真Fig. 8 System simulation

图9 不平衡电网下b相仿真波形Fig. 9 b-phase simulation waveform under unbalanced power grid

图10 平衡电网突变为不平衡电网仿真波形Fig. 10 Simulation waveform of sudden change from balanced power grid to unbalanced power grid

图11 平衡电网转不平衡电网三相仿真波形Fig. 11 Three-phase simulation waveform of balanced power grid to unbalanced power grid

图12 不平衡电网下负载突变b相仿真波形Fig. 12 b-phase Simulation waveforms of load sudden changes in unbalanced power grid

图13 不平衡电网下负载突变三相仿真波形Fig. 13 Three-phase simulation waveform of load sudden change in unbalanced power grid

5 结 论

(1)针对传统双SOGI对正负序进行提取中出现输出问题，使用改进双SOGI控制策略能够有效改善直流电压波动出现的偏差现象。

(2)在不平衡电网中，针对传统的PI控制策略的速度问题，双环解耦控制中采用滑模电压外环与PI+重复控制电流内环相结合的双环解耦控制策略，明显提高了系统的控制速度和整体动态稳定性，功率因数在各工况下均能达到0.99以上。