走线架系统实时混合实验系统及其性能

许国山， 郑力畅， 孙国良， 王 贞， 张学中， 王 涛

(1.哈尔滨工业大学 土木工程学院， 哈尔滨 150001； 2.信通院(保定)科技创新研究院有限公司， 河北 保定 071000； 3.武汉理工大学 土木工程与建筑学院， 武汉 430070； 4.黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

根据生命线工程的要求[1]，为保证地震时灾区信息传输的安全性和稳定性，常用的通信设备需要有抵御地震作用的能力。传统的走线架测试方法主要是利用有限元软件进行模拟分析[2]，或者是仅研究其悬挂系统的力学性能[3]，不能很好地反映试件本身在地震作用下的响应。另外缺乏对走线架系统与管线系统的整体分析，而无法准确地掌握整体走线架系统在地震下的响应。故需要开展许多走线架系统相关的实验。

对结构及构件的主流实验方法分为3种，即拟静力实验方法[4]、拟动力实验方法[5]以及振动台实验方法[6]。拟静力实验方法通过使用实验机具按照固定的加载路径对特定的试件进行加载，从而获得某种材料或构件的抗震特性。随着结构实验技术的发展，提出拟动力实验的概念。早期的拟动力实验通过数值计算来模拟结构运动产生的质量力和阻尼力，通过作动器慢速加载获得结构变形产生的恢复力。但慢速加载的拟动力实验忽略了试验子结构在地震动激励下与加速度相关的惯性力和与速度相关的阻尼力，因而只适用于惯性力和阻尼力在试验子结构中可以忽略的情况，不能用于试验子结构质量较大或阻尼项不能忽略的情况。实时混合实验[7-9]有实时加载的特点，适用于一些速率和加速度相关的构件，是当前大型结构震动测试中最为前沿的实验方法之一。振动台子结构实验是实时混合实验的一种[10]，它在传统的振动台实验中引入混合实验的思想，不仅扩展了振动台的用途，也给实时混合实验提供了新的加载装置。

通信机房中的大型走线架网阵十分复杂，而其截面皆为压制钢片或铝合金薄板，难以进行基于相似理论的缩尺设计[11]；有限元模拟针对某些非线性较强、不确定性较大的走线架部位的模拟存在困难；慢速加载的循环测试难以取代真实的走线架系统在地震动下的响应。为解决上述测试方法的缺陷，笔者将振动台与作动器联合加载的实时混合实验应用于通信设备走线架的测试领域，在一定程度上为通信设备领域复杂结构的测试提供了新的思路。

实时混合实验的关键是数值模型的实时计算及信号的实时传输，相关的解决方案包括DSpace、xpc+scramnet板卡等。为了开展实时混合实验，相关学者对实时混合实验系统进行了一系列开发和测试。Jung等[12]开发出了考虑加载系统及控制对象非线性的实验模型，该模型包含了控制器、伺服阀，执行器以及试件等部分。在该模型中，执行器和试件既可以是虚拟的数值模块，也可以替换为真实的物理结构。陈永盛等[13]提出了基于Simulink的混合实验系统，并讨论了混合实验中一系列关键性问题。王贞等[14]探讨了采用Simulink/嵌入Matlab函数模块执行复杂实时混合实验的可行性，完成了基于一种并行多步长积分算法的实时混合实验。

实时测试平台主要用于为实时硬件配置I/O通道、数据记录、激励生成和主机通讯，为一些无需专门开发相关软件、但需要对硬件状态进行实时调整与监控的项目提供了很好的选择。根据实时混合实验的需要，笔者对Simulink-VeriStand联合下的实时混合实验数值计算平台进行了介绍，并将其应用于结构的实时混合实验中。该方法结合了Simulink中函数模块矩阵运算和VeriStand实时运行的优势，能够高效率地完成实时计算任务。

Simulink-VeriStand联合下的数值计算平台的一个缺陷就是需要不断地进行数值模型的编译，不能随时修改结构参数。LabVIEW是一种图形化编程语言，是目前应用最广的图形化软件开发集成环境。为了能够方便地开展通信设备走线架的实时混合实验和仿真分析，在前一种方法的基础上，开发了基于图形化编程的实时混合实验数值计算平台。

1 实时混合实验方法

1.1 走线架系统的简化模型

提出可靠的走线架模型并确定子结构划分方法是开展走线架实时混合实验的基本前提。为了应对即将开展的实时混合实验，本节讨论走线架系统的简化方法，如图1所示。

图1 走线架示意Fig. 1 Schematic of cable tray

待测试走线架系统由铝合金走线架及走线架上方用于模拟线缆的配重块构成，其总长为5 m；走线架两端固定在随振动台运动的钢框架上，在3个4等分点处分别安装一对吊杆用于承担重力。针对以上特征，考虑将现有走线架结构的8等分点作为集中质量点，建立一个走线架系统七自由度简化模型。

走线架的总质量为配重质量与走线架自重之和，简化模型中假定总质量在整个走线架上均匀分布，7个质量点分别位于整个简化模型的8等分点处，每个质量点的质量为整个结构质量的1/8，而靠近两个边界处共1/8的质量不予考虑。在层间剪切模型中，每个自由度之间，以及最外侧自由度与边界之间的剪切刚度相同。对于该七自由度层间剪切模型，其质量矩阵为7×7的对角阵，其刚度矩阵为7×7的三对角阵，瑞利阻尼矩阵则是质量矩阵和刚度矩阵的线性组合。因此，在质量矩阵已知的情况下，只需要确定结构基频和瑞利阻尼比即可确定结构刚度、阻尼矩阵。

一个七自由度层间剪切结构可以划分为一个四自由度的数值子结构和三自由度的试验子结构，如图2所示。

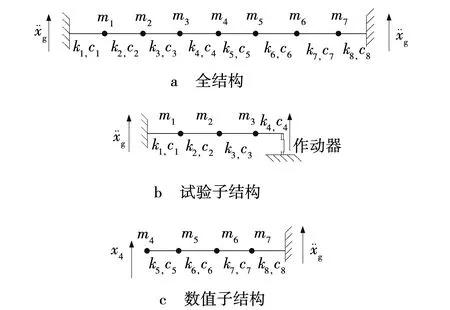
图2 简化模型Fig. 2 Simplified model

在走线架系统的实时混合实验中，数值部分的运动方程式为

MNaN+CNvN+KNdN=-MNag-RE，

(1)

式中：MN——数值子结构的质量矩阵；

aN——结构相对于地面的加速度向量；

CN——数值子结构的阻尼矩阵；

vN——结构相对于地面的速度向量；

KN——数值子结构的刚度矩阵；

dN——结构相对于地面的位移向量；

ag——地震动加速度；

RE——试验子结构的反力。

第i步的数值子结构的运动方程为

MNaN,i+CNvN,i+KNdN,i=-MNag-RE,i，

(2)

式中，i——积分步数。

1.2 实验原理

通过一个基于振动台与作动器联合加载的实时混合实验说明实验系统的工作原理。在这个实验中，用振动台来实现试验子结构受到的地震效应，用一个固定在振动台上的作动器来模拟数值部分的边界条件。具体的实验过程如下：

(1)当i=0时，假设试验子结构的反力R0=0，通过数值积分方法计算出在外荷载下数值子结构和试验子结构交界面的位移d1，并令i=1。

(2)向振动台发送第i步地震动位移，并将上一步计算出位移命令传递给电液伺服作动器对试验子结构进行加载，同时利用作动器上的测力装置测出边界处反力Ri。

(3)将测得的反力Ri传递给数值子结构，通过数值积分方法计算在Ri和外荷载激励下交界面处的位移di+1，由时滞补偿方法计算出向作动器发送的位移命令。

(4)令i=i+1，重复步骤(2)和步骤(4)直至试验结束。

1.3 时滞补偿方法

实时加载过程中，由于加载设备存在一定的响应时间，不可避免地在边界加载过程中引入时滞，时滞的存在极大地影响了混合实验的精度，因此需对电液伺服作动器进行时滞补偿[15]。

一般而言，针对作动器的时滞补偿方法主要分为两种[16]：一种是控制对象的特性随时间变化较大，需要通过外环反馈对被控对象的模型进行修正，确保作动器提前发送合适的位移；另一种是提前获得作动器的输入-输出时程曲线，并对其进行离线辨识，获得作动器的时滞或其他参数，搭建相应的补偿模块对作动器的时滞进行修正。本中选用的两种方法均属于后者。

多项式外插法是实时混合实验中最常用的补偿方法，以作动器为定时滞的动力模型作为基本假定。二阶、三阶多项式外插法的公式分别为

(3)

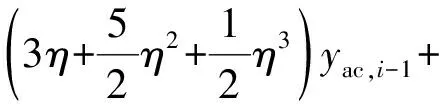
(4)

(5)

式中：τ——系统时滞；

Δt——积分步长或积分步长的正整数n倍；

yac——每隔n个积分步长向前采样一次的作动器期望位移；

yc——作动器命令位移。

逆模型法认为电液伺服作动器的位移输入-输出模型可以简化为一个二阶传递函数。参考预实验中作动器识别结果，在Simulink中搭建了相应的逆模型补偿模块。考虑到实验中噪声和逆模型中微分行为会在命令中引入大幅度高频振荡，在补偿模块后加入一个作为低通滤波器的传递函数为

(6)

式中：GIM(s)——逆模型补偿法传递函数；

GA(s)——作动器传递函数；

s——拉普拉斯算子。

2 实时混合实验系统

2.1 系统介绍

在实时混合实验的过程中，所有数值计算均在下位机机箱中的RT系统中进行。每一步数值计算完成后，相应的信号转换系统就会以电压信号的形式将补偿后的作动器位移、振动台位移传递给MTS控制器。控制器控制振动台和作动器对试验子结构进行加载并将作动器测得的反力以电压信号的形式传回PXI下位机内置的RT系统中参与下一积分步的运算，以此循环往复直至实验结束，如图3所示。

图3 走线架系统硬件平台Fig. 3 Hardware platform of cable rack system

需要注意的是，由于数值计算是在PXI下位机中完成的，因此实验中要保证PXI下位机与上位机通过网线形成可靠的连接，从而实现数值模型的载入和实验状态的实时监测。

2.2 基于Simulink的实时混合实验方法

根据1.2中提到的实时混合实验原理，编制实时混合实验程序，如图4所示。在实验模型中主要包括地震波输入模块、数值积分模块、时滞补偿模块和信号发送与接收模块4个部分。其中数值积分模块包括中心差分法[17]；时滞补偿模块采用1.3提到的多项式外插法和逆模型法；数据发送与接收模块则依托NI公司提供的In和Out模块，用户在可视化仿真软件的工具箱中可以找到。

图4 实时混合试验用可视化仿真程序Fig. 4 Visual simulation program for real-time hybrid experiment

在导入模型之前，需要在可视化仿真模型中设置相关编译环境，具体设置方法如图5所示。编译环境设置完之后，在数学软件中运行初始化文件，使软件的工作空间中有该模型中需要的所有变量。最后，按Ctrl+B快捷键进行编译，导出到相应文件夹中的.dll文件即能够在VeriStand中实时运行。

在VeriStand中建立一个新的项目或双击打开已有项目，从刚才编译出的文件夹中找出文件名与Simulink模型相同但后缀为.dll的文件并导入模型。

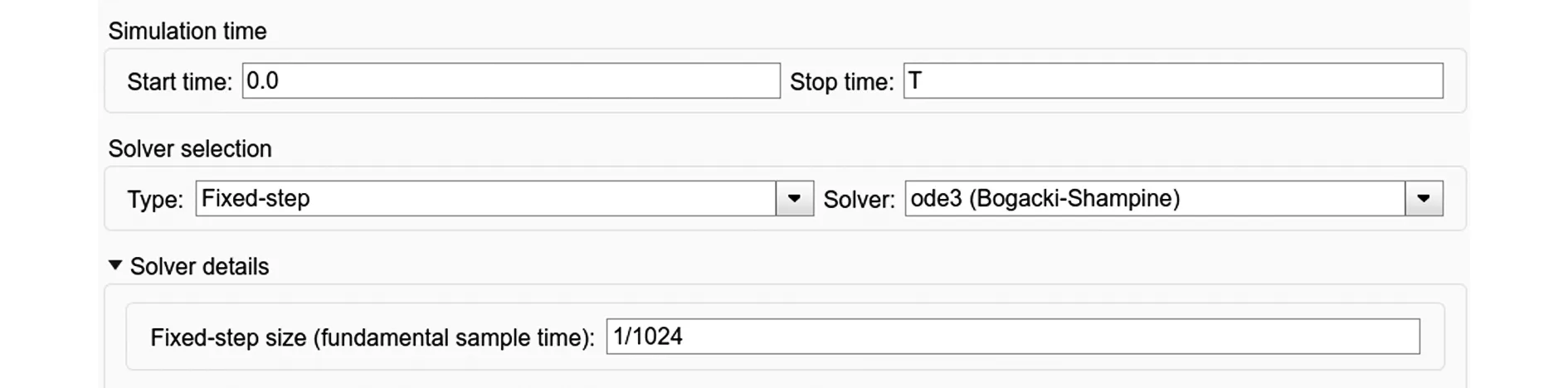
图5 Configuration parameters中参数的设置Fig. 5 Parameter settings in configuration parameters

如图6所示，在Targets-Controller中配置模型的运行环境。由于仿真模型要运行在实时控制器上，因此Targets 需要配置为Pharlap实时操作系统；IP address 中需要写入正确的下位机IP地址；随后，需根据相关要求设置相应的I/O采集频率等信息，并考虑设备的预热时间，对模型进行相应的调整。

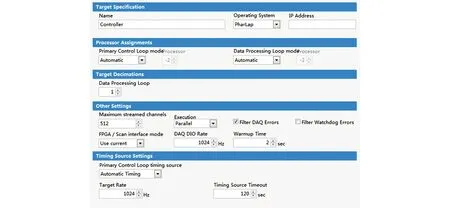
图6 在Targets-Controller中配置模型的运行环境Fig. 6 Configure operating environment of model in Targets-Controller

最终，根据要求在用户UI中设置相应的UI界面用于示波和数据记录，并进行实验的初步测试。

图7为数据传输设备示意图。实时混合实验中，数值模型通过pxie-6363板卡与MTS控制器之间的D/A、A/D信号转换系统间接控制振动台和作动器的运动。

图7 数据传输设备Fig. 7 Data transmission equipment

与数值子结构直接关联的信号传输模块为NI公司的pxie-6363板卡，该板卡设有4个输出接口及32个输入接口，在输入输出量程为±5 V的情况下担保全量程绝对精度可达1 mV以下，可以满足实时混合实验命令的收发要求。与之配套的是SCB-68A抗噪屏蔽I/O接线盒及多功能线缆。图8为该采集卡对应的设备引脚示意图。

图8 设备引脚示意Fig. 8 Schematic of device pin

实验中，通过通信板卡和导线向控制器发送经过缩放后的模拟电压信号，并接收由控制器发来的电压信号，在程序中乘以相应的换算系数，即可作为实测数据参与测试和计算。缩放可避免信号超过电压限值并防止因为电压过小而引入较大噪音。

在VeriStand中添加相应的DAQ设备后，将模型中Inports和Outports接口(对应可视化仿真模型中若干个Out 和In模块)与相应的I/O接口连接，即可将模拟信号接口与数值子结构模型相连接，从而方便数值子结构模型向外界输出电压信号并采集外界电压信号作为模型的输入，如图9所示。

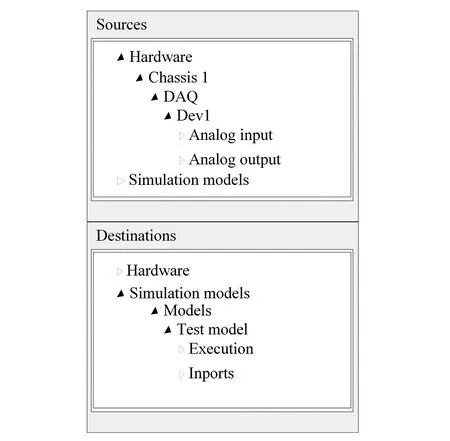
图9 物理接口连接界面Fig. 9 Physical interface connection interface

2.3 基于LabVIEW的实时混合实验方法

由于实时混合实验中作动器具有成熟的时滞补偿方法，因此实际应用时应该考虑将其编写一个固定的程序，方便主程序的阅读和修改。在LabVIEW中，这一功能是通过子vi技术实现的。子vi对应常规编程语言中被调用的脚本，用户可以将某些固定的功能用特定的子vi实现，使程序更加层次分明，易于理解。为了方便子vi在主vi中能够多次重复调用，需要在子vi的前面板点选“文件”-“vi属性”，在执行一栏中选中“预先分副本重入执行”。文中采用的作动器时滞补偿方法是多项式外插法和逆模型法。这两种方法具有较强的稳定性，适合一般的中低频加载、作动器性能较强的实时混合实验。本节在LabVIEW中实现了二阶、三阶多项式外插法，并将其作为子vi封装在实时混合实验的数值子结构模型中。多项式外插法的公式见1.3节中式(3)和(4)。在LabVIEW中，这些公式是通过一个公式节点实现的，如图10所示。

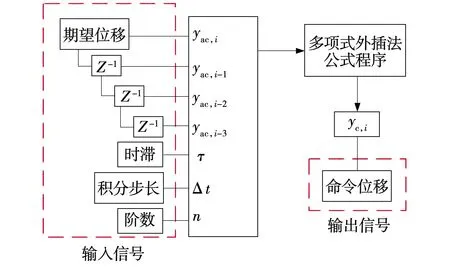
图10 多项式外插法实现过程Fig. 10 Implementation process of polynomial extrapolation

除此之外，如果需要对正整数n进行修改，则需要修改常数模块中的常量及3个反馈模块的属性。通过在前面板的下拉菜单可以在二阶多项式外插法和三阶多项式外插法之间进行切换，如图11所示。

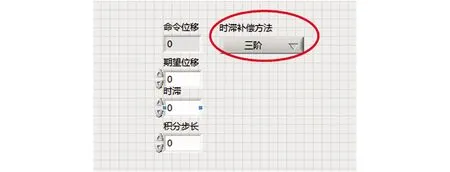
图11 多项式外插法前面板Fig. 11 Polynomial extrapolation front panel

数值积分模块中，需要引入各种算法，如中心差分法等。不同于可视化仿真等仿真工具，LabVIEW中需要在程序面板中通过定时循环或普通循环+等待函数的形式实现数值子结构的实时计算以及信号的不断发送和传递。

中心差分法的实现依托于LabVIEW中的定时循环结构，该结构可确保在算力充足的情况下结构内部的程序完成实时循环。此外，为了使积分方法的计算能够顺利进行，需要对反馈节点进行初始化，即对第0步、第-1步的初始位移进行设置。对多个自由度位移的求解则主要依托于LabVIEW中“数学”-“线性代数”选板中的矩阵函数，通过这些函数可以实现矩阵乘法、矩阵取逆等运算。

为了记录实验产生的数据，本平台中也对数据记录部分的程序进行了编制，将位移、作动器反力等数据输出为带分隔符的电子表格，支持的文件类型包括slx、txt等。实时混合实验进行完成之后会弹出对话框，用户可根据提示选择文件输出路径，点击确定之后，包括时间序列的数据就会写入到相应的文件中，如图12所示。

图12 文件输出实现程序Fig. 12 File output implementation program

基于2.2节中的硬件设备，文中编写了实时混合实验的信号输出和采集模块。信号输入输出模块分为4个子vi，其中AIinitial.vi和AOinitial.vi和DAQclose.vi三个子vi作为I/O函数初始化及结束程序放置于积分运算循环之外。而输入输出程序则放置在循环内确保每个循环都能采集到相应的模拟电压信号，如图13所示。整体程序开始执行之前，由AIinitial.vi和AOinitial.vi对硬件进行初始化配置，方便在循环中对数据的采集。在整体程序进行结束之后，会执行DAQclose.vi用于结束DAQ的输入输出任务。

图13 输入输出程序Fig. 13 Input and output program

对上述几节中的数值积分模块、信号传输模块、时滞补偿模块等程序进行整合，并添加质量、刚度、阻尼矩阵以及其他的实时混合试验必要参数的输入模块，通过图形化编程中内置的“平铺式顺序结构”和“条件结构”将这些模块整合在一起，实现了地震波读取、信号采集、数值积分运算等功能。另外，通过一个简单的状态机来控制实验的启动。本节对用户界面进行设计，帮助用户快速掌握本实时混合实验平台的使用，如图14所示。实验前，需要确定相应的积分步长以及自由度个数，并确定数值子结构的质量矩阵、刚度矩阵、阻尼矩阵等参数，选择正确的地震波文件路径。将这些参数输入完成之后，点击“开始”按钮，即可开展相应的实时混合实验或模拟工作。这一过程可表示为图15所示流程图的形式。

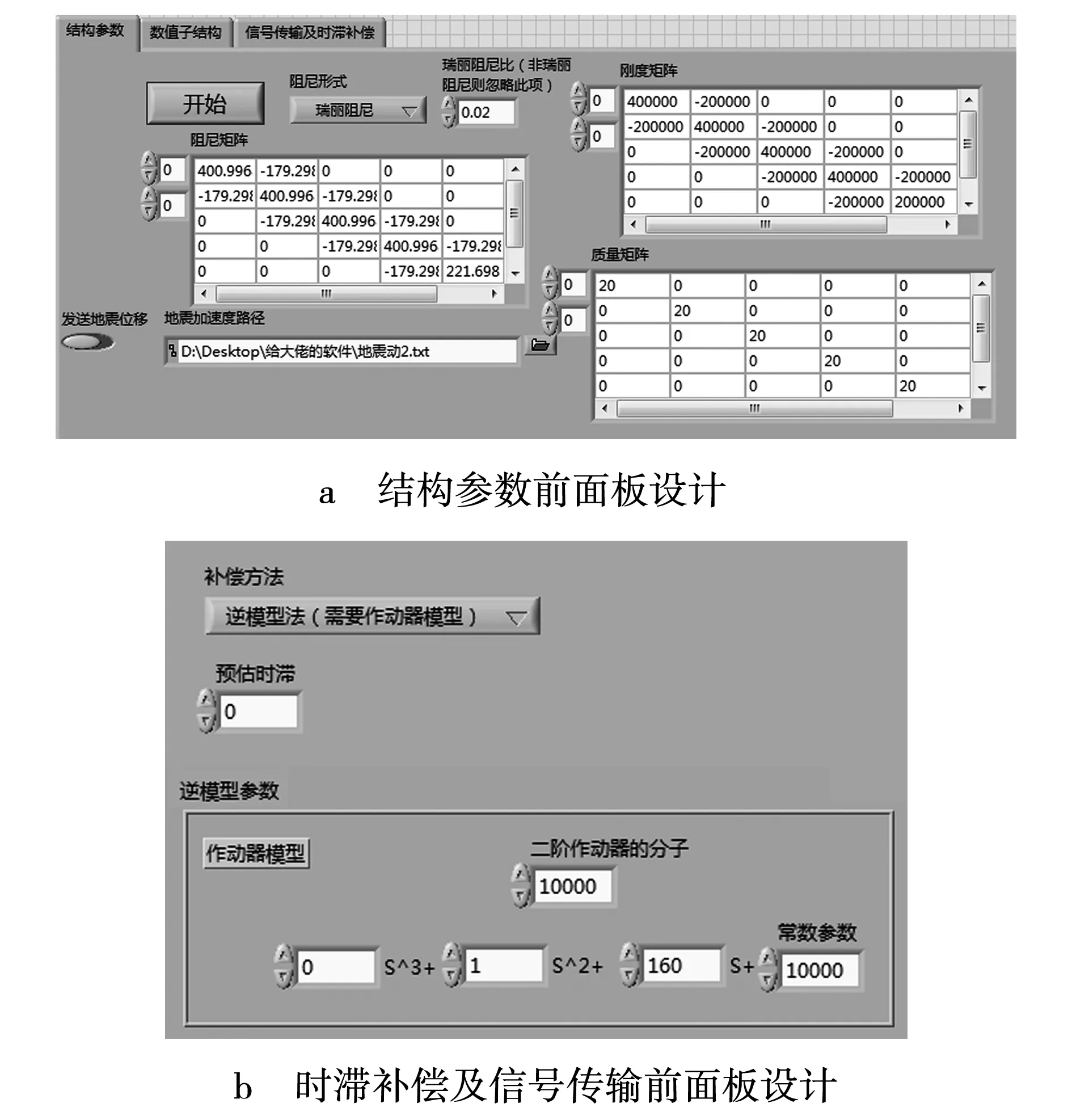
图14 文件输出实现程序Fig. 14 File output implementation program

图15 程序整体结构设计Fig. 15 Program overall structure design

基于LabVIEW的走线架实时混合实验平台与2.2节中介绍的方法一样，都能够对一般的工程结构开展实时混合测试。相比于Simulink-VeriStand联合下的实时混合试验系统，本节所开发的实时混合实验平台能够更便捷地对实时混合实验时滞补偿、数据传输中的参数进行设置，也能够随时对数值子结构参数进行修改，具有一定的便捷性。

3 实时混合实验测试

3.1 实验参数

通过一个400 mm规格的走线架结构对该实时混合实验系统进行验证。实时混合实验中，5 m长的走线架从跨中被分开，一半作为真实存在的试验子结构；另一半则作为数值子结构参与积分运算。试验子结构的一端焊接在与振动台相连接的钢框架上，另一端及其跨中用吊杆吊在钢框架的顶部。走线架数值子结构质量、刚度、阻尼矩阵分别为

3.2 结果分析

作动器的时滞补偿是本次实验的重要环节。前期的预实验结果表明，如果不进行补偿，作动器的时滞会引发位移命令的不正常振荡甚至导致试验发散。逆模型法、多项式外插法的时滞补偿效果如图16和17所示。可以看出，逆模型法能对作动器时滞进行较好的补偿，并在一定程度上改善了作动器加载幅值上的误差；多项式外插法将作动器命令提前，在需要补偿较大时滞时会产生振荡。

图16 逆模型补偿法下的位移时程曲线Fig. 16 Displacement time history curve of inverse model compensation

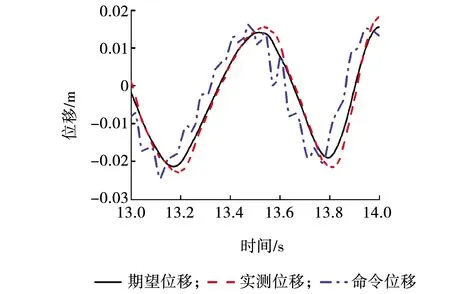
图17 多项式外插法(补偿40 ms)下的位移时程曲线Fig. 17 Displacement time history curve of polynomial extrapolation (compensation for 40 ms)

经过逆模型法对作动器进行补偿后，数值积分方法计算的期望位移和作动器实测位移基本吻合，因此认为本次实验中作动器时滞补偿取得成功。

将全结构地震模拟振动台实验和实时混合实验的位移时程曲线绘制在同一个图中，来说明实时混合实验的有效性，结果如图18所示。两条曲线的相关系数高达83.05%，说明该系统的精度较高，也验证了基于NI-MTS的实时混合实验系统具有可行性。

图18 位移时程对比Fig. 18 Displacement time history comparison

4 结 论

(1)走线架系统的实时混合实验结果表明，各模块协同工作性能正常，模块间的数据传输正确，相关系数高达83.05%，说明系统的精度较高，验证了该系统的可行性。

(2)走线架系统的实时混合实验结果与全结构实验结果对比发现，两者的吻合情况较好，验证了该系统的有效性。