无人机巡检矿区的路径规划策略

宣丽萍， 李 峥

(1.华南师范大学 数据科学与工程学院， 广东 汕尾 516600； 2.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

我国部分矿产资源储藏量处于世界前列。丰富的矿产资源是强大的综合国力的体现，但同时也给国家相关部门的监督、管理带来了不小的困难和挑战。将无人机应用到采矿领域是对该技术的一种新探索，也是对传统矿区管理技术的革新[1-2]。无人机巡检最早应用与电力行业，刘壮等[3]详细总结了近年来无人机输电线路巡检方面的研究，阐述了无人机高压线路巡检技术的应用优势及其发展现状。彭向阳等[4]提出了大型无人直升机电力巡检技术研究、装备研制和示范应用方面的实用化目标和策略。无人机电力巡检技术为其在矿区的应用提供了宝贵经验。张力等[5]设计了一种基于超声波测距的井下煤矿四旋翼巡检无人机，能够实时获取井下环境信息并通过无线网络将采集到的数据和视频信息实时回传至控制台。徐金鑫[6]对无人机露天矿区巡检控制方式进行了深入研究。综上所述，无人机在煤矿应用领域具有巨大的优势和潜能，笔者将根据某煤矿的建筑平面图，对传统蚁群算法进行改进，设计出的矿区巡检路径规划策略，通过仿真实验对比算法改进前后巡检性能的差异，验证改进后算法的优越性。

1 巡检目标路径的规划

1.1 巡检目标的确定

矿区位于安徽省境内，该煤矿围墙内工业场地占地面积为27.775 km2，其中，矿井占地面积为19.135 km2。根据图纸上标注的建筑单位及其方位信息，共选择了20个主要单位作为巡检对象，将目标单位质点化，巡检目标方位与距离信息如图1 所示。

图1 巡检目标方位Fig. 1 Patrol target orientation

1.2 数学模型的建立

巡检目标方位图确定后，需要为无人机设计一条巡视路线，从初始点出发，在多个点之间进行无人机巡航，在规定时间内返回出发点。根据上述要求需要找出合理的巡航路径，使其在规定时间内无人机巡航的点尽可能的多[7]。假设无人机可短时间垂直升空的充电四旋翼式飞行器，且对巡检时间和巡检速度等有限制。为在规定时间内巡航多个地点，要求对其路径进行科学规划达到目标函数最优，其数学模型为

(1)

(2)

式中：0,N+1——出发点和返回点(同一个点，方便模型计算)；

V——N个目标点的集合；

V0——目标和0点集合；

VN+1——无人机和N+1点的集合；

dij——i到j的距离；

Ti——到达i的时间；

xij——0或1变量，表示是否存在；

v——无人机飞行速度；

T——最大巡航时间。

由式(1)可知，其表示希望在规定时间内尽可能的巡视更多的目标地点。式(2)为约束条件，其表示使用一架无人机进行巡检，每个点最多被巡航一次，保证流量守恒，同时，巡检必须在规定时间内完成巡航任务等约束。

1.3 改进型蚁群算法的矿区巡检路径规划

针对传统蚁群算法易造成局部最优和计算时间长的不足[8-11]，在算法改进时调整思路，不要求所有蚂蚁都找到最佳路径，只要一只蚂蚁找到最优路径即可，同时，对信息素的权衡标准进行调整，借助轮盘赌算法，通过该方法及时调整不同巡检目标之间的转换状态，当某个目标适应值越高，就说明该目标地点被选中的可能性越大，最后进行较优路径结点交叉操作，当陷入局部最优时，通过来自不同目标地的路径进行交叉操作来更新路径，提高搜索效率。

利用蚁群算法进行路径规划时，构建合理的路径供蚂蚁选择，当t=0时，所有路线上均含有同等浓度的信息素。蚂蚁由目标地i移动到目标地j的概率为

(3)

式中：τij——i、j连线上的信息素量；

Ak——蚂蚁下一步可去城市的集合；

i、j——起点和终点；

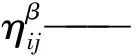
在具体运算时，假设某个路线被选定，立即重新计算信息素的分布情况，第一次巡检时将设定一个初始浓度，当一条路线巡检过之后，信息素浓度就会相应上升或下降，经反复迭代计算之后，所有目标点的浓度值均处在合理区间。初始浓度超出一定的阈值，线路更新时极易出现“早熟”现象，最快搜索到的线路有可能并不是最短的，反复搜索又会使时间增加。每次迭代后，所产生的信息素计算方法为

(4)

式中，ρ——自适应调整系数。

传统蚁群算法的实现往往容易受多种外界环境变化的干扰，引入自适应调整系数ρ优化传统蚁群算法，处理传统算法在实现时存在的收敛慢、容易产生局部循环等问题。自适应调整公式为

(5)

式中，C——随机常数。

同时，在算法改进中引入轮盘赌算法，即将轮盘算子更新方法加入到蚁群信息素转移函数中，可以提高函数收敛速度，计算方法为

(6)

式中：q——任一只蚂蚁经第k个目标至第k+1个目标中间所有的连接线的数量， 即集合i、j子区间的个数；

fij——第i个和第j个子区间解的适应度；

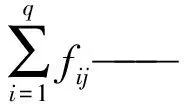
采用式(6)设定初始值C，自适应调整挥发系数ρ。改进型蚁群算法的矿区巡检路径规划具体算法步骤分为9步。

步骤1初始化蚂蚁参数M，文中设置为50只蚂蚁，新建一个50×n的矩阵作为禁忌表，其中，n为巡航点的个数，n=20，将起始禁忌表设为空集，在禁忌表中的第i行第j列的数据为o则表示第i只蚂蚁访问的第j个点为o。

步骤2生成初始解，文中设计生成种群规模为50的初始解，鉴于文中数据特点，一共有20个巡视点，首先生成一个50×20的矩阵，且每行的第一个数据为设定的出发点，在生成初始解时第一个解设置为从1到20的顺序巡视路线(除了出发点之外的19个点顺序排列)，第二条路径是从20到1的逆序巡视路线，其他的48条初始解通过将20个点随机排序生成，进行下一步操作。

步骤3构造可行解，首先将出发点加入第k行第1列的禁忌表中，初始k为1。

步骤4采用式(6)通过信息素浓度大小使用轮盘赌机制，根据信息素浓度大小作为各个点的权重判断各个节点被选择的概率，按照新状态转移概率选择下一个节点加入禁忌表，加入禁忌表中的点为下一个巡航位置。

步骤5根据式(2)判断无人机是否能够在规定时间返回出发点，从而确定蚂蚁周游是否结束，若周游结束，无人机无法在规定时间内返回出发点，则将刚选择的点踢出路径，并在路径中加上初始点用来表示无人机返回出发点，该蚂蚁的行驶路径设计完成，蚂蚁k=k+1表示为下一只蚂蚁设计路径，并返回步骤5，否则返回到步骤4继续搜索下一个点进行巡航。

步骤6判断蚂蚁k是否等于M+1，即判断是否所有蚂蚁都设计了路径，是则进行下一步骤，否则返回到步骤3。

步骤7根据式(1)计算在规定时间内巡航的点的个数，计算禁忌表中每行非零的个数再减去1，并对其排序，然后根据式(4)、(5)对选出的50条路径的巡航线路进行信息素更新，未被选中的路径也会更新信息素，未被选中的路径信息素会逐步挥发，被选中的路径次数信息素浓度增加越大，因此，下次被选中的概率也越大。

步骤8将本轮迭代的最优解跟当前最优解进行对比，若巡逻点更多，则更新最优解；若巡逻点数量相同，则比较巡逻时间，巡逻时间较少的为优。

步骤9判断是否满足结束条件，迭代次数是否达到限制，文中设置迭代次数400次；或者在规定迭代次数内最优解未发生变化，是则结束输出结果，否则进行较优路径节点交叉操作，然后判断是否满足结束条件，是则输出结果，否则返回到步骤1，进行下一轮迭代， 直至循环结束。具体算法流程如图2所示。

图2 改进型蚁群算法流程Fig. 2 Improved ant colony algorithm

2 仿真与结果分析

四旋翼无人机巡航速度为20 km/h，巡航时间未定。文中分别设定巡航5、7、10 min，对比改进型蚁群算法和传统蚁群算法的结果，分析算法的优越性。当巡检时间为5 min，出发点为1号位置时，通过改进后蚁群算法和传统蚁群算法得出结果如图3所示。从图3可知，改进后蚁群算法所获得的结果明显较传统蚁群算法的巡航路径更加简洁，巡检路线未出现交叉，从数据可以看出，在规定时间内改进型蚁群算法巡视了18个目标地，传统蚁群算法巡视目标地个数为17个，改进后算法性能更优越。

当巡检时间为7 min，结果如图4所示。从图4可知，改进型蚁群算法获得结果能巡视20个目标地，但传统蚁群算法只能巡视19个目标地，同时，改进后算法巡视总长度为2 077 m，而未改进时算法的结果巡视总长度为2 079 m，可以看出，改进型蚁群算法所求结果更加精确。

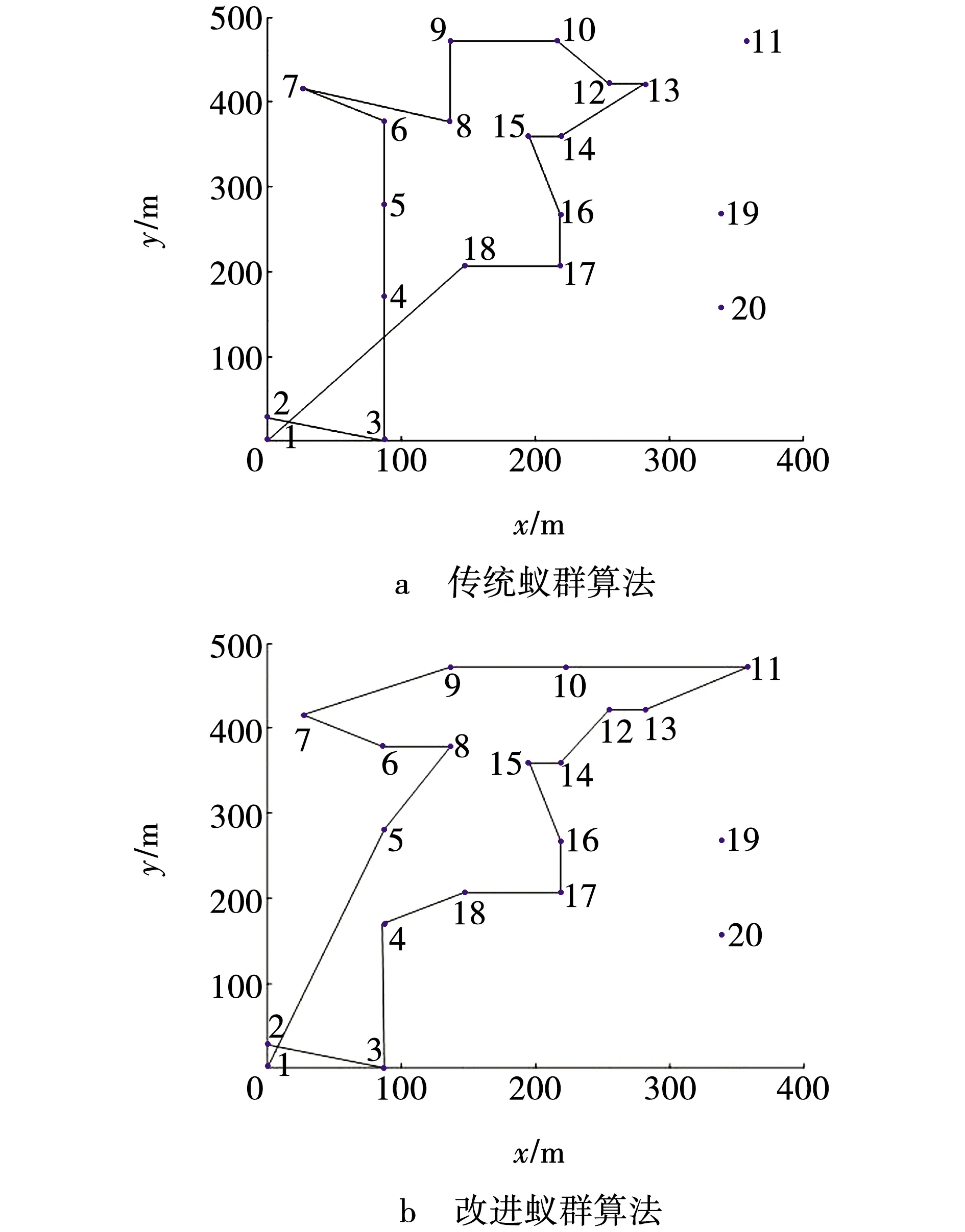
图3 5 min巡检路线Fig. 3 5 min inspection route

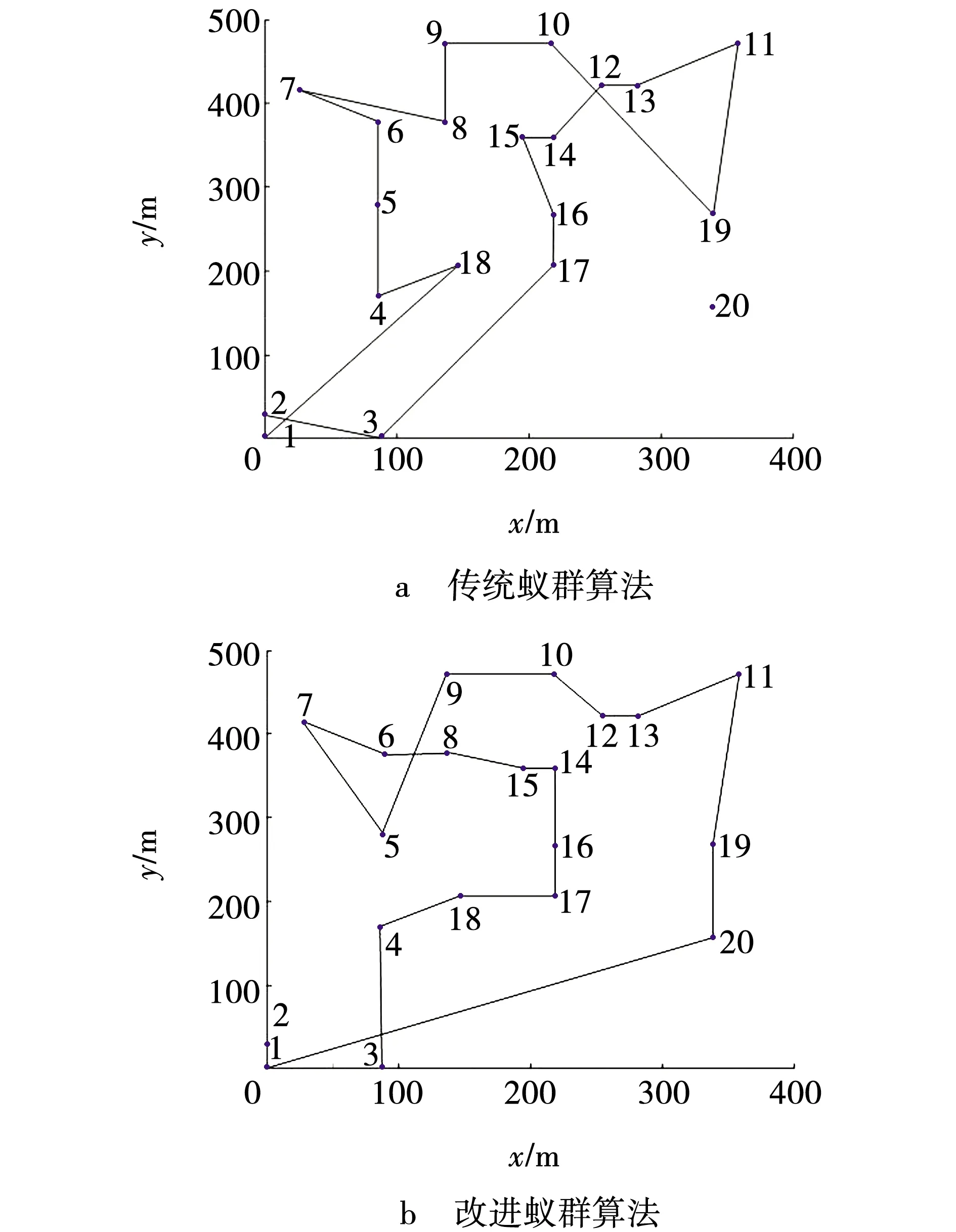
图4 7 min巡检路线Fig. 4 7 min inspection route

当巡检时间增加到10 min时，四旋翼无人机已经能做到巡检完所有地点并返回出发点，因此，此时比较的就是哪一种巡检策略能更短的时间内巡视完所有的目标地，具体结果如图5所示。

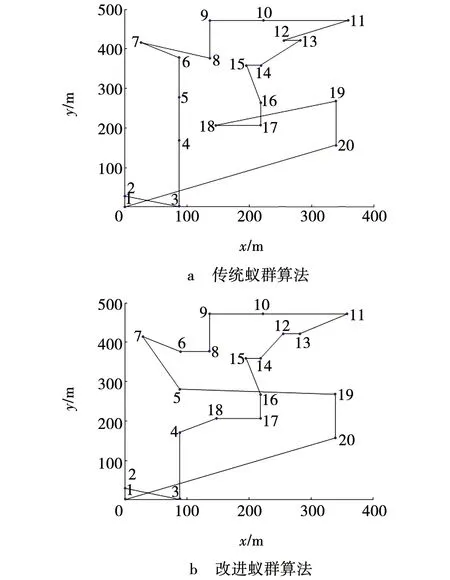
图5 10 min巡检路线Fig. 5 10 min inspection route

从图5可知，两种算法都能设计出合理路线将所有目标地巡检一遍，但是改进型蚁群算法飞行距离为2 108 m，而传统蚁群算法的路径需要飞行2 178 m。

3 结 论

(1) 当巡检时间为5 min，初始位置均为信号楼时，改进后蚁群算法所获得的巡检路线图明显较传统蚁群算法更加简洁，且算法改进后巡检路线未出现交叉，仿真表明，在规定时间内改进型蚁群算法比改进前多巡检1个目标地，综合对比改进后算法性能更优越。

(2) 当巡检时间为7 min，初始位置均为信号楼时，在规定时间内改进型蚁群算法比改进前多巡检1个目标地，同时，改进后算法巡视总长度比改进前少2 m，改进型蚁群算法所求结果更加精确。当巡检时间为10 min，初始位置均为信号楼时两种算法都能设计出合理路线将所有目标地有巡检一遍，但是改进型蚁群算法飞行距离为2 108 m，而传统蚁群算法的路径需要飞行2 178 m,改进型蚁群算法飞行距离更短。