原子层沉积技术改性CrN 硬质涂层性能的第一性原理研究

蒋钊，高恒蛟，周晖，肖更竭，成功，汪科良

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

在常用的CrN 硬质涂层制备技术中（如物理气相沉积，PVD），由于沉积温度的限制，所制备的CrN涂层会产生一定数量的面缺陷和网状缺陷，导致表面粗糙度较高，致密度较低[1-5]。随着纳米技术的发展和涂层沉积技术的进步，纳米化硬质涂层引起了越来越多的关注[6-8]。原子层沉积技术（Atom Layer Deposition，ALD）作为一种特殊的化学气相沉积技术，其利用气态源在固体表面发生化学反应，得到固体材料涂层。ALD 具有优异的三维共形性、大面积均匀性、简单精确的纳米化膜厚控制和低温沉积等优势，非常适合常规沉积技术制备的硬质涂层的表面改性和修饰[9-12]，它既可以增强涂层与基体以及各层间的结合强度，同时可以降低涂层表面粗糙度，减少涂层内部缺陷，提高涂层的致密度，进而提高硬质涂层的使用寿命，具有非常重要的实际应用价值[13-18]。

近年来，基于密度泛函理论的第一性原理计算已初步被用来进行防护涂层材料表面吸附状态、界面结合能以及微观组织结构演变等方面的研究[19-23]。从热力学角度看，原子间电负性和原子半径的差异决定了原子的密排方式，形成能量较低的晶体学结构[24]。从动力学角度看，电子的相互作用决定材料是处于低能量状态还是某一能量的动力学稳定的热力学亚稳状态[25]。但针对采用ALD 改性CrN 涂层的微观机理研究目前鲜有报道。因此，本文利用基于密度泛函理论的第一性原理计算，对ALD 表面改性CrN 涂层进行了较为系统的研究，通过建立合理的CrN-CrN 涂层复合体系模型，开展原子层沉积改性多弧离子镀CrN涂层的界面性能、弹性性能及热力学性能的仿真研究，以充分了解涂层微观组织结构演变和微观界面结构本质，为该类涂层的设计研究提供指导。

1 计算方法及模型

1.1 计算方法

本文所有优化运算工作都是通过Materials Studio模拟计算软件中CASTEP 模块完成，其计算原理以密度泛函理论为基础。采用GGA-PBE 泛函处理交换关联势能，采用超软赝势（Ultrasoft Pseudopotential）表示原子与各价电子之间的相互作用，其中N 的赝原子为2s22p3，Cr 的赝原子为3s23p63d54s1。平面波截断能取为340 eV，表面布里渊区的k格点为8×6×2，体系总能量收敛值取2.0×10−6eV/atom，分配到各原子上力低于5.0×10−2eV/nm，应力和公差的偏差要求分别小于0.1 GPa 和2.0×10−4nm。

在对材料体系进行热力学性质的模拟过程中，为了使计算模型达到平衡、稳定的状态，需要对体系的温度、压力、能量等进行调控。系综就是模拟材料体系所处的真实环境，通过固定其中的某些参数，并改变其中两个参数，来实现材料体系热学性能的有效控制。根据体系变化参量的不同，常见的系综主要有正则系综（NVT）、微正则系综（NVE）、等温等压系综（NPT）以及等温等焓系综（NPH）等。本文关于热力学性质的计算是在给定的温度下进行的，考虑在特定温度条件下，热力学平衡过程中的能量和温度波动幅度，因此材料体系的温度和体积是恒定的，选定的系综为NVT 系综。

1.2 CrN(011)面原子层数的确定

在常温常压下，CrN 为NaCl 立方面心结构，如图1 所示，其空间群为Fm3¯m。其中Cr 原子位于8个顶角和面心位置，N 原子位于两个Cr 原子中间位置。依据切面原子最多的原则，CrN 切面选择(011)面。

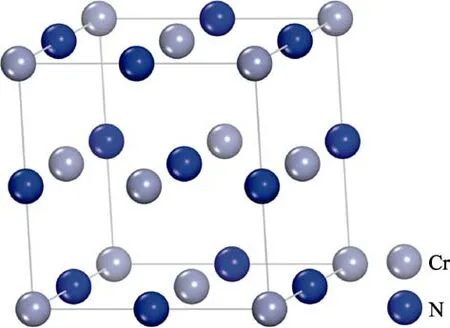
图1 CrN 晶体结构Fig.1 Crystal structure of CrN

在 CrN-CrN 复合体系模型建立之前，应确保CrN(011)平板模型包含足够的原子层数，并能够代表CrN 体相材料的性质。因此，可分别构建一系列含有不同原子层数的CrN(011)表面模型，通过计算优化后不同层数CrN 模型的能量变化，来确定合适的CrN表面层数，为后续的优化计算作准备。CrN(011)表面构型中原子层数可由公式(1)确定。

式中，ECrN(011)为不同层数CrN 模型的单原子层能量，ETotal为不同层数CrN 模型的总能量，N为模型原子层数。首先计算不同层数（2～10 层）CrN(011)模型的能量值，然后通过公式(1)计算不同层数CrN模型中单原子层的能量值，变化曲线如图2 所示。

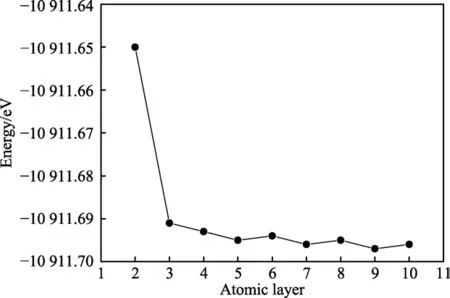
图2 不同层数CrN(011)模型能量随原子层数增加的变化趋势Fig.2 Change of the energy of the CrN(011) slab respect to the different atomic layer in CrN(011) slab

从图2 可以看出，当原子层层数N>2 时，单原子层平均能量值变化基本保持在很小的变化范围内（ΔE<0.05 eV）。因此，原子层数的变化对最终体材料性能的影响很小。为了节约计算时间，提高效率，可选择3 层CrN(011)表面模型作为计算优化的最终模型。

1.3 CrN-CrN 复合体系模型

由于原子层沉积改性的工艺过程是在多弧离子镀CrN 的基础涂层上沉积纳米CrN 改性涂层，该涂层结构可基于第一性原理分析计算涂层体系的界面性能、弹性性能和热力学性能。采用分层模型方法建立CrN-CrN 复合体系模型。依据上述CrN(011)原子层数的确定方法，当CrN(011)结构取3 层时，模拟计算已近似体材料（三维结构材料）结构性质。因此，在计算过程中建立3 层CrN 结构模型，真空层厚度为1 nm，自上而下6 层原子层分别标记为1～6 层，建立的CrN-CrN 复合体系模型如图3 所示。

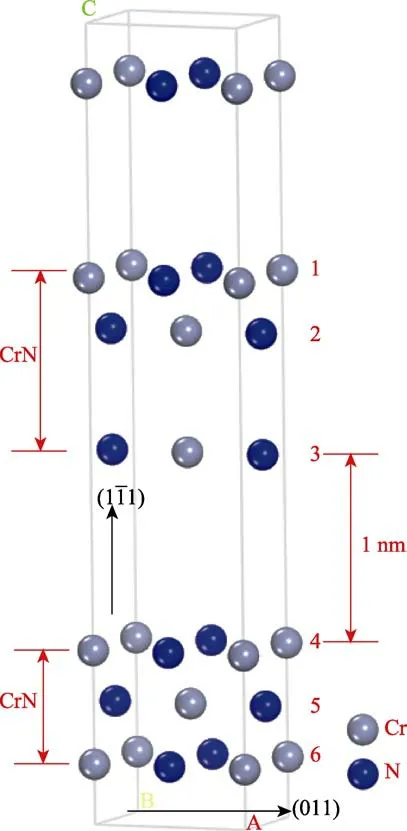
图3 CrN-CrN 复合体系计算模型Fig.3 Calculation model of the CrN-CrN system

2 结果与讨论

2.1 界面性能

2.1.1 CrN 涂层复合体系中各原子层间距变化

CrN-CrN 复合体系优化后，各原子层间间距变化如表1 所示。可以看出，各原子层间间距均有不同程度的减小，其中Δ3/4 层是预设的真空层，相当于两种涂层体系之间的界面。该原子层间距变化最大，比优化前减小了58%，优化后原子层间距接近其他各原子层的间距。依据仿真结果可以预测，原子层沉积改性的CrN 纳米涂层和多弧离子镀的CrN 涂层界面相容性很好。这是因为两种涂层体系的微观结构组织相近，对于具有高对称性的两种立方晶体，原子排列方式、间距和取向配合很好，在界面层的晶界区晶格失配度较低，原子成键强度高，由晶格位错引起的应力场很弱。所以，两种涂层体系的界面能较低，使整个涂层复合体系能量降低，结构性能稳定。

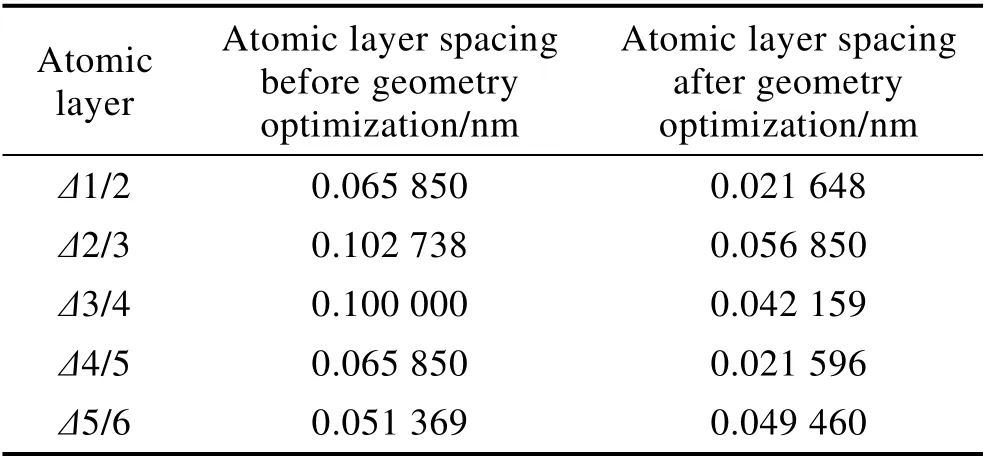
表1 优化前后各原子层距离Tab.1 Spacing between adjacent atomic layers before and after geometry optimization

2.1.2 CrN 涂层复合体系界面态密度

对建立的CrN-CrN 复合体系模型进行态密度计算，研究电子轨道的分布和成键特性。计算时以费米能级作为零势能面，计算结果如图4 所示。可以看出，在费米面附近，CrN 涂层界面间的总态密度成键能量区间大致范围为−6.4～4.8 eV，这主要为Cr 原子的3d轨道和N 原子的2p 轨道间相互作用的贡献。从Cr原子和N 原子的分波态密度图可以看出，s 轨道对导带和价带无贡献，导带和价带主要由Cr 3d 轨道和N 2p 轨道组成，N 2p 轨道和Cr 3d 轨道重叠，电子轨道通过线性组合，形成杂化轨道成键。Cr 和N 之间的电子云重叠较多，两原子的交互作用就越强，其成键能力也越强，形成的原子结构也就越稳定。

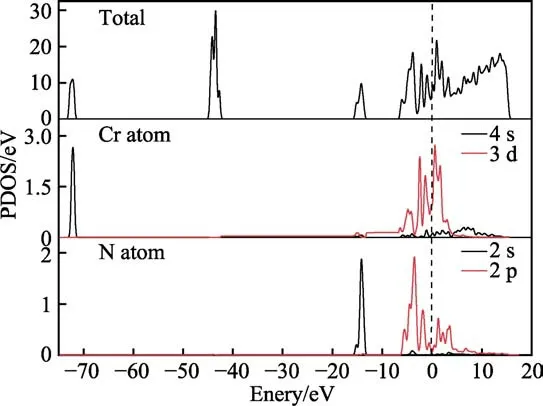
图4 CrN-CrN 复合体系界面态密度图Fig.4 Density of state of the CrN-CrN interface system

2.2 弹性性能

对于材料来说，其力学性能如弹性、塑性、硬度及强度等，均可以通过弹性常数、体模量、剪切模量和杨氏模量等数据进行判定。因此，本文通过Castep模块的应力应变关系来拟合弹性常数，从而对CrN涂层材料的弹性性能进行评判。对于立方晶系CrN而言，其平均体积弹性模量可通过公式(2)计算。

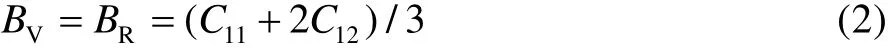
一般来说，具有更高的体积模量和剪切模量的材料具有更高的硬度，通过计算模量可间接判定材料的硬度。材料维氏硬度可通过公式(3)、(4)计算。

平均剪切模量则有2 种不同的计算方法，一种是Voigt 提出的在晶粒边界上的基于应力连续性的假设来计算的GV；另一种是Reuss 提出的在晶粒边界上的应变连续性来计算的GR。而实验上得到的G一般为GV和GR的算术平均值，如式(5)—式(7)。

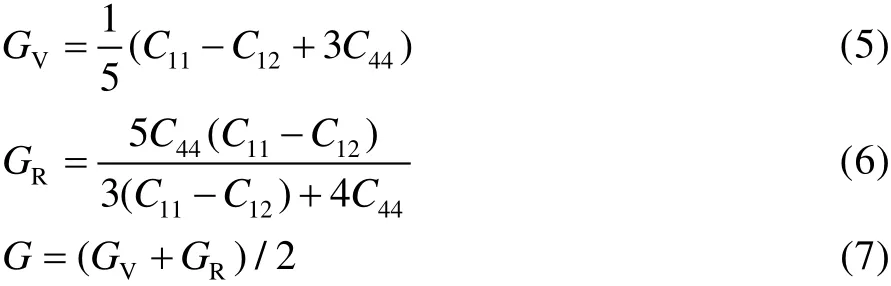
式(5)、(6)中，C11、C12和C44为弹性常数，描述应力和应变之间的关系，是应力对应变展开的线性项，对于对称性最高的立方晶系，有3 个弹性常数。模拟计算后得到的CrN 涂层的体弹性模量、剪切模量等力学性能数据如表2 所示。由于实验测量的G使用的是多晶样品，包括缺陷和孔洞，而本文计算的则是完整规则的晶体，因此得到的数值与实验值略有差异。

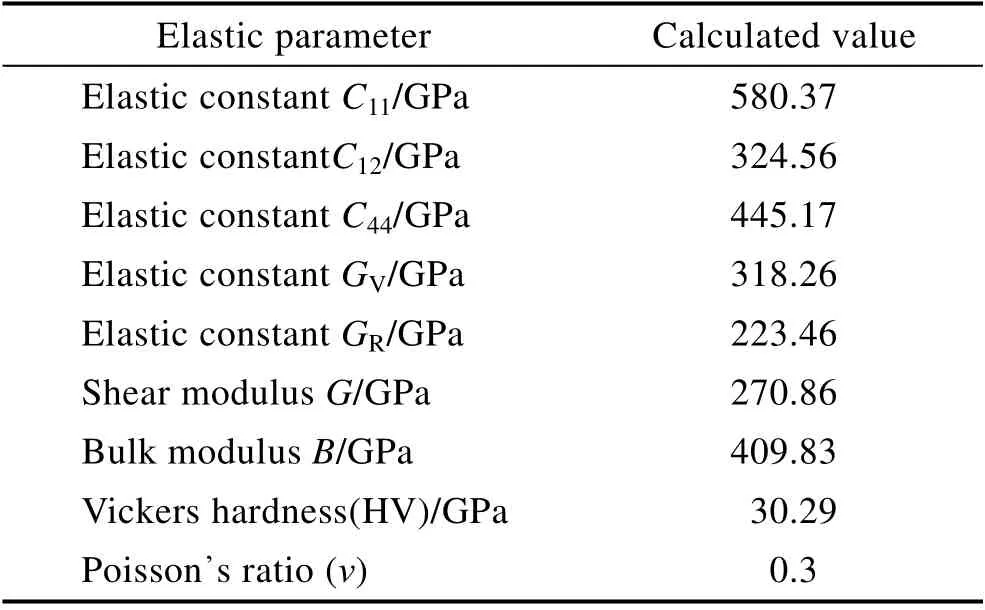
表2 CrN 改性涂层弹性计算结果Tab.2 Calculated elastic result of the modified CrN coating

机械稳定性是晶体存在的重要条件。对于立方晶体，其弹性常数应该遵循波恩准则的判定依据：C11>0，C44>0，C11>C44，C11+C44>0。表2 中计算得到的CrN涂层的弹性常数值均满足以上的稳定性条件。因此，其机械性能是稳定的。其中，与实际测试力学性能物理量直接相关的是维氏硬度和体积模量，分别为30.29 GPa 和409.83 GPa，模拟计算结果符合CrN 硬质涂层实验测试值范围，可作为CrN 涂层设计和评价的依据。

2.3 热力学性能

通过设定不同温度，对CrN 复合模型体系进行耐受温度和能量的收敛计算，可以得出CrN 涂层在不同温度下耐受温度和能量的变化规律。通常认为，如果在设定的温度下能量曲线收敛，说明在此温度下CrN 涂层工作稳定；如果在设定的温度下耐受温度发生突变而不收敛，则认为在该温度条件下涂层体系已经热分解失效。

CrN-CrN 复合体系模型作为热力学仿真模型见前文图3。热力学性质采用NVT 系综模拟，模拟温度分别为773、873、973、1023、1073 K，让所有原子弛豫，考虑其动态情况，模拟时间为0.5 ps，时间步长为1.0 fs。在不同的温度热力学模拟过程中，耐受温度及能量变化分别如图5 和图6 所示。

从图5 温度变化曲线可以看出，当模拟温度T≤1023 K 时，温度波动都在一定的振荡范围内收敛。在模拟过程初期，温度都是快速下降，到一定的数值后开始出现循环振荡。在振荡过程中，773、873、973、1023 K 温度条件下最低振荡温度依次为259.3、250.5、306.7、433.8 K，最高振荡温度依次为590.2、710.9、813.2、888.6 K，温度振幅为330.9、460.4、506.5、454.8 K。不同温度条件下，温度振荡范围越大，CrN内部电子热振动现象越明显。当T≤1023 K 时，模拟过程中温度始终振荡收敛，可以认为在此温度条件下CrN 涂层未分解失效，结构稳定存在。当模拟温度为1073 K 时，在模拟过程的某个时间点，温度瞬间激增，温度振荡不再收敛，可以认为在此温度条件下CrN 涂层已经热分解开始失效，涂层不适宜在此温度下使用。因此，CrN 涂层的工作极限温度为1023 K。

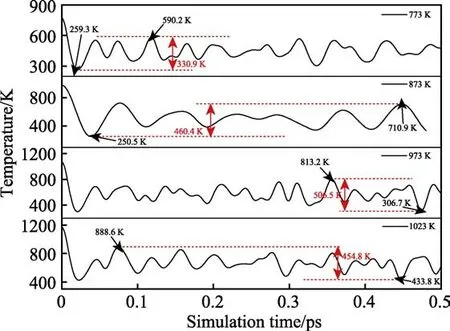
图5 不同温度下CrN-CrN 复合体系的耐温温度曲线Fig.5 Temperature resistance curves of the CrN-CrN system under different temperature settings

从图6 的能量振动曲线可以看出，对应不同模拟温度下体系能量的振幅分别为0.059、0.034、0.018、0.047 eV。能量波动均包括三个阶段，即：初期的振荡阶段、中期的快速变化阶段和后期的振荡收敛阶段。在最终的收敛阶段达到了体系电子能量振动平衡状态。当温度T>1023 K 时，体系能量在某个时间点瞬时激增，不再收敛，从而认为在该温度下，CrN 涂层不能稳定存在，将发生热解。

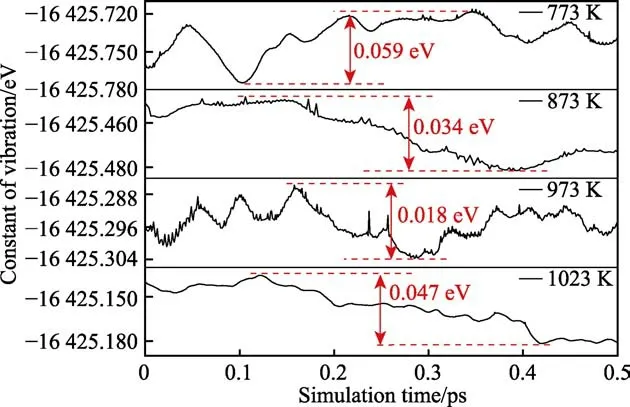
图6 不同温度下CrN-CrN 复合体系的能量振动曲线Fig.6 Energy vibration curves of the CrN-CrN system under different temperature

3 结论

1）CrN-CrN 复合体系界面模型经过优化后，各原子层间间距均发生不同程度的减小，且各层间距趋于一致，可以预测原子层沉积改性的CrN 纳米涂层和多弧离子镀的CrN 涂层的界面相容性很好，这是因为界面处原子成键强度高，结构性能稳定。界面间成键能量为−6.4～4.8 eV，成键主要来自于Cr 原子3d轨道和N 原子2p 轨道间的相互作用。

2）经过理论计算，CrN 涂层弹性常数满足波恩准则判定依据，其力学性能稳定。在此条件下模拟计算的CrN 涂层硬度为30.29 GPa，体积模量为409.83 GPa，剪切模量为270.86 GPa，可作为CrN 涂层设计和评价的依据。

3）当温度T≤1023 K 时，温度波动振荡收敛，当温度T>1023 K 时，温度在某个时间点瞬时激增而不再收敛，通过热力学仿真可以得出CrN 涂层的极限使用温度为1023 K。