股市截面收益的异常变量：一个文献综述

吴辰星，赵永亮

（盐城工学院，江苏盐城 224007）

引言

在Markowitz（1952）[1]现代资产组合理论（Modern Portfolio Theory）的基础之上，Sharpe（1964）[2]、Litner（1965）[3]和Mossin（1966）[4]相继推导出了资本资产定价模型（Capital Asset Pricing Model），该理论作为传统金融体系的核心为学术界所悉知。CAPM 理论的核心思想在于其认为“理性人”都会持有市场组合，因而公司个别风险在市场组合中都将被对冲掉。因此，市场仅仅应当给予股票中那部分无法被分散的系统性风险（即贝塔系数）以价格补偿，而不应当给予公司层面的风险以报酬。然而，随着股票市场实证研究的不断扩展和深入，研究者发现大量可观测到的公司特点能够作为股票横截面收益的预测因子（Fama，1998[5]；Mclean and Pontiff，2016[6],等），这就是所谓的股票定价“异象”（Anomalies），这些股市截面收益的预测因子也可以称为异常变量（Anomaly Variables）。关于股票定价异象的研究可以回溯到Ball 和Brown（1968）[7]以及Blume 和Husic（1973）[8]的早期研究。然而，几十年过去了，学术界仍然无法对究竟哪些异常变量可以预测股票收益，以及引起这些股票收益异常的可预测性原因这两个问题达成共识。

本文对国内外与股市截面收益异常变量相关的文献进行了系统梳理，并归纳了截面收益异常变量的检验方法，对异常收益产生的原因进行了分析和阐述，最后指明现有研究的不足之处，并提出今后的研究方向。

一、国内外股市截面收益异象变量的类型

国内外关于异象变量的研究主要从横截面和时间序列两个角度出发。本文的研究内容为截面收益异常变量，因此对于从时间序列角度出发的异象变量研究不做赘述。本文总结了20 篇学术文献中指出的20个对股市横截面收益具有预测性的变量。这些文献的发表时间跨度近40年，最早的为1973年，最新的为2011年。表1 中为这些异常的股票收益预测因子。所涉及的预测因子大致可以概括为四种类型。第一种预测因子有很强的理论基础且已经被列入定价模型，如Fama和MacBeth（1973）[9]提出的市场风险因子贝塔系数和Fama和French（1992）提出的账面市值比因子。第二种预测因子是根据股票的交易数据计算得出的，如Amihud（2002）[10]提出的流动性因子。第三种预测因子是根据公司基本财务指标计算得出的，如Cooper、Guylen 和Schill（2008）[11]提出的资产增长指标。第四种预测因子为行为金融学中的股票价格异象因子，如Jegadeesh 和Titman（2001）[12]提出的动量效应指标。

国内学者所研究的股市横截面收益预测因子基本上可以囊括在上述的四种类型因子之中。早期的研究集中于第一种类型和第三种类型的因子，如直接采用Fama-French 三因素模型框架，或者Carhart 四因子模型（在三因素模型的基础上加入第四类因子中的动量效应因子）对中国股市数据进行实证检验（如施东晖，1996[13]；靳云汇和刘霖，2001[14]；朱宝宪和何治国，2002[15]；吴世农和许年行，2004[16]；朱波和宋振平，2009[17]等）。潘莉和徐建国（2011）[18]用市盈率替换了账面市值比，构建适用我国股市的新三因素模型。近期的研究则集中于Fama-French 五因子模型在中国股市的检验（如余立威，陈涛，2017[19]；杜威望，肖曙光，2018[20]等）。关于第二种预测因子的研究在国内也比较常见，如苏冬蔚和麦元勋（2004）[21]、张峥和刘力（2006）[22]用换手率来衡量流动性，并得出了换手率与期望收益的负相关关系。田利辉、王冠英（2014）在Fama-French 三因素模型的基础上构建了包含成交额和换手率的五因素定价模型。至于第四种类型的预测因子，由于行为金融学中大多数的股票价格异象是在时间序列的基础之上展开的，因此对于行为金融方面的异象预测因子研究集中在动量效应因子、反转效应因子和投资者情绪因子（如胡汝佳，2013；王浩，李晓帆，陈伟忠，2018，等）。

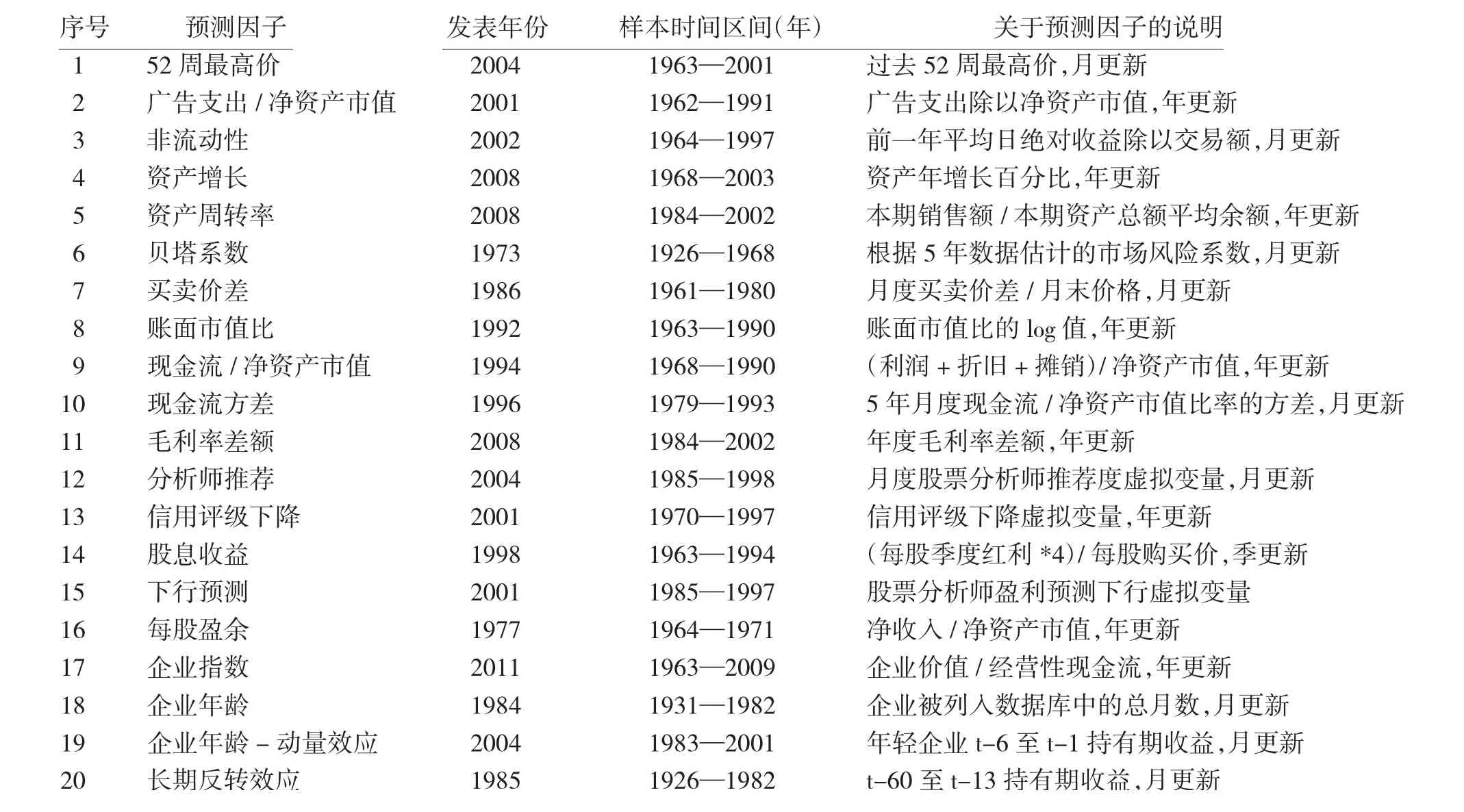
表1 异常的股票收益预测因子

二、截面收益异常变量的检验方法概述

国内外对截面收益异常变量的检验方法主要是沿用Fama-French 三因素模型所采用的分组检验法。首先构建多空组合（Long-short portfolios）。对于一些异象变量，如动量效应因子，异象变量值越高，异象收益值越大；而对于另外一些异象变量，如企业规模，异象变量值越大，异象收益越小。构建多空组合指的是针对每一项异常因子构建等权重加权投资策略组合。研究的基本思路是在确定的时间区间内，把股票根据某一异象变量值（如非流动性指标）的大小逐月进行排序，并将排序后的上市公司分为五等分，分别构建成投资组合（投资组合内的股票是按月更新进行调整的）。将在异常变量或预测因子作用下具有更高收益的投资组合称为异象多方，反之则称为异象空方。对于异象变量中的指标型变量（如信用评级下降），则要根据指标型变量的值（如0 或1）构建异象多方或者异象空方组合。比如，如果该指标型变量值为1 时异象收益更高，则该指标型变量值为1 的股票将构成异象多方投资组合，其余的股票将构成异象空方投资组合。反之，如果该指标型变量值为1时异象收益更低，则该指标型变量值为1 的股票将构成异象空方，其余的股票将构成异象多方。做空异象空方，做多异象多方、将构成多空组合。然后，计算多空组合收益率并进行T 检验。采用月度数据进行分析，分别计算每一个异象变量空方组合和多方组合在某一时间区间内的等权重加权平均月度收益率（组合中的股票加权平均）。多空组合的收益率，又叫做异象收益，为多方组合收益率减去空方组合收益率。对异象收益进行T 检验，以判断该异象变量是否显著。

三、国内外异象收益可预测性的产生原因

国内外有三种关于股市横截面收益可预测性的解释比较普遍。

第一种观点认为，收益可预测性来源于风险的差异（如Fama，1991，1998；杜威望，肖曙光，2018，等）。换句话说，这些异象收益实际上是风险溢价。在这种解释框架下，横截面收益可预测性的产生实际上是并不属于真正的“异象”，因为这些预测因子实际上反映了用来给股票定价的折现率。

第二种观点认为，回报的可预测性是一种错误定 价（Mispricing）（Barberis 和Thaler，2003；Bradshaw，Richardson 和Sloan，2006；胡汝佳，2013；Engelberg，Mcleanh 和Pontiff，2018；Fahad，2018，等）。根据错误定价假说，投资者会对一部分股票未来的现金流期望过分乐观，而对另一部分股票的期望则过分悲观，异常变量正和这些期望偏差相关。当新信息以公司盈利公告或者其他的形式出现时，投资者会更新他们的期望，从而引起股票价格的更正，因而产生了收益的可预测性。

第三种观点认为，收益可预测性可能是因为“数据挖掘”。Fama（1998）指出，学者们检验了成千上万的变量，因此，即使找到一些变量在其样本中可以预测收益也不足为奇。况且在现实中，这些变量根本无法预测股市的收益。

四、总结性评论及对中国的研究展望

近几十年，股市的异常变量引起了国内外学术界以及投资者的广泛关注。现有的与股市截面收益的异常变量相关的文献，为我们进一步研究股价的波动提供了丰富的材料和深刻的见解。诚然，国际上关于股市异象变量的实证研究已经相对完善，但其研究发现却未必能够适用于中国股市。一方面，我国股市从微观上来说具有散户投资者众多、机构投资者同质化的结构特点，因此非理性交易与投机行为相对于美国股市而言要普遍得多（田利辉，王冠英，2014）。正是这些非理性交易者的大量存在，使得部分在他国市场上通行的收益预测因子，如Fama 和French（1992）提出的三因素模型中的价值因子，在中国股市就无法适用（Chen，Hu，Shao 和Wang，2015）。此外，Mcleanh 和Pontiff（2016）通过对美国股市的研究发现，投资者会从学术文献对异象收益的报告中学习和调整投资策略，从而降低美国股市的错误定价水平。若借鉴其研究思路，将其运用到中国股市，则可以通过数据的对比反映出中美股市投资者理性水平是否存在差异。另一方面，中国股市的卖空限制程度要高于美国。胡汝佳（2013）认为，中国股市的异象收益并非来源于投资者非理性，而是由于卖空限制过高，使得市场上长期存在部分价值被高估的股票。也就是说，股票市场政策及其他特点的差异，可能会导致异象收益产生原因的差异。综上所述，未来进行更多针对中国股市数据进行相对完善的异常变量的实证检验研究，并在此基础上结合中国股市政策分析异象收益可预测性产生的原因是十分必要。