基于IERT的非线性全光谱复杂水体定量分析算法研究

刘嘉诚，胡炳樑，于 涛*，王雪霁，杜 剑，刘 宏，刘 骁，黄琦星

1. 中国科学院西安光学精密机械研究所光谱成像技术重点实验室，陕西 西安 710119 2. 中国科学院大学，北京 100049 3. 深圳市盐田港集团有限公司，广东 深圳 518081

引 言

人类的行为活动会对地球生存环境构成重大威胁。据研究，全球所有死亡人数中有23%是因为环境因素[1]。对人类生存环境的研究、保护和治理刻不容缓。水是自然环境和社会环境中极为重要且活跃的因素，对水质信息的科学监测是实现水资源优化配置与高效利用的基础。水质监测中常用到的指标包括化学需氧量(chemical oxygen demand，COD)、生化需氧量(biochemical oxygen demand，BOD5)、总有机碳(total organic carbon，TOC)、硝酸盐氮(NO3-N)、浊度(turbidity)、色度(colority)等。通过这些指标的监测，可以反映当前水体中各种污染物的浓度及变化趋势，从而达到评价水质状况的目的。

常用的水质监测方法多为基于化学检测的方法，包括现场取样进行实验室化学检测和利用基于化学法的仪器进行原位监测。现场取样进行实验室化学检测非原位、周期长，难以实现在线监测； 基于化学法的仪器由于其使用化学试剂，存在化学残留，容易导致二次污染。近年来，基于光谱法的水质监测技术由于无需化学试剂、无二次污染、快速准确、成本低的特点，可实现实时在线原位测量，已广泛应用于在线水质监测领域。光谱法水质监测技术是利用水中特定物质吸收特定波长的光，产生分子吸收光谱，通过建立预测模型，根据测得的吸收光谱来定性定量地分析水质参数。

光谱法水质监测中常用的预测模型主要分为线性模型和非线性模型，线性模型主要包括单波长法、多波长组合法、偏最小二乘(partial least squares, PLS)等。Dogliotti等利用645 nm波段与859 nm波段的单波长半分析方法来反演水体浊度[2]； Knaeps等利用1 020 nm波段与1 071 nm波段分析水体总悬浮物[3]； Carreres-Prieto等利用多元线性回归(multivariable linear regression，MLR)预测COD等[4]； PLS是由Wold提出的一种多元线性回归方法，它通过不断提取主成分来简化数据，建立回归模型，王莉丽等将PLS用于水体化学需氧量的测量并取得了不错的效果[5]； Wang等使用PLS和多种机器学习算法预测水体总氮含量[6]。非线性模型主要包括支持向量机(support vector machines, SVM)，神经网络，决策树等。SVM是由Vapnik提出的一种非线性回归方法，它将低维数据映射到高维空间进行回归，再把高维空间的超平面映射回低维空间，建立回归模型，陈颖等人将SVM的改进方法用于水体硝酸盐浓度的预测[7]； Gu等使用随机森林(random forest，RF)的方法预测河流水体浊度[8]； 神经网络是一种仿生的计算方法，用于大规模非线性的系统建模，Charulatha等将人工神经网络(artificial neural network，ANN)用于地表水的亚硝酸盐检测[9]； Chen等使用近红外光谱结合卷积神经网络(convolutional neural networks, CNN)检测农业灌溉用水[10]。

单波长、多波长的组合方法都依赖于水体对特定波长的吸收特征，同一波长组合建模可能适应于特定应用场景，不具有普适性。PLS算法虽然利用了全光谱的数据，但只能寻找线性特征进行回归，无法捕捉非线性的特征。SVM算法对小样本的学习和预测性能较好，但惩罚参数的选择对模型精度影响较大，惩罚参数较大模型容易过拟合，惩罚参数较小模型容易欠拟合。基于神经网络的算法对样本的数量需求较高，在小样本情况下模型泛化能力较差，且模型训练时间长。

1 算法原理

1.1 算法基本原理

为了解决上述问题，引入机器学习中极端随机树的思想，提出了一种基于改进极端随机树(improved extremely randomize trees，IERT)的非线性全光谱浊度定量分析算法。极端随机树(extremely randomize trees，ERT)是由Pierre Geurts等学者提出的基于决策树的集成方法，用于解决机器学习中的监督分类和回归问题。该方法对高维特征数据能很好的处理，准确度高，且能够并行计算，执行效率高[11]。由于精细光谱数据的高光谱分辨率导致的数据量大、不同波段之间数据存在冗余等特点，采用核主成分分析(kernal principal component analysis，KPCA)方法进行特征降维，通过非线性函数把吸光度光谱映射到高维空间进行主成分分析，提取数据高维、非线性的特征。之后，正态化降维后的数据，训练基于IERT的非线性全光谱浓度预测模型，算法流程图如图1。

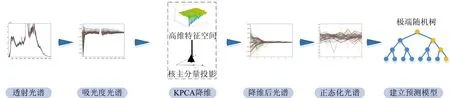
图1 IERT算法流程图Fig.1 Flowchart of IERT algorithm

1.1.1 吸光度转换

实验室测得的水体光谱为透射光谱，首先应转换为吸光度光谱，转换方法如式(1)所示。

(1)

式(1)中，I1为被测水体的透射光谱，I0为标准去离子水的透射光谱，A为吸光度光谱。

1.1.2 核主成分分析

核主成分分析方法是一种非线性的数据降维方法，它利用投影子空间技术，将信号非线性的映射到特征空间，在特征空间中对转换后的信号运用线性主成分分析进行数据降维，再将降维后的数据投影回输入空间，其中的非线性映射必须是可逆的。

根据KPCA算法的原理，将其用于吸光度光谱特征降维的流程如图2。

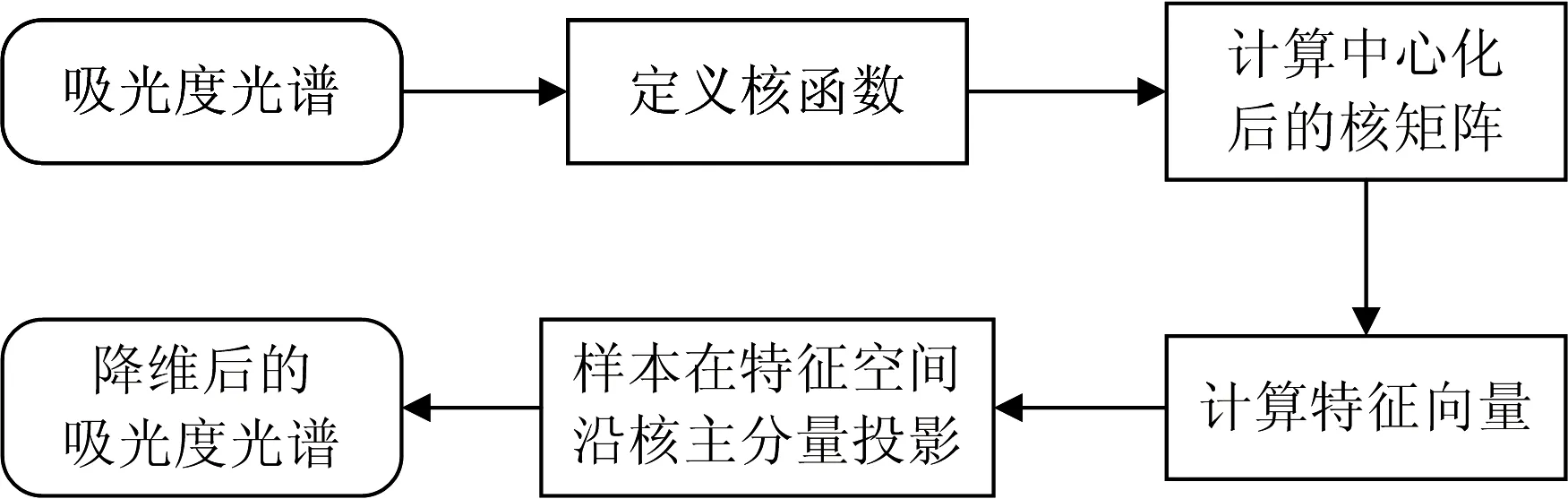
图2 KPCA算法流程图Fig.2 Flowchart of KPCA algorithm

首先，针对转换后的吸光度光谱，定义核矩阵K。

(2)

最后，计算样本在特征空间上的投影，即为KPCA降维后的吸光度光谱。

1.1.3 数据正态化

数据正态化是为了让数据服从标准正态分布。假设KPCA降维后的吸光度光谱为X, 它服从均值为μ、方差为σ的正态分布。则数据正态化的计算公式如式(3)所示

(3)

式(3)中，S为正态化变换后的数据，服从均值为0，方差为1的正态分布。

1.1.4 极端随机树

决策树(decision tree，DT)是一种分类、回归模型，具有较高的可解释性和鲁棒性[12]。极端随机树是一种基于决策树的集成方法，它由很多棵决策树组成，且每一棵决策树之间没有关联。极端随机树在树节点分割时随机化切割点的选择，随机化的强度可以根据不同问题的需求，通过调节参数的方式来改变[13]。极端随机树使用所有的训练样本得到每棵决策树，组合成为模型，当有一个新的样本输入的时候，让模型中的每一棵决策树分别进行判断。与其他机器学习算法相比，极端随机树除了高准确性之外，还具有高计算效率的优势。

极端随机树算法根据经典的自上而下方法构建一组“自由生长”的决策树或回归树，与其他基于树的集合方法有两点不同： 不同于随机森林在一个随机子集内得到最佳分叉属性，它选择分叉的特征属性时是完全随机的； 它使用整个学习样本来得到每棵决策树[14]。

极端随机树的实现流程如图4所示。

图3 实验装置示意图Fig.3 Schematic diagram of experimental device

图4 极端随机树算法流程图Fig.4 Flowchart of extremely randomize trees algorithm

1.2 模型评价标准

1.2.1 决定系数

决定系数(R-Square，R2)反应了因变量的全部变异能通过回归关系被自变量解释的比例。决定系数越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比越高，观察点在回归直线附近越密集。如R2为0.9，表示回归关系可以解释因变量90%的变异，R2越大，表示模型的拟合效果越好。R2的计算公式如式(4)

(4)

1.2.2 均方根误差

均方根误差(root mean squared error，RMSE)是衡量平均误差的方法，可以评价数据的变化程度，均方根误差越小，说明用该预测模型描述实验数据的准确度越高，RMSE的计算公式如式(5)

(5)

2 实验与结果讨论

2.1 仪器与数据采集

实验室数据采集方法如图3所示，实验装置主要由光源、精细光谱分析仪和采集软件组成。

其中光源采用氘卤二合一光源，它在一个通道里整合了连续的氘灯和卤素灯宽波段光谱，波长范围190～2 200 nm，预热时间40 min。光路采用抗紫外辐照石英光纤，纤芯直径600 μm，波长范围185～1 100 nm。比色皿采用石英比色皿，光程10 mm，适用波长185～2 500 nm。光谱仪采用项目组自主研发的光谱分析仪，如图5所示。

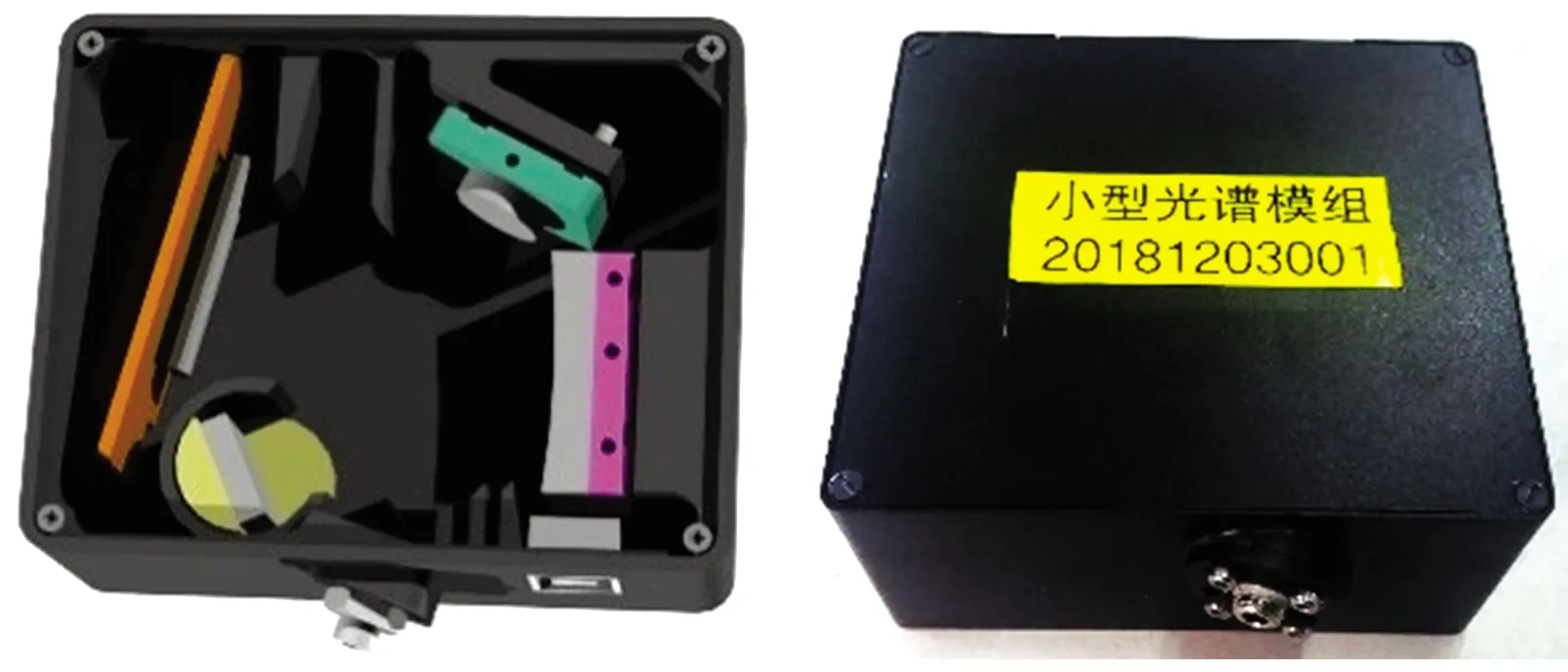
图5 光谱仪模型图及实物图Fig.5 Model diagram and physical diagram of the spectrometer

该光谱仪采用了连续谱精细获取技术，整个仪器采用了双光路矫正，采用特征点领域多波长位置实现大量程适应性调节，其光谱范围为185～1 100 nm，光谱采样间隔为0.45 nm。

使用本套实验装置，对光源进行5 h连续测量，得到本系统稳定性为2.38%。

2.2 实验数据

使用实验室配置的多组分混合溶液来模拟复杂水体，为了避免本算法只对特定的混合溶液有效，使本算法所建立的非线性全光谱浓度预测模型具有普适性，且克服水体混浊度、色度等对光学测量有严重干扰的影响因子，实验数据选取了两组不同的多组分混合溶液，分别为200组COD，BOD5和TOC多组分混合溶液与188组NO3-N、浊度、色度多组分混合溶液。

2.2.1 COD，BOD5，TOC多组分混合溶液数据集

采用国标方法，用邻苯二甲酸氢钾、谷氨酸和葡萄糖配置200组不同浓度的COD，BOD5，TOC混合溶液，如表1所示。

表1 COD，BOD5，TOC多组分混合溶液数据集样本特性表Table 1 The sample characteristics table of multi-component mixed solution dataset of COD, BOD5 and TOC

将200组样本随机分配，取其中40组为测试集，其余160组为训练集。

2.2.2 NO3-N、浊度、色度多组分混合溶液数据集

实验室采用国标方法，用硝酸钾、硫酸肼、六次甲基四胺、六氯铂酸钾和六水氯化钴配置188组不同浓度的NO3-N、浊度、色度混合溶液，如表2所示。

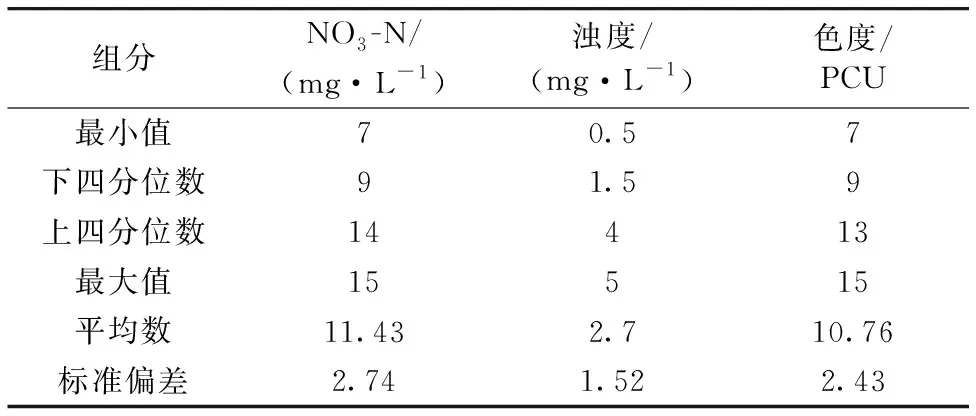
表2 NO3-N、浊度、色度多组分混合溶液数据集样本特性表Table 2 The sample characteristics table of multi-component mixed solution dataset of NO3-N, turbidity and colority

将188组样本随机分配，取其中38组为测试集，其余150组为训练集。

2.2.3 多组分混合溶液光谱数据采集

采用上述实验装置，在室温[(25±1) ℃]条件下对配置的样本进行透射光谱的测量，每个样本扫描10次，取平均值作为该样本的测量值。COD，BOD5和TOC混合溶液的透射光谱如图6(a)所示，NO3-N、浊度、色度混合溶液的透射光谱如图6(b)所示。

图6 多组分混合溶液透射光谱Fig.6 Transmission spectra of multi-component mixed solutions

2.3 IERT算法相关参数确定

2.3.1 核函数的选取

在1.1.2节核主成分分析中介绍了核函数，常用的核函数包括线性核函数、多项式核函数、高斯核函数、余弦核函数、sigmoid核函数等，实验选取上述5类作为IERT算法中的核函数，在COD，BOD5和TOC多组分混合溶液数据集上进行实验，通过结果中的决定系数值，初步选取IERT算法中的核函数。实验结果如表3所示，其中R2(ave)表示COD，BOD5和TOC的平均决定系数。

表3 IERT算法不同核函数的实验结果Table 3 Experimental results of IERT algorithm using different kernel functions

由表3可知，对于COD，BOD5和TOC这3种指标，最合适的核函数不尽相同，但sigmoid核函数的平均决定系数最大，即选择sigmoid函数作为IERT算法中的核函数，可同时满足COD，BOD5和TOC这3种指标的需求。

2.3.2 核函数的参数选择

上节中选择了sigmoid函数作为IERT算法的核函数，sigmoid函数的计算公式为式(6)所示。

k(x，y)=tanh(αxty+c)

(6)

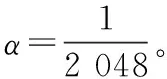
由表4可知，当sigmoid核函数在主成分数选取5和8时，均有两个指标的决定系数最大，当主成分数n选取5时，平均决定系数最大，因此选择sigmoid核函数的主成分数n为5。

表4 sigmoid核函数在选取主成分数为n时的实验结果Table 4 The experimental results of the sigmoid kernel function when the number of principal components is selected as n

表5为sigmoid核函数主成分数n为5时，在不同参数c下的决定系数。

由表5可知，当sigmoid核函数在主成分数n为5、参数c为6时，平均决定系数最大，因此IERT算法选取sigmoid核函数的主成分数n为5、参数c为6。

表5 sigmoid核函数在不同参数c下的实验结果Table 5 Experimental results of sigmoid kernel function under different parameters c

2.3.3 极端随机树中的参数选择

极端随机树中树的数量为m，表6为IERT算法在不同m下的实验结果。

由表6可知，当树的个数m取320时，平均决定系数最大，因此IERT算法选取极端随机树中树的个数m为320。

表6 IERT算法在不同参数m下的实验结果Table 6 Experimental results of IERT algorithm under different parameters m

2.4 实验结果

2.4.1 COD，BOD5和TOC多组分混合溶液实验结果

选取COD，BOD5和TOC多组分混合溶液数据集进行实验，IERT算法的核函数为sigmoid函数，主成分数n为5，参数c为6，m为320。图7为其测试集的实验结果，包括三种组分的真实值与IERT算法预测值对比和IERT算法的相对误差。由图7可以看出，在测试集中IERT算法可准确的在多组分混合溶液中预测COD，BOD5和TOC的含量。对于测试集的40个样本，其中38个样本COD的相对误差在2%以内，37个样本TOC的相对误差在2%以内，最大不超过7%； 38个样本BOD5的相对误差在10%以内。

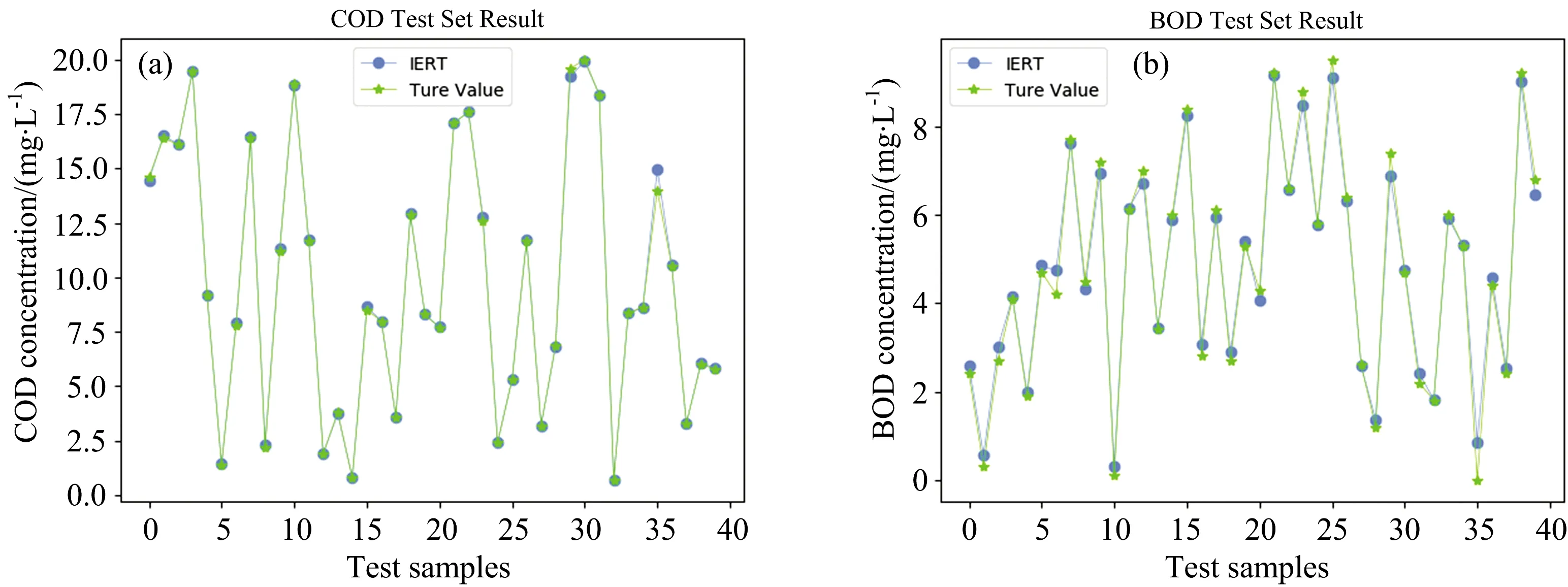
图7 IERT算法在COD，BOD5和TOC多组分混合溶液测试集实验结果(a)： COD真实值与预测值对比； (b)： BOD5真实值与预测值对比； (c)： TOC真实值与预测值对比(d)： COD预测值相对误差； (e)： BOD5预测值相对误差； (f)： TOC预测值相对误差Fig.7 Test set experimental results of IERT algorithm for COD, BOD5, TOC multi-component mixed solutions(a)： Comparison of the true value and the prediction value of COD；(b)： Comparison of the true value and the prediction value of BOD5(c)： Comparison of the true value and the prediction value of TOC；(d)： Relative error of COD prediction value； (e)： Relative error of BOD5 prediction value；(f)： Relative error of TOC prediction value

表7为IERT算法与4种对比算法的决定系数与均方根误差。

由表7可以看出，对于COD，BOD5和TOC这三种指标，IERT算法可同时预测混合溶液中的三种指标，而其他4中对比算法对多组分混合溶液中BOD5这一指标的效果均较差。同时IERT算法的决定系数均大于4种比较算法，均方根误差均小于4种比较算法。

表7 COD，BOD5和TOC多组分混合溶液中IERT算法与4种预测算法的评价参数对比Table 7 Comparison of evaluation parameters between IERT algorithm and 4 prediction algorithms for COD, BOD5, TOC multi-component mixed solutions

2.4.2 NO3-N、浊度、色度多组分混合溶液实验结果

选取NO3-N、浊度、色度多组分混合溶液数据集进行实验，由于篇幅原因，此处不在列出预测值与真实值的对比图，只列出与几种对比算法的模型评价参数对比。由表8可以看出，对于NO3-N、浊度、色度这三种指标，IERT算法也可同时预测混合溶液中的三种指标，而其他4中对比算法对多组分混合溶液中浊度这一指标的效果均较差。

表8 NO3-N、浊度、色度多组分混合溶液中IERT算法与4种预测算法的评价参数对比Table 8 Comparison of evaluation parameters between IERT algorithm and 4 prediction algorithms for NO3-N, turbidity, colority multi-component mixed solutions

2.4.3 算法计算时间实验结果

实验选择COD，BOD5和TOC多组分混合溶液数据集1和NO3-N、浊度、色度多组分混合溶液数据集2在同一硬件配置的计算机上，对5种算法所需的计算时间进行比较。实验采用的计算机硬件配置如下，处理器型号为IntelCorei7，主频为1.99 GHz，内存为16 G。表9给出了5种算法在两组数据集上所需的计算时间。

表9 IERT算法与4种预测算法的计算时间对比Table 9 Comparison of calculation time between IERT algorithm and 4 prediction algorithms

由表9可以看出，IERT算法有着不错的计算速度，与传统算法在同一量级。

3 结 论

提出了一种基于改进极端随机树的非线性全光谱定量分析算法，利用多组分混合溶液数据集进行实验，并与传统的算法进行比较，得出以下结论：

传统的光谱定量分析算法大多只适用于单组分的水质分析，在多组分混合溶液上表现较差，IERT算法通过全光谱数据进行非线性分析，相比传统的算法，具有更高的决定系数和更低的均方误差，对多组分混合溶液的预测效果很好。

IERT算法具有挖掘数据深度特征的能力，这弥补了水质在线测量中光谱定量分析算法对海浪光谱信息利用不足的劣势，使得光谱定量分析对数据的挖掘能力得到提升，有效的提升了光谱法水质在线监测的能力。

IERT算法在多组分混合溶液数据集中对浊度的检测均方根误差为0.326 4，虽为5种算法中的最优结果，但误差仍偏高，下一步工作将继续优化IERT算法对浊度的检测能力，和更多种组分混合溶液的检测能力。