TDLAS波长调制法中调制深度与高次谐波中心幅值关系的研究

陈 昊，鞠 昱，韩 立

1. 中国科学院电工研究所，北京 100190 2. 中国科学院大学，北京 100049 3. 北京航天易联科技发展有限公司，北京 100176

引 言

可调谐半导体激光光谱技术(tunable diode laser absorption spectroscopy，TDLAS)是利用气体分子对激光选频吸收，计算入射光与出射光的光功率变化，实现对待测气体浓度的定量检测。近年来大量学者对TDLAS技术进行了研究，相较于其他光谱检测技术，它具有高灵敏度、高分辨率、实时监测、便携性好、小型化等优点，在工业环保、医疗检测、气象监测等领域得到了广泛的应用[1-3]。

当气体浓度较低或气体吸收峰较弱的情况下，吸收产生的光强变化微弱，直接法(direct absorption spectroscopy，DAS)测量无法获得理想的信噪比，需要采用谐波法(wavelength modulation spectroscopy，WMS)进行检测，它是利用锁相放大器解调特定频率的谐波进行检测，计算各次谐波峰值或者峰值比表征气体浓度，具有更低的检测下限和灵敏度[4-5]。各次谐波信号与调制深度m相关，当m≈2.2时，二次谐波的峰值达到最大； 当m≈4.1时，四次谐波的峰值达到最大[6]。当气压发生剧烈变化时，气体半高宽随气压变化[7]，而调制深度为调制频率幅度与气体半高宽的比值，因此调制深度也受气压影响，导致各次谐波的幅值和信噪比都受到影响，测量结果容易产生误差。

如何确定当前气压环境下的调制深度值就显得至关重要，基于此本文研究了TDLAS技术中谐波法的原理，推导了在中心频率位置下的一次谐波、二次谐波、三次谐波以及四次谐波幅值强度表达式，四次谐波与二次谐波中心幅值强度比只与调制深度值相关，建立了调制深度函数，通过调制深度函数来推算当前环境下的调制深度值，再调整调制频率幅度，使调制深度m尽可能接近2.2，来保证二次谐波信号的幅值保持在最大值，提高信噪比和测量精度。

1 TDLAS调制深度函数

TDLAS技术理论基础是Beer-Lambert定律，它描述了一束特定频率的激光进入气体样品前后的光强变化，如式(1)所示。

It=I0exp[-α(ν)cL]

(1)

式(1)中，It为穿过待测气体后的透射光光强，I0为入射光强，α(ν)为吸收系数，c为待测气体的浓度，L为光吸收路径长度。

对于谐波法，光源的驱动电流叠加了一个低频的小信号，激光器的出光频率和光强都会产生调制。

(2)

(3)

(4)

当采用洛伦兹线型表示吸收系数α(ν)时

(5)

式(5)中，ν0为气体吸收峰中心频率，S为气体吸收线强，N为标准状况下(STP)的气体摩尔分子数，γ为待测气体吸收谱半高宽，f(ν)为洛伦兹线型函数，调制深度m=a/γ，令a0=SN/πγ，即气体吸收峰中心位置(ν=ν0)的吸收系数，则式(5)简化为

(6)

对于气体吸收峰中心位置，即ν=ν0，式(6)代入式(4)得

(7)

对式(7)按照ω进行傅里叶级数展开，得到气体吸收峰中心位置的各次谐波强度，其中一次谐波到四次谐波幅值强度表达式如式(8)—式(11)

(8)

(9)

(10)

(11)

利用四次谐波式(11)与二次谐波式(9)幅值强度进行比值计算，得到一个关于调制深度m的表达式。

(12)

中心频率位置下的四次谐波与二次谐波比值仅与调制深度m相关，与浓度、温度、入射光强都不相关，根据式(12)可以得到当前气压环境下的调制深度值m。待测气体浓度的表征方式是以二次谐波峰值(即吸收峰中心位置，ν=ν0)与标准浓度值进行拟合表示，根据式(9)可知，当m≈2.2时，二次谐波幅值强度达到最大，信噪比最好，通过计算四次谐波与二次谐波的比值得到当前气压环境下的调制深度m，调整调制频率幅度a，让调制深度m尽可能接近2.2，以此获得幅值最强、信噪比最好的二次谐波信号，提高测量准确度。

2 仿真分析

2.1 调制深度函数曲线

根据式(9)、式(11)以及式(12)可以得到在中心频率处的，二次谐波中心幅值I2f(m)、四次谐波中心幅值I4f(m)以及两者幅值强度比值I4f/I2f(调制深度函数f(m))关于调制深度m的函数曲线，如图1所示。

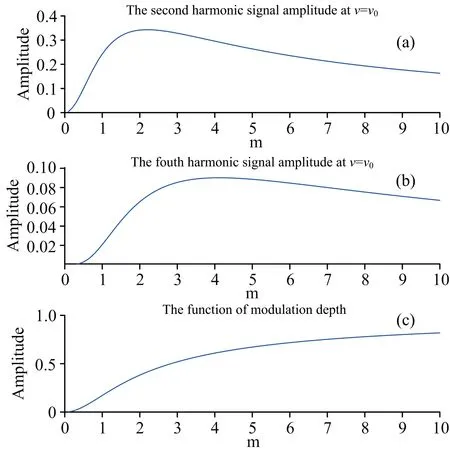
图1 二次谐波中心幅值、四次谐波中心幅值以及调制深度函数曲线Fig.1 Second harmonic center amplitude, fourth harmonic center amplitude and modulation depth function curve

图1(a)是二次谐波幅值I2f随调制深度m变化的曲线，I2f(m)不是单调的，当m≈2.2时，二次谐波幅值达到最大值； 图1(b)是四次谐波幅值I4f随调制深度m变化的曲线，I4f(m)也不是单调的，当m≈4.1时，四次谐波幅值达到最大值； 图1(c)是调制深度函数曲线f(m)，它是单调递增的函数。实测中为了获得更好的二次谐波信噪比，应该尽可能将调制深度控制在2.2附近，而I2f(m)与I4f(m)都是非单调的，存在一个最大值，通过I2f(m)与I4f(m)的曲线变化来判断当前调制深度就显得尤为困难，但是调制深度函数f(m)是单调递增，并且只与调制深度m相关，因此根据调制深度函数f(m)，计算四次谐波与二次谐波幅值强度比值来反推当前环境下的调制深度是可行的，并具有唯一性。

2.2 仿真验证

为了验证调制深度函数f(m)反推调制深度的可行性，选择水汽中心频率为7 306.752 1 cm-1作为吸收峰，吸收强度为1.8×10-20cm-1·(molec·cm-2)-1，气体浓度设定为1 000 ppm，吸收光程为30 cm，模拟了气压从0.3～1.5 atm时二次谐波以及四次谐波信号，并对其进行了分析。

图2(a)是气压0.3～1.5 atm时的二次谐波模拟信号，二次谐波中心幅值在p=0.9 atm时达到最大，此时调制深度理论值为2.378 8，二次谐波中心幅值最大值位置与图1中I2f(m)曲线结果相吻合； 图2(b)是气压0.3～1.5 atm时的四次谐波模拟信号，四次谐波中心幅值在p=0.5 atm时达到最大，此时调制深度理论值为4.281 9，四次谐波中心幅值最大值位置与图1中I4f(m)曲线结果相吻合。表1计算了各个气压下的调制深度m和四次谐波与二次谐波中心幅值比I4f/I2f的理论值和仿真值，随着气压的升高，调制深度理论值逐渐减小，四次谐波与二次谐波中心幅值比的理论值和仿真值最大相对误差为-1.44%，反推的调制深度的理论值与仿真值最大相对误差为1.78%，说明了仿真下的实际调制深度函数f(m)与理论函数式(12)接近，符合理论推导。

表1 不同气压下调制深度和四次谐波二次谐波中心幅值比的理论值和实际值Table 1 Theoretical and practical values of modulation depth m and harmonic center amplitude ratio under different air pressure

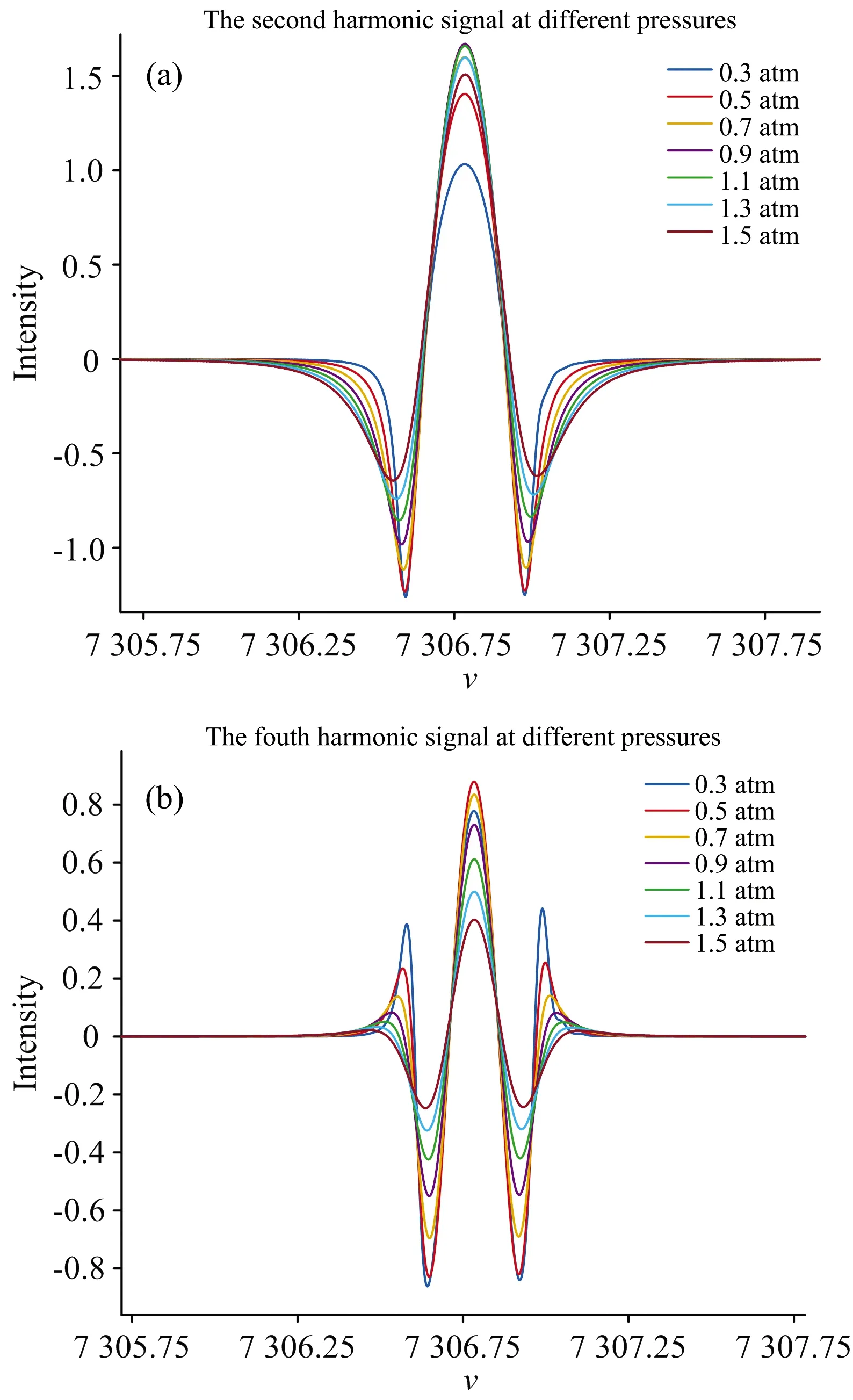
图2 不同气压下二次谐波与四次谐波的仿真信号Fig.2 Simulation signals of the second and fourth harmonics under different air pressures

3 实验部分

仿真结果验证了调制深度函数f(m)的仿真结果与理论值一致，下面进一步用实验进行论证。实验装置示意图如图3所示，TDLAS水汽测试系统选用中心频率为7 306.79 cm-1的DFB半导体激光器作为光源，气室探头的吸收光程为30 cm，采用锁相放大的方式对二次谐波和四次谐波信号进行提取。国瑞智GRZ5013湿度发生器产生低浓度水汽气体，浓度设定为1 000 ppm，自制密封箱内放入气室探头并接入压力传感器，做好密封处理，实验前将密封箱内气体抽空，随后将1 000 ppm的水汽气体通过气体阀门缓慢通入密封箱内，通过控制阀门来调节密封箱内的气压，记录不同气压条件下的二次谐波与四次谐波信号。

图3 实验装置示意图Fig.3 Schematic diagram of experimental device

4 结果与讨论

根据所搭建的实验装置，通过国瑞智GRZ5031湿度发生器浓度产生1 000 ppm的水汽，调节减压阀门控制密封箱的气压范围在10.4～177.9 kPa，相敏检波器输入二倍频和四倍频的参考信号，调整滤波器和放大器参数，得到了不同气压下的二次谐波和四次谐波信号，如图4所示。

图4 不同气压下的二次谐波和四次谐波实测信号Fig.4 Measured second and fourth harmonic signals at different air pressures

图4(a)是不同气压下的二次谐波信号，图4(b)是不同气压下的四次谐波信号，计算了中心频率下的二次谐波和四次谐波信号的幅值以及幅值比I4f/I2f，利用式(12)调制深度函数f(m)推算了各个气压下的调制深度值，如表2所示。

根据表2中的中心频率下的幅值比以及对应的调制深度m值，可以得到二次谐波I2f(m)和四次谐波I4f(m)曲线，如图5所示。当m=2.226 7时，实测的二次谐波中心频率幅值达到最大值，而m=4.061 0时，实测的四次谐波中心频率幅值达到最大值，这与图1理论结果的m≈2.2时二次谐波幅值达到最大值以及m≈4.1时四次谐波幅值达到最大值有很好的吻合。图5中实测的二次谐波I2f(m)和四次谐波I4f(m)的函数曲线与图1的理论曲线变化趋势相同，说明了通过调制深度函数f(m)推算的调制深度值m接近实际环境下的调制深度值，并未存在较大误差，论证了理论的准确性。

表2 不同气压下的二次谐波与四次谐波的中心幅值、幅值比以及调制深度Table 2 Central amplitude, amplitude ratio and modulation depth m of the second and fourth harmonics under different air pressures

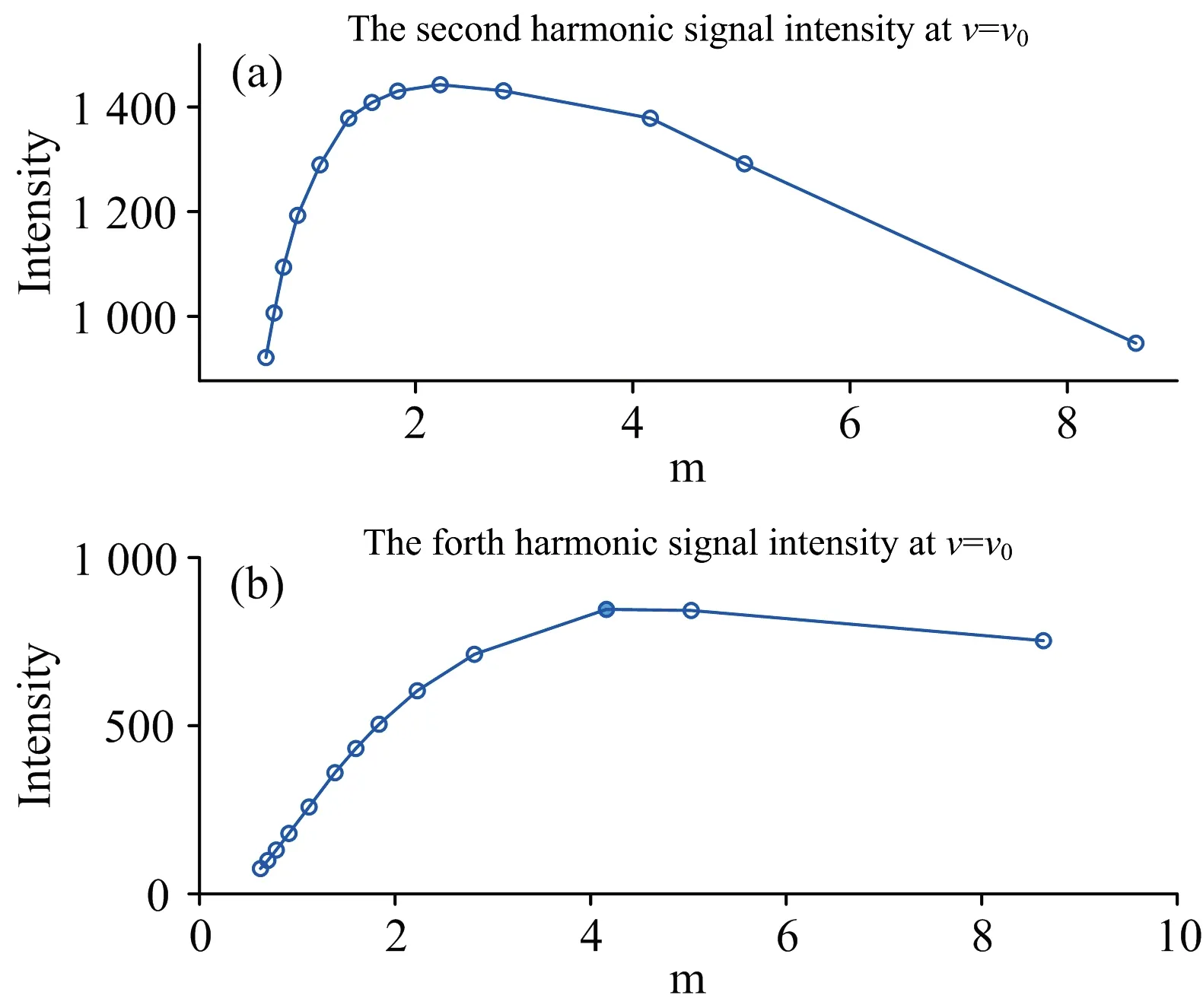
图5 实测的二次谐波和四次谐波中心幅值曲线Fig.5 Curves of measured second harmonic and fourth harmonic center amplitude

为了进一步验证理论的准确性，计算调制深度m与气压p的乘积值可以来判断结果的准确性，气体半高宽γ表达式如式(13)所示

(13)

式(13)中，n为温度系数，p0和T0分别为标准气压和标准温度，γair是空气吸收谱线半高宽，γself是待测气体吸收谱线半高宽。根据式(13)可知气体半高宽γ在温度和气体浓度不变的情况下与气压p是正相关的，即γ=εp，ε为正相关系数，而调制深度m=a/γ，调制频率幅度a=mγ=εmp。实验中湿度发生器产生固定浓度为1 000 ppm的水汽并且保持密封箱内温度恒定，因此实测的调制深度m与气压p的乘积应该为定值，即mp=a/ε，因此计算不同气压下mp值可以验证推算的调制深度是否准确。图6为不同气压条件下关于mp平均值的相对误差曲线。

图6 不同气压条件下关于mp平均值的相对误差曲线Fig.6 Relative error curve of mean value of mp under different pressure conditions

根据图6所示，mp的平均值为109.46，各个气压条件下的mp值的相对误差显示，在10.4 kPa

5 结 论

TDLAS波长调制法中谐波信号受气压影响较大，经研究发现气压的影响是调制深度对谐波信号的影响，本文研究了各次谐波与调制深度的关系，通过计算四次谐波与二次谐波中心幅值比，利用调制深度函数推算当前气压环境的调制深度，调整调制频率幅度，使得调制深度接近各次谐波最佳调制深度值，谐波信号信噪比最佳，为验证结论进行了仿真与实验。仿真结果显示： 四次谐波与二次谐波中心幅值比的理论值和仿真值的最大相对误差为-1.44%，调制深度理论值与仿真值的最大相对误差为1.78%，说明了仿真下的调制深度函数曲线与理论函数式(12)接近，符合理论推导。实验结果显示： 根据调制深度函数推算的调制深度值，当m=2.226 7时，实测的二次谐波中心频率幅值达到最大值，而m=4.061 0时，实测的四次谐波中心频率幅值达到最大值，与仿真结果一致； 在30.2 kPa