基于PSO-NM 两步识别法的桥梁损伤识别与数值仿真

赵 展，张 鹏，乔升访

（1、广州建设工程质量安全检测中心有限公司 广州 510440；2、广州市建筑科学研究院集团有限公司 广州 510440；3、广州建筑股份有限公司 广州 510030）

0 前言

结构损伤识别（SDD）是结构健康监测的一个重要分支［1-2］，怎么将结构损伤识别成果应用于结构健康监测上已成为近些年的主要研究趋势［3-6］。其中，将SDD问题转化为数学优化问题，然后采用优化算法求解，是结构损伤识别研究的一个重要方向［7］。对于求解SDD 问题，已有学者提出了许多优化算法［8-10］，其中粒子群优化算法（PSO）是最常用的算法之一。

粒子群优化算法是一种基于种群的自适应搜索技术，由KENNEDY 和EBERHART 于1995 年提出。近年来，粒子群优化算法在土木工程问题中得到了广泛应用，并取得了良好的效果。但如何提高计算效率，避免识别结果陷入局部最优仍然是一个难题。许多学者致力于在计算效率和准确性之间找到平衡。BAGHMISHEH 等 人［11］提 出 了 一 种 结 合PSO 和Nelder-Mead（NM）算法的混合PSO-NM 算法。对悬臂梁的实验结果表明，该方法能够以较小的误差检测结构微小裂纹。SEYEDPOOR［12］提出了一种两步方法，即使用基于模态应变能的指数（MSEBI）定位损伤，并根据MSEBI 的结果应用粒子群算法确定实际损伤程度，通过悬臂梁和桁架的数值模拟结果表明其方法可以准确识别结构多重损伤。

在本研究中，将粒子群优化算法与NM 算法相结合，提出了一种新的用于结构损伤的两步识别法，以探索计算效率和精度之间的平衡。选用桥梁结构作为数值仿真实例，以用来评估此识别方法的适用性。

1 改进的混合PSO-NM 算法

1.1 目标函数

结构损伤识别包含静力识别和动力识别方法。模态数据是动力识别法常用的数据类型。当结构发生损伤时，其模态数据会发生相应改变，此时可以通过最小化试验模态数据与相应的计算结果来估计结构损伤。当实验结果与计算结果的误差最小时，对应的数值模型参数可作为结构状态评估的量化值。

通常优化问题可以定义为以下形式：

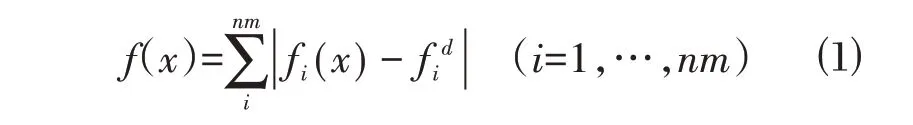
式中：f为频率；nm为使用的振型数；i为第i个振型；d表示损伤状态。

1.2 结构损伤定位

一般来说，结构损伤可仅考虑单元刚度的折减。当损伤发生时，通过降低弹性模量来进行模拟。损伤单元刚度的降低会导致单元节点位移的增加。因此，当损伤模态形状与健康模态形状比较时，损伤单元处存在一个峰值。通过搜索这些峰值可以定位损伤。

根据结构动力学理论，结构振动的特征方程为

由于损伤单元刚度未知，因此近似取未损伤单元刚度进行计算。结构损伤会导致损伤单元的MSEBI值增加。因此，如果式⑸的值大于0，则可以判定该单元发生损伤。

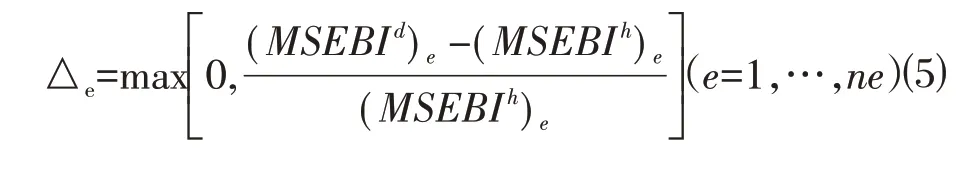
1.3 结构损伤量化

PSO-NM 是一种混合智能算法。该算法在每次迭代时使用NM 对PSO 的结果进行优化，以避免算法陷入局部最优。

PSO 是一种基于种群的自适应搜索技术。优化问题的可能解可以看作是多维空间中的一个点，称为“粒子”。如图1 所示，PSO 从搜索空间中的随机粒子群开始，通过调整每个粒子朝向其自身最佳位置和整个群的最佳粒子的轨迹来找到全局最优解。

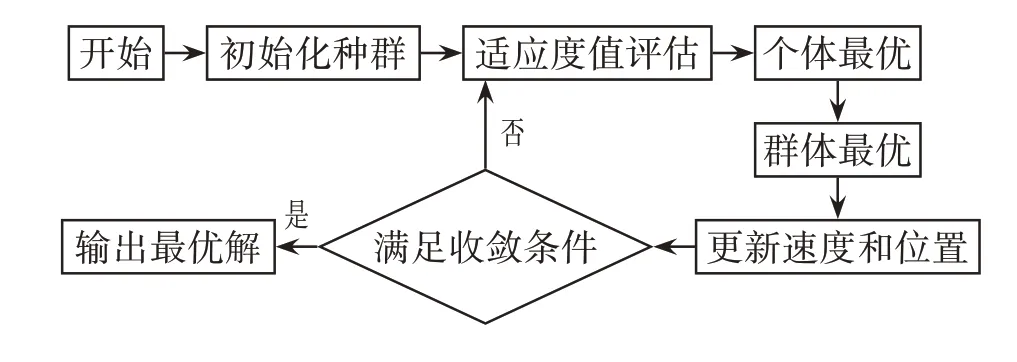
图1 粒子群算法Fig.1 Particle Swarm Optimization

NELDER 和MEAD 在1965年引入的NM 单纯形算法是一种多维无约束极小值优化方法［11］。对于n维优化问题，NM 方法首先围绕当前解建立初始单纯形，然后根据其适应值对单纯形的n+1 点进行排序。NM 方法的主要思想是用另一个适应度值更小的点替换单纯形的最坏点（具有最大适应度值），主要通过反射、膨胀、收缩和收缩4种变换实现，如图2所示。通过这个操作，可以使单纯形向最佳点收缩，得到问题的最优解。

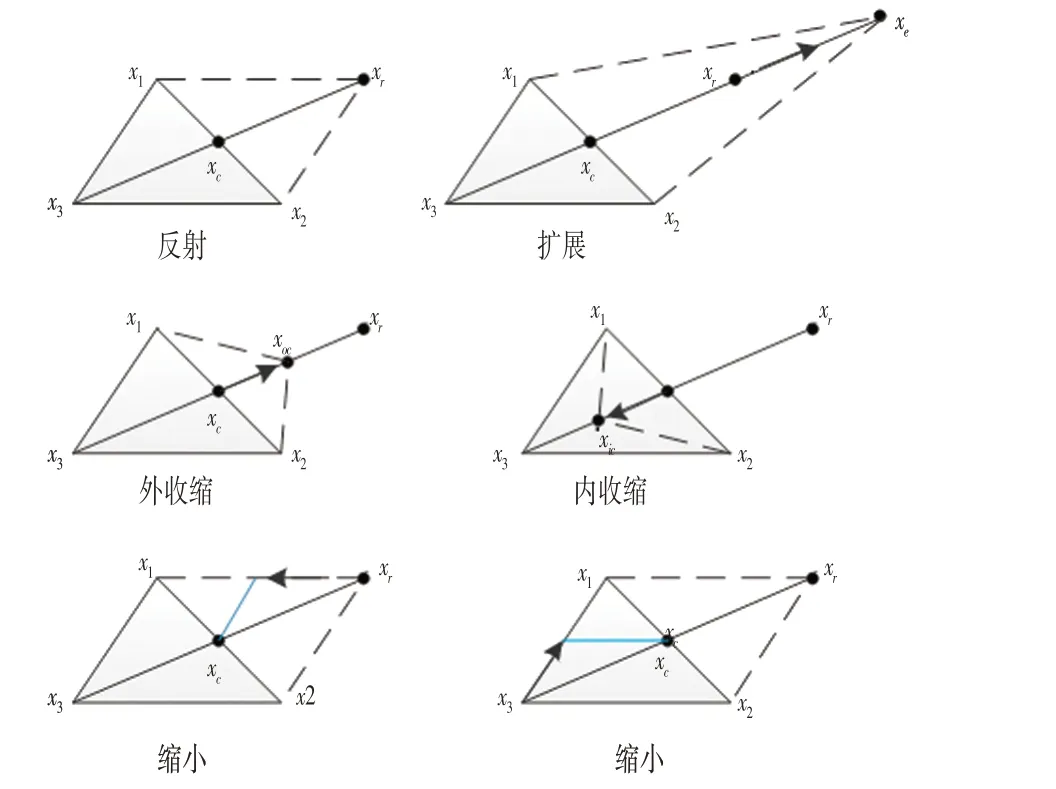
图2 NM算法Fig.2 Nelder-Mead Algorithm

2 数值模拟

2.1 简支梁

为了验证所提出的方法，考虑了具有10个单元的简支梁式桥梁，如图3所示。桥梁长度为1.0 m，截面为0.1 m×0.1 m，弹性模量为70 GPa，密度为2 700 kg/m3。

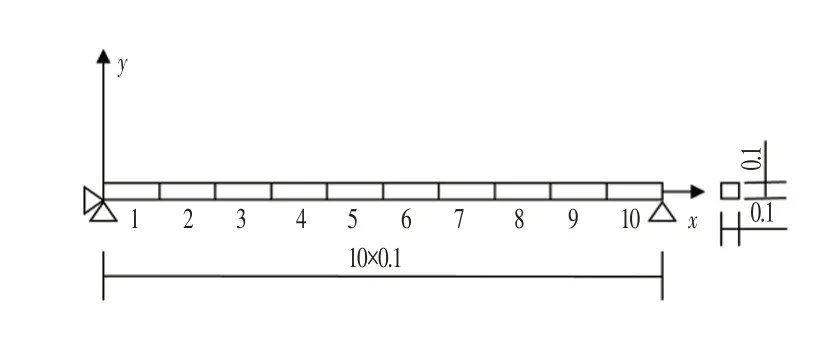
图3 简支梁式桥梁Fig.3 Simply Supported Beam Bridge （m）

本文考虑了一些损伤情况，包括单损伤和多损伤。损伤单元的选择取决于最可能的损伤区域，即跨中处的最大挠度位置以及靠近支座端的做大剪应力处。10单元梁的损伤情况如表1所示。

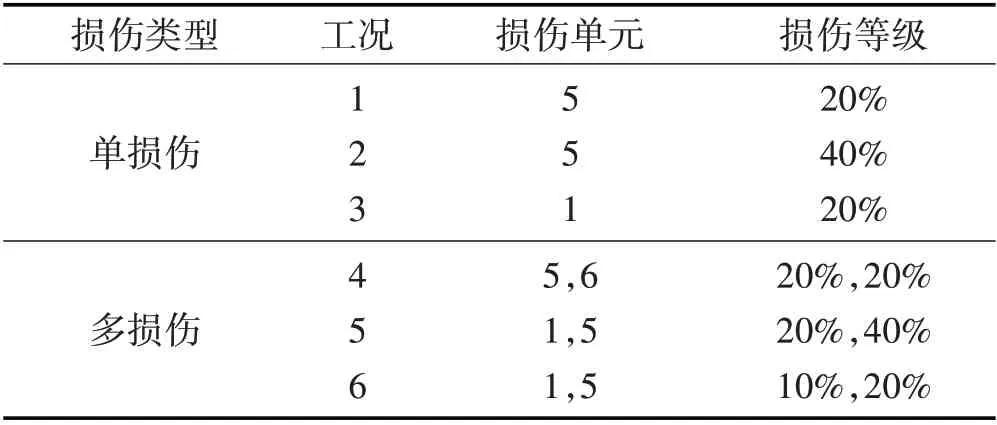
表1 损伤情况Tab.1 The Extent of the Damage

结构损伤识别问题的目标函数可以表示为式⑹，其中x是范围［0，1］内的损伤程度向量。x=0 表示单元无损伤，x=1 表示元件完全损伤。无损伤结构和损伤结构振型之间的最小值定义为：

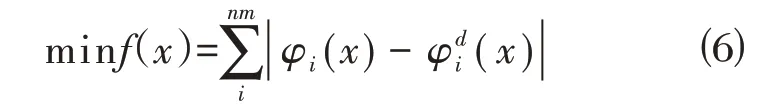
其中x∈［0，1］（i=1，…，nm）

在第一步识别中，根据式⑸计算MSEBI 值。表2所列6 种工况下的MSEBI计算结果如图4 所示。如式⑸所定义，如果MSEBI的值大于0，则相应的单元可视为损伤单元。因此，可以看出，图4 中的定位结果与真实损伤位置基本一致。MSEBI损伤定位值表明了损伤单元的定位是准确的。此外，它适用于具有不同损伤程度的单损伤情况和多损伤情况。

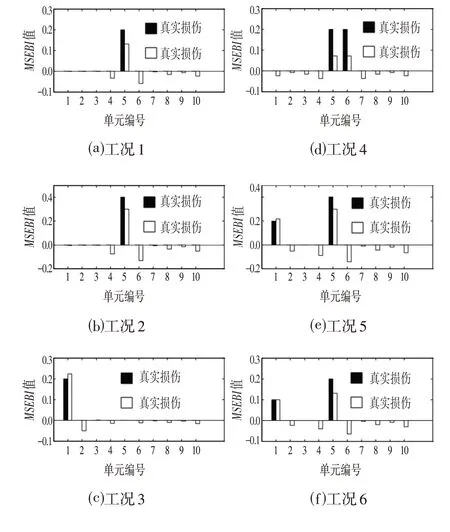
图4 MSEBI 损伤定位结果Fig.4 Results of Damage Localization in MSEBI

在第二步识别中，每次计算的迭代次数设置为20，粒子群设置为20，对同种工况分别进行10 次计算，以避免单次识别误差过大的情况。10次计算的最终结构损伤识别结果如图5所示。“E1”表示1号单元。通过比较不同情况下的结果，可以发现所提出的新型两步识别法可以识别单个或多个损伤情况下的损伤位置和损伤程度。工况1 和工况2 的结果也表明，该方法适用于不同程度的损坏。工况1和工况3的结果说明了其在不同损伤元素识别中的应用。对于多个损坏情况也可以得出相同的结论。

图5 损伤量化结果Fig.5 Damage Quantification

2.2 连续梁

此外，考虑两跨连续梁进行损伤识别，如图6 所示。材料特性与表1 中的相同。连续梁分为20 个单元。并考虑了2 种损伤情况，包括单元5 发生的单一损伤和单元5 和单元15 发生的2 种损伤。单一损伤工况为40%@5，而2种损伤工况为30%@5和40%@15。

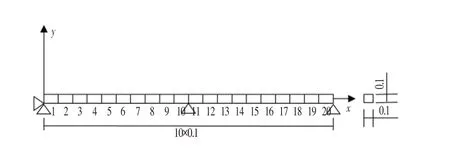
图6 连续梁模型Fig.6 Continuous Beam Model （m）

本文提出的两步识别法用于连续梁模型的结构损伤识别，在单个和多个损伤情况下，损伤定位结果如图7所示，损伤量化结果如图8所示。可以看出，所提出的两步识别法也适用于连续梁结构的结构损伤识别。

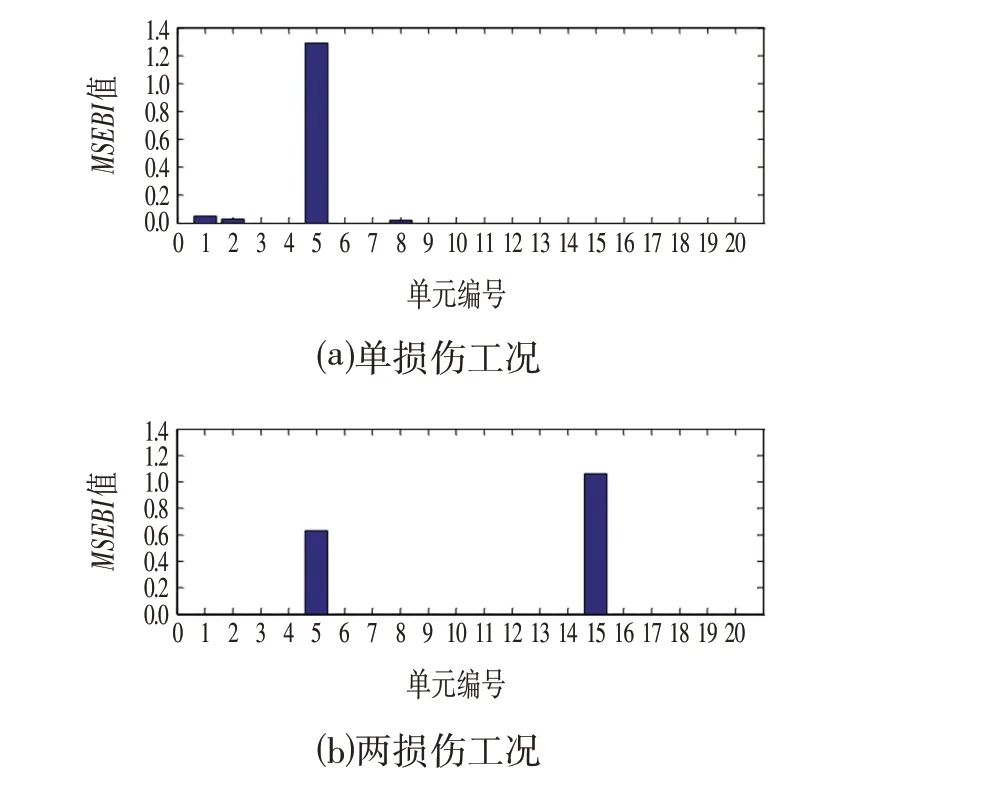
图7 MSEBI 损伤定位结果Fig.7 Results of Damage Localization in MSEBI

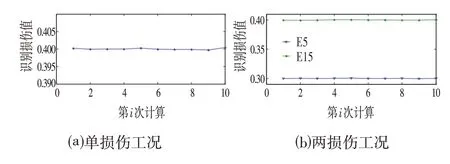
图8 损伤量化结果Fig.8 Damage Quantification

3 结论

本研究将粒子群优化算法与NM 算法相结合，提出了一种用于梁式结构损伤识别的两步识别法，以用于探索计算效率和精度之间的更好平衡。具体采用一些梁式结构的例子来评估这种新型智能方法的适用性。得出以下结论：

⑴ 本文所提出的两步PSO-NM 智能算法适用于梁式结构的结构损伤识别，如简支梁和连续梁。它可以提供单损伤和多损伤工况的精确识别结果，同时多步法的引进有效提高了计算的效率。

⑵ 本文提出的两步PSO-NM 智能算法不仅可以基于MSEBI 值对结构进行损伤定位，而且可以很好地量化结构损伤程度。

⑶ 在本研究中，一些数值模拟表明，所提出的两步PSO-NM 智能算法已成功应用于梁式结构的结构损伤识别，但仍需通过未来大规模实际结构的实验数据进行验证。