±535 kV直流断路器用隔离供能变压器电场计算与起晕校核

岳国华，杜志叶，李根，修连成，易凡

(1.武汉大学电气与自动化学院，武汉430072；2.空军预警学院雷达士官学校，武汉430345)

0 引言

为了实现碳达峰、碳中和的“双碳”目标，新能源的大规模接入离不开以直流输电技术为核心的新型电力系统[1-3]。与交流系统相比，直流系统的故障控制难度更大，为了保证直流输配电网的安全运行和设备正常工作，配置直流断路器成为了最为有效的技术手段之一[4-5]。直流断路器供能用隔离变压器(以下简称：供能变压器)作为直流断路器获取能量的核心设备，保证其正常运行是直流断路器正常开断故障电流的保障[6-7]。如果供能用隔离变压器结构设计不当，就会产生电晕放电与绝缘闪络问题[8]，导致换流站阀厅周围的无线电干扰水平超标，可听噪声明显，产生严重的电磁环境污染，影响人员安全[9-10]。针对此问题，研究人员通常采用电场校核的方法进行结构设计与优化[11-12]，使设备各部分表面的最大电场强度小于控制场强。

1 计算方法简介

在采用有限元法进行电场计算时，根据所求解电场性质的不同，可以将其分为瞬态电场与静态电场，其中静态电场又可以细分为静电场与恒定电场。当供能变压器正常工作时，其整体稳态工作电压为直流535 kV，子隔离变压器单元工作电压为交流350 V。理论上，这样交直流混合的复杂情况在计算电场时需要采用瞬态场的方法求解。为了保证计算结果的精确度，在瞬态场求解时，需要划定较短的时间步长，而对求解器来讲，每一步都需要对整个模型重新进行完整的计算，计算量大且耗时长，尤其对于求解供能变压器这种复杂的模型，即便采用高性能的计算设备也很难完成。工程上在处理此类问题时常采用静态电场进行代替[13]，一定程度上可以大为减少所需要的计算量，但是静态电场类型选取的不恰当，会引入一定的误差，对后续的深入分析产生不利影响[14-15]。

1.1 电场计算的基本方程

静电场与恒定电场同属于静态电场，所谓静态电场指的就是由电荷激发的，不随时间改变的电场，这是和瞬态电场(电场随时间变化)的主要区别。

静电场是由静止电荷激发的，其控制方程为：

(1)

式中：ε为介电常数；φ为标量电位；ρ为自由电荷体密度。可以看出，静电场存在于电介质空间中，其电位的分布与电介质的介电常数ε相关。

恒定电场的控制方程为：

(2)

式中γ为电导率。可以看出，恒定电场存在于导电媒质空间中，其电位的分布与导电媒质电导率γ相关。

瞬态电场的控制方程可由麦克斯韦方程组得出。在工频下，电气设备内部的电场与磁场耦合关系极弱，因此可以忽略磁场变化(∂B/∂t)对电场的影响，其控制方程为：

(3)

(4)

式中E为电场强度。瞬态电场中电位的分布与介电常数ε和电导率γ这两者均相关。当式(3)中γ为0，即不考虑电导率时，由式(3)可推导出式(1)；当式(3)中ε为0，即不考虑介电常数时，由式(3)可推导出式(2)。因此不论是静电场还是恒定电场，他们都是瞬态电场的特殊形式。

当场中的自由电荷体密度ρ为0时，式(1)与式(2)均可简化为：

(5)

由于两种场的控制方程完全一致，若这两种场的边界形状与赋值也完全相同，那么在均匀介质中，静电场与恒定电场的计算结果也应相同。

当整个求解场域中有多种介质时，在单一的介质中，式(5)仍然满足，但是静电场与恒定电场在介质分界面上边界条件不再相同，因此对应的场分布也会不同。在无自由电荷分布区域的静电场中，两个不同介质交界面的边界条件为：

E1t=E2t

(6)

ε1E1n=ε2E2n

(7)

式中：下标t表示切向分量；下标n表示法向分量；下标1、2表示两种不同介质。E1tE2tE1nE2n分别为电场强度在1、2介质中切向和法向的电场强度。ε1、ε2分别为1、2介质的介电常数。

在恒定电场中，两个不同介质交界面的边界条件为：

E1t=E2t

(8)

γ1E1n=γ2E2n

(9)

对比式(7)和式(9)可得，对于有n种介质存在的稳态电场求解问题，只有当介质的材料参数满足式(10)时，静电场与恒定电场的计算结果才会相同，因此在对设备进行电场校核时，需要考虑上述两种电场计算结果的差异。

(10)

1.2 空气电导率对恒定电场的影响

在电场的有限元仿真中，模型的材料类型主要分为3种，分别为：导体、绝缘、空气，其中导体与绝缘的参数一般是确定的，与设备实际采用的材料有关，而作为求解域的空气参数则需要根据电场的类型而确定。在静电场中，空气的相对介电常数一般设为1[15]，但是在恒定电场中，由于空气电导率经常受温度、湿度、离子浓度等因素影响[16-19]，不同文献对空气电导率的取值都有所不同。根据文献[20]，在空气温度低于5 000 K时，空气电导率几乎不随温度发生变化。根据文献[21]，大量观测结果表明，全球地表面大气总电导率平均 值为2.3×10-14S/m，变化范围在2×10-15S/m到0.6×10-13S/m之间。根据文献[22]，在70%空气湿度下，空气电导率约为0.9×10-14S/m，且随着空气湿度的增加或减小，电导率会随之增加或减小，变化范围在1个数量级左右。综上所述，可以认为空气电导率容易收到湿度的影响，最大的变化范围处在10-16～10-12S/m之间。考虑到恒定电场的边界条件，空气电导率在此范围内的变化势必会对隔离变压器绝缘材料表面电场的计算结果产生影响，因此要研究恒定电场，就需要按照不同的空气电导率进行讨论分析。

在电气设备中，导体材料主要为铝、铜、铁，以及这些材料组成的合金，电导率的数量级为107S/m；绝缘材料主要为硅橡胶、环氧树脂、XLPE等，电导率的数量级为10-14S/m；空气的电导率数量级在10-16～10-12S/m之间波动。可以看到，绝缘材料与空气的电导率在数量级上非常接近，而与导体相差较大，根据恒定电场中的折射定律：

(11)

在导体-空气交界面上，下标1表示导体材料，2表示空气，由于γ1远远大于γ2，即使γ2在几个数量级内变化，空气侧电场强度的方向也不会发生明显变化，近似与导体表面保持垂直，因此电场强度的值也不容易发生变化。在绝缘-空气交界面上，1表示绝缘材料，2表示空气，由于两者电导率相近，当γ2发生变化时，空气侧电场强度的方向会发生明显变化，同时电场强度的值也会随之发生变化。

在实际的供能变压器中，绝缘材料主要用在变压器的套管与支柱绝缘子上，为了提高闪络电压，这些绝缘材料都被设计成多个伞裙结构，一个典型的单个简化伞裙轴对称模型如图1所示。其中导体电导率设置为107S/m，绝缘电导率为10-14S/m。令空气电导率在10-16～10-12S/m范围内变化，计算模型伞裙端部的电场强度，结果如图2所示。

图1 典型的单个简化伞裙轴对称模型

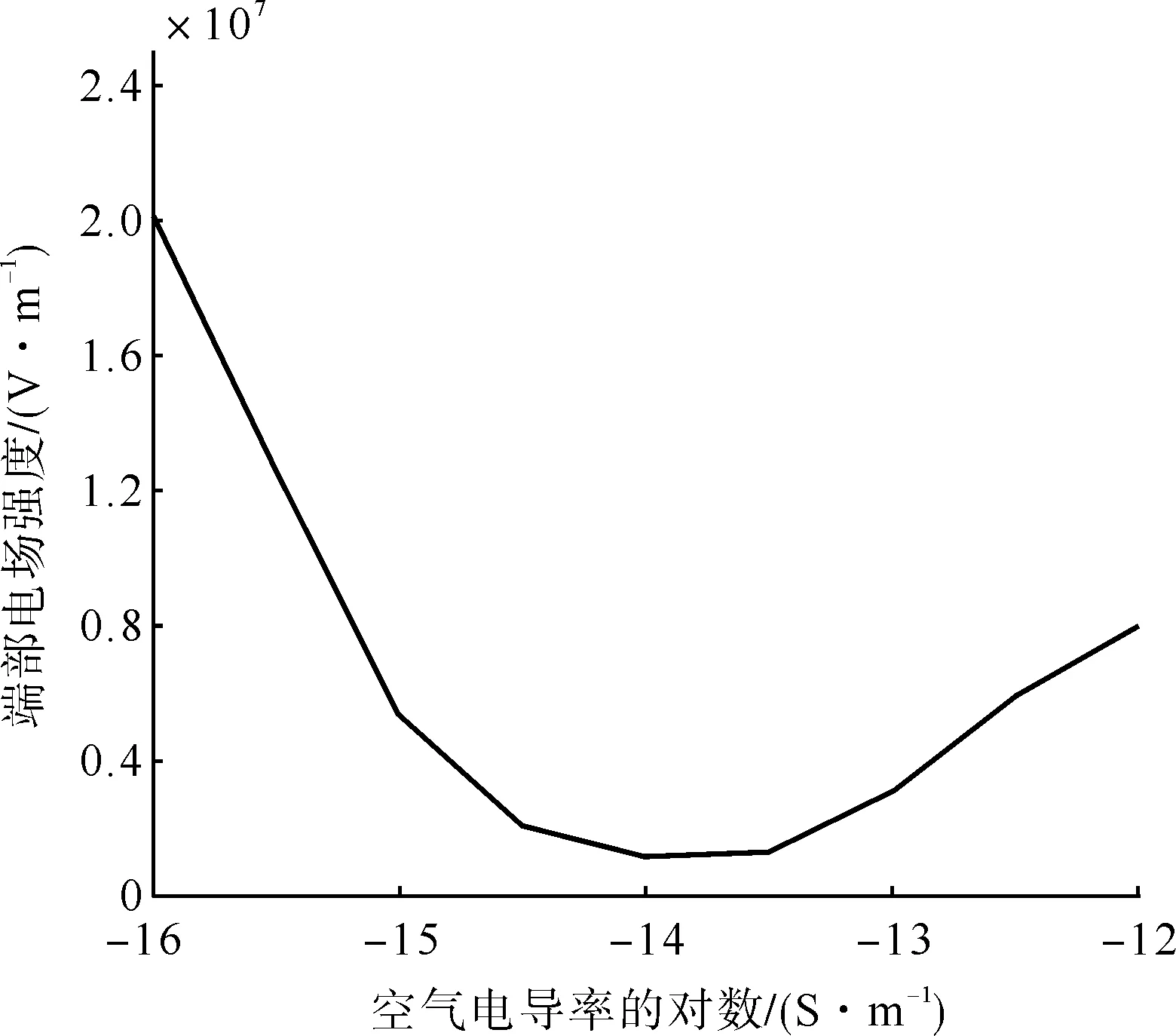
图2 端部场强随空气电导率变化图

可以看到，绝缘材料伞裙结构端部的电场强度随着空气电导率的增大先减小后增大，在空气电导率和绝缘材料电导率接近时，其值较小，这与伞裙边缘尖角结构导致电场方向发生突变有关。方向的突变引起了电场强度值的畸变，当空气电导率与绝缘材料电导率相差较大时，畸变严重，因而电场强度比较大；而当空气电导率与绝缘材料电导率接近时，整个场近似均匀介质，特殊尖角结构对电场影响较小，此时电场不再畸变，因而电场强度也较小。由于不同空气电导率下的最大电场强度差达到了10倍以上，如果在电场校核时选择了不恰当的空气电导率，势必会对设备后续的安全产生影响。

1.3 电场校核的原则

基于上述分析，考虑到空气电导率的影响，在对类似供能变压器的交直流混合设备进行电磁环境的电场计算时，其流程图如图3所示。

图3 交直流混合电场校核的流程图

2 供能变压器有限元模型构建

2.1 模型介绍

本文以±535 kV直流断路器用隔离供能变压器作为研究对象，对其进行了三维建模。建模过程考虑了屏蔽罩、阻容分压屏蔽环、顶层屏蔽环、子变压器及其内部结构、各层夹件、支柱绝缘子及各连接金具。建模时对供能变压器的5层结构进行了不同的处理，通过合理推论及简单计算验证，可以得出高场强区域主要出现在最上层，所以对最上层结构进行了较为精细的建模，保留了支柱绝缘子的伞裙结构，以便于分析该处沿面电场分布特征。而对于下面电位较低的各层则进行了必要的简化，简化方式对整体模型以及关注区域电场强度的计算精度影响不大。供能变压器的三维有限元模型如图4所示。

图4 供能变压器有限元模型图

为了保证足够的求解精度，对隔离变压器模型外加空气包来确定求解域，其中内空气包为4 m×4 m×8.5 m，根据设备安装室内环境，外空气包设为20 m×20 m×25 m。

2.2 参数设置

供能变压器外绝缘主要采用硅橡胶作为绝缘材料，包括各支柱绝缘子和变压器套管。各连接金具、均压金具设置为导体，包括各均压环、屏蔽罩、夹件、铁心、连接件等结构。仿真时采用的材料参数均来自实际的设计值，主要的材料设置如表1所示。

表1 材料参数设置

本文介绍的535 kV隔离供能变压器是由10个变比为1:1的子隔离变压器级联而成，这些子隔离变压器被分成5层，每层2个，正常工作时传输的工频交流电压有效值为350 V，最大值约为500 V，直流母线上的电压为535 kV，叠加后的最大电压为535.5 kV。如图5所示，根据供能变压器的电路原理图确定电位加载，不考虑部分电容的影响，认为10个阻容分压器把最大电压均匀的分成11个部分，其中顶层V1电压最高为535.5 kV，底层V11电压最低为0 V，空气域的外表面以及大地的电位设为0电位。

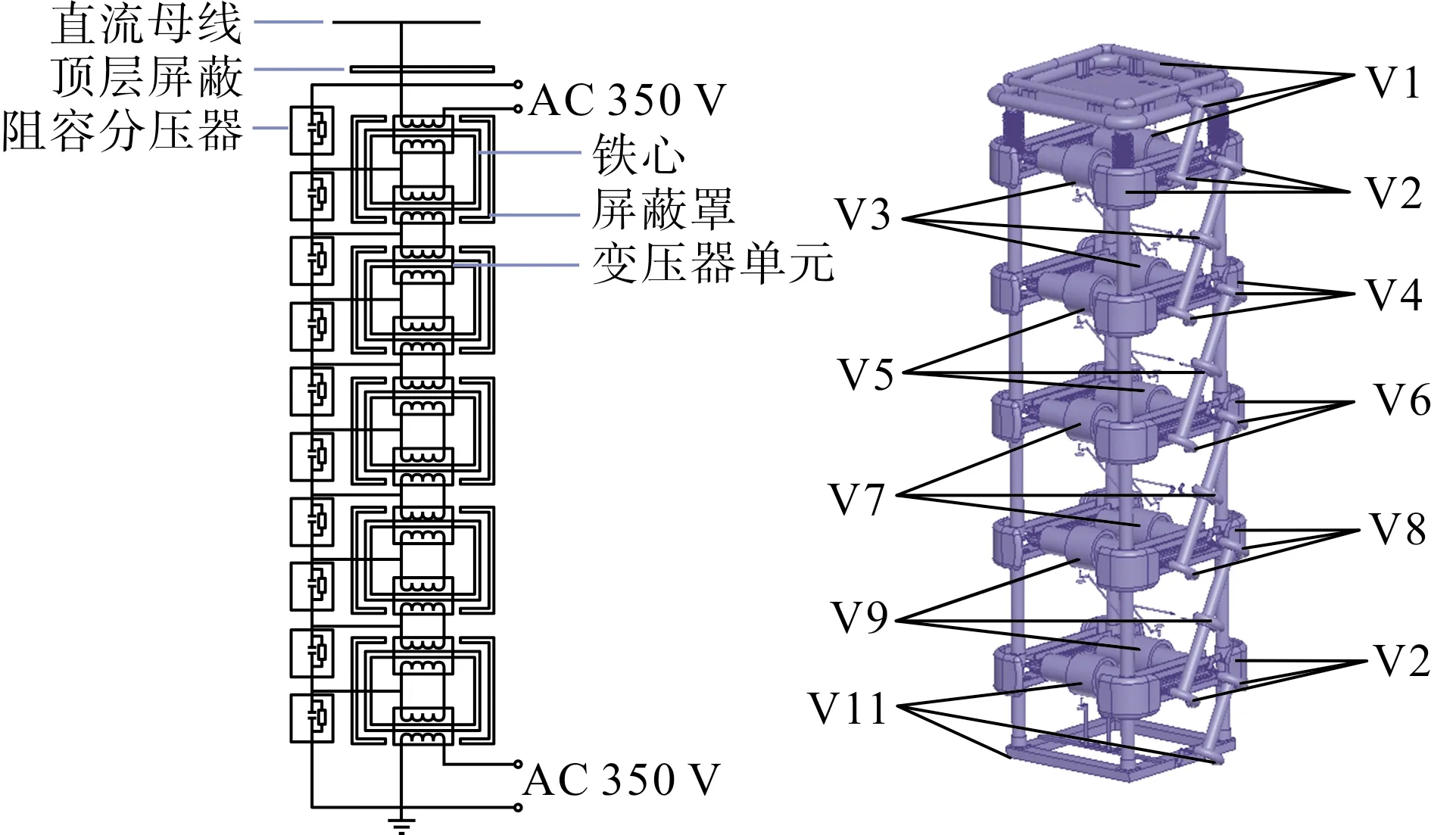
图5 供能变压器各层电位加载图

由于本文研究的供能变压器电场集中在上层，因此对上层的剖分要更为精细，同时整个设备需要外包多层空气，逐级剖分，从内至外逐渐加粗网格，在保证设备表面电场强度计算准确的前提下，减小计算量，提高计算效率。上层的网格剖分如图6所示。

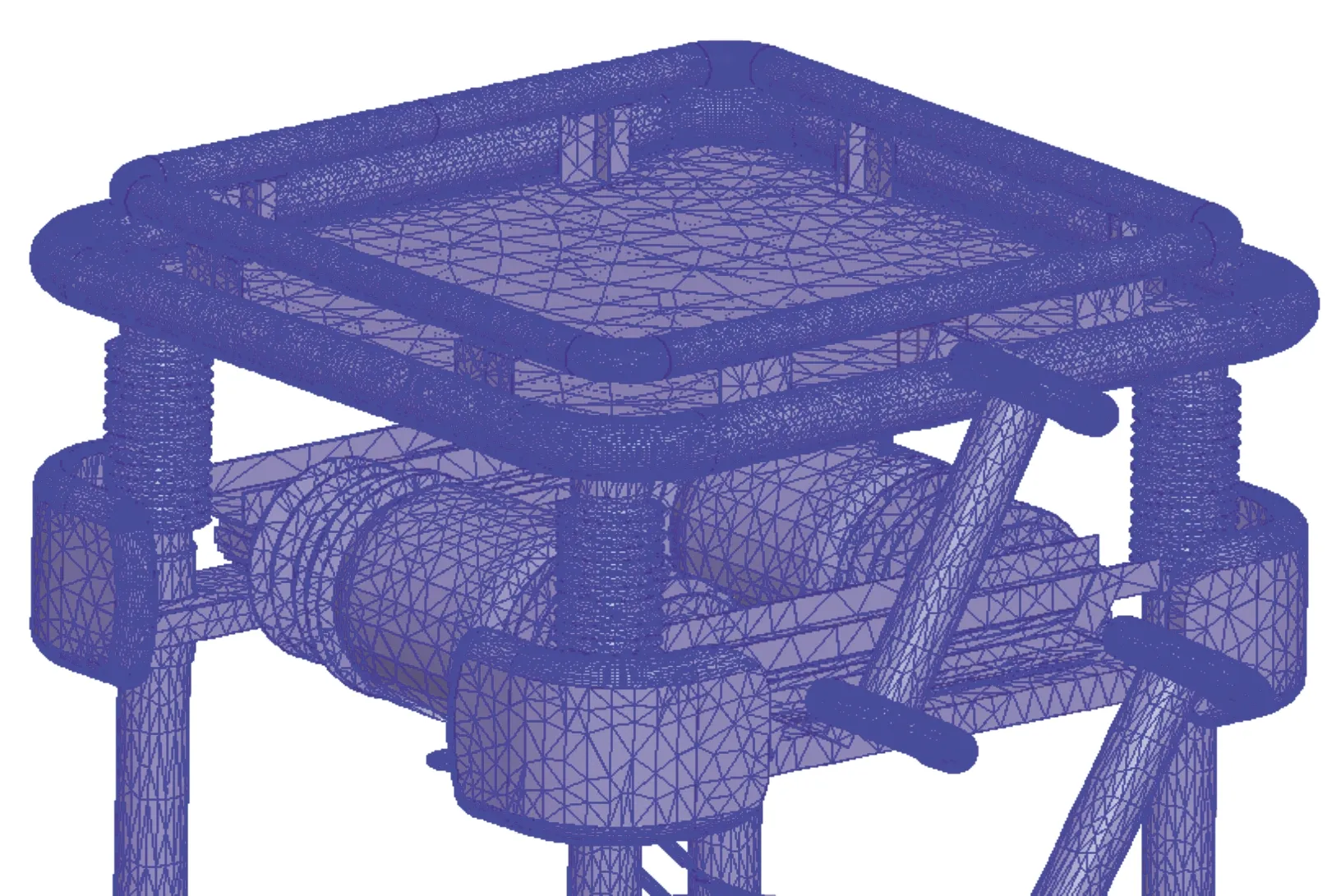
图6 供能变压器上层网格剖分图

3 结果对比与分析

3.1 静电场

静电场下得到供能变压器的电压分布和电场分布云图如图7所示。

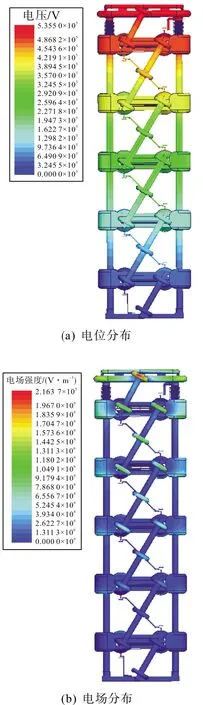
图7 供能变压器静电场仿真结果图

由图7可得，供能变压器的电位和电场均从上至下逐层递减。因此本文主要研究最上层的电场分布，只要上层各部分满足电场限制值的要求，则整体也满足要求，该供能变压器上层主要部分电场分布如图8所示。

图8 供能变压器上层主要部分电场分布图

其中，顶层屏蔽表面最大电场位于其上下均压环拐角处；屏蔽罩表面最大电场也位于其拐角处，阻容分压器表面最大电场位于其上均压环；支柱绝缘子表面最大电场位于最上层伞裙端部；变压器套管表面最大电场位于靠近中间圆柱部分两侧的伞裙端部。

3.2 恒定电场

由于恒定电场分析的结果会受到空气电导率的影响，令空气电导率在1×10-16～1×10-12S/m范围内变化，可得隔离变压器最上层主要部分表面最大电场与空气电导率之间的关系如图9所示。

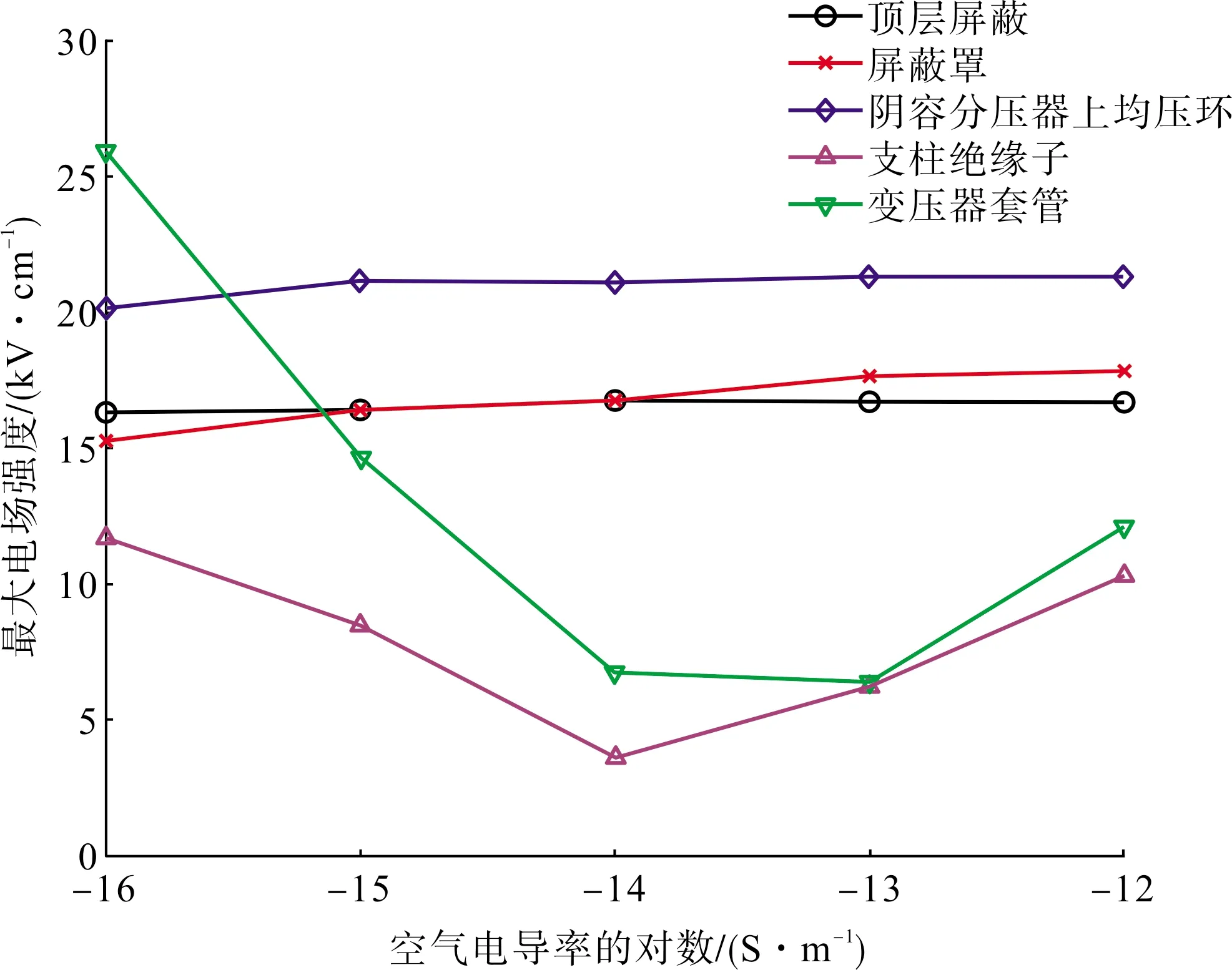
图9 供能变压器最上层主要部分电场分布图

由图9可得，作为导体的顶层屏蔽、屏蔽罩与阻容分压器上均压环表面的最大电场强度几乎不随空气电导率的变化而变化。其中，屏蔽罩的电场强度变化最大，但是幅度也不超过6.3%。

作为绝缘材料的支柱绝缘子与变压器套管的表面最大电场强度随着空气电导率的增加而先减小后增大，变化明显，在空气电导率与支柱绝缘子电导率接近时出现最小值。其中，变压器套管的电场强度变化最大，空气电导率为10-16S/m时的最大场强为10-14S/m的3倍以上。由于支柱绝缘子和变压器套管表面最大电场都位于其伞裙的端部，因此通过本文1.2节的分析可知，上述现象与支柱绝缘子和变压器套管的伞裙结构有关。

3.3 对比分析

供能变压器静电场与不同电导率下恒定电场的仿真结果如表2所示。

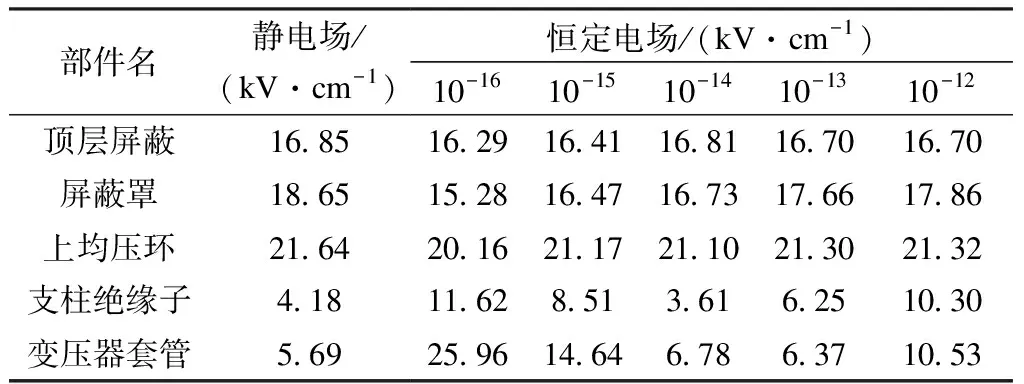
表2 供能变压器最上层各部分最大电场值

可以看到，对导体材料来讲，静电场与不同空气电导率下恒定电场的计算结果相差不大，静电场计算结果要略大于恒定电场，为了在设计时留有一定的裕度，推荐选择静电场作为导体材料金具起晕电场校核的电场类型。

对绝缘材料来讲，两种场的计算结果相差较大，不同电导率下的恒定电场结果也有明显差异，因此选择恒定电场作为绝缘材料电场校核的电场类型更为恰当，同时需要选择较为干燥情况下的空气电导率10-16S/m和较为湿润情况下的空气电导率10-12S/m计算结果中的最大值作为绝缘设计的参考最大电场。

3.4 起晕电场校核

电晕放电是影响电力装备电磁环境的主要因素，因此对上层金具进行起晕电场计算。顶层屏蔽表面最大电场位于其上下均压环拐角处；屏蔽罩表面最大电场也位于其拐角处，仅以拐角处而言，也可当做均压环处理；阻容分压器表面最大电场位于其上均压环。可以发现，最大电场都位于均压环处，而均压环的起晕电场可以通过Peek公式推导出[23-24]，直流形式的Peek公式为:

(12)

式中：Eonset为标准大气条件下导线的表面起晕电场；δ为空气相对密度；r为管径；m为反应导线表面状况的粗糙系数；E0和k分别为两个经验常数，在标准大气压下，负极性的E0一般取31.0，k取0.308。考虑到均压环局部发生电晕，均压环相对导线来说比较光滑；环形的起晕场强比管形起晕场强要大。再综合考虑过载倍数，这里将表面粗糙系数m定为0.8，得到的隔离变压器最上层各部分金具的起晕场强控制值如表3所示。

表3 起晕场强控制值

对比表2的各部分的电场计算值与表3的起晕场强控制值可得，在±535 kV电压下该供能变压器正常工作时不会产生电晕。

4 结论

本文针对±535 kV直流断路器用隔离供能变压器的电场计算问题，通过绝缘材料伞裙结构分析了空气电导率对恒定电场的影响，提出了交直流混合复杂设备的电场校核原则，并使用该原则对隔离变压器进行了分析，得到了如下结论。

1)通过理论分析与伞裙简化模型实验，本文给出了交直流混合复杂电气设备的电场计算原则：既要进行静电场计算也要进行恒定电场计算，在恒定电场计算时，由于绝缘材料的伞裙结构，还需考虑空气电导率的影响。

2)恒定电场下考虑空气电导率的原因为：空气电导率易随着湿度的变化而变化，同时电气设备的绝缘材料多设计为伞裙结构，此结构端部的电场会随着空气电导率的增大先减小后增大，不同空气电导率下计算结果相差可达10倍以上，因此需要专门考虑。

3)按照本文给出的电场校核原则，完成了±535 kV隔离供能变压器的电场仿真，结果验证了理论分析的准确性。为了留有一定裕度，建议在进行导体金具起晕电场校核时，选择静电场计算结果；在进行绝缘性能设计时，选择恒定电场计算结果，同时要选择空气电导率在干燥情况下的10-16S/m和湿润情况下的10-12S/m中的最大值作为参考最大电场。

4)对该供能变压器上层区域的导体金具进行了起晕电场校核，结果表明在其正常工作时不会产生电晕。