高压交流输电线路下方有限大金属屏蔽网的电场屏蔽效能

徐禄文，杨勃，刘彤

(1.国网重庆市电力公司电力科学研究院，重庆401123；2.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系)，北京100084)

0 引言

输电线路临近或跨越居民区时，可能存在部分区域电场强度超标的问题或误触导体触电的问题。针对这2种问题，需要对输电线路附近的工频电场进行改善。而较为有效的一种改善方式就是局部架设接地金属屏蔽导体或者屏蔽网。

目前对于金属屏蔽导体屏蔽效能的计算方法有理论公式法、经验公式法和数值计算方法等[1-5]，但理论公式法和经验公式法只适用于无限大或者半无限大金属屏蔽网，且对理论公式法与数值仿真计算方法所得结果之间的对比尚未有相关研究。此外，采用数值计算方法计算屏蔽网的屏蔽效能时，多采用有限元仿真软件计算或者模拟电荷法计算，当需要反复移动屏蔽网以测试其对某一特定区域的屏蔽效能时，反复建模的计算量大且耗时长，因此须对该方法做出进一步改进。

目前，国内外对无限大和半无限大金属网的屏蔽效能有较多研究，而对于有限大金属网屏蔽效能的求解目前尚无适用的公式，一般采用商用软件仿真计算[3-4]。此外，对于仿真方法与理论方法计算结果的对比也尚无相关研究。文献[3]用CDEGS软件仿真计算了接地金属网对高压输电线路附近居民屋内的电场强度屏蔽效果。文献[4]通过ANSYS仿真研究得出通过优化屏蔽设备架设位置可以大幅度提高屏蔽性能。文献[5]基于模拟电荷法和矩量法研究了屏蔽线(网)屏蔽效能的影响因素。若要优化屏蔽设备的屏蔽性能，离不开对屏蔽设备在不同位置下屏蔽效果的反复计算。而在上述应用中，若移动金属网的位置或改变金属网的结构则需要重新对庞大的输电线路模型进行三维建模，存在计算量大、计算效率低的问题。若要提高计算效率，则须提出更加高效的、适用于反复计算的数值计算方法。

本文首先介绍了计算输电线下金属导体电场屏蔽效能的经验公式方法，指出了该方法的缺点，并采用模拟电荷法[6-19]对输电线路和屏蔽网组成的系统进行了统一建模，并给出了相应的简化方案，最后对屏蔽网屏蔽效能的影响因素进行了研究，包括金属网的结构、疏密程度以及导体粗细对屏蔽效能的影响，研究成果可以为实际工程中屏蔽网的设计提供指导。

1 电磁屏蔽效能的计算方法简介

1.1 无限大与半无限大屏蔽网的屏蔽效能计算

用屏蔽系数S来表征屏蔽网的屏蔽能力，其表达式为：

(1)

式中：Es为屏蔽后的电场强度；Eu为屏蔽前的电场强度。同时，也可使用屏蔽效能PSE来表征金属网的屏蔽能力，屏蔽效能PSE的表达式为：

(2)

显然，屏蔽系数和屏蔽效能都可以表示金属网对高压输电线路电场的屏蔽作用，在实践中这2个概念都有使用。

对于平行于地面、平行于输电线路且由间距相等的平行线导体组成的无限大接地金属屏蔽网，如图1所示，其屏蔽效能PSE∞的计算公式[1]为：

(3)

式中：H为金属网距离地面的高度；S为导体之间的间距；R为导体的半径。如果金属网不是无限长的，那么其屏蔽效能在式(3)的基础上再乘以边缘系数f(x/H)，x为待求点距离金属网边缘的距离。在垂直线路方向上有限大而在平行输电线路方向上无限大的半无限大屏蔽网屏蔽效能的表达式为：

PSE(x)=PSE∞×f(x/H)

(4)

式中：边缘系数f为x/H的函数，可以通过查阅曲线取得[1]。根据图1和式(4)可知，经验公式法所获得的屏蔽效能为无限长情况下的结果。因此，式(4)的结果仅仅在屏蔽网中心才有意义。

图1 输电线路与平行线式接地金属网

对于有限大小金属网屏蔽效能的评估，应考虑感应电荷分布的不均匀性，因此，无法采用解析公式直接计算，需通过合理的数值方法进行计算。

1.2 模拟电荷法计算有限大屏蔽网的屏蔽效能

图2为架设有限大屏蔽网后的输电线路模型示意图，输电线路及屏蔽网系统的静电场边值问题为：

图2 输电线路与金属网模型示意图

(5)

式中：φ|PowerLine为输电线路表面电位；φ|MetalMesh金属网导体表面电位；Vp和Vs分别为输电线路导线对地电位和金属网导体表面对地电位；Γ∞为无穷远边界；φ|Γ∞为无穷远边界处的电位。

采用模拟电荷法对输电线路和金属屏蔽网建模，列出模拟电荷方程，并写成式(6)的矩阵形式。

(6)

式中：Kpp为输电线路单元之间的自电位系数矩阵，表示输电线路单元之间的耦合关系；Kss为接地金属网单元之间的互电位系数矩阵，表示金属网单元自身的耦合关系；Kps和Ksp分别为输电线路单元与金属网单元之间的互电位系数矩阵，表示输电线路与金属网之间的耦合关系，Ksp=KpsT；qp为输电线路单元电荷的nc维列向量；qs为金属网单元电荷ns维的列向量；Vp为ns个位于导线表面的匹配点处的电位列向量；Vs为nc个位于金属网表面匹配点处电位列向量，由于金属网接地，Vs实际上为零向量。

在实际应用中，屏蔽网对输电线路导线上电荷分布的影响微乎其微，因此可以忽略该影响，即认为Kps= 0，因此，式(6)可简化为：

(7)

式(7)实现了输电线路和屏蔽网间的电磁“解耦”，输电线路的电荷只需计算一次即可。而屏蔽网的电荷可根据位置的变化只计算Ksp。

求解式(7)即可得到qp与qs，从而采样面内任意采样点Pi的电位φ(Pi)可通过叠加定理求出，如式(8)所示。

φ(Pi)=KPP(P,Pi)qp(P)+KPS(P,Pi)qs(P)

(8)

式中P为qp与qs的源点。对式(8)两边求负梯度，可以得到金属网在采样点Pi处的电场强度。然后采用式(1)或式(2)可计算出相应的屏蔽系数或者屏蔽效能。

2 数值算例

2.1 计算方法正确性验证

本节分别使用传统模拟电荷法和迭代型模拟电荷法计算采样线的电场强度，并求出2种算法的相对误差。

交流单回输电线路附近架设均匀网格状接地金属网，计算该金属网的屏蔽效能。算例布置俯视图和正视图如图3—4所示，输电线路和金属屏蔽网参数此处从略。

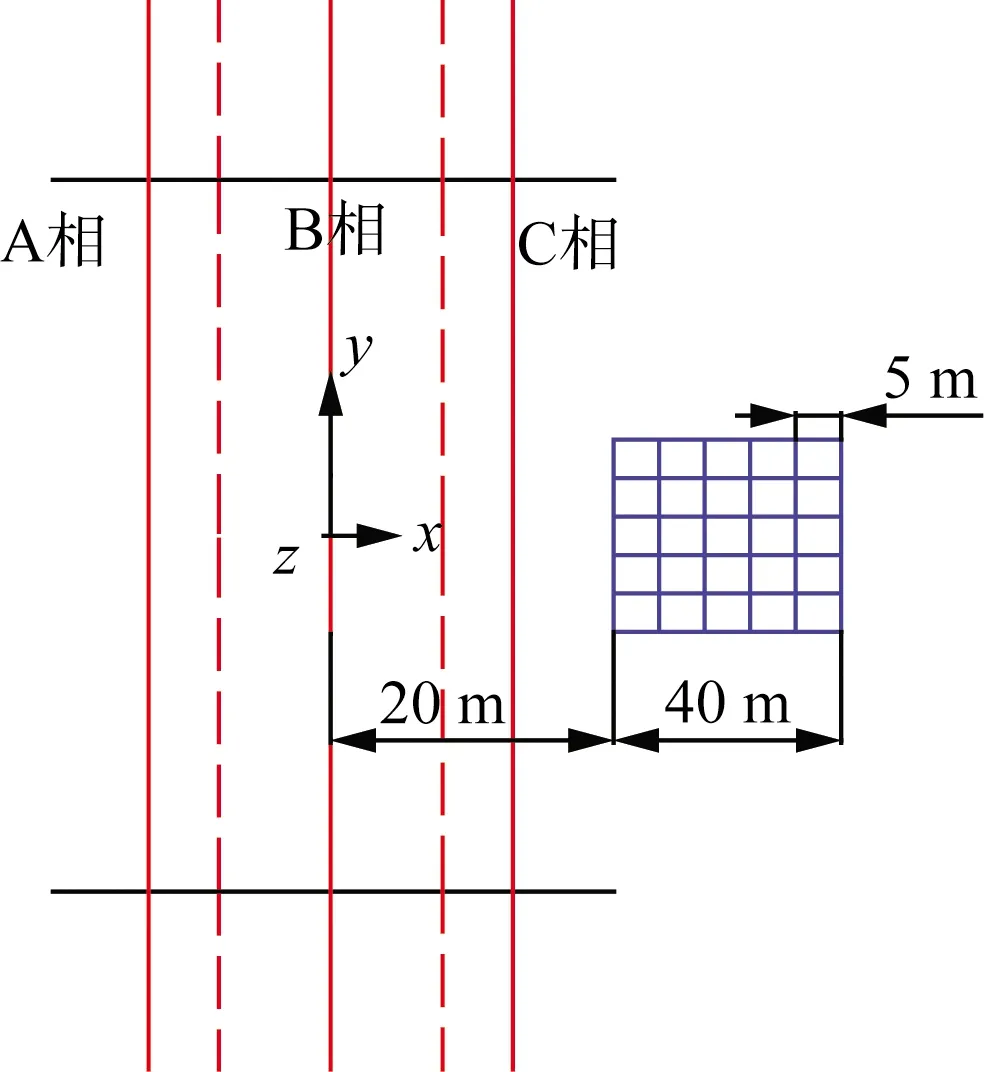
图3 算例模型俯视图

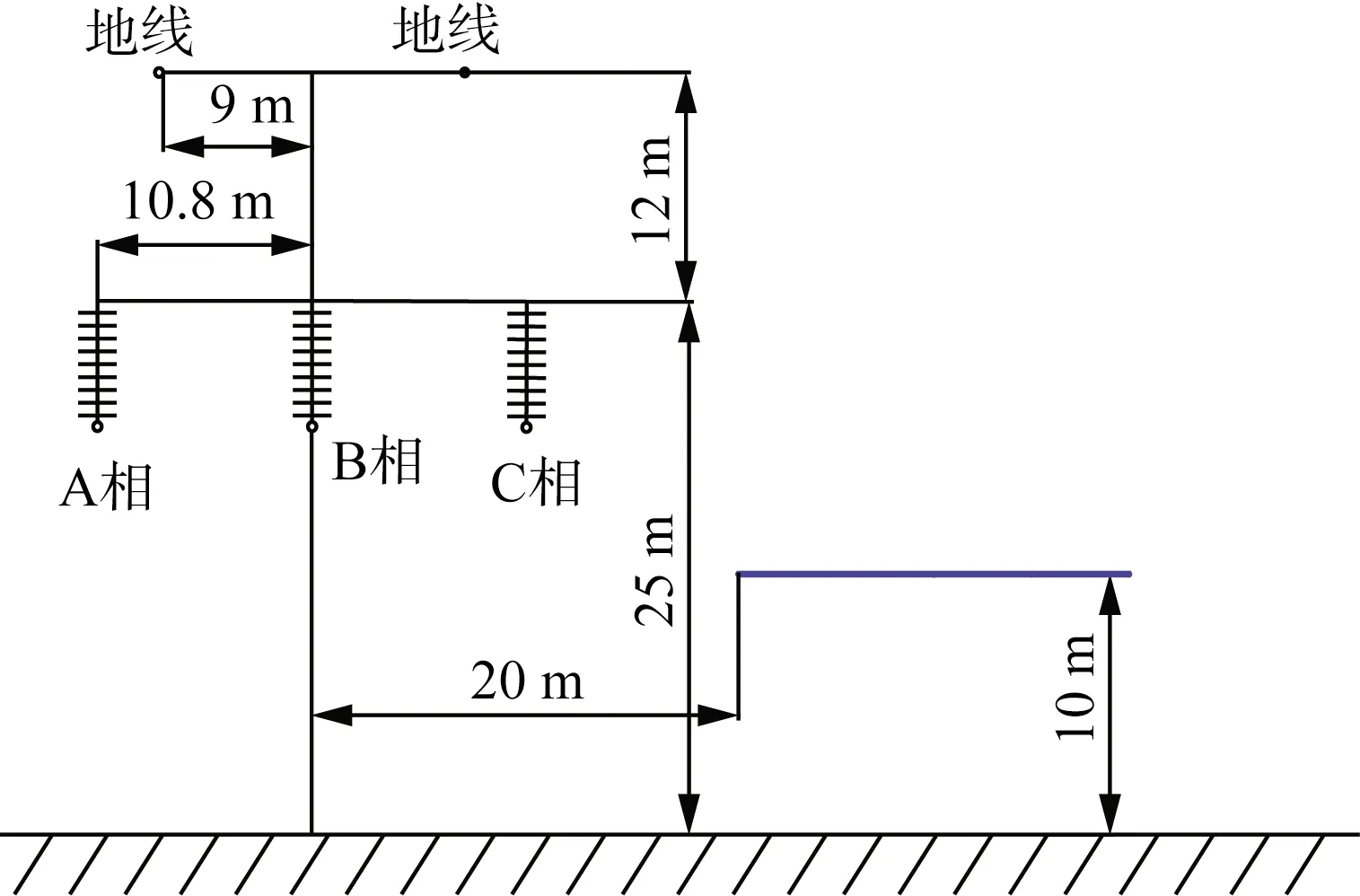
图4 算例模型正视图

分别采用2种方法计算金属网正下方高度为1.5 m，y=0 m, 沿x轴方向的电场强度，计算结果如图5所示。

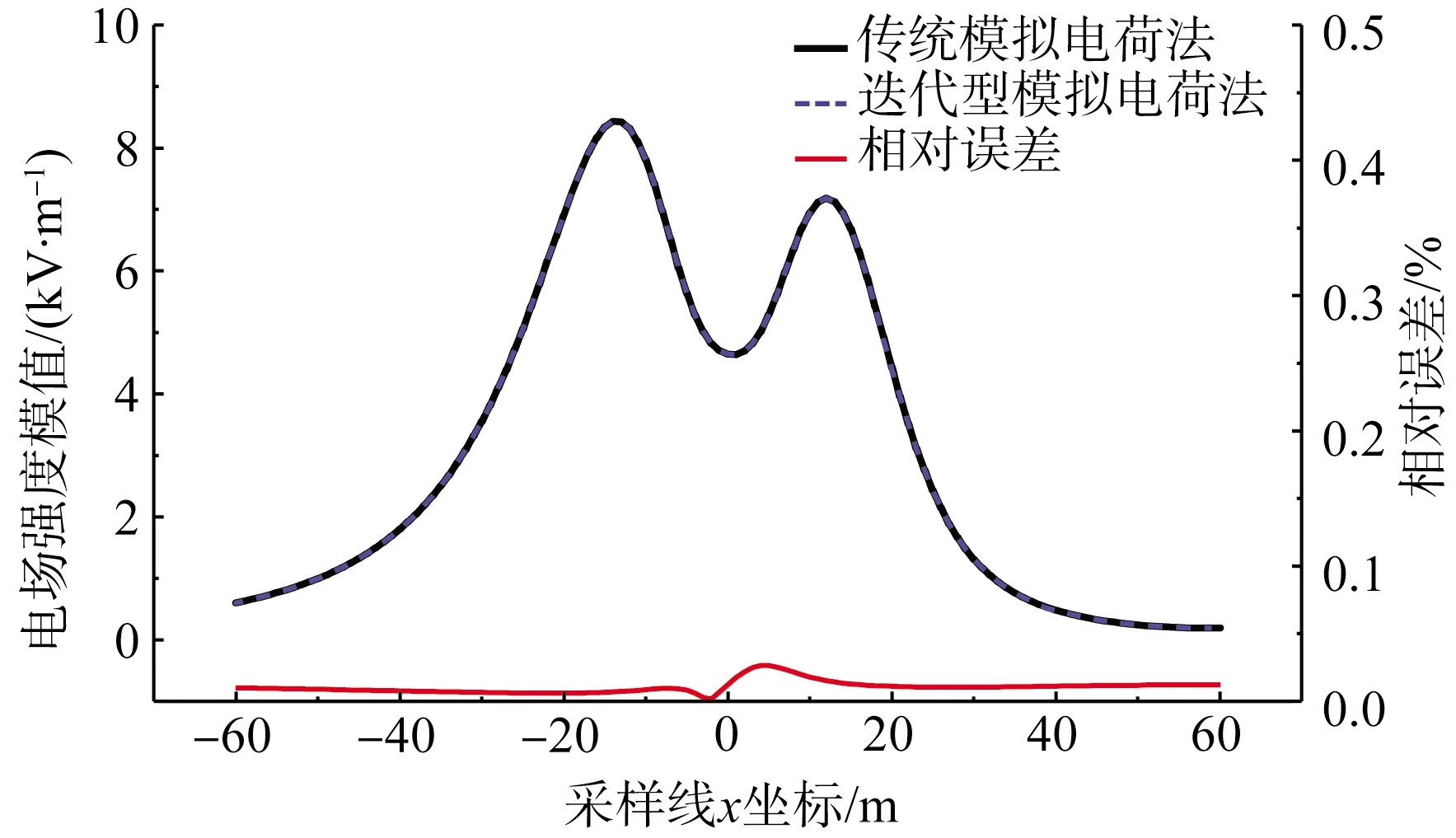
图5 y=0 m, z=1.5 m处采样线上电场强度幅值

由图5可知，2种计算方法的计算结果几乎一致，相对误差不超过0.1%。从计算时间的角度，本文迭代算法的计算时间是传统算法的30%。

2.2 屏蔽网屏蔽效能影响因素分析

对于屏蔽网的屏蔽效能的影响因素进行对比分析，首先比较几种常见结构的金属屏蔽网的屏蔽效果，然后研究金属网的疏密程度以及导体粗细对屏蔽效果的影响。

图6—9分别为4种不同类型的1—4号屏蔽网。图6中1号金属网为平行于地面的网格状屏蔽网。

图6所示输电线路附近有一个60 m×40 m的停车场，图中采样面区域离地面1.5 m高处的电场强度超过4 kV/m，需要通过在其上方架设金属屏蔽网来改善。

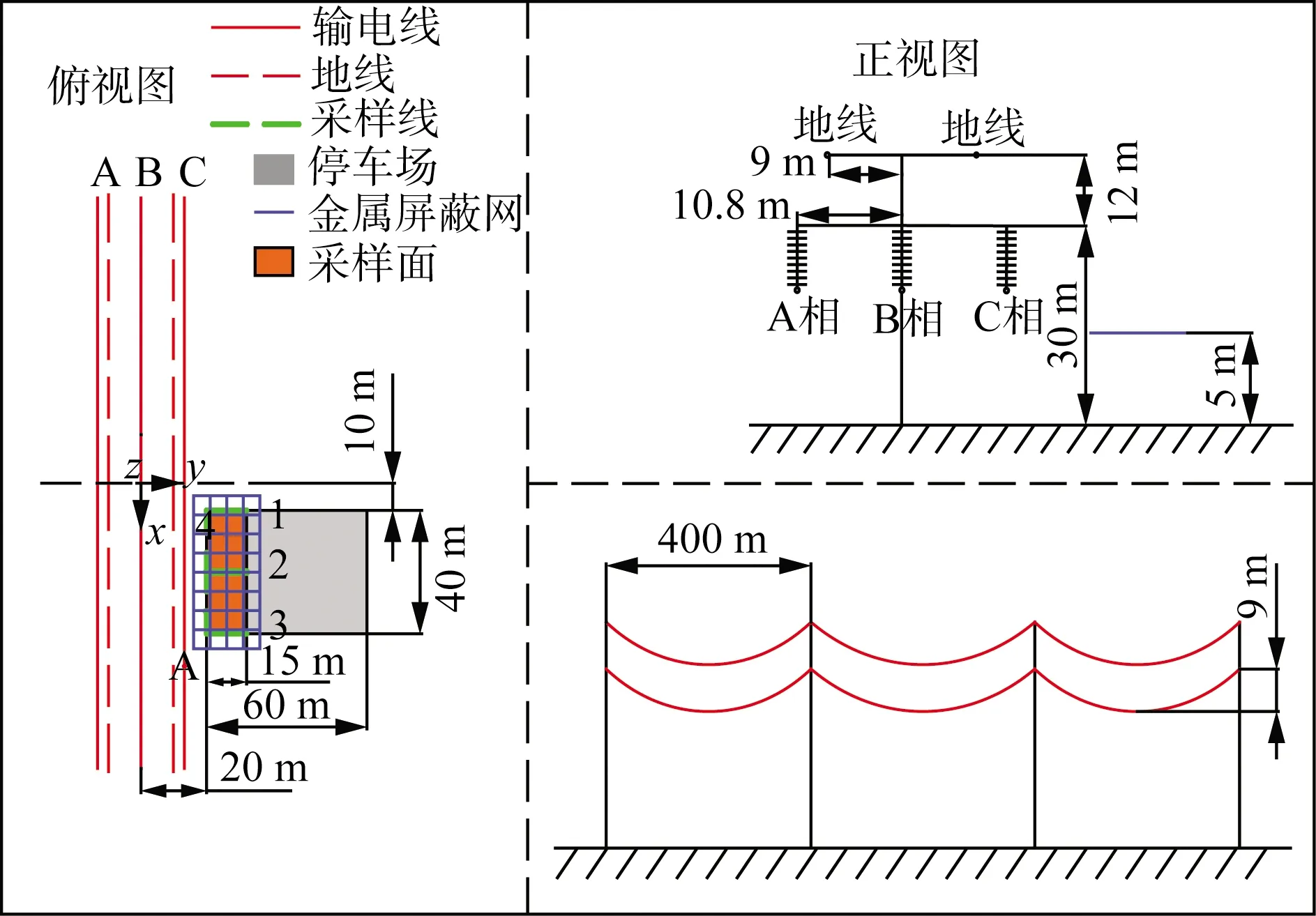
图6 1号金属屏蔽网对输电线路附近停车场的屏蔽示意图

图7中2号金属网为平行于地面的平行线状屏蔽网。

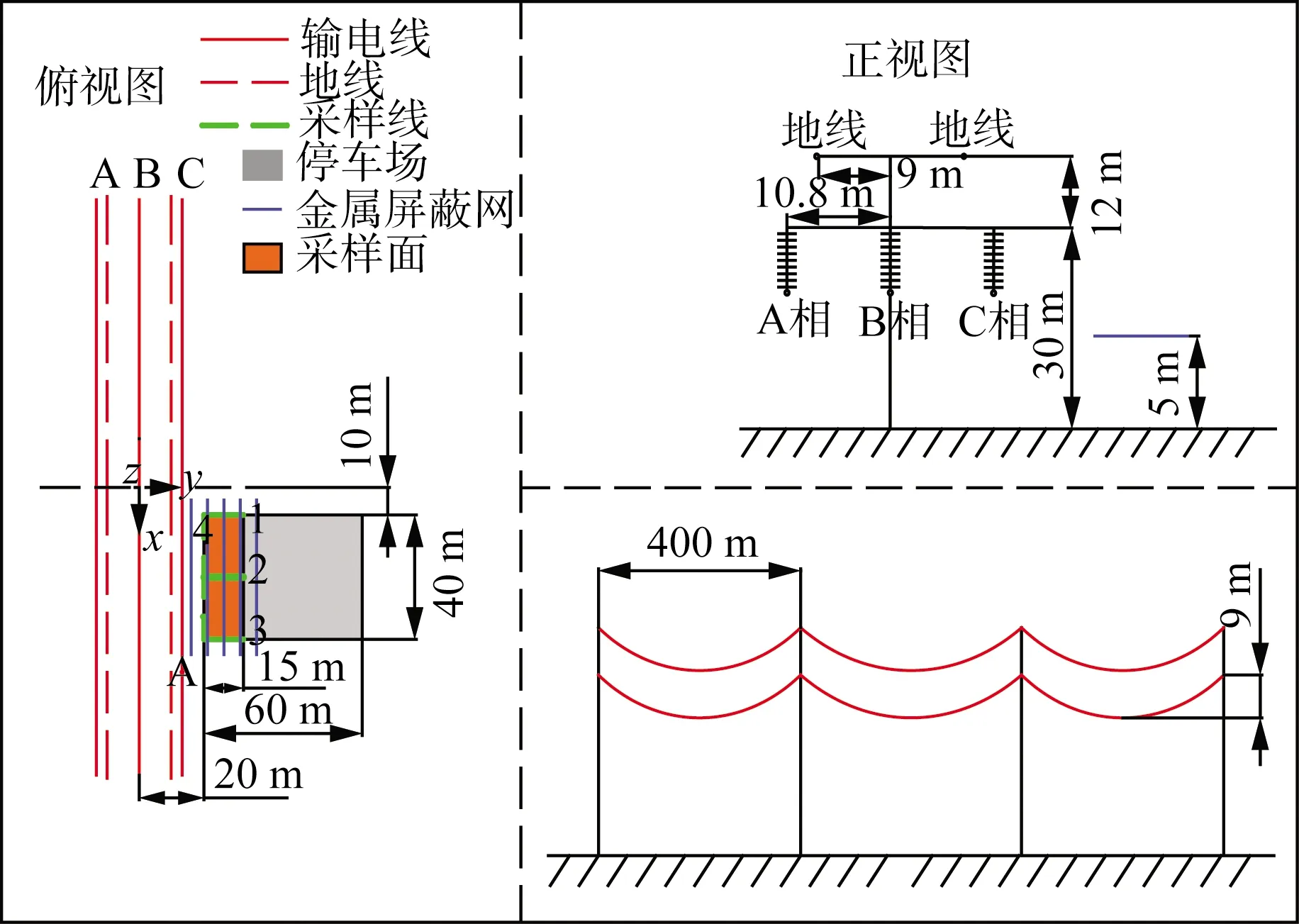
图7 2号屏蔽网对输电线路附近停车场的屏蔽示意图

图8中3号金属网为垂直于地面且平行于输电线路的一组平行线状屏蔽网。导体的疏密程度会对金属网的屏蔽效果产生影响。对于平行线状的2号金属网，屏蔽效能的变化如图8所示，当网格根数从5根扩大到10根、20根时，可以看出，导体加密一倍时，屏蔽后的电场强度近似地缩小一倍。当导体密集到一定程度时，理论上屏蔽后的电场强度将趋于一个稳定值，一般情况下，通过加密网格，可以对屏蔽效果有较为明显的增强。

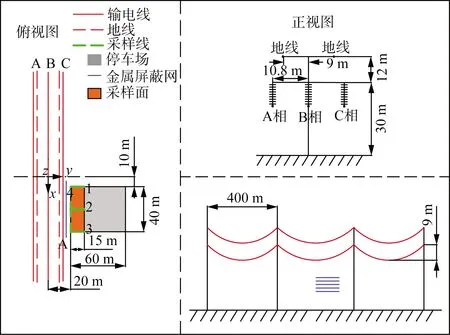
图8 3号金属屏蔽网对输电线路附近停车场的屏蔽示意图

图9中4号金属网为不规则屏蔽网。

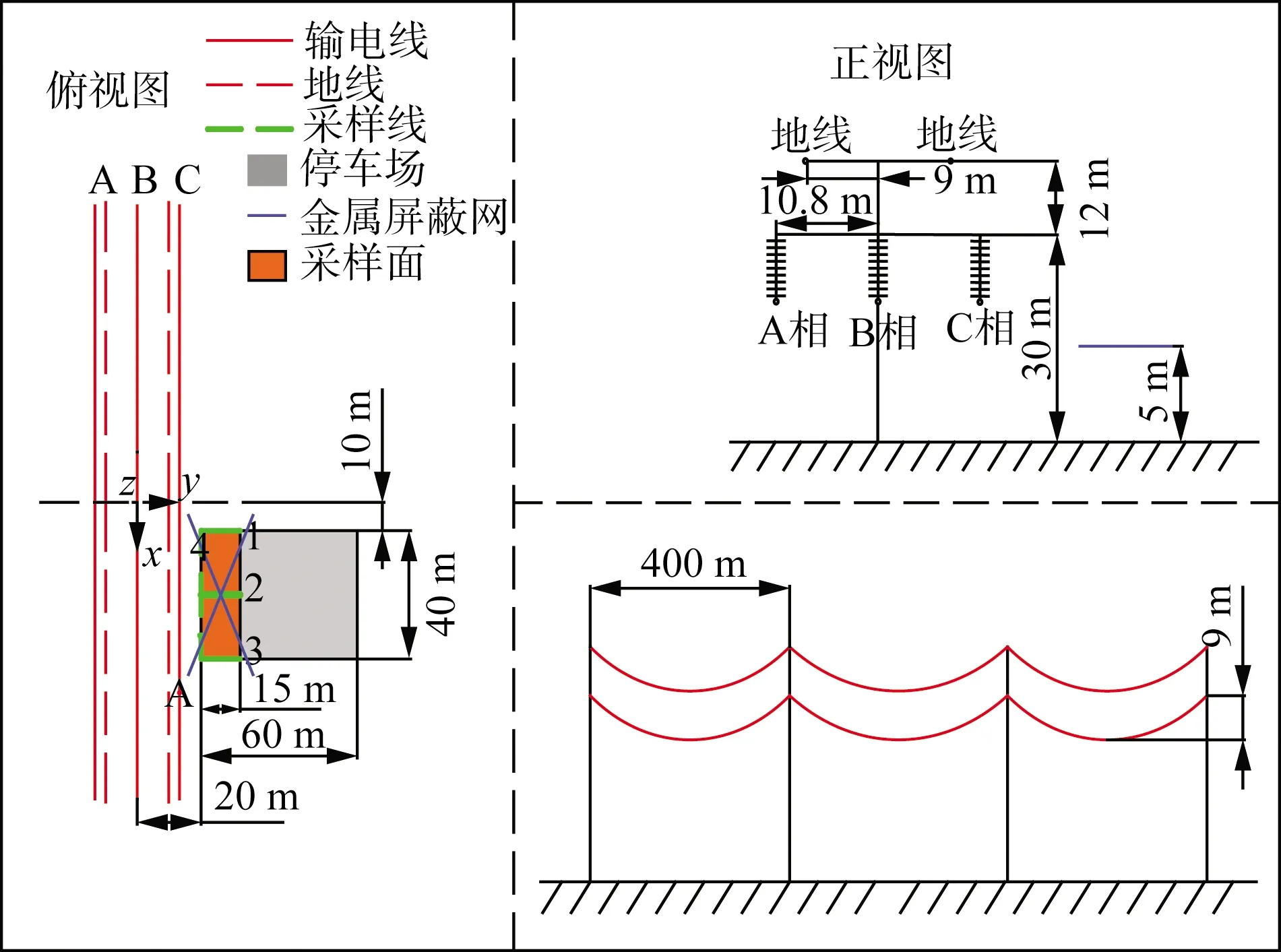
图9 4号金属屏蔽网对输电线路附近停车场的屏蔽示意图

图10为采样线1屏蔽前后的电场强度对比，反映了4种屏蔽网布置方式对屏蔽系数的影响规律。

从图10可以看出，网格状的屏蔽网用铁量最大、导体分布较为密集，其屏蔽效果最佳；而交叉式屏蔽网用铁量最少、导体分布比较稀疏，其屏蔽效果最差。所以不同结构的屏蔽网屏蔽效果不同，随着用铁量和导体的密集程度的增加而增加。

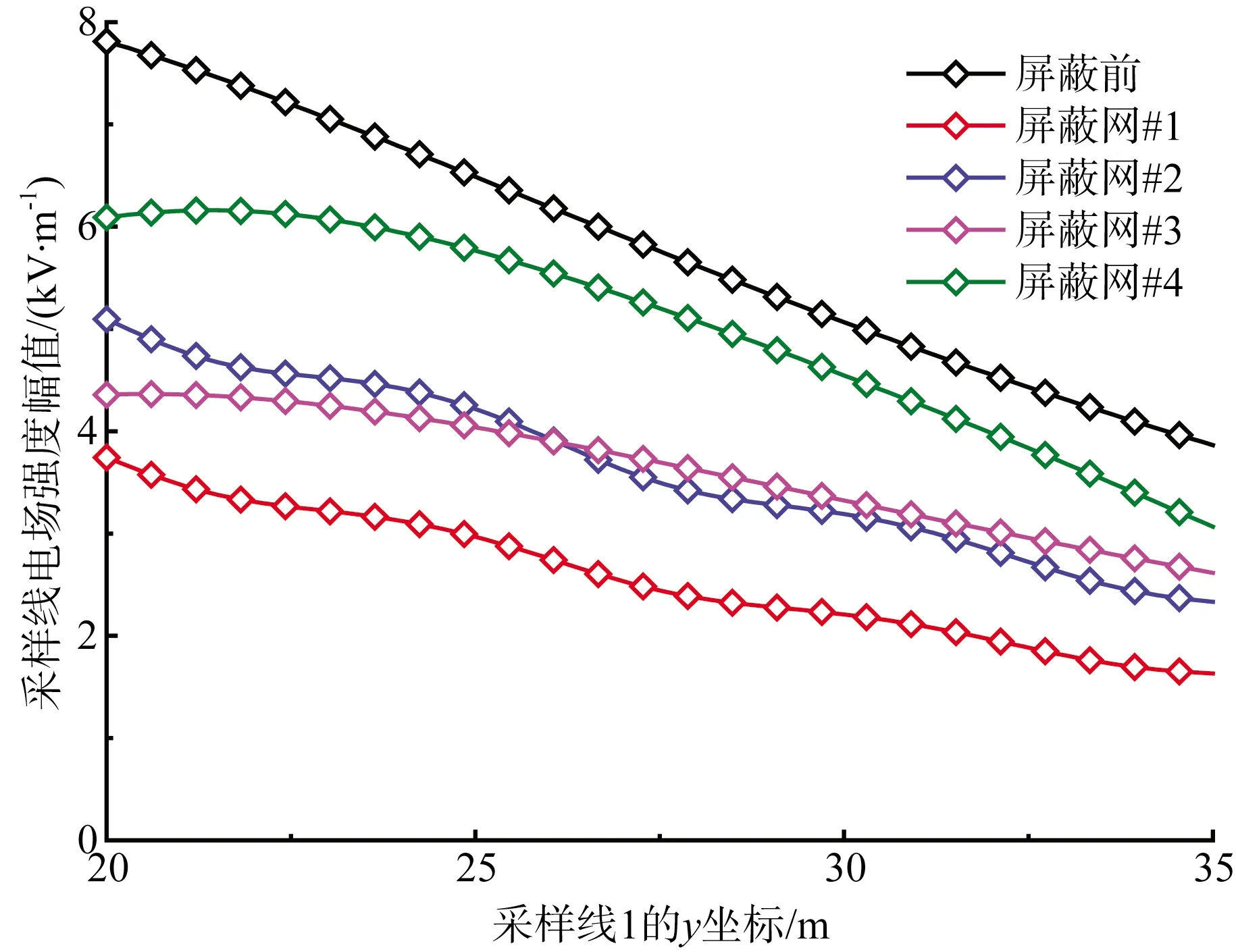
图10 1号采样线屏蔽前后的电场强度对比

金属屏蔽网的疏密程度也会对其屏蔽效果产生一定影响。以2号屏蔽网为例，不同疏密程度的屏蔽网对1号采样线的电场强度屏蔽效果如图11所示。当导体的根数由5根扩大到10根、20根、40根时，可以看出，金属屏蔽网的疏密程度对其屏蔽效果有一定影响，屏蔽网越密时，其屏蔽效果越好。

图11 不同疏密程度的2号屏蔽网对1号采样线电场强度屏蔽效果

屏蔽网的高度、总面积和导体总长度等参数均会影响屏蔽网的屏蔽效能。限于篇幅，不详细罗列。综合分析可知，金属屏蔽体用量是决定屏蔽效能的关键因素。

3 结语

考虑高压输电线路下方实际问题的场景，研究了金属屏蔽网屏蔽效能的快速简化计算方法，获得了屏蔽网布置方式、导体数目和导体半径等参数对屏蔽效能的影响规律，从而可以为工程实践中设置屏蔽网提供技术依据和支撑。

本文虽然是以棒状导体为研究对象展开论述的，对于面屏蔽和体屏蔽，所提方法可进一步推广应用。