基于椭球近似解析法的飞行器再入轨迹优化

张 凯 杨小龙 钟 震

北京宇航系统工程研究所，北京，100076

0 引言

为使飞行器跨越复杂的大气环境安全返回，满足多种约束的飞行器再入轨迹规划一直是研究热点[1]。按照是否跟踪标准轨迹，飞行器再入过程主要分为标准轨迹制导和预测校正制导两大类[2]。标准轨迹制导形式简洁跟踪稳定有较高应用价值[3]，如何设计标准轨迹是该方法的重要研究方向[4]。经典的阻力加速度设计方法在阻力加速度剖面内得到再入走廊，引入航程与阻力加速度的关系，将航程转化成再入走廊内分段阻力加速度曲线，大大简化了轨迹的设计流程，最早在航天飞机再入中获得成功应用[5]。文献[6]讨论了阻力加速度方法在低升阻比火星再入飞行器的应用，文献[7]将过程约束转化到再入走廊中，通过规划满足约束的阻力加速度速度剖面生成航天飞机参考轨迹，文献[8]将航天飞机的二维再入轨迹规划扩展到三维情况，采用基于降阶的运动方程和最优控制理论实现纵横向参考加速度的在线规划，文献[9]改进了传统阻力加速度剖面，采用两段折线与走廊边界快速设计标准轨迹，提高了标准轨迹制导方法的实时性，文献[10]将阻力加速度剖面与预测校正方法结合，由走廊上下边界插值获得标准轨迹，插值参数由预测校正方法确定，并在三维空间对标准轨迹进行校正，提升了再入飞行能力，文献[11]考虑了速度倾角约束，通过在阻力加速度-能量剖面终端加入速度倾角控制满足了速度倾角约束。

不同于现有文献直接采用阻力加速度的轨迹规划方法，本文推导了根据阻力加速度曲线快速计算再入段轨迹所需控制能力的公式，分析了再入段航迹倾角与阻力加速度曲线的关系，可以根据再入航迹倾角约束规划相应的曲线，保证飞行器在再入初始段和结束段满足相应约束，提出了将原轨迹阻力加速度剖面线性化的方法，并在此基础上提出了一种基于椭球近似解析的优化算法，根据该算法可以将标称轨迹修正为与其控制能力匹配的轨迹，通过仿真验证了算法的有效性。

1 飞行器再入模型

设飞行器再入过程中地球为圆球，飞行器为刚体，主要受气动升力、气动阻力和引力作用，则飞行器三维的运动学、动力学方程描述如下[12]

(1)

其中r是飞行器地心距，r=R0+h，h是飞行器当前高度，R0为地球平均半径，ωe为地球自转角速度，θ、φ为经纬度，V为速度，γ为航迹倾角，ψ为航迹偏角，L、D为升力、阻力加速度，σ为倾侧角。

升力和阻力加速度的表达式为

(2)

整理可得

(4)

其中

(5)

设R为再入段航程，则有

(6)

根据上式可以通过V-D曲线、速度-航迹倾角曲线来预测航程。

2 飞行器控制力与再入倾角

(7)

其中

(8)

飞行器不同的再入倾角所引起的阻力加速度变化不同，同时，有些飞行器再入段结束时对航迹倾角有要求，如果采用单独的再入段航迹倾角调节控制，会增加轨迹设计的复杂性，因此需要找出航迹倾角与规划的V-D曲线之间的关系，保证所规划的轨迹满足航迹倾角约束。根据前文推导，将轨迹倾角表达式移项整理可进一步得到

(9)

其中等式右端所有的量都可知，因此当得到初始或终端航迹倾角时，就可以计算出初始、终端的V-D曲线的斜率。记

(10)

使规划曲线的初始段和结束段满足上述公式得到的斜率即可保证航迹倾角约束。

3 基于标称轨迹的线性化模型

再入段标称轨迹描述采用曲线-直线-曲线的三段式曲线，形式如下：

图1 阻力加速度曲线示意图

其具体规划方法本文不再详述。通过该方法规划的初始轨迹所需控制能力可能大大超过了飞行器的容许控制能力，传统方法在这种情况下需要不断修正V-D曲线，且不能保证所修正的曲线满足控制能力约束，理想的方法是修正该曲线使其所需控制能力在飞行器的控制能力极限之内。

线性伪谱法中将状态方程在标称轨迹附近线性化[13]，根据此思路，本文以标称V-D曲线为基础，考虑将控制力和V-D曲线的对应关系在小范围内进行线性化。求u对D的偏导数，得到V-D曲线附近Δu和ΔD之间的线性关系。将V-D曲线用一系列等距的V对应D的散点表示，V-u曲线同理。其求导运算(D对V的导数)用差分计算来替代，求一阶导数时，需要前后相邻的两个量，求二阶导数需要前后相邻的5个量。由于计算u时最多需要D对V的二阶导数，因此只需要计算u对其前后5个D值的偏导数即可，这5个偏导数的计算采用Matlab软件符号运算进行推导，不再展开结果。由于改变D导致的u的改变量可以表示如下

(11)

将V-D曲线分成等距的N个点，将全N个点都考虑进去，可得

(12)

将上式简记为A1x1=x2。其中

x1=[ΔD1…ΔDN]T，x2=[Δu1…ΔuN]T。

考虑增加航程约束、高度约束、航迹倾角约束如下，

(13)

分别简记为A2x1=b2、A3x1=b3、A4x1=b4。综合可得

(14)

式(14)记为Ax=b。变量x1、x2中元素为ΔDi、Δui，需满足如下约束

Dmin-Di≤ΔDi≤Dmax-Di
umin-ui≤Δui≤umax-ui

(15)

其中Di、ui为原规划曲线的阻力加速度、控制量，Dmax、Dmin为再入走廊的阻力加速上下限，umax、umin为控制能力的上下限，其含义为修正轨迹后保证新轨迹不超过再入走廊的边界，同时所需控制力不超过飞行器的控制能力极限。其中Dmax、Dmin、umax和umin也可根据实际情况进行调整。

4 基于椭球近似的解析优化算法

基于飞行器再入的标称轨迹得到控制能力和阻力加速度的线性关系即其应满足的约束，约束条件为

Ax=b，xmini≤xi≤xmaxi

(16)

其中矩阵A为(N+5)×2N矩阵，x为2N维列向量，b为N+5维列向量，2N>N+5。优化指标为

J=max(min(λi·dis(xi,Ui))i=1,2，…，2N)

(17)

λi为设置的权系数，其中

Ui=[xmini,xmaxi]

(18)

(19)

该优化指标的意义是让x的每个分量都尽可能的远离其取值范围的边界。

记满足约束条件中等式约束的x的解集为Ω1，记满足第二个约束的x的集合为Ω2，易知Ω2为凸集。该指标的意义是在集合Ω2中寻找一点x，使该点到Ω2边界的距离最远，若结合等式约束，则完整意义是在集合Ω1和集合Ω2的交集中寻找一点x，使该点到Ω2边界的距离最远。原指标为无法求导的非线性函数，因此考虑将原指标改写为可导函数。在二维空间中考虑原指标，如图2所示，Ω2的边界即原指标意义下的等值线，对等值线进行缩放，当与Ω1只有一个交点时，该点即原指标下的最优解。

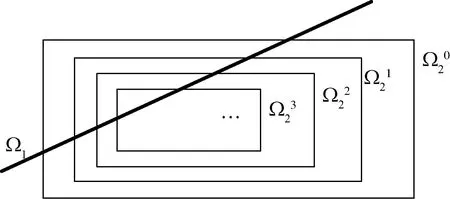
图2 原指标二维空间示意图

将原指标函数改写为可导函数，理论上改写后指标等值线越接近原指标等值线则优化结果越接近原指标，因此考虑将指标写为如下形式

(20)

其中a为自然数，a越大则其等值线越接近原指标的等值线，但函数形式也越复杂，求解时运算量也更大，因此采用a=1时的指标，如下

(21)

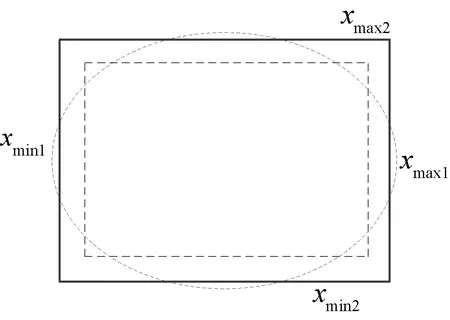
图3 二维空间示意图

图4 新指标与原指标等值线

如前所述，该优化问题的最优解即Ω1与等值线相切的点，Ω1为一仿射集，在Ω1与等值线相切的点处，等值线梯度方向垂直于Ω1，即垂直于Ω1对应子空间的基向量，由矩阵论相关知识可知，矩阵(I-A+A)中线性无关的列向量即Ω1对应子空间的基向量。最优指标等值线梯度为

(22)

其中

(23)

由上式可知梯度是关于x的一次函数，因此满足下列方程的解即为最优解

(24)

整理可得

(25)

其中

整理得

(26)

该方法可直接求最优解。解出新轨迹后可计算优化后的轨迹航程R′，如果R′与原轨迹航程差距较大，则更新b2，令b2=b2+R′-R，再计算上式解出x，重复1-3次即可。

本文中制导控制方法采用PID控制，方法如下

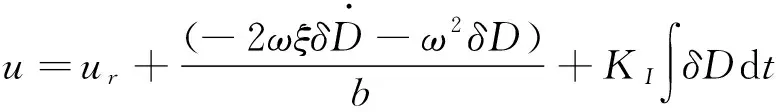
(27)

其中ur为参考轨迹的标称控制量，解算出σ即可，Dr是参考阻力加速度，δD=D-Dr。

5 仿真

为了验证本文方法的有效性，根据某参考对象数据进行仿真验证，速度-攻角曲线如图5。

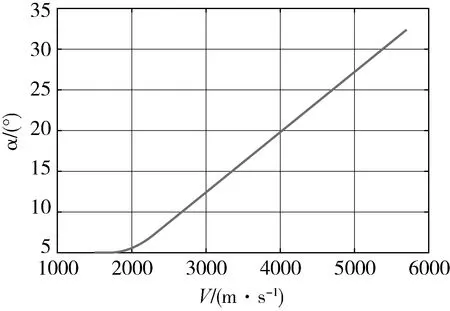
图5 再入攻角曲线

5.1 再入倾角范围

设再入高度为60km，阻力加速度为4m/s2，再入速度为5380m/s，则不同的再入倾角对应的初始V-D曲线的斜率如下图

图6 再入初始段轨迹倾角与V-D曲线斜率

由图中可知，再入初始段V-D曲线斜率随再入倾角变化比较剧烈，当再入倾角比较大时，V-D曲线的斜率为负，随着再入倾角的减小，V-D曲线斜率也不断减小，但是当再入倾角进一步减小到-20°以下时，在某个再入倾角下V-D曲线斜率突变为正，这是由于高空再入倾角进一步减小的时候，由于阻力加速度比较小，沿速度方向重力加速度的分量大于阻力加速度，这会导致初始再入段飞行器的速度增加、阻力加速度增加，反映在V-D曲线斜率上即斜率为正。

设再入段结束时刻阻力加速度为50m/s2，速度为1800m/s，则不同的轨迹倾角对应的末端V-D曲线的斜率如图7。

图7 再入末段航迹倾角与V-D曲线斜率

结束时刻阻力加速度一般比较大，重力加速度分量不会改变速度变化方向，由图中可见此时的V-D曲线斜率随轨迹倾角的变化在一个小范围内线性变化。根据以上仿真结果，再入时刻的轨迹倾角取0°～-10°，再入结束时刻的轨迹倾角范围可以大一些。

5.2 优化算法的有效性验证

初始段轨迹规划时Vd-Vc∶Vc-Vb∶Vb-Va=1∶2∶1，再入高度为60km，初始速度为4500m/s，再入初始段阻力加速度2.9m/s2，再入终点阻力加速度为50m/s2，终点速度为1800m/s，航程350km，再入倾角-1°，末端倾角0°，最大可用控制能力为控制能力极限的0.6倍。采样间隔为10m/s，航程迭代3次，运行环境为windos7，i5-6500，Matlab2017a，优化前后的曲线对比如下

图8 优化前后阻力加速度曲线

图9 优化前后需用控制力

图10 优化前后航迹倾角

优化前曲线的航程为350km，优化后为351.3km，可见航程误差小，线性化假设合理。通过上图可得知该方法保证了再入初始段和再入末段的航迹倾角满足约束，并改善了控制能力，使所需控制能力在飞行器控制能力极限之内。下面通过仿真跟踪优化前后的曲线验证优化算法的有效性，采用PD控制，其中控制参数的阻尼、频率分别选为1、0.8，可用的最大、最小倾侧角为175°、5°。优化前后的曲线跟踪仿真结果如下。

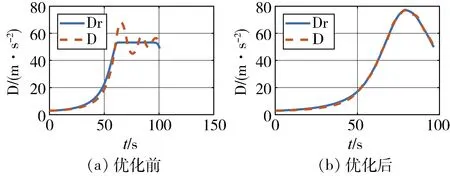
图11 阻力加速度曲线跟踪

图12 阻力加速度曲线跟踪误差

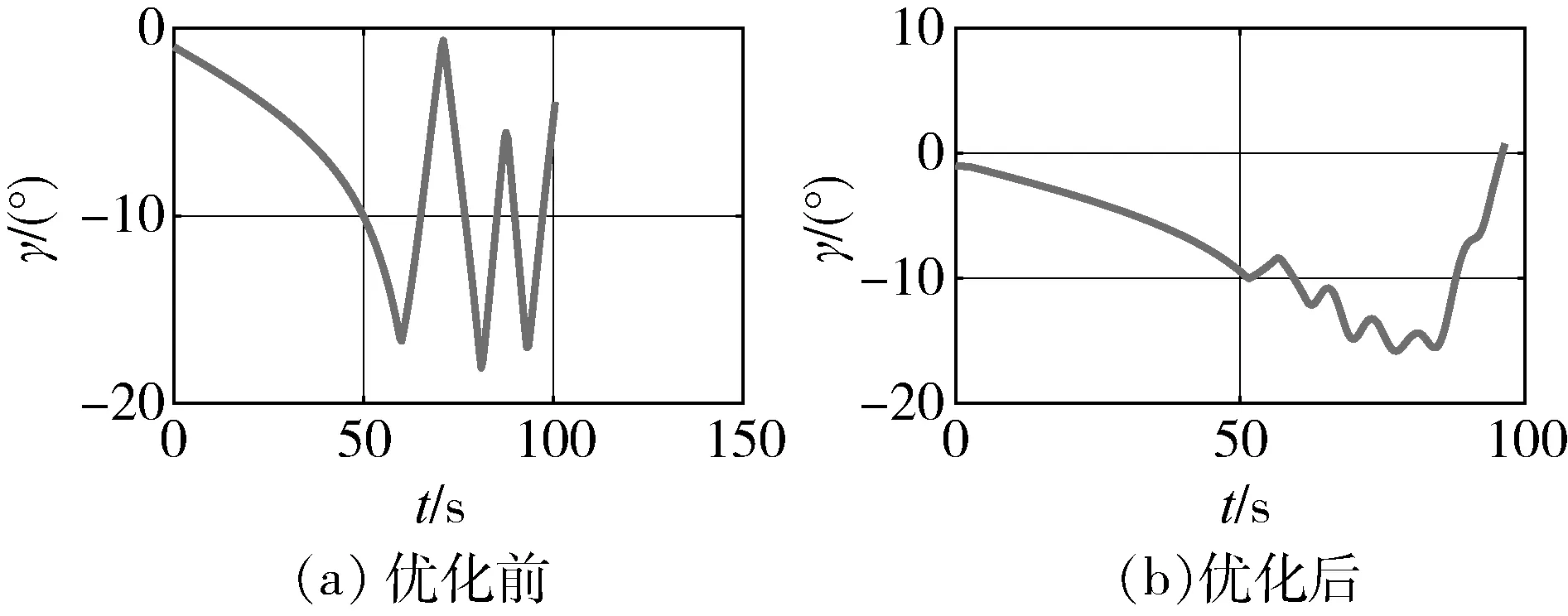
图13 航迹倾角

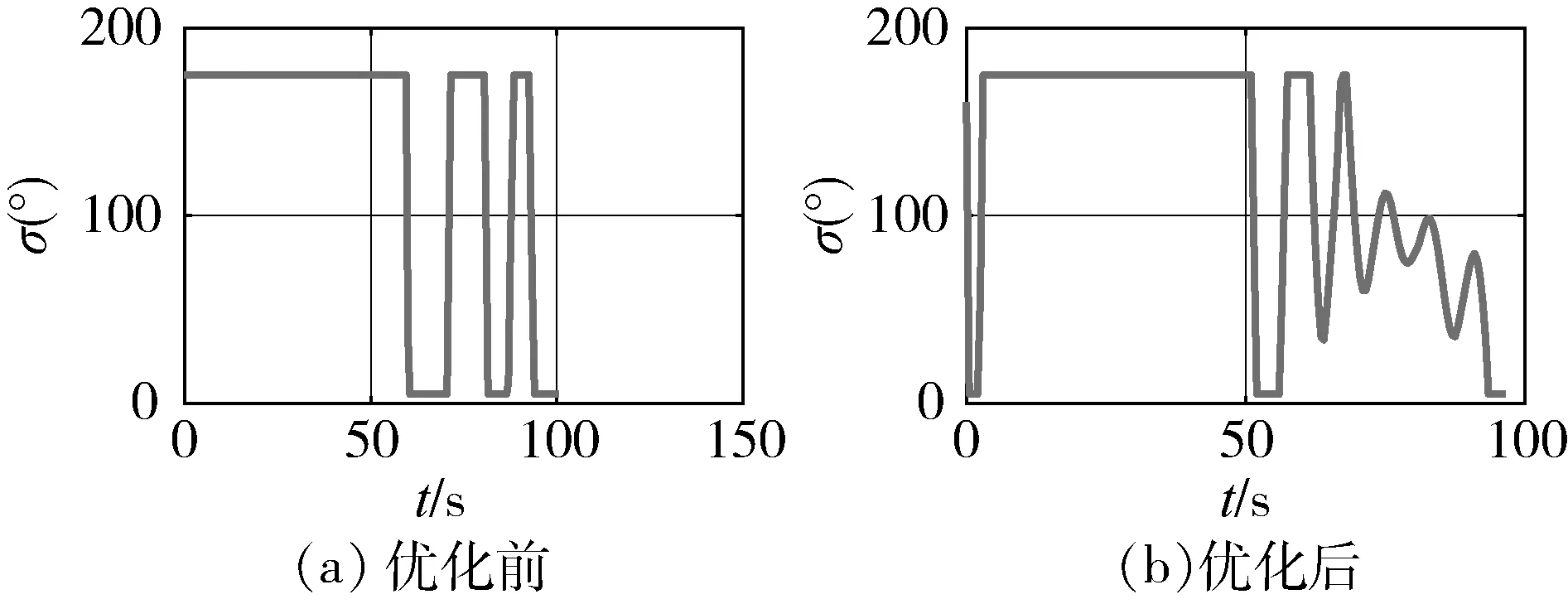
图14 倾侧角变化

由以上仿真可知，优化后的轨迹航程接近原轨迹，且与飞行器的控制能力更加匹配，优化后轨迹的跟踪精度好于优化前，再入段末端可以更好地满足倾角约束。进行了4组仿真，验证该方法的有效性，表1中列出了4组仿真案例的条件，分别是再入速度、再入段初始阻力加速度、再入段末端阻力加速度、初始航迹倾角、末端航迹倾角、航程。

表1 仿真案例初始条件

表2 中列出了4组仿真案例下轨迹优化前和优化后的跟踪效果，优化时间均在0.3s内，有3个指标，分别是最大阻力加速度偏差、末端阻力加速度偏差、末端航迹倾角偏差。

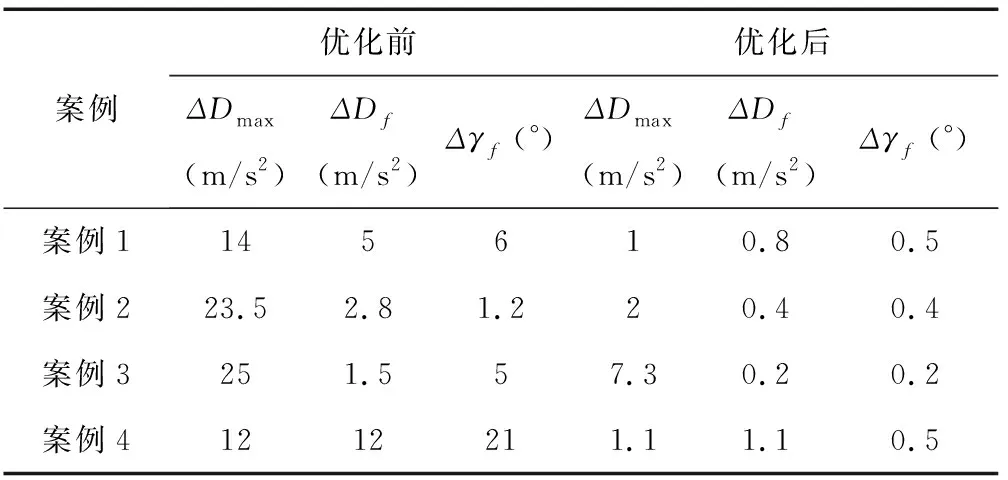
表2 优化前后仿真案例对比

根据上述结果可知，该优化方法可以在有限时间内将原轨迹修正为控制能力符合飞行器真实控制能力的轨迹，满足再入走廊和航程、航迹倾角等约束。

6 结 论

针对飞行器再入段轨迹规划问题，本文提出了一种基于椭球近似解析法的再入轨迹优化算法。经仿真，该方法可以较好地满足再入倾角约束和控制能力约束等轨迹约束，运算速率快，有一定应用潜力。