基于最小熵约束的可解释卷积神经网络
石晓荣 倪 亮 王 健 郭宇航
北京控制与电子技术研究所,北京 100038
0 引 言
导弹探测直接影响导弹打击目标的成功率。导弹武器系统上的光学探测方法必须具备高可靠性,才能保障导弹武器的成功打击。卷积神经网络近年来在图像识别领域取得了较大突破,将卷积神经网络应用于导弹武器系统有望提升目标探测打击的成功率,提高武器装备作战效能。但是卷积神经网络属于“黑盒模型”,在可靠性上不能保证,难以直接应用于导弹武器系统。
当前卷积神经网络(CNN)的解释性方面的研究从思路方面可分为2类:1)通过将输出的结果映射到输入空间,来理解CNN的决策过程,获取对于决策起到关键性作用的输入区域;2)对CNN的中间层进行研究,了解CNN内部本身的解释方式,通过中间层的一般规律解释模型,不必与输入之间存在特定的联系。
在第1个方向中,开创性的工作之一就是 Selvaraju等人提出的Grad-cam方法[1],使用了Deconvnet,该网络通过输入一个选定层的特征图,重建出最大的激活单元,通过该方法找出对于该激活单元贡献度最大的图像区域。Olah等人[2]提出了一套工具箱,用于预训练模型中卷积层编码信息的可视化。LIME[3]选择了一种更简单的处理方式,通过线性模型在样本局部对原模型进行拟合,分析对样本分类贡献度最大的图像区域,从而给出模型的解释。Zhang等人[4]提出通过图结构来描述各卷积层之间的关系,解释层级之间的语义信息。
在第2类方法中,主要的开创性工作之一是Mahendran等人[5]提出根据给出的CNN的中间层,对原图进行重构,获得CNN中每个类的理想样本,通过梯度的方式从中间层生成了能让分类分数最高的输入样本。Deep Generator Network[6]思路类似,通过给定的神经元,生成最具代表性的样本。Network dissection[7]为了量化CNN隐层的可解释性,将大量的图片输入网络模型,挑选出中间层激活程度最高的图片进行分析,将每个神经元当作一个检测单元,或进一步作为语义分割单元。
另一方面,一些工作研究当前解释方法的合理性。Sundararajan等人提出,当前大多数解释方法违背了2条公理:灵敏度和实现不变性。针对这2条公理,他们提出integrated gradients方法用于解释模型特征之间的相关性[8]。Kindermans等人同样也在该方面有相关研究:他们分析了当前用于解释多层神经网络的方法,如DeConvNet[9]、Guided BackProp[10]和LRP[7]等,发现这些方法在理论上的不合理性,并提出了2种理论上更合理的用于解释神经网络的方法——PatternNet和Pattern Attribution[11]。
目前CNN解释性方面主要的工作围绕解释常规的CNN模型的工作方式,由于CNN模型过于复杂,往往无法得到理想的解释效果[12-14]。也有一些设计本身具备可解释性的卷积神经网络,譬如Gabor卷积核[15],但是往往得到的识别模型性能损失较大。本文设计一种具有高可解释性的卷积神经网络,同时保证识别模型的性能不会有较大损失。本文利用最小熵约束,通过可解释特征的评分来对识别模型给出解释,模型有较高可解释性,并且保证了模型的识别性能。
1 提出的方法
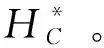
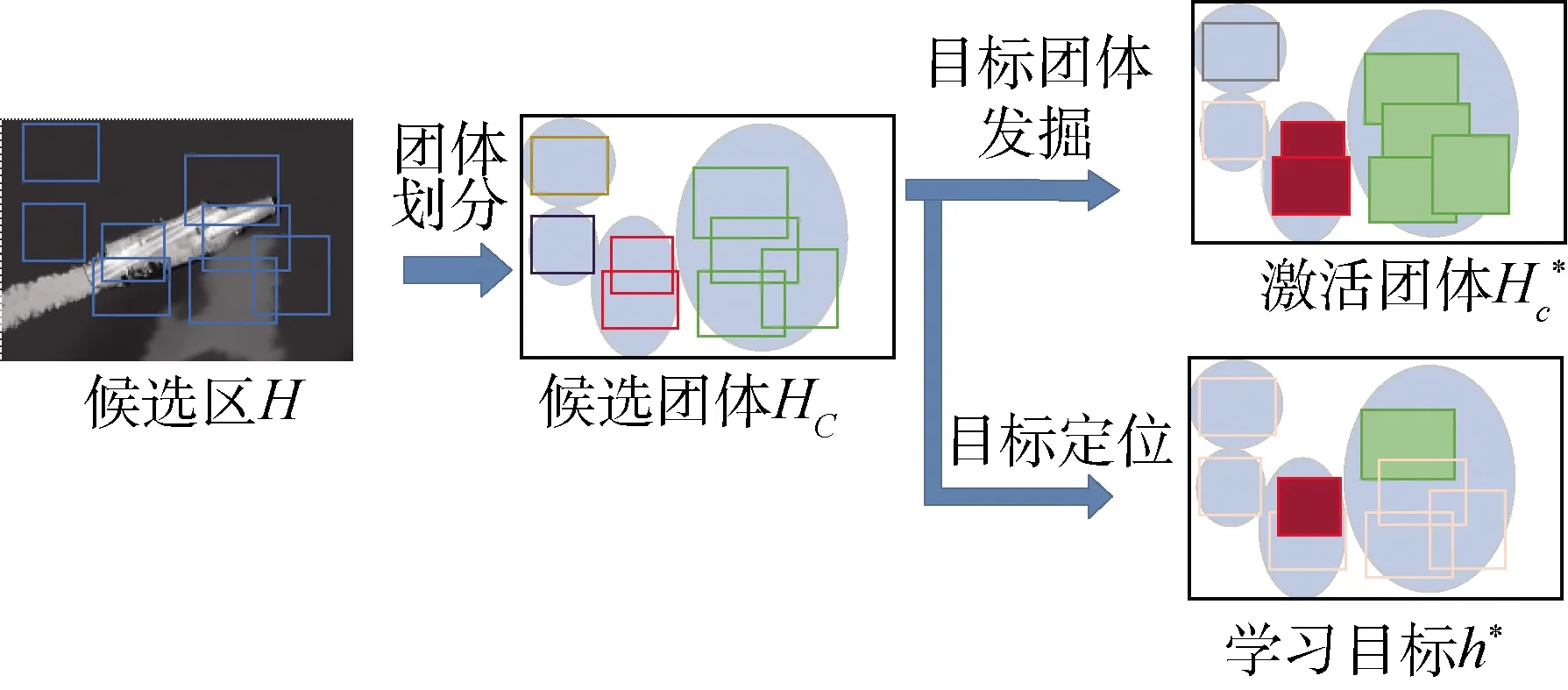
图1 整体方法思路
本文提出的网络模型,如图2所示。h表示一个目标候选区,是一个隐变量。θ表示网络参数。根据目标团体与目标的位置,联合图像标签,基于全局最小熵与局部最小熵,计算候选区分类损失和目标检测损失。目标的位置h*和网络参数θ*,可定义为:
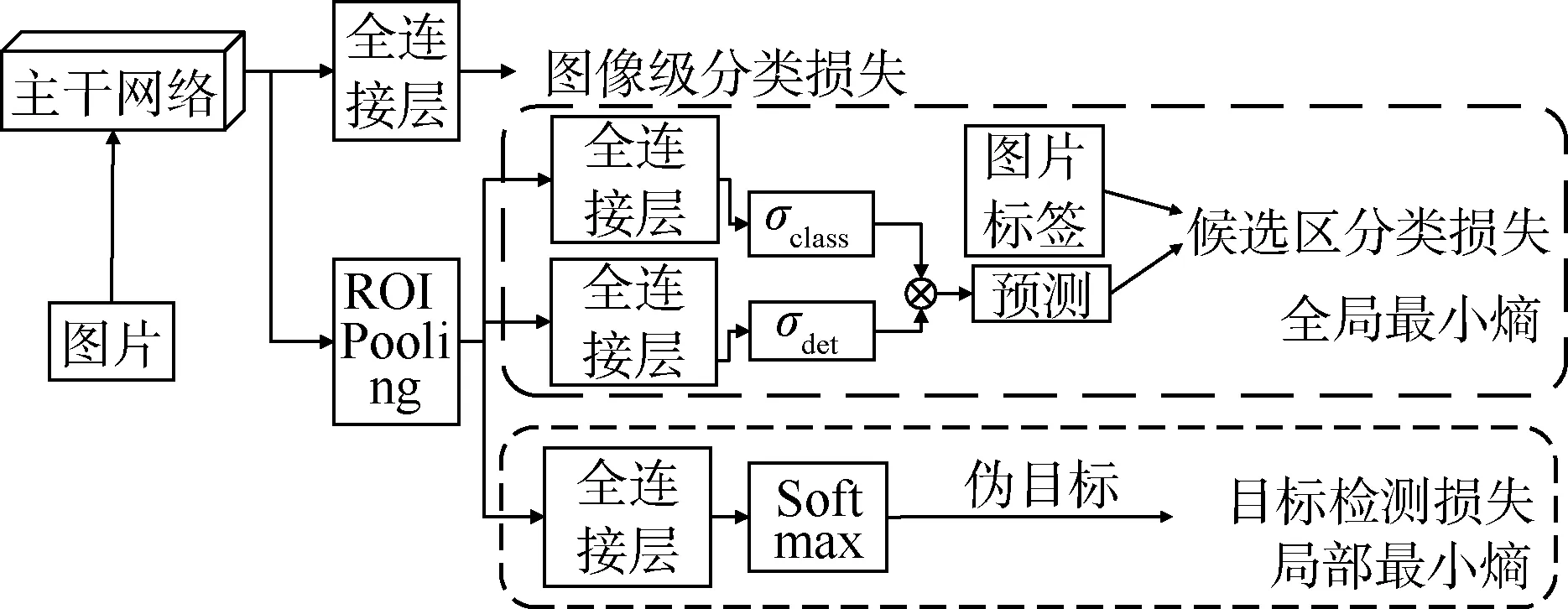
图2 模型结构
(1)
其中,x代表一幅图像,y代表x这个图像里是否包含一个目标。E(x,y)(HC,θ)、E(x,y,HC)(h,θ)分别代表全局和局部的熵模型,α是权重。
根据图像级分类损失、候选区分类损失、目标检测损失,对网络模型进行训练。本方法模型提取的特征图,目标区域与背景区域有较大差异,从而模型具有较高的可解释性。
1.1 候选团体划分
对输入图片使用ROI提取方法,获得大量的目标候选区域,其中有些候选区域表示目标,有些候选区域表示噪声,对候选区域进行聚类划分,有助于可解释网络的设计。
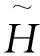
候选区团体可通过以下公式来表示:
(2)
C是候选区团体的数量(划分团体的过程相当于一个聚类过程)。为了便于划分,根据候选区的目标分数排序,然后按以下2个步骤进行迭代: 1)选择得分最高但是还未属于任何一个团体的候选区组成一个新的团体; 2)将与待观察的团体中的任何一个候选区的重合面积超过一定阈值的候选区放入待观察的团体里面去。
1.2 全局最小熵约束
在训练过程中,要求这些团体以最小的随机性进化。同时,还需要发现那些包含目标和目标部分区域的有区别的团体。这些团体可以通过激活真正的目标部分来微调网络参数。为此,定义了一个全局最小熵模型:
(3)
p(y,HC;θ)是一个类别概率,它是根据团体HC的目标分数s(y,HC;θ)定义的:
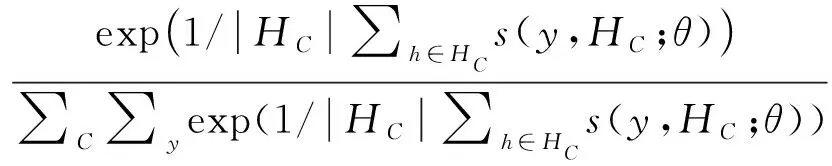
(4)
|HC|可以用来计算一个团体中候选区的数量。s(y,HC;θ)是目标团体分支中的最后一个全连接层输出的候选区的分数。为了确保被发现的团体能够最好地从图像中区分出,我们进一步引进一个与分类相关的权重ωHC。基于候选区的目标类别概率与其图像类别概率相关的知识,可定义全局最小熵为:
(5)

利用上述定义,我们在网络顶部实现了一个目标团体分支,如图2所示,并定义了一个学习网络参数的损失函数:
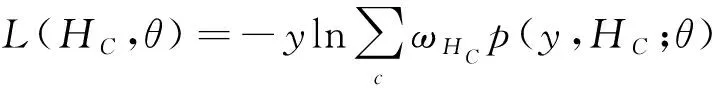
(6)
对数损失,即对数似然损失,是在概率估计上定义的。可用于评估分类器的概率输出。对于二分类问题,设y∈{0,1}且p=Pr(y=1),则对每个样本的对数损失为:
Lln(y,p)=-lnPr(y|p)
=-(yln(p)+(1-y)ln(1-p))
(7)
对于有目标图片,第2项为0,只有全局最小熵项优化。对于没有目标图片,第1项为0,第2项(图像分类损失)优化。(从公式看,y=0时,loss的目标也是让p最小,因为p代表一个候选区是某个类的概率,而当y≠0时,p代表不是某个类的概率)
1.3 局部最小熵约束
由全局最小熵模型发掘的团体可以使目标定位有良好的初始化,但同时也包含了随机误报,例如目标的部分区域和/或一些带有背景的部分的局部目标。这由目标团体的学习目标导致,该学习目标用候选区区分有目标图像和没有目标的图像,而没有考虑如何精确地定位对象。所以提出一个局部的最小熵定位模型,用于精确定位目标。
(8)
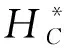
(9)
根据经验通常让α=0.6。
根据定义的伪目标和难负目标,目标检测器的损失函数被定义为:
Ll=-lnf(h*,θ)
(10)
其中f(h*,θ)表示在目标定位分支当中目标检测器的全连接层以及softmax层。
2 仿真校验
本次实验数据集选择为视觉领域常用数据集PASCAL VOC 2007。本实验中采用了VGG16作为模型主干网络,该模型用于对图片分类,通过深度堆积的卷积层,对图片进行特征提取,再通过全连接层完成对图片的分类。
另一方面,通过selective search[16]方法筛选出大量的候选区,再通过ROI Pooling[17]方法将框选出来的特征图转化为固定的尺寸,送入后续的全连接结构计算。按照上面提到的方法,获得的特征图送入2个分支:一个为全局的最小熵模型,将处理后的候选区送入2个全连接层,第1个全连接层预估每个候选区的类别概率,即判断当前区域内包含物体的可能性,再在类别维度上进行softmax处理,将其转化为概率值;另一个分支用于预测每个候选区内是否包含物体,获得2个分支之后对其进行元素级别相乘,最终获得的分值同时包含了物体的定位信息以及分类信息。再结合图片的标签计算交叉熵损失函数。
在局部最小熵的函数中,通过全局熵模型获得的分值,定义“伪目标”的标签,再根据该标签训练局部最小熵模型。
评测模型的分类性能,具体评测结果见表1。

表1 模型各类别分类准确率
文中使用的VGG16初始模型通过在ImageNet上预训练完成后获得,原VGG16模型在ImageNet上完成预训练之后,在PASCAL VOC 2007上fine-tune后的分类结果为0.869。本文提出的方法得到的准确率为85%,虽有略微下降,但在可接受范围之内。
在导弹武器系统对海打击的应用中,舰船目标的探测识别起到至关重要的作用。使用本文提出的可解释卷积神经网络,在光学舰船仿真图像上训练模型。该模型在光学舰船仿真图像上测试,舰船目标的识别率为95.2%。
在导弹对海打击应用中,仿真舰船样例如图3所示,可解释识别模型在给出分类预测的同时,还会给出图片中各个区域对识别结果的贡献度,如图4所示。贡献度最高的区域为舰岛、船头部分。根据贡献度对各区域进行排序,便可以根据最小的区域获得尽可能大的分类贡献度。

图3 仿真舰船测试样例

图4 不同图片区域及对应贡献度
3 结 论
针对导弹武器系统对光学探测算法高可靠性的要求,提出一种基于最小熵约束的可解释卷积神经网络,用于设计可解释的对海光学探测的智能目标识别模型,为卷积神经网络模型在导弹武器系统上的应用创造了条件。用传统方法(连通域检测、边缘检测等)找到图片中存在的可解释特征,用模型对可解释特征进行评分、聚类,并通过这些特征对原模型训练提供约束,在最终预测的同时,用评分解释模型。实验验证表明,基于最小熵约束模型的可解释网络在对分类性能影响程度不大的情况下(使用VGG16分类网络在PASCAL VOC2007数据集上分类准确率从87%下降到85%),能够给出合理的分类依据。在弹载条件下的光学舰船仿真图像上,本方法可以获得95.2%的准确率,根据不同区域的贡献度,可判断本方法具备可解释性。

