基于卷积神经网络的MEMS 传感器随机误差补偿方法

李英俊，褚文超，严利军，赵磊，周欣荣

（乌兰察布电业局，内蒙古乌兰察布 012000）

近年来，随着微型机电技术的迅速发展，传感器技术逐渐成为研究的热门。其中，MEMS 传感器技术发展迅速，它具有重量轻、消耗少、体积较小、成本低等优势，且易于大批量生产制造，使其在诸多技术领域得到广泛的应用[1-2]。但是，MEMS 传感器技术成本造价较低，使传感器结构和传感系统等方面存在不足，在工作运行过程中，会因外界干扰产生漂移等不稳定性误差，影响传感器的精准度[3-4]。

目前，综合各方面因素考虑，对传感器随机误差进行补偿建模是提高传感系统精准度的有效途径。因此，文中针对MEMS 传感器现存的随机性误差问题，引入了卷积神经网络领域相关知识，对传感器与陀螺仪在深度信号接收、信号定位等方面存在的随机性误差进行误差纠正和补偿方法研究。

1 卷积神经网络工作原理

卷积神经网络是一种包含卷积计算能力且具有深度结构的前馈神经网络，是深度学习代表算法之一[5]。卷积神经网络具有表征学习能力，能够按其阶层结构对输入信息进行平移不变分类。卷积神经网络结构主要包括5 个层面：输入层、卷积层、池化层、全连接层和输出层。其中，卷积层和池化层是最重要的两个层面[6]。每个层面具有多个特征面，特征面包含多种不同功能的神经元。卷积神经网络进行卷积的主要过程是将输入层特征面的神经元与输出层的相关特征面连接，通过相关权限对输出层对应的数据进行运算求和，并将运算结果传输到输入层。卷积神经网络基本结构如图1 所示。

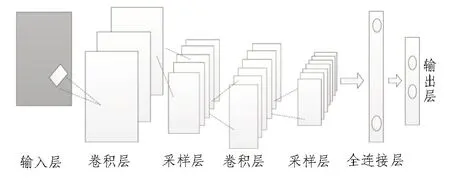
图1 卷积神经网络基本结构

文中通过分析不同行动轨迹，使实验数据具有多样性。主要实验点应分布在足够支持传感器设备正常操作运行的地区，以保证数据采集的有效性；数据采集可在能力范围内尽可能扩大传感器数据样本的采集规模，从而使实验结果更为准确[7-8]。

在原始数据的采集过程中，由于外界环境的干扰和人为因素的影响，必然会产生不同程度的干扰情况[9]，因此需要提高误差补偿模型的精准性。

环境干扰消除处理系统的操作基础模型如图2所示，根据传感器目标的位置、传感器信号发射速度和方位建设一个理想坐标系；通过具体的传感器信号数据接收，确定目标实际方位与传感器所在位置的方位关系，建立实际坐标系。用运算公式得到理想坐标系中的传感器载体的重力、速度和加速度数据，与实际数据对比，能够得到不同的数据差异，即为实际传感器受到的环境干扰数据[10]。之后，采用声波过滤器过滤掉传感器采集信号过程中其他声波的干扰，即可得到相对完整环境下的传感器信号的采集数据[11-12]。

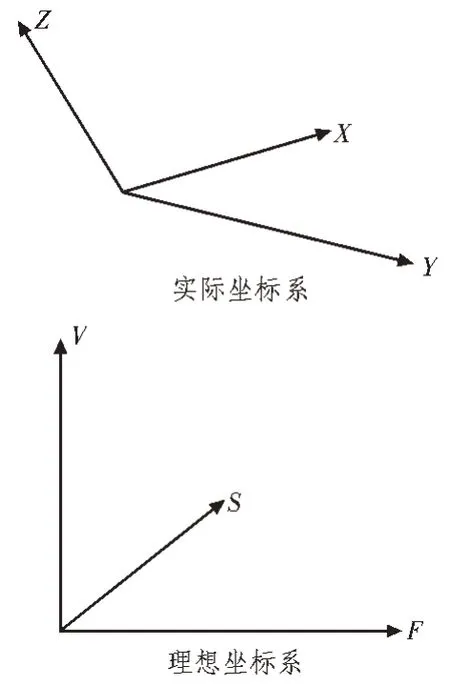
图2 干扰消除系统操作基础模型

2 MEMS传感器随机误差补偿方法

2.1 MEMS传感器随机误差类型

运用卷积神经网络对MEMS 传感器随机误差问题构建补偿模型，根据误差表现形式，MEMS 的误差大致可分为4 种类型。

1）MEMS 传感器温度漂移误差：指传感器中加速度计量仪和陀螺仪受温度差异的影响导致的误差。温度信息可在系统中央温度控制中心获取，通过温度传感器向外传输，对陀螺仪运行频率产生影响。

2）MEMS 加速度计量指标数值非线性误差：标度数值会在传感器各运行阶段发生不同变化，在安装过程中会产生误差，标度因数通过离心机的运行再次变化。离心机一般不配备温度控制仪器，导致传感器自体发热且无法散热。

3）MEMS 陀螺仪标度数值非线性误差：这种误差和第二种误差类型相似，受到温度影响，传感器的陀螺仪运行不稳定。对此，可将复杂测量数据进行筛选简化，减少系统处理内容的数量，减轻传感器发热程度。

4）加速度测量仪的向心度误差和陀螺仪加速度反应误差：加速度测量仪会在运行中受到离心力和向心力等力的作用，导致测量结果与真实数据有一定出入。这种情况可针对加速度测量仪的结构进行改装设计，削弱外力对测量结果的影响；陀螺仪在加速过程中产生的误差，也可结合离心机进行二次运算，对误差进行直接补偿，从而获得较为准确的测量结果[13]。

2.2 误差整体标定方法

为了对MEMS 传感器随机误差进行精准的补偿建模，要在模型设计之前对传感器进行初步筛选。在基础条件下，运用卷积神经网络技术对每个传感器精准度、测量范围、受环境影响大小等因素进行测量标定。文中设计了MEMS 整体标定方法，根据所有样本传感器的基本特征，设计完整的测量程序，对所有MEMS 传感器同时进行标定，省去了对每个传感器单独进行测量的步骤，能够一次性得到所有传感器每一项指标的误差数据。MEMS 传感器整体标定流程如图3 所示。

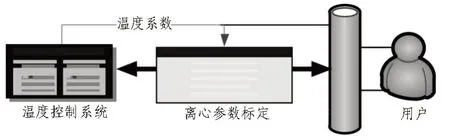
图3 MEMS传感器整体标定流程

首先检查温度控制中心，标定设置好传感器温度变化的范围，然后在既定温度范围内开启传感器，获得不同温度下加速度测量仪和陀螺仪的标度数值、耦合误差和漂移误差等具体系数。整体标定的方法不仅缩短了获取误差数据的过程与时间，而且测量准确程度也有所提高，相比于传统的标定方法更加高效准确[14-15]。

2.3 随机误差补偿方法

根据MEMS 温度标定和离心机标定获取到的参数，进行温度和离心角度差异的补偿；再根据陀螺仪加速度矩阵运算程序，得到传感器加速度测量仪和陀螺仪的参数，对传感器运行速度和旋转速率进行误差补偿；将运算所得具体数据代入到各部分的标定公式中，能够得到正常状态下加速度的速率输出和运行轨迹[16]。

在MEMS 传感器磁场定位解算中，需要通过卷积神经网络对传感器系统定位程序进行解算，解算过程如图4 所示。

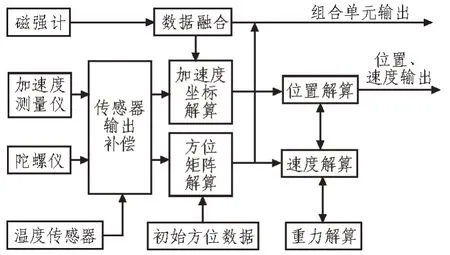
图4 MEMS传感器定位解算过程

MEMS 传感器通过标定得到各项参数，对参数运算后得到温度控制器加速度测量仪和陀螺仪的输出运行速率等方面的准确数值，进而得到误差补偿后的传感器加速度和角速率的相关信息。结合传感器磁场进行输出横向角速率的计算，通过导航仪的配合得到目标参数的坐标数据，通过四元数解算方法得到磁场传感器原始状态下的初始数据。通过对初始方位数据的运算，对受到漂移误差影响的MEMS 传感器进行输出误差修正，四元数解算算法如下：

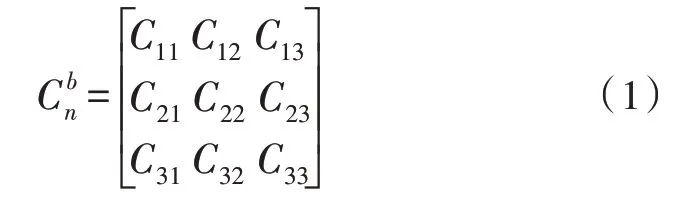
根据矩阵运算得到四元数初始数据为：

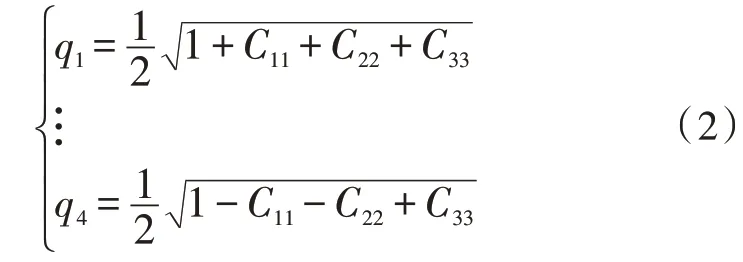
依据式（2）运算得到的四元数的初始数据，再进行四元数解算公式运算：

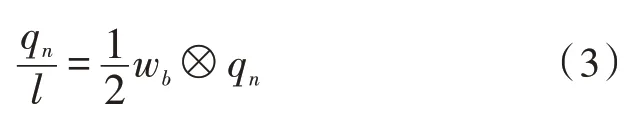
式（3）中，qn表示初始方位四元数，wb表示传感器加速度运行的角速率。

根据四元数运算方程进行求解，得到初始状态下传感器加速度与角速率的理想数据，再与实际测量标定的数据进行对比，得出传感器随机误差产生的原因和大致规律。

结合温度系统、加速度测量仪、陀螺仪、磁场定位导航等各方面传感器误差补偿方法，可较为准确地标定出传感器在异常温度、高加速度、高角速率等问题影响下产生的误差数据。

3 实验研究

为了验证卷积神经网络对MEMS 传感器随机误差补偿方法的有效性，文中针对MEMS 传感器随机误差补偿方法进行了对比实验，分别对深度信念网络、循环神经网络和卷积神经网络对传感器随机误差补偿方法各方面的性能进行分析测试。

首先针对传感器信号采集范围内受环境影响产生的误差，文中采用3 种神经网络误差补偿模型对补偿误差进行实验，实验数据如图5 所示。

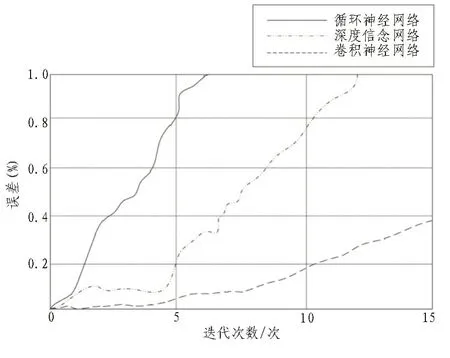
图5 不同方法补偿模型误差对比

经过对比实验分析，基于卷积神经网络的传感器误差补偿模型比传统的误差补偿模型效果更好，且误差最低，而基于神经网络的传感器误差补偿模型和基于循环神经网络的误差补偿始终高于所提方法。由此可见，在受到外部环境影响的情况下，卷积神经网络误差补偿模型对随机误差的补偿效果更好，误差补偿性能更优。

为了验证所提方法的科学有效性，实验分析了3种方法的补偿效果，如图6 所示。

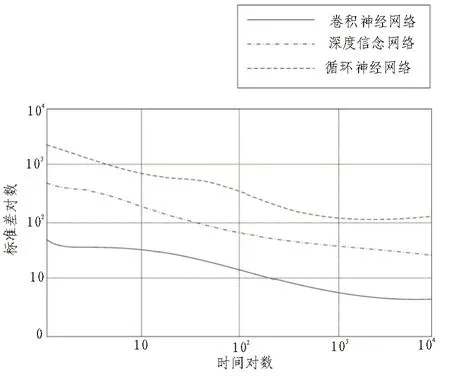
图6 补偿模型漂移误差补偿效果对比

图6为基于3种神经网络的传感器误差补偿模型对漂移误差补偿的效果对比。可见相对于传统的误差补偿模型，提出的基于卷积神经网络MEMS传感器误差补偿模型对漂移误差补偿结果更稳定，数据差异更小，对漂移和随机游走误差的补偿性能更强。

针对传感器加速度测量仪和陀螺仪容易产生的加速度和角速率误差，文中将3 种误差补偿模型置于同一环境中，采用相同传感器配置进行了对比实验，实验数据如图7、8 所示。

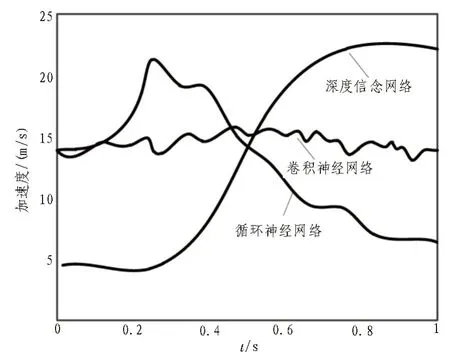
图7 补偿模型加速度误差补偿效果对比

从图7、8 中可以看出，对于MEMS 传感器的随机误差，相比于传统的误差补偿模型，基于卷积神经网络的误差补偿模型对传感器加速度和角速率的误差补偿效果更好。如图7 所示，基于卷积神经网络误差补偿后，加速度的变化更平稳，随着时间推移变化程度起伏越来越小。

图8 中，传感器角速率有明显变化，对应着实验中运行轨迹的变化，而传统补偿模型角速率误差补偿后的数值仍趋近于0。由此可见，提出的基于卷积神经网络的MEMS 传感器随机误差补偿模型更为优秀，误差补偿效果更好。

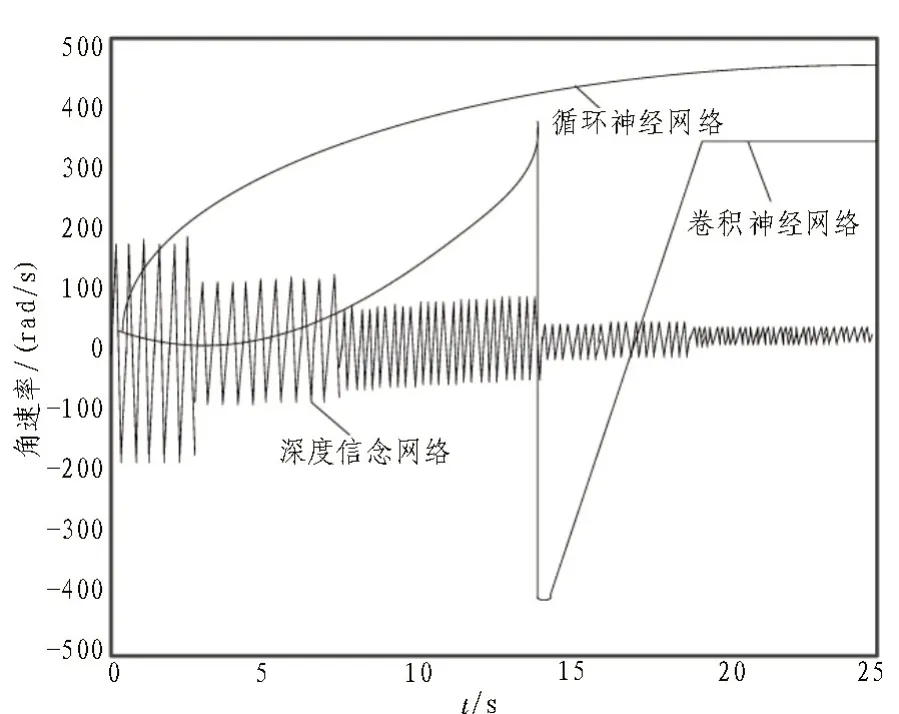
图8 补偿模型角速率误差补偿效果对比

4 结束语

文中主要针对MEMS 传感器随机误差对测量工作产生的影响，以及误差产生的各部分数据对比，提出了基于卷积神经网络的随机误差补偿模型，并与传统的误差补偿模型进行对比实验。实验结果表明，基于卷积神经网络的误差补偿方法能够更精准、更稳定地对传感器误差进行补偿，而且效率更高，所需成本更小，误差补偿的效果更好。该研究成果对相关领域的传感器误差补偿方法研究提供了宝贵经验，对日后的传感器误差补偿技术研究起到一定的指导作用。