基于梯度下降算法的飞行器姿态解算

高 怡，李东航，郭 飘

（西安石油大学电子工程学院，陕西西安 710065）

获得精确的实时飞行姿态是实现飞行器控制的前提条件。对于传统的惯性测量单元(Inertial Measurement Unit,IMU)，陀螺仪与加速度计的测量性能各有利弊：加速度计在实际使用中的动态性能很差，物体高速运动下所测的数据有很大的延迟；陀螺仪可以有效处理高速运动下的动态数据，可对加速度计的数据进行补偿。但仅凭加速度计和陀螺仪的数据融合不能很好地求解偏航角的值，还需要引入磁力计来修正。

针对上述问题，国内外学者提出了多种姿态解算方法。常见的方法有互补滤波(Complementary Filtering,CF)[1]法、扩展卡尔曼滤波(Extended Kalman Filter,EKF)法[2-3]、梯度下降(Gradient Descent)法[4-6]等。

文献[1]使用互补滤波算法，针对陀螺仪在低频段的动态响应特性较差，使用高通滤波器抑制噪声；加速度计、磁力计在高频段的动态响应特性较差，使用低通滤波器抑制噪声，从而实现传感器动态响应特性的互补。该方法实用性强，但不适用于高精度要求的导航系统中。文献[2]中基于扩展卡尔曼滤波算法提出了一种改进算法，解算偏航角时加入一个方差矩阵，可以自适应改变卡尔曼增益值，从而减小了磁场对偏航角解算的影响。文献[3]提出了高阶线性互补滤波与扩展卡尔曼滤波相结合的融合算法，明显地去除了噪声并抑制了姿态角的漂移。EKF 算法虽然能求解出高精确度的姿态，但该算法计算量很大，对处理器的运算速度和精度要求很高，不适用于低成本飞行器应用。文献[4]首次将梯度下降(Gradient Descent,GD)法应用在了姿态解算领域中。GD 算法具有可快速跟随高速运动中的姿态变化、收敛速度快等优点，适用于低成本飞行器的研究。

1 飞行器姿态描述

1.1 建立坐标系

选用地理坐标系东、北、天（O-ENU）作为参考坐标系（Reference Coordinate System）。载体坐标系（Carrier Coordinate System）X轴为载体平面向右方向，Y轴为机头所对的方向，Z轴与载体横截面垂直向上，构成坐标系O-XYZ，如图1 所示。

图1 载体坐标系

1.2 姿态角

载体的姿态角偏航角、滚转角和俯仰角[7-8]——载体绕Z轴旋转，载体Y轴在参考坐标系E-O-N平面上的投影与参考坐标系N轴之间的夹角称为偏航角(Yaw)，用字母ψ表示；载体绕Y轴旋转，载体Z轴在参考坐标系E-O-U平面上的投影与参考坐标系U轴之间的夹角称为滚转角(Roll)，用字母γ表示。载体绕X轴旋转，载体Y轴在参考坐标系U-O-N平面上的投影与参考坐标系N轴的夹角称为俯仰角(Pitch)，用字母θ表示。

1.3 坐标变换

设坐标系O-X0Y0Z0中有一向量P，P在该坐标系中的投影为，令坐标系绕OZ0轴转动一个角度α，得到新坐标系O-X1Y1Z1，P在新坐标系中的投影为，坐标变换关系如图2所示。

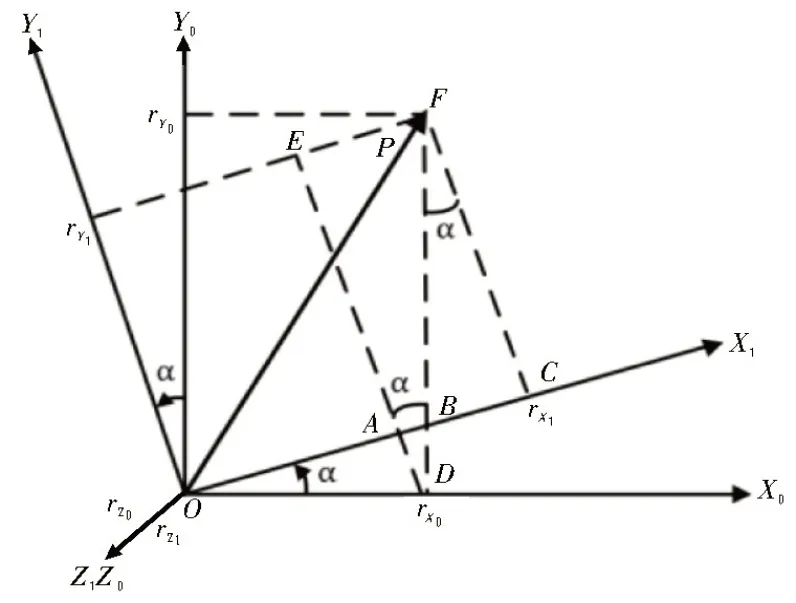
图2 坐标变换关系示意图

由图2 可得如下关系：

1.4 方向余弦姿态矩阵

两个坐标系之间的位置关系都可以看作是有限次基本旋转的组合，坐标变换矩阵等于每次基本旋转矩阵的左乘积[9]。

若规定坐标旋转次序为Z→Y→X，旋转矩阵由3 个基本旋转矩阵依次左乘求得：

1.5 四元数姿态矩阵

设矢量P在两个坐标系中的投影为R=x1i+y1j+z1k,R′=x2i+y2j+z2k，设四元数为Λ=λ0+λ1i+λ2j+λ3k。

两坐标系之间的旋转关系可以由R′=Λ ⊗R⊗ΛR′得到[10]（Λ′为共轭四元数），整理得四元数姿态矩阵为：

2 数据融合与姿态解算

飞行器的惯性测量单元(Inertial Measurement Unit,IMU)通常搭载了加速度传感器与陀螺仪来测量实时姿态数据，并且使用磁力计来修正偏航角的值。

梯度下降算法的基本思想如下[11-12]：首先，通过陀螺仪的角速度初步计算传感器方向偏移；然后通过对重力加速度和地磁两个恒定量在传感器坐标系下的投影计算传感器的方向偏移；最后通过梯度下降法对这两个偏移量进行数据融合，从而得到一个更加准确的解算结果。

经典梯度下降法公式为[13]：

其中，∇F(xn)是该函数在xn点处的梯度，μt为步长。

用加速度计的数据表征四元数矩阵的误差，则误差函数为：

求导，得到矩阵：

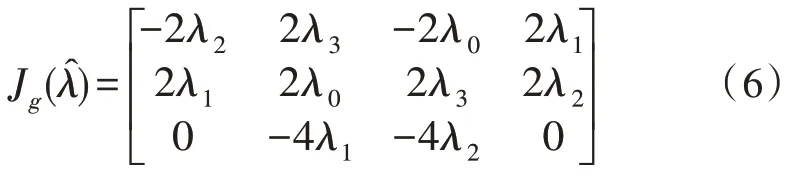
根据梯度计算公式有：

假设目标姿态为λ∇,t，由梯度下降法公式有：

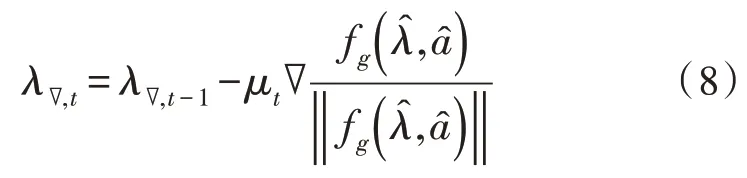
由于加速度计在实际使用中的动态性能很差，在物体高速运动下所测的数据会有很大的延迟，而在惯性导航中，陀螺仪能有效处理高速运动下的动态数据[14]。考虑到二者特点互补，需要对它们的数据进行融合。

设基于陀螺仪的四元数微分方程求解到的姿态为λω,t，则融合后的四元数为：

式中，0 ≤α≤1。等号右边由两部分组成：一是利用梯度下降法得到的低速姿态四元数λ∇,t，二是基于陀螺仪的微分方程求解到的高速姿态四元数λω,t[15]。

α的取值应该使λ∇,t的收敛速度等于λω,t的收敛速度β：

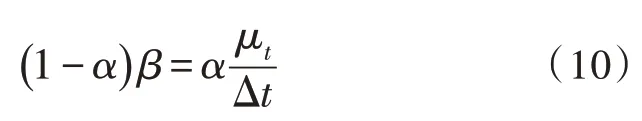
由于α的值一般都很大，故式（8）有近似表达式，如下：

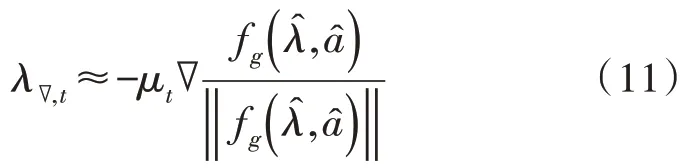
将所有表达式代入式（9）中，可得最终融合算法公式，如下：

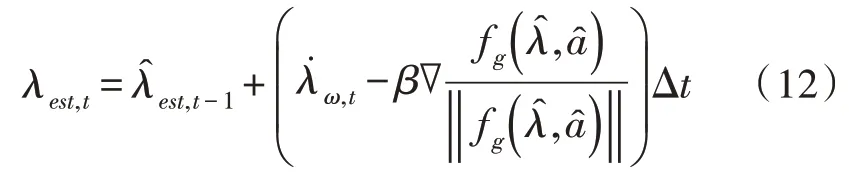
加速度计与磁力计的误差函数可以写成一个6行1 列的矩阵，对其求导得：

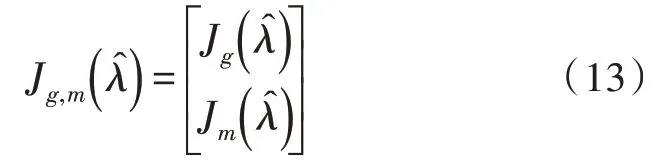
代入梯度公式可得：

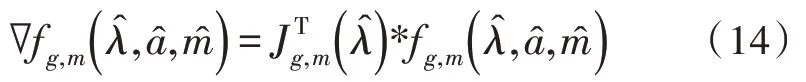
后续工作与加速度计和陀螺仪的融合过程类似，最终也可得加速度计和磁力计的融合算法公式。

3 试验与分析

姿态航向参考系统(Attitude and Heading Reference System,AHRS)是一种基于微机电系统(Micro Electro-Mechanical Systems,MEMS)技术的高性能、低成本捷联惯导测量装置[16]。为验证算法的可行性，设定AHRS 设备分别绕Z、X、Y轴从0°旋转至+90°，再旋转至-90°，将3 次旋转过程采集到的传感器数据进行降噪处理，输出的9 组传感器数据及采样时间数据以.mat 文件的形式存储。经过程序解算，该AHRS 3个预定轨迹的解算结果如图3所示。

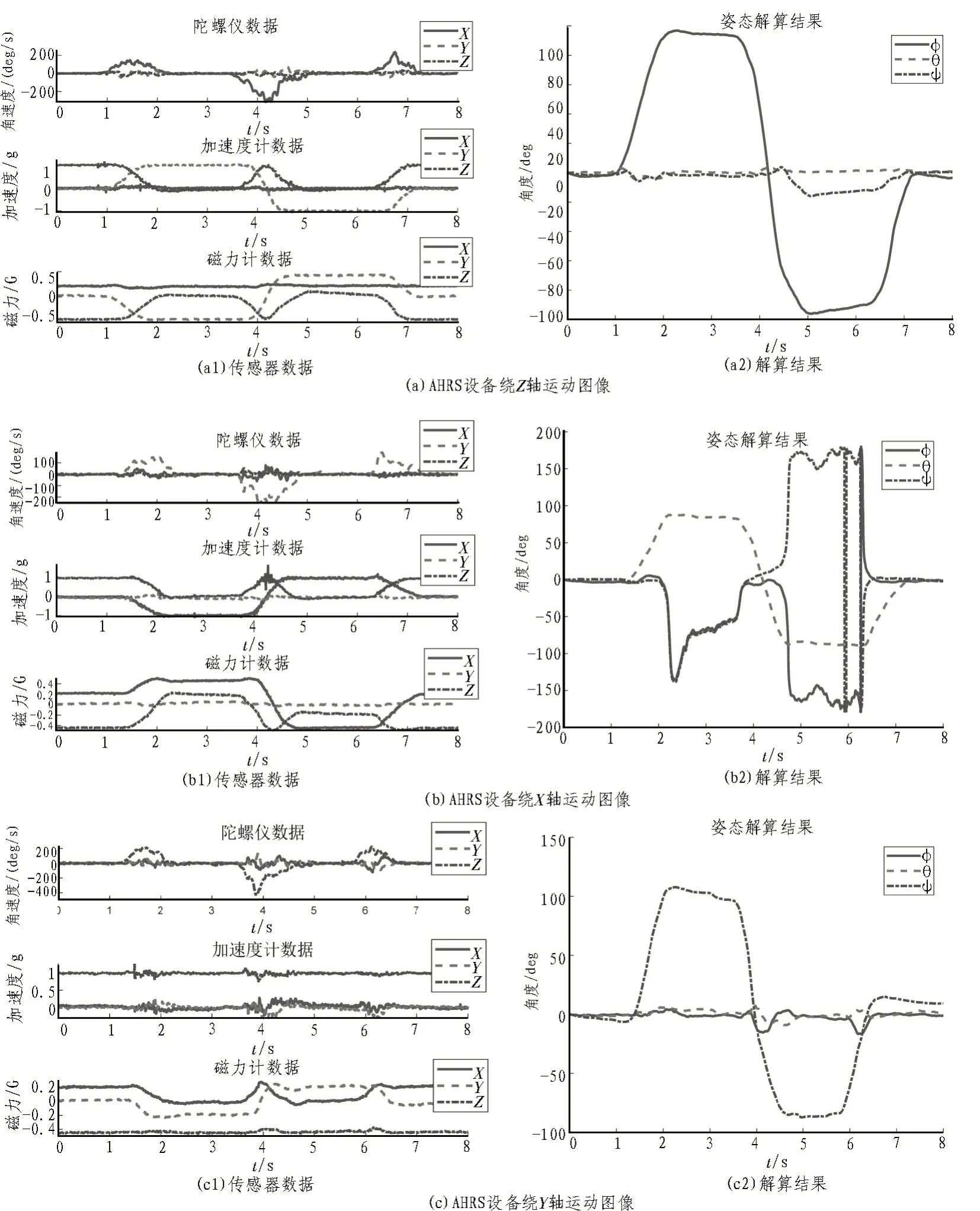
图3 试验解算曲线

图3(b2)中，当俯仰角在±90°附近时，其他两个角的数值是无效的，这是由于“万向节锁”现象造成的——当俯仰角等于±90°时，滚转和偏航两个旋转轴对于飞行器的旋转效果相同，从而丢失了偏航效果[17]。但由于使用四元数法解算姿态，相比于欧拉角法，不会出现方程奇异解的情形，俯仰角依然解算成功。

由图3(a2)、(b2)、(c2)可以看出，当AHRS 设备分别绕Z、X、Y轴从0°旋转至+90°，再旋转至-90°时，姿态解算结果曲线与设备预定运动情况完全符合，由此说明了该姿态解算程序的可行性。

4 结论

在飞行器姿态解算中，鉴于各传感器测量特性的利弊，需要对多个传感器的数据进行融合，使用梯度下降算法可以使加速度计测得的低速姿态信息与陀螺仪数据求解到的高速姿态相融合，并且还能与磁力计的数据融合来修正偏航角的解算值。令AHRS 设备分别绕Z、X、Y轴旋转，通过算法程序解算，得出了与该设备预设旋转情形完全相同的姿态角结果，验证了算法的可行性。

该解算算法具有在较慢速运动中精度高、可快速跟随高速运动中的姿态变化、无需获知当地地磁倾角、收敛速度快等优点，有一定的工程应用价值，适用于低成本飞行器姿态测量与控制的研究。下一步工作考虑如何自适应地选择步长μt，从而在飞行器机动状态下获得更加精确的姿态。